一种行星车视觉导航系统的立体校正算法

王怀超，张学全，李海丰

(1.中国民航大学中国民航信息技术科研基地，天津300300;2.中国科学院国家空间科学中心，北京100190)

一种行星车视觉导航系统的立体校正算法

王怀超1，张学全2，李海丰1

(1.中国民航大学中国民航信息技术科研基地，天津300300;2.中国科学院国家空间科学中心，北京100190)

针对行星车软着陆过程中，视觉导航系统参数变化后星面再标定难度大的问题，在传统立体校正算法基础上提出了一种适用于行星车视觉导航的弱标定立体校正算法。算法利用地面标定结果和对应匹配点进行优化计算，约束校正矩阵形式，保证了校正结果为以光心为投影点的单应变换，并进一步简化参数，降低计算复杂度。在理论上证明了算法的正确性，实验验证了算法的有效性。实验结果表明，算法校正结果与已知相机内、外参数的欧几里德校正方法性能相当，校正误差和校正畸变均较小，满足行星车视觉导航系统要求。

行星车;视觉导航;立体校正;基础矩阵;极线几何

0 引 言

基于视觉的环境感知技术属于被动感知，与主动感知技术相比具有功耗小、可一次性捕获整幅画面且无需机械扫描部件等优点，因而广泛地应用于行星车(Planetary rover，PR)中，特别是基于双目视觉的环境感知技术，如美国好奇号火星车探测器［1］、我国月兔号月球车［2－3］。通过处理视觉信息，行星车可以获得对周围环境的感知进而实现路径规划。环境感知能力对行星车的生存和安全有着非同寻常的意义。其中，双目立体匹配的精度是影响行星车环境感知能力的重要因素，作为立体匹配重要步骤的立体校正通过对两幅图像各进行一次单应变换，使立体匹配问题从二维的搜索问题变为在一维扫描线上的搜索问题，大大减少冗余计算，加快匹配速度，也降低了误匹配出现的可能性。

针对双目视觉系统的立体校正，现有的方法主要分为两类。第一类方法基于相机的内、外参数标定［4］的欧几里德校正方法。这种方法需要提前标定立体相机内、外参数，操作较为繁锁，但校正精度高［5－6］。对于行星车视觉导航系统，由于受到软着陆过程中的冲击、震动、温度变化等因素的影响，立体视觉系统中的相机参数会发生微小变化。如果直接利用地面的欧几里德标定结果进行三维重建，必然精度不高，并对后续的路径规划造成影响，降低行星车的星面生存能力。第二类方法基于图像本身的特性，通过图像中的特征点作为标志点，利用双目图像中对应点的极线特性，构建图像变换矩阵，将特征点的极线在极平面内保持平行，从而消除图像间的垂直视差［7－9］。此类方法都要用到复杂的非线性优化计算，不能直接应用于行星车这种计算资源有限的系统，需要在算法稳定性、速度等方面进行改进和完善。同时，这类算法往往只利用射影变换本身性质进行优化，所得到的解是不适定的，产生的结果不一定是以光心为投影点的单应变换，校正后的两图像间的基线会发生变化，在一定程度上降低后续三维重建的精度，从而降低行星车的生存能力。

本文综合应用以上两类方法的思想，针对行星车视觉系统在软着陆过程中的参数变化后星面再标定难度大的问题，设计了一种应用于精确的三维星面地形重建的弱标定立体校正算法。本算法利用地面欧几里德标定结果和对应匹配点进行优化计算，约束校正矩阵形式，并从理论上证明了所加约束的合理性，保证校正结果为以光心为投影点的单应变换和基线长度不变，进一步简化参数、降低计算复杂度，最终校正结果与已知参数的标定方法相差很小。

1 极线几何

双目视觉成像系统由两个针孔摄像机构成，如图1。三维空间点W投影到像平面R1和R2上，得到像点M1和M2(M1和M2是一对共轭点)。M2必位于由M1和两个相机的几何位置决定的某一条直线上，也就是像平面R2上对应于M1点的极线。

设m1和m2分别是对应点M1与点M2的图像齐次坐标，它们满足以下关系式［8］:式中:F称为基本矩阵。在给定m1的情况下，式(1)是一个关于m2的极线方程，即像平面R2上的极线方程，反之亦然。

两像平面(如图1)一般不共面，而若两像平面共面，则对应外极线处于同一水平线上，即在扫描线上(如图2)。图像的立体校正就是把外极线变换成扫描线的过程。基本矩阵F可分解为F=［e1］×M，M是一个包含三个参数的非奇异矩阵。两个极点e1和e2，满足Me2=e1。对于校正后的图像，极点坐标为e1=e2=［1，0，0］T，基本矩阵F变为:

2 本文算法

2.1 欧几里德校正

定义1.在已知左右相机内参数矩阵Kl、Kr和相对外参数R、t的情况下，在欧几里德空间内，利用欧几里德几何性质进行的两相机的立体校正过程，称为欧几里德校正。所求得的左右相机的立体校正矩阵Hl、Hr称为欧几里德校正矩阵。

2.2 弱标定情况下的欧几里德校正

2.2.1 优化函数

设Hl、Hr为待求的用于左右相机校正的单应矩阵，对于j对共轭对应点

可以看出等式左边只是一个代数的上的误差，并不存在任何几何信息。所以本文利用Sampson误差。矩阵可以看成是校正前左右图像间的基础矩阵，故可将Sampson误差表示成:

式中:u2=(0，0，1)。

给定j对共轭对应点，则存在关于Hl和Hr的j个非线性方程{=0}，i=1，2，…，j。则优化函数有如下形式，

使这个优化函数最小的Hl和Hr就是需要求取的投影变换矩阵。

式(5)中由于参数过多，直接优化计算量较大，而且约束较少，为保证所得的校正矩阵为欧几里德校正矩阵，减小计算复杂度，本文对如下两个小节所述的5个方面进行了优化。

2.2.2 约束校正矩阵形式

为保证行星车自主行驶安全，视觉导航系统在行星的表面三维重建过程中必须具有较高的精度，这就要求立体校正不能产生较大的次采样和过采样，这样变换后结果必须与欧几里德校正相似。如果不对Hl和Hr进行约束或只利用校正投影变换的性质进行约束，直接对式(5)进行优化，则校正结果一般会与欧几里德校正偏差较大，次采样和过采样效果明显，而且有可能改变基线长度，并不能直接用于精确三维重建。

命题1.Hl、Hr为欧几里德校正矩阵且同时Hl、Hr为左右光心的单应矩阵的充分必要条件为。其中Kol、Kor分别为左右相机校正前内参数，Knl、Knr为校正后左右虚拟相机内参数，Rl、Rr分别为左右相机校正前后像平面之间的旋转矩阵。

证.以左相机为例，先证充分性。

式中:Kol和 Knl为校正前后左相机内参数矩阵，Rol、Rnl、tol和tnl分别对应于校正前后左相机外参数中的旋转矩阵和平移向量。公式中的Qol和Qnl满足，

若校正前后均为左相机光心的单应矩阵，则，

式中:Ocl为左相机的光心坐标。这样，

将式(8)代入式(10)，得到，

同理可证。

必要性:可按照充分性的逆过程证明，略。

本文为保证在相机参数变化情况下变换后结果依然是欧几里德校正，根据命题1结果，约束变换投影矩阵Hl和Hr有如下形式:

则式(5)中的基本矩阵F可以表示成，

这样，对基本矩阵F有式(13)的约束后，对优化函数(5)进行优化所得的变换投影矩阵Hl和Hr就为欧几里德校正矩阵，次采样和过采样均较小，而且变换投影矩阵Hl和Hr为光心点的单应矩阵，保证基线长度不变。

2.2.3 简化参数和优化

由于优化函数中的所有参数均在F中，式(13)中共包括22个参数，参数过多，直接优化计算量较大，下面根据各个参数间的性质，对参数进行简化。

(1)消去内参数Knl和Knr

根据立体校正性质，得Knl=Knr，

这说明对于变换后的两相机内参数Knl和Knr，满足，则式(13)中的基本矩阵F可以简化成如下形式:

消去内参数Knl和Knr后，F中的共含有14个未知参数。

(2)减少旋转参数

绕X轴旋转α，则旋转矩阵

(3)像主点坐标不变假设

在行星车视觉导航系统中，由于相机本身是制造成一体的，所以可以假设相机的内参数在软着陆过程中是不变。本文中只假设相机内参数中相主点坐标不变，焦距可能发生变化。其中，

这样我们最终得到

其中共包括αl，αr两个内参数和α，β，φ，φ，ω五个旋转参数。

经过一系列简化后，式(13)中，F中共含有7个参数。

(4)增加约束

然而对于行星车视觉导航系统来讲，左右相机在地面上已经几乎平行放置，即外参数中的五个旋转参数都很小，但如果直接最小化优化函数(5)，但所求得的参数则有可能使校正后的图像存在较大的变形，因此为式(5)增加一个旋转角度的约束。

最终得到优化函数，

式中:所有参数均在F中，共含有7个参数。

2.2.4 求解校正矩阵

显然上述优化问题可以看成是一个非线性最小二乘问题，可以用Levenberg-Marquardt算法优化。Levenberg-Marquardt算法存在对初值较为敏感的问题，本文背景中，由于行星车在软着陆过程中参数发生微小的变化，故可以利用地面的标定结果作为Levenberg-Marquardt算法的初值，这样，很快便可以得到最优解。最后将优化的结果αl，αr两个内参数和α，β，φ，φ，ω五个旋转参数代入到式(12)中，适当选取Knl和Knr便可得到最终的立体校正矩阵。本文中选取

这样最终所求的的立体校正矩阵为:

3 实验及结果分析

在实验室内搭建双目视觉系统验证平台，如图3所示，将两台Baslar CCD相机(分辨率为1024× 1024，感光芯片为KAI－1050，像素尺寸为5.5 μm× 5.5 μm)固定在摄影基线约为20 cm的基线上，并进行了精确的标定，两相机的内参数如表1所示，相对外参数如表2所示。

表1 两相机的内参数Table 1 The intrinsic parameters of the two cameras

表2 两相机的相对外参数Table 2 The calibrated outer parameters on the earth

表3 参数变化后两相机的相对外参数Table 3 The calibrated outer parameters changed

在试验场内对双目视觉验证系统中的两相机相对位置做微小的变动，参数变化后对视觉系统进行再标定，标定结果如表3所示。以此来模拟在软着陆过程中行星车视觉导航系统的参数变化。在试验场内获取一系列图像，图像采样大小为512×512，部分图像如图4所示。按照本文算法对两图像进行立体校正，算法的初值如表1和表2所示，对于行星车来讲，初值即为地面的标定结果。图4(c)和图4(d)为对变动后的视觉系统进行再标定，然后利用标定后内外参数进行欧几里德校正的结果。图4(e)和图4(f)为利用本文算法进行校正的结果。可以看出本文算法产生的校正结果与参数变化后再标定的欧几里德校正结果基本一致，说明了本算法的有效性。

为了将本文算法与欧几里德校正在校正性能上进行定量对比分析，利用如下两个常用的衡量指标:

(1)校正误差:该项指标用于衡量校正后图像匹配点之间的垂直视差大小，该指标定义为:

(2)校正畸变:该项指标用于衡量校正算法对图像产生的变形大小，该项指标定义为:

式中:Spixel为校正后图像像素所占的面积，而SAR为校正后图像最小外接矩形的面积。

表4给出了以上两个指标针对图5的测试图像的计算结果。

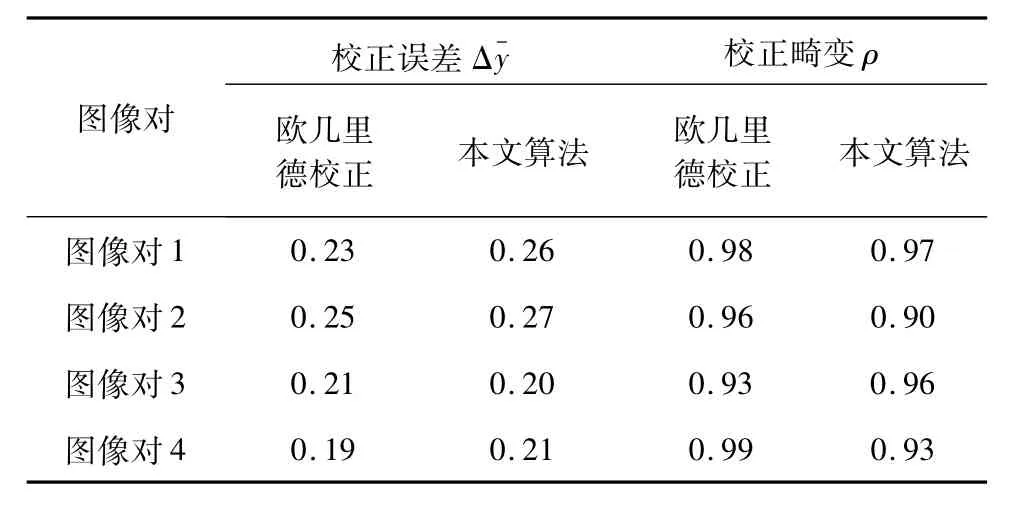
表4 本文算法与欧几里德校正结果比较Table 4 The rectification error and distortion comparison between the Euclidean rectification after re-calibration and our method

由以上比较结果可以得出结论，本文算法产生的校正结果与已知内外参数的欧几里德校正算法校正性能相当，校正误差和校正畸变均较小。由于其他弱标定系统的立体校正算法，如文献［7－11］，都不约束校正矩阵为光心点的单应矩阵，产生的结果有可能导致基线长度发生变化，并不能用于精确的三维重建，故本文并未与此类算法进行比较。

4 结 论

由以上论述和测试结果可以看出本文提出的立体校正算法具有以下特点:

(1)本文立体校正算法为弱标定系统下的立体校正算法，算法原理上不需要对双目视觉系统的全部参数进行标定。行星车视觉导航系统在软着陆过程中参数发生变化后，本文算法可完成校正。

(2)本文立体校正算法所得到的校正矩阵为光心点的单应矩阵，保证双目视觉系统的基线长度不变，可用于精确的三维重建。

(3)本文算法产生的校正结果与已知内外参数的欧几里德校正算法校正性能相当，校正误差和校正畸变均较小，满足行星车视觉系统要求。

［1］ Thomas M H，Arin M，Jack M，et al.Enabling continuous planetary rover navigation through FPGA stereo and visual odometry［C］.2012 IEEE Aerospace Conference，MT，March，2012.

［2］ Du J J，He J S，Zhu J J，et al.A method study of generating digital terrain map for lunar exploration based on the stereo vision［C］.The IEEE International Conference on Information and Automation，Shenzhen，China，June，2011.

［3］ Mao X Y，Chen J X，Xing Y，et al.Lunar rover’s vision technology for auto-navigation［C］.The 33rd Chinese Control Conference，Nanjing，China，July，2014.

［4］ 王保丰，毛晓艳，唐歌实.月球车鱼眼相机的标定方法研究［J］.宇航学报，2011，32(4):933－939.［Wang Bao-feng，Mao Xiao-yan，Tang Ge-shi.A calibration method for fish-eye camera of lunar rover［J］.Journal of Astronautics，2011，32 (4):933－939.］

［5］ Kanbara M，Okuma T，Takemura H.A stereo-scopic video seethrough augmented reality system based on real-time vision-based registration［C］. International Conference on Pattern Recognition，New Brunswick，Canada，March，2000.

［6］ Takagi A，Yamazaki S，Saito Y.Development of a stereo video see-through HMD for AR systems［C］.IEEE and ACM InternationalSymposium on Augmented Reality， Munich Germany，August，2002.

［7］ Richard I H.Theory and practice of projective rectification［J］.International Journal of Computer Vision.1999，35(2):115－127.

［8］ Loop C，Zhang Z Y.Computing rectifying homographies for stereo vision［C］.The International Conference on Computer Vision and Pattern Recognition.Collins，USA，January，1999.

［9］ Fusiello A，Trucco E，Verri A.A compact algorithm for rectification of stereo pairs［J］. Machine Vision and Applications，2000，12(1):16－22.

［10］ Andrea F，Luca I.Quasi-Euclidean uncalibrated epipolar rectification［C］.The 19th International Conference on Pattern Recognition.Tampa，USA，January，2009.

［11］ 林国余，张为公.一种无需基础矩阵的鲁棒性极线校正算法［J］.中国图象图形学报，2006，11(2):203－209.［Lin Guo-yu，ZhangWei-gong.An effectiverobustrectification method for stereo vision［J］.Journal of Image and Graphics，2006，11(2):203－209.］

通信地址:天津市东丽区中国民航大学南院南教 4－320 (300300)

电话:(022)24092488

E-mail:junkda@163.com

(编辑:张宇平)

A Stereo Rectification Algorithm for Planetary Rover Visual Navigation System

WANG Huai-chao1，ZHANG Xue-quan2，LI Hai-feng1
(1.Information Technology Research Base of Civil Aviation Administration of China，Civil Aviation University of China，Tianjin 300300，China; 2.National Space Science Center，Chinese Academy of Sciences，Beijing 100190，China)

During the process of soft-landing for a planetary rover，the parameters of the video navigation system will be changed.There exists the problem about the increased difficulty for the re-calibration of the two cameras.Based on the common stereo rectification algorithm，a weak calibrated stereo rectification algorithm for the visual navigation system of the planetary rover is proposed in this paper.In this algorithm，the rectification matrix is calculated by corresponding points and parameters calibrated on the Earth;the rectification matrix is constrained to ensure that the projection is a homograph transformation whose projection point is the optical center;the computational complexity is reduced by reducing the number of the parameters.The rectification performance comparison experiments between our algorithm and the Euclidean Rectification algorithm have demonstrated the effectiveness of our proposed algorithm.The correction error and the correction distortion are both smaller，which meets the requirements about the vision system of the planetary rover.

Planetary rover;Vision navigation;Stereo rectification;Fundamental matrix;Epiploar geometry

TP752

A

1000-1328(2017)02-0159-07

10.3873/j.issn.1000-1328.2017.02.007

王怀超(1984－)，男，博士，讲师，主要从事图像处理与视觉导航研究。

2016-05-10;

2016-12-04