一种面向复杂探测环境的新型分体式制导策略
李兴龙,姚 郁,杨宝庆
(哈尔滨工业大学控制与仿真中心,哈尔滨150080)
一种面向复杂探测环境的新型分体式制导策略
李兴龙,姚 郁,杨宝庆
(哈尔滨工业大学控制与仿真中心,哈尔滨150080)
针对单一寻的飞行器在具有探测干扰屏障的制导场景中难以精确探测目标的问题,提出一种新型分体式制导策略。该策略采用两个飞行器分别完成对目标的观测与拦截,二者通过合理的信息交互与轨迹配合,从而令拦截器能够间接获取高精度制导信息。首先对分体式制导策略进行数学描述,建立分体相对运动模型和探测模型;然后将拦截器与目标间相对运动状态估计的Cramer-Rao下界作为探测性能指标并进行理论分析,从而指出观测轨迹是提高目标探测性能的关键因素;进而综合考虑目标探测性能与观察器的燃料消耗,将观测轨迹设计问题描述成一个动态多目标优化问题,并给出一种分解优化算法以提高求解效率;最后,仿真飞行算例验证了分体式制导策略的有效性。
分体式飞行器;复杂探测环境;轨迹优化;Cramer-Rao下界;多目标优化
0 引 言
随着当今科技的飞速发展,寻的飞行器所面临的空天战场环境日益复杂,这对飞行器的目标识别、跟踪与检测提出了更高的要求[1]。例如,某些低速或低机动目标会在预警后释放红外烟幕[2]或定向干扰机[3]以干扰寻的飞行器的探测系统,使其探测性能下降甚至致盲,以此达到躲避拦截的目的。针对这一问题,现有的解决方案主要有两种:一是从研发工艺上改良寻的飞行器的探测装置,使之具备更好的目标辨识和抗干扰能力[4-5];二是利用多个飞行器对目标实施同时拦截,以求提高终端命中概率[6-8]。然而上述方案都需要投入较高的资金用于飞行器研发,并且在制导过程中存在一定的风险性,具有作战费效比高的缺点。
值得注意的是,为了解决某些制导场景下的目标探测问题,近年来有学者提出了一种基于功能分离思想的新型制导策略[9-12],该策略采用多个飞行器分别完成对目标的观测与拦截,飞行器之间通过信息交互与轨迹配合,从而令拦截器具备间接获取精确制导信息的能力。例如,文献[9-10]针对空间自主交会场景下的远距离目标相对导航问题,引入了一个辅助观测航天器,从而令交会航天器能够依据双视线测量原理精确获取目标相对距离信息;文献[11]在此基础上将场景扩展至高轨非合作目标制导,并着重对制导信息的滤波算法进行了研究;文献[12]则以空间碎片回收为背景,提出了一种由单一观察器引导多个小型吸附航天器完成碎片回收任务的制导策略,不仅有效降低了制导成本,还可实现对碎片清理效果的近距离观测。考虑到上述制导策略中功能分离的思想与分体式航天器[13]的概念相类似,因此我们将其称为分体式制导策略。从本质上讲,分体式制导策略可以看作是多飞行器协同制导策略的一种特殊形式,但相比于传统以共同拦截为目的的协同制导策略,分体式制导策略能够在保证拦截器制导信息提取精度的前提下,有效降低自身对目标的探测需求,因而具有作战费效比低的优点。
目前国内外对于分体式制导策略的研究成果较少,尚未有学者将其用于解决由红外烟幕或定向干扰机等探测干扰屏障所引起的目标探测问题。但通过分析可知,此类场景下的目标探测问题产生的根源在于寻的飞行器对目标的探测方向与拦截方向在末段制导过程基本重合,此时干扰屏障正好位于寻的飞行器与目标之间,因而会对探测造成不利影响。而如果能够采取合适的分体式制导策略使得飞行器的探测与拦截方向构成一定角度,则有可能规避探测干扰屏障的作用,从而提高拦截器对目标的间接探测精度。因此,本文提出一种新型分体式制导策略用于解决此类场景下的目标探测问题,首先对分体式制导策略进行数学描述,建立带有探测干扰屏障的分体相对运动模型和探测模型;然后选取拦截器与目标间相对运动状态估计的Cramer-Rao下界作为目标探测性能指标,通过分析指出影响分体式制导策略可行性的关键因素;进而对分体式制导策略进行优化设计;最后通过仿真验证分体式制导策略的有效性。
1 分体式制导策略的数学描述
1.1 基本假设
本文所提出的分体式制导策略包含两个己方飞行器,其中用于拦截目标的飞行器称为拦截器,而负责观测目标运动信息的飞行器称为观察器。不失一般性,制导场景中还包含一个目标以及一个探测干扰屏障,如图1所示。图中,观察器与拦截器从同一位置(分离点)出发,分别沿不同的轨迹完成对目标的观测与拦截,拦截器在此期间需要接收并处理观察器的测量数据,方能提取出与目标的相对运动信息用于制导控制。为了便于研究,在此给出如下假设:
1)所有飞行器均为质点并且运行在同一平面内;
2)目标保持静止或匀速运动状态;
3)干扰屏障近似为一圆形区域,其中心位于分离点与目标的连线上,且与目标保持相对静止;
4)所有量测信息的噪声均为高斯白噪声,且当观察器或拦截器与目标的连线与干扰屏障所形成的圆形区域相交时,将会出现目标遮蔽现象,相应量测噪声的方差将显著增大。
基于以上假设,在此对带有探测干扰屏障的分体相对运动模型以及探测模型进行数学描述,以便为后续研究打下基础。
1.2 分体相对运动模型
由于制导场景涉及三个飞行器间的相对运动,分体相对运动模型应当至少由两个不同的二体相对运动模型组合而成。在此将拦截器与目标间的相对运动模型以及观察器与目标间的相对运动模型组合成为分体相对运动模型。
在拦截器视线坐标系下,目标的相对运动方程可以描述如下:
式中:rct和qct分别为目标相对于拦截器的距离和惯性视线角,如图2所示;和分别为拦截器沿视线和垂直视线方向所产生的机动加速度。
同理,可以给出目标在观察器视线坐标系下的相对运动方程,如下式所示
式中:rot和qot分别为观察器与目标间的相对距离和惯性视线角;和分别为观察器沿视线和垂直视线方向所产生的机动加速度。
式中:rco为观察器与拦截器间的相对距离;qco为观察器与拦截器的连线与惯性坐标系Xi轴的夹角,由Xi轴逆时针转向连线方向为正;α与β为三体构型角,如下式所示
从式(3)可以看出,本文所选取的分体相对运动状态可以完整地描述出各飞行器间的相对运动关系。进而根据式(1)和(2),对模型进行一阶泰勒展开,可以得到分体式制导的离散状态方程,如下式所示
式中:Ts为采样周期。
令xk表示k时刻的分体相对运动状态,则式(5)可以简写为以下形式
1.3 分体探测模型
在具有探测干扰屏障的复杂战场环境下,拦截器必须充分利用观察器对目标的测量数据,方能精确提取出目标相对于自身的运动信息。这里,考虑到拦截器与观察器为合作关系,二者的相对位置信息rco和qco可以由两个飞行器的惯性导航装置测量得到,因而根据图2所示的三角关系,观察器只需再对目标的相对距离rot和惯性视线角qot进行测量,即可解算出目标相对于拦截器的相对距离和视线角信息,解算方程如下
式中:
根据这一原理,本文令分体式制导策略中观察器携带距离和角度测量装置分别对rot和qot进行测量,此外,出于精确性和安全性的考虑,拦截器自身还需携带探测装置对目标的视线角qct进行测量。由此给出分体式制导的量测方程如下
式中:ω1~ω5为量测噪声。
值得注意的是,在具有探测干扰屏障的制导场景中,当观察器或拦截器与目标的连线与干扰屏障所构成的圆形区域相交时,量测信息rot,qot或qct的精度将会显著降低。这里,令干扰屏障的中心与目标的距离为d,且大于半径η。易证,当目标遮蔽现象且大于半径η。易证,当目标遮蔽现象出现时,与目标的相对运动状态满足以下不等式
式中:rt和qt分别为制导过程中目标相对于拦截器或观察器的相对距离和惯性视线角;为分离点处目标相对于拦截器的惯性视线角。
式(9)表明在具有探测干扰屏障的制导场景中,量测噪声不仅取决于飞行器探测装置的固有性能,还与当前时刻飞行器所处的位置密切相关。因此,量测方程(8)可以改写为以下形式
式中:zk为k时刻的量测输出;ωk为统计特性与当前时刻状态xk有关的量测噪声。
需要指出的是,在实际的制导过程中由于存在量测噪声和通信延迟,拦截器不能直接依据解算方程(7)生成制导指令,而是需要对接收到的观察器的量测数据进行坐标变换、延迟补偿以及融合滤波等多个操作,方能提取出精确的目标相对运动信息用于制导控制,制导信息的提取框图如图3所示。
2 分体式制导策略的探测特性分析
为了从理论上说明本文所提出的分体式制导策略的有效性,需要首先选取合适的物理量来表征拦截器对目标的间接探测性能,并以此揭示出影响分体式制导策略可行性的关键因素,以便开展针对性设计。结合上一节所建立的分体相对运动模型和探测模型,图3所示的拦截器制导信息提取过程本质上是要依据已有量测数据对拦截器与目标间的相对运动状态进行非线性估计。根据参数估计的相关理论,在此引入如下引理
引理1[14].(Cramer-Rao不等式)假设观测样本Z中隐含有真实参数θ,p(Z|θ)是其条件分布密度函数,并且和都存在。则依据Z对θ进行无偏估计所能达到的均方误差下界等于其Fisher信息的逆,即
不等式(11)等号成立的充要条件是存在一个关于θ的函数W(θ),使得下式成立
对于多参数情形,不妨记θ=[θ1,θ2,…,θn]T,此时Fisher信息变为Fisher信息矩阵F(θ),其元素Fij(θ)定义为
相应的Cramer-Rao不等式变为矩阵不等式
式中:C(θi)表征参数θi估计的Cramer-Rao下界,即估计均方误差所能达到的下界。
由定理1可知,参数估计的Cramer-Rao下界与具体的滤波算法无关,其表征从实际观测样本中提取出真实参数的潜力。该值越小,说明参数的能观测性越好,对量测误差的敏感度越低。考虑到Cramer-Rao下界具有明确的物理意义,且计算过程较为简便,本文将拦截器与目标间相对运动状态估计的Cramer-Rao下界作为分体式制导策略的目标探测性能指标。
值得注意的是,拦截器与目标间的相对运动状态是分体相对运动状态的一部分,因此其估计的Cramer-Rao下界可以根据分体相对运动方程和量测方程计算得到。这里,对于任意K>0时刻,令xK表示真实的分体相对运动状态,观测样本ZK可以描述如下
式中:zK-N+1~zK为K时刻之前一段时间内的N个量测输出,1≤N≤K;为系统根据先验信息获得的当前时刻状态预估值,服从如下正太分布
式中:SK≥0为K时刻的系统状态预估的协方差矩阵,表达式如下
式中:Srct~Sdqot为状态分量预估的方差值。
由于量测噪声也服从高斯分布,系统状态xK的条件分布密度函数可以表示如下
式中:n和m分别为系统状态和量测输出的维数,易知n=8,m=5;Ri≥0为i时刻量测噪声的协方差矩阵,表达式如下
式中:Rrco~Rqct表示i时刻每个量测信息的噪声方差值,根据之前的叙述可知,其不但取决于飞行器探测装置的固有性能,还与当前的分体相对运动状态相关。考虑到rco和qco是由己方飞行器的惯导装置测量得到的,这里可以假定拦截器与观察器之间相对信息的探测精度满足如下关系式
将式(20)代入式(12),可得Fisher信息矩阵的表达式,如下式所示
令
将式(24)和(25)代入式(23),可得
对式(26)求逆即可得到分体相对运动状态估计的Cramer-Rao下界,即拦截器对目标的间接探测性能指标。从中不难看出,由于分体相对运动状态xK会在制导过程中不断变化,这使得拦截器对目标的间接探测性能也会呈现出复杂时变特性。为了定量分析影响目标探测性能的主要因素,在此考虑拦截器仅利用当前时刻的量测信息对系统状态进行估计,即N=1,此时Φi,K恒为单位阵,相应的Fisher信息矩阵可以简化为
考虑到探测装置对分体相对运动状态的直接量测误差通常远低于状态预估值的误差,即Rrot<<Srot,Rqot<<Sqot,Rqct<<Sqct,因而可对式(27)进行进一步简化并求逆,从而得到拦截器与目标间惯性视线角qct估计的Cramer-Rao下界解析表达式,如下式所示
对上式进行整理,可以得出以下不等式
式中:当且仅当rct=0时等号成立。式(29)表明分体式制导策略中拦截器由于融合了观察器的探测信息,使得其对目标惯性视线角的探测精度将始终优于仅依赖自身探测装置对目标的探测精度;其次,从式(28)可以看出随着方差Rrot和Rqot的减小,qct的探测性能将显著提升,这说明观察器若能够主动规避探测干扰屏障以实现对目标的精确测量,将有助于拦截器获取更加精准的目标视线角信息。再次,qct的探测性能也与方差Rrco有关,通过提高观察器与拦截器惯性导航装置的测量精度也会对拦截器制导信息的精确提取起到促进作用。最后,qct的探测精度还可通过飞行器三体构型参数β、rot以及rct进行调节,因而在设计观察器和拦截器的飞行轨迹时,应当考虑令飞行器间维持良好的三体构型关系,以便提高探测精度。
同理,可以得到拦截器与目标间相对距离rct估计的Cramer-Rao下界解析表达式,如下式所示
对式(30)进行整理,可得
从式(31)可以看出,观察器相距目标越近,拦截器对目标的距离信息估计越准确,并且通过优化构型角β,可以进一步提高拦截器与目标间相对距离的探测精度。
综合以上分析结果,拦截器在探测干扰屏障作用下的目标探测性能不但取决于探测装置的测量精度,还与观测与制导轨迹密切相关。其中,拦截器制导轨迹设计的目的是消除其与目标间的制导偏差,考虑到自身过载和燃料的限制,其在末段制导过程中很难大幅改变拦截角度以规避探测干扰屏障。因此拦截器制导指令{}只需依据现有成熟导引律进行设计即可,而拦截器制导信息的精确提取将主要依赖于观察器制导指令{}的优化设计,也就是说,观测轨迹是影响分体式制导策略可行性的关键因素,有必要对其进行优化设计。
3 分体式制导策略的优化设计
通过上一节对分体式制导策略的探测特性分析可知,分体式制导策略设计的核心在于如何优化观察器的制导指令{},使之能够为拦截器实现高精度目标探测提供有利条件。相比于传统侦察任务下的观测轨迹设计[15-16],分体式制导策略中的观测轨迹设计不仅要保证观察器与目标间的相对运动关系满足基本探测要求,还要令观察器能够尽早脱离探测干扰屏障的影响,并与拦截器和目标维持良好的三体构型关系,这对于轨迹优化指标以及优化方法都提出了新的要求。因此,本节着重对此问题进行研究工作。
3.1 优化问题描述
在优化观测轨迹时,本文结合实际制导任务需求,提出以下两个优化指标:
指标1:目标间接探测性能
本文所提出的分体式制导策略的目的即是要解决拦截器在具有探测干扰屏障作用下的目标探测问题,因此应将拦截器对目标的间接探测性能作为观测轨迹设计的一个优化指标。这里,考虑到拦截器与目标间的惯性视线角qct通常是制导所需的关键信息,因此可将其估计的Cramer-Rao下界作为瞬时目标间接探测性能。值得注意的是,由于拦截器对目标的间接探测性能具有时变性,若仅以某一时刻的瞬时探测性能作为优化指标,将不能真实反映出拦截器在制导过程中的整体探测精度。为此,本文将qct在一段时间内的估计标准差下界的平均值作为观测轨迹优化的性能指标,即
式中:K1和K2为分体式制导过程的两个重要时间节点,在此期间拦截器需要获取高精度的制导信息用于修正制导偏差。需要指出的是,由于观察器的变轨机动通常也会对目标的观测造成不利影响,本文要求观察器在此期间无轨控飞行。
指标2:观察器的燃料消耗
在提升拦截器对目标的间接探测性能的同时,观察器到达指定观测位置所需的燃料消耗也是观测轨迹设计应当考虑的重要因素,其直接关系到分体式制导策略的成本与工程可实现性。因此,本文将观察器控制指令的能量积分作为另外一个优化指标用于观测轨迹设计,即
在优化指标确立的基础上,对于观测轨迹的设计还应当保证观察器与目标之间的相对运动状态能够满足观察器探测装置的目标探测要求,在此提出以下两个约束条件:
约束1:视线角速度约束
在分体式制导过程中,观察器并不以拦截目标为目的,这使得目标相对于观察器的视线变化率可能发生较大变化。考虑到观察器需要始终对目标进行跟踪观测,若视线变化率超过观察器姿态所能跟踪的最大角速率,观察器将会丢失目标,从而导致探测失效。因此,在设计观测轨迹时应当保证观察器与目标间的视线角速率始终在允许的范围内,即
式中:ωom为观察器所能跟踪的最大视线角速率。
约束2:相对距离约束
考虑到观察器的探测装置一般存在探测量程与盲区,因此在设计观测轨迹时应当令观察器与目标之间的相对距离保持在可探测范围之内,即
式中:rmin和rmax为观察器探测的最近与最远距离。
综上所述,本文将观测轨迹设计问题描述成为一个带有约束的动态多目标优化问题,如下式所示
式中:系统的初始状态x0以及拦截器控制输入序列{}已事先给定。
3.2 主要结果
对于多目标优化问题而言,由于指标之间具有不可公度性和矛盾性,导致一般不存在全局最优解,取而代之的是一个由非劣解所构成的集合,称为Pareto最优解集[17]。设计者需要从此集合中选取偏好解作为优化问题的最终解,因而实际计算得到的Pareto最优解集的规模与分布将直接影响到设计者对于最终解的满意程度。目前,国内外对于静态多目标优化问题已经提出了多种数值优化算法[18-20],可以通过一次数值仿真获得大量Pareto最优解,而对于动态多目标优化问题的求解一直是一个具有挑战性的工作[21]。目前工程上常见的解决思路是采用指标加权的方式,将其转化成为一个动态单目标优化问题,通过数值计算获得一个Pareto最优解。这种方式对于加权系数的选取要求较高,并且需要大量的数值仿真才能获得具有一定规模和分布的Pareto最优解集,具有计算效率低的缺点。针对这一问题,本文结合自身优化问题的特点,提出一种分解优化算法,通过引入适当的中间变量,将原优化问题进行合理的分解,从而利用现有优化工具即可通过一次数值计算获得大量Pareto最优解。
根据前文的叙述,本文要求观察器在K1至K2期间无轨控飞行,所以系统在此期间的任意状态都可以由K1时刻的状态x1外推得到。因此,优化指标J1可以看作是x1的函数,进而将x1作为中间变量引入到原始优化问题中,可以进行等效拆分。
证.先证充分性,采用反证法。假设优化问题SP1和SP2的解不是优化问题P的Pareto最优解,则必然存在一组P的Pareto最优解{u'k},使得
式中:x'1是根据x0和{u'k}推导得到的K1时刻系统状态,易证(x'1)≤J2({u'k})。将其代入式(39)可得
由上式可知,在优化问题SP2中x'1的所有性能都优于且满足约束条件,因此不是SP2的Pareto最优解,与前提条件矛盾,充分性得证;
再证必要性,采用反证法。假设优化问题P的Pareto最优解不是SP1和SP2的最优解,则必然存在一组SP1和SP2的最优解x'1和{u'k},使得
在优化问题P中,由式(41)可知{u'k}所对应的性能指标都优于 {}且满足约束条件,因而{}不是Pareto最优解,与前提矛盾,必要性得证。
从式(37)和(38)可以看出,优化问题SP1属于一类边界给定情况下的动态单目标优化问题,可以采用序列二次规划的方法[22]得到任意x1所对应的性能指标。在此基础之上,优化问题SP2属于一类带有多约束的静态多目标优化问题,通过遗传算法即可对x1进行寻优,从而获得大量Pareto最优解。设计者从中选取偏好解作为最终解,所对应的SP1的最优解{}即为最优的观测轨迹控制序列。
4 仿真校验
本节以拦截某型低机动目标飞行器为例,考虑其会在感知威胁后释放出红外烟幕以干扰寻的飞行器的光学探测装置,在此对本文所提出的分体式制导策略进行仿真验证。制导场景的基本参数由表1给出。
借鉴文献[23]关于光学探测系统以及惯性导航系统的相关参数,这里令观察器或拦截器对目标的正常测角精度为Rqot=Rqct=10-6rad2;观察器对目标的测距精度为Rrot=10 m2。由于观察器与拦截器为合作关系,并且在末段从同一位置分离出发,因而二者之间相对信息的测量精度将明显优于对目标的测量精度,不妨取Rrco=1 m2。当制导过程中观察器或拦截器与目标的相对运动状态满足式(9),即出现目标遮蔽现象时,令与之对应的量测噪声的方差Rqot,Rrot或Rqct放大100倍。此外,观察器探测装置的有效探测距离为50~10000 m,观察器所能跟踪的最大目标视线角速度为0.17 rad/s。
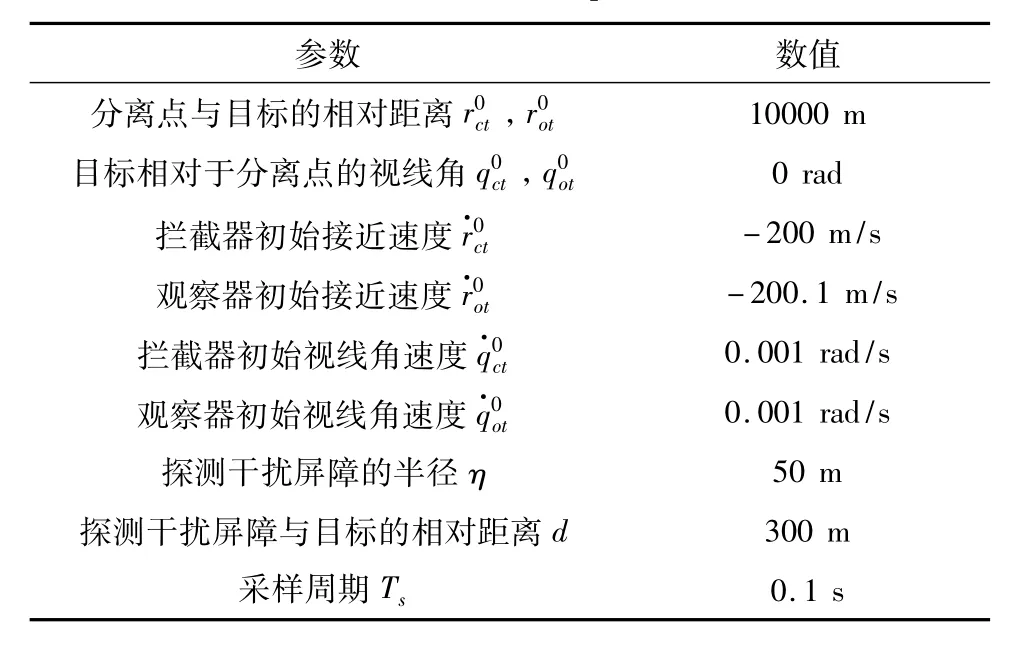
表1 仿真参数Table 1 Simulation parameters
在计算式所示的Fisher信息矩阵时,通过观察可以发现状态估计误差的方差阵Sk与分体相对运动状态xK并无耦合作用,因此Sk只会影响探测性能指标的绝对数值,而其并不会对观测轨迹优化结果产生实质性影响。这里令
在设计观测与制导指令时,本文令拦截器采取比例导引的方式向目标接近,导引系数为4;而观察器以制导过程最后15 s的制导信息探测性能作为优化指标,寻求最佳观测轨迹。采用NASA-II遗传优化算法求解式(38)所示的多目标优化问题,算法的具体参数由表2给出
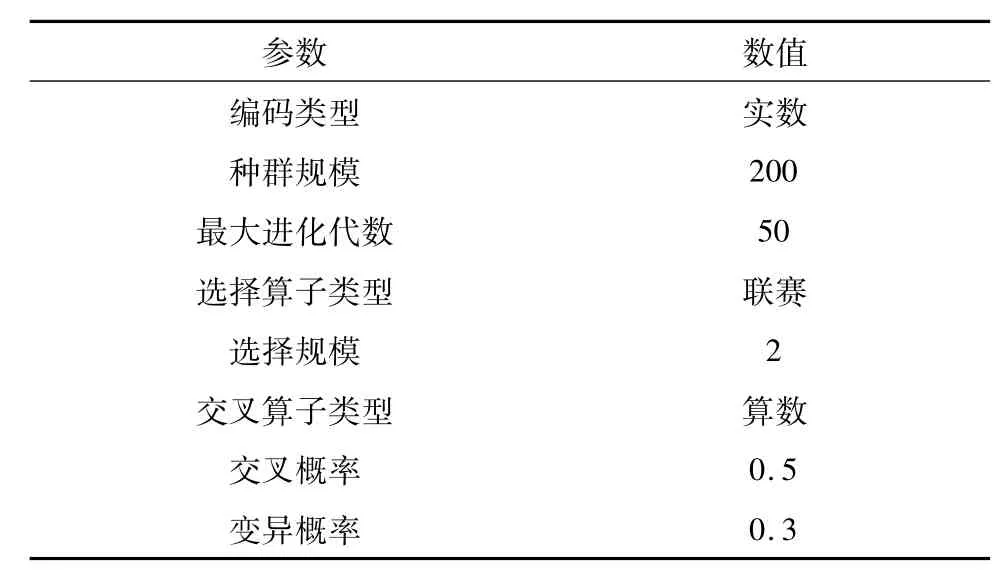
表2 NASA-II遗传优化算法的相关参数Table 2 Parameters of NASA-II
考虑到遗传算法具有随机性,本文在求解时共进行10次重复数值仿真,并去除重复解以及错解,从而得到一组由138个Pareto最优解所构成的集合,Pareto解前沿由图4给出。从图中可以看出,优化指标J2随着J1的增大而减小,说明了本文所研究的观测轨迹优化问题不存在全局最优解。
综合考虑目标探测性能与观察器的燃量消耗,这里选取指标J1=10-4rad,J2=254 m2/s3所对应的Pareto最优解作为轨迹优化问题的最优解,对应的K1时刻系统状态为
图5为根据上述优化结果得到的分体式制导轨迹,从中可以看出随着制导过程的进行,拦截器的制导方向与观察器的观测方向将逐渐发生改变,并且观察器在第26.8 s后开始摆脱探测干扰屏障的影响,而拦截器在制导全程都处在遮蔽区域内。制导过程中观察器与目标之间的相对距离和视线角速度变化曲线由图6给出。不难看出,二者之间的相对运动状态在到达K2时刻之前均能满足观察器探测距离以及视线角速度的约束。
在此基础上,为了说明优化设计的分体式制导策略能够有效提高拦截器对目标的间接探测性能,在此给出一组对比仿真实验。分别选取传统单体制导策略(即不考虑观察器与拦截器之间的信息交互)以及未进行观测轨迹优化的分体式制导策略作为对比量,其中,未优化的观测轨迹在K1时刻的观测状态为
三种不同制导策略下的制导信息qct的估计标准差下界由图7给出。从中可以看出,两种不同观测轨迹下的分体式制导策略所对应的探测性能都优于单体制导策略,这与根据式(29)所得到的理论分析结果相吻合。但由于在制导过程前期观察器也处于目标遮蔽区域内,导致其自身对目标探测精度较低,因而拦截器对目标的间接探测性能的提升幅度不大。但是在优化的分体式制导策略中,目标探测性能在第26.8 s明显提升,这是由于观察器此时刚好飞出遮蔽区域,此时量测方差Rrot和Rqot大幅降低,从而令qct估计的Cramer-Rao下界也随之减小。
为了进一步说明优化的分体式制导策略可以提高实际制导信息的提取精度,这里采用扩展卡尔曼滤波器对K1至K2时间段内的拦截器制导信息进行非线性估计。在相同初始仿真条件下,拦截器视线角估计误差的曲线如图8所示,可以看出,优化的分体式制导策略下的信息估计误差收敛速度及数值都明显低于单体制导策略以及未进行观测轨迹优化的分体式制导策略。
考虑到滤波过程带有随机性,这里对三种不同制导策略分别进行50次蒙特卡罗仿真,拦截器视线角在K1~K2期间的估计误差平均值由图9给出。从图中可以看出,在同等仿真条件下优化的分体式制导策略所对应的qct估计精度相比于单体制导策略大致提升了一个数量级,这一方面说明本文基于Cramer-Rao下界所提出的优化指标可以很好的反映出拦截器实际目标间接探测性能,另一方面也验证了通过优化分体式制导的观测轨迹可以对拦截器制导信息的精确提取起到促进作用。
5 结 论
本文的主要创新工作在于提出并初步论证了一种新型分体式制导策略,用于解决探测干扰屏障作用下的目标探测问题。文中重点围绕分体式制导策略的数学描述、探测特性分析以及轨迹优化设计开展了理论研究。首先根据分体相对运动模型和探测模型,推导出了拦截器对目标运动状态估计的Cramer-Rao下界,并以此分析出了目标间接探测性能具有时变性并且与观测轨迹密切相关;然后综合考虑目标探测性能与观察器的燃料消耗,将观测轨迹设计问题描述成一个动态多目标优化问题,并给出了一种分解优化算法,有效提高了求解效率。仿真对比结果表明,优化后的分体式制导策略可以显著提高拦截器在复杂探测环境下的目标探测精度,从而验证了分体式制导策略的有效性。
[1] 姚郁,郑天宇,贺风华,等.飞行器末制导中的几个热点问题与挑战[J].航空学报,2015,36(8):2696-2716.[Yao Yu,Zheng Tian-yu,He Feng-hua,et al.Several hot issues and challenges in terminal guidance of flight vehicles[J].Acta Aeronautica et Astronautica Sinica,2015,36(8):2696-2716.]
[2] Wang L,Jiang N,Lv M.Research into the usage of integrated jamming of IR weakening and smoke-screen resisting the IR imaging guided missiles[C].Proceedings of SPIE-Optical and Optoelectronic Sensing and Imaging Technology,Beijing,China,May 5-7,2015.
[3] 范晋祥,李亮,李文军.定向红外对抗系统与技术的发展[J].红外与激光工程,2015,44(3):789-794.[Fan Jinxiang,Li Liang,Li Wen-jun.Development of direct infrared countermeasure system and technology[J].Infrared and Laser Engineering,2015,44(3):789-794.]
[4] Smith C R,Grasso R,Pledger J,et al.Trends in electro-optical electronic warfare[C].Proceedings of SPIE-Technologies for Optical Countermeasures IX,Edinburgh,United Kingdom,September 26-27,2012.
[5] 高颖慧,王平,李君龙,等.复杂战场环境下的防空反导光学成像制导技术[J].现代防御技术.2012,40(1):6-10.[Gao Ying-hui,Wang Ping,Li Jun-long,et al.Optical imaging guidance technology in complicated battlefield environment[J].Modern Defense Technology,2012,40(1):6-10.]
[6] Zhang Y,Wang X,Wu H.A distributed cooperative guidance law for salvo attack of multiple anti-ship missiles[J].Chinese Journal of Aeronautics,2015,28(5):1438-1450.
[7] 谢愈,刘鲁华,汤国建,等.多拦截器总体拦截方案设计与分析[J].北京航空航天大学学报,2012,38(3):303-308.[Xie Yu,Liu Lu-hua,Tang Guo-jian,et al.Design and analysis of interception project for multiple kill vehicle interceptor[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(3):303-308.]
[8] Shaferman V,Shima T.Cooperative optimal guidance laws for imposing a relative intercept angle[J].Journal of Guidance,Control,and Dynamics,2015,38(8):1395-1408.
[9] Chen T,Xu S.Double line-of-sight measuring relative navigation for spacecraft autonomous rendezvous[J].Acta Astronautica,2010,67(1-2):122-134.
[10] Chen T,Xu S.Approach guidance with double-line-of-sight measuring[J].Journal of Guidance,Control,and Dynamics,2011,34(3):678-687.
[11] 高学海,梁斌,潘乐,等.高轨非合作目标多视线分布式相对导航方法[J].宇航学报,2015,36(3):292-299.[Gao Xue-hai,LiangBin,Pan Le,etal.Distributed relative navigation of GEO non-cooperative target based on multiple lineof-sight measurements[J].Journal of Astronautics,2015,36 (3):292-299.]
[12] Li X,Yao Y,Yang B.Guidance strategy design for space debris removal usingfractionated spacecraft[C].IEEE Chinese Guidance,Navigation,and Control Conference,Nanjing,China,August 12-14,2016.
[13] Brown O,Eremenko P.Fractionated space architectures:A vision for responsive space[C].The 4th Responsive Space Conference,Los Angeles,CA,USA,April 24-27,2006.
[14] 张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[15] Yao Y,Xie R,He F.Flyaround orbit design for autonomous rendezvous based on relative orbit elements[J].Journal of Guidance,Control,and Dynamics,2010,33(5):1687-1692.
[16] 张庆展,曾占魁,靳永强,等.空间快速绕飞与视线指向的建模与控制[J].宇航学报.2014,35(3):324-330.[Zhang Qing-zhan,Zeng Zhan-kui,Jin Yong-qiang,et al.Modeling and control on fast fly-around and line of sight pointing[J].Journal of Astronautics,2014,35(3):324-330.]
[17] 徐玖平,李军.多目标决策的理论与方法[M].北京:清华大学出版社,2005.
[18] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm: NSGA II[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[19] Fonseca C M,Fleming P J.Genetic algorithms for multiobjective optimization:formulation,discussion and generalization[C].InternationalConferenceon GeneticAlgorithms,Michigan,USA,July 19-23,1999.
[20] Zhang Q,LiH. MOEA/D: a multiobjectiveevolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Computation,2007,11(6):712-731.
[21] Muruganantham A,ZhaoY,GeeS B,etal.Dynamic multiobjective optimization using evolutionary algorithm with Kalman filter[C].17th Asia Pacific Symposium on Intelligent and Evolutionary Systems,Seoul,South Korea,November 7-9,2013.
[22] 何坚勇.最优化方法[M].北京:清华大学出版社,2007.
[23] 张淑琴,王忠贵,冉隆燧.空间交会对接测量技术及工程应用[M].北京:中国宇航出版社,2005.
通信地址:哈尔滨市南岗区一匡街2号3008信箱(150080)
电话:(086)13845062668
E-mail:xingl.lee@gmail.com
(编辑:张宇平)
A Novel Fractionated Guidance Strategy for Complicated Detection Environment
LI Xing-long,YAO Yu,YANG Bao-qing
(Control and Simulation Center,Harbin Institude of Technology,Harbin 150080,China)
To deal with the target detection problem in the complex interception engagement where some jamming barriers exist,a novel fractionated guidance strategy is presented.In this strategy,two flight vehicles are adopted to implement target observation and interception respectively,and high precision guidance information can be obtained indirectly via proper information fusion and trajectories design.The fractionated guidance engagement is described firstly in terms of mathematical models of relative motion and detection.Then the detection characters of fractionated guidance are analyzed in terms of the estimated Cramer-Rao low bound of the relative states between the interceptor and target.The analysis results show that the observation trajectory is of critical importance to the improvement of target detection.Furthermore,the observation trajectory design problem is formulized as a multi-object dynamic optimization problem with the tradeoff between the target detection accuracy and the observer’s fuel consumptions.To improve the numerical calculation efficiency of the problem,an optimization algorithm based on decomposition is introduced.Finally,the validness of the proposed fractionated guidance strategy is demonstrated by simulation results.
Fractionated flight vehicles;Complicated detection environment;Trajectory optimization;Cramer-Rao low bound;Multi-object dynamic optimization
TP273
A
1000-1328(2017)02-0131-12
10.3873/j.issn.1000-1328.2017.02.004
李兴龙(1986-),男,博士生,主要从事多飞行器协同探测制导技术的研究。
2016-07-22;
2016-11-30
国家自然科学基金(61473099,61333001)

