乒乓球战术行为策略选择博弈矩阵的构建

岳海鹏

乒乓球战术行为策略选择博弈矩阵的构建

岳海鹏

竞技运动不仅要有强劲的素质和稳定的心理，还必须掌握大量的战术信息。战术行为策略是指为达到某个战术目的而采用的具有战术意义的动作系列或动作组合，乒乓球战术行为的博弈矩阵构建是对运动员的策略选择进一步量化分析的必由之路和必要手段。研究发现，乒乓球运动从一板球的角度来看并非零和博弈，而是一种变和博弈，建立了乒乓球博弈双方运动员战术行为选择的策略库集S，并在子博弈的基础上构建了战术行为策略选择的博弈矩阵，构建的矩阵是进一步量化研究并获得良好博弈模型的基础。

乒乓球运动；战术博弈；行为策略选择；博弈矩阵

随着竞技体育竞争的白热化，仅靠优秀的身体素质和高昂的精神状态已很难获胜，获取并分析对手的战术信息，有针对性地制定战术并在赛场上灵活运用，成为获胜的重要保证。

战术行为策略是指为达到某个战术目的而采用的具有战术意义的动作系列或动作组合，而战术行为与竞技要素与制胜因素密切相关。虞丽娟指出乒乓球比赛战术行为的基础观察指标一般分为击球技术、击球位置、击球线路(落点)和比赛行为[1]。张辉引入了马尔可夫链，建立球类比赛状态(技术或战术)的转移概率矩阵，他把乒乓球比赛典型的战术行为状态划分为发球、接发球、相持、进攻、防守、控制(一个回合结束状态的)及得分，认为马尔可夫性就是比赛中的下一个战术行为状态仅和现在的战术行为状态相关，而与其上一个战术行为状态无关[2]。

张辉的描述实际上反映了乒乓球运动中上一次击球和下一次击球的关系，而这样的关系实质上是运动员的战术行为策略选择过程，是博弈矩阵的概率选择，这样的矩阵是双方运动员博弈的核心。乒乓球战术行为的博弈矩阵构建过程是对运动员的策略选择进一步量化分析的必由之路和必要手段。

1 体育界对博弈的研究

体育博弈，是在一定的竞争规则的限定下进行的最具理想意义的竞争。随着体育运动实践的发展，各种冲突、对抗与竞争表现出鲜明的博弈特征，促进了体育博弈理论的形成[3]。虽然“博弈”一词有浓浓的中国古代特色，但是“博弈论”起源于西方，引入中国也在上世纪80年代，主要研究还是在经济学领域。此后，体育界逐渐重视博弈论的研究，分别从各个项目和各个角度研究了体育博弈论[4-8]。这些研究多数是从宏观博弈的角度解决认识论的问题，偶尔有微观的博弈分析，也仅仅局限于“囚徒困境”一类的简单案例，例如，张晓昌用纳什均衡来解释羽毛球发球的混合策略[9]。

运动员在场上运用战术实际上是一个博弈，一方运动员有多种战术使用，而对方运动员也可有多种战术可以使用，双方各种战术的对垒会产生不同的结果，且各方都希望从中获利，这就是一种具体的博弈。

刘文明的研究在此基础上更进了一步，他以实证的态度选取了运动员的落点策略和技术策略建立博弈矩阵，分析运动员的具体得益，从中构建乒乓球战术行为博弈分析模型，求解各阶段博弈模型的“纳什均衡”[3]。他的研究主要在静态博弈中的纳什均衡。从乒乓球的表现形式上看，它是一个动态的博弈过程，运动员的策略选择是依次选择行为，而不是同时选择行为。从博弈的类型分析，它有四种不同类型，相对应有四个均衡，即：纳什均衡、子博弈完美纳什均衡、贝叶斯纳什均衡和完美贝叶斯纳什均衡[10]。如何寻找运动员战术行为策略的贝叶斯纳什均衡，在其动态博弈过程能为运动员的策略提供依据，重点找出两板之间的联系，设定策略矩阵，帮助其建立自身的战术体系是今后努力的方向。

2 乒乓球运动员战术行为策略的划分标准

乒乓球运动员战术行为选择的策略不仅包括上述的速度策略和线路策略，还应该包括运动员针对博弈对手所采用的具体战术单元。运动员所采用的战术包括三个层面的内容，分别是战术风格、战术组合和战术单元。战术风格是一个运动员具体战术组合所呈现出来的稳定的战术体系特征，它所对应的是技术体系中的类型打法，战术风格属于整体的上位概念，量化比较困难；战术组合对应着技术体系的若干结合技术组合，是战术中的中位概念；战术单元是策略化了的单一技术，能够具体到某一技术，量化起来比较容易，如图1。

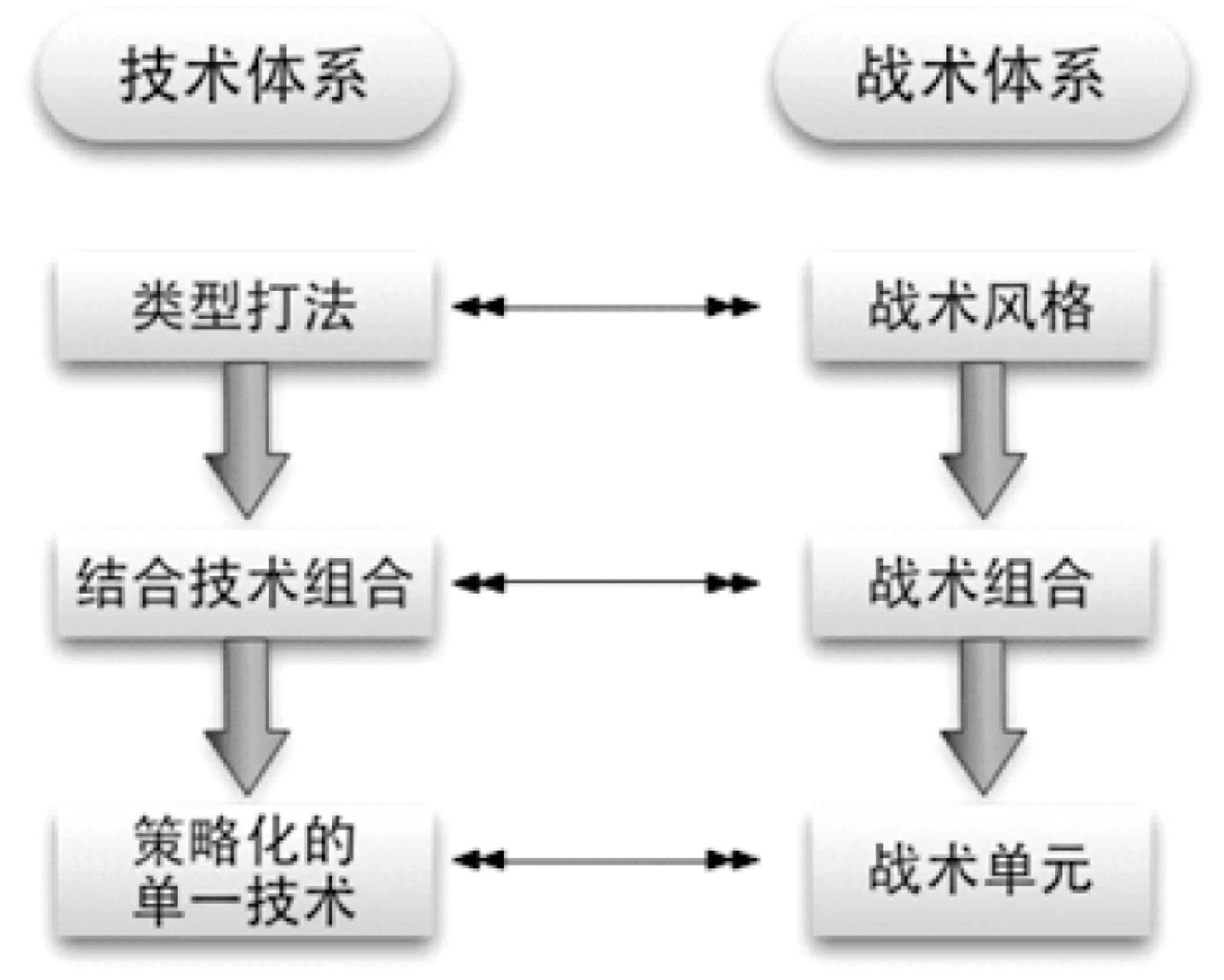
图1 技术体系和战术体系的对应关系

一种战术风格的形成由若干的战术单元所构成，具体地说就是某一项具体的技术，这种策略化的单一技术被唐建军[11]称之为战术的“细胞”，是战术行为选择的最小单位。

乒乓球界历来对战术指标的建立尤为重视，在多年的比赛实践中，相对确定了比较固定诊断指标，诊断指标体系的确定从实践中的实际需要开始，经过实战的筛选，回到实践检验的过程。张晓蓬[12]认为，经过第24、25、26、27届奥运会和期间的4届亚运会及7届世界锦标赛备战的检验，证明是可靠的。从表1、2能够看出，其中的四级和五级基本可以认为是博弈双方运动员选择战术的具体行为表现。

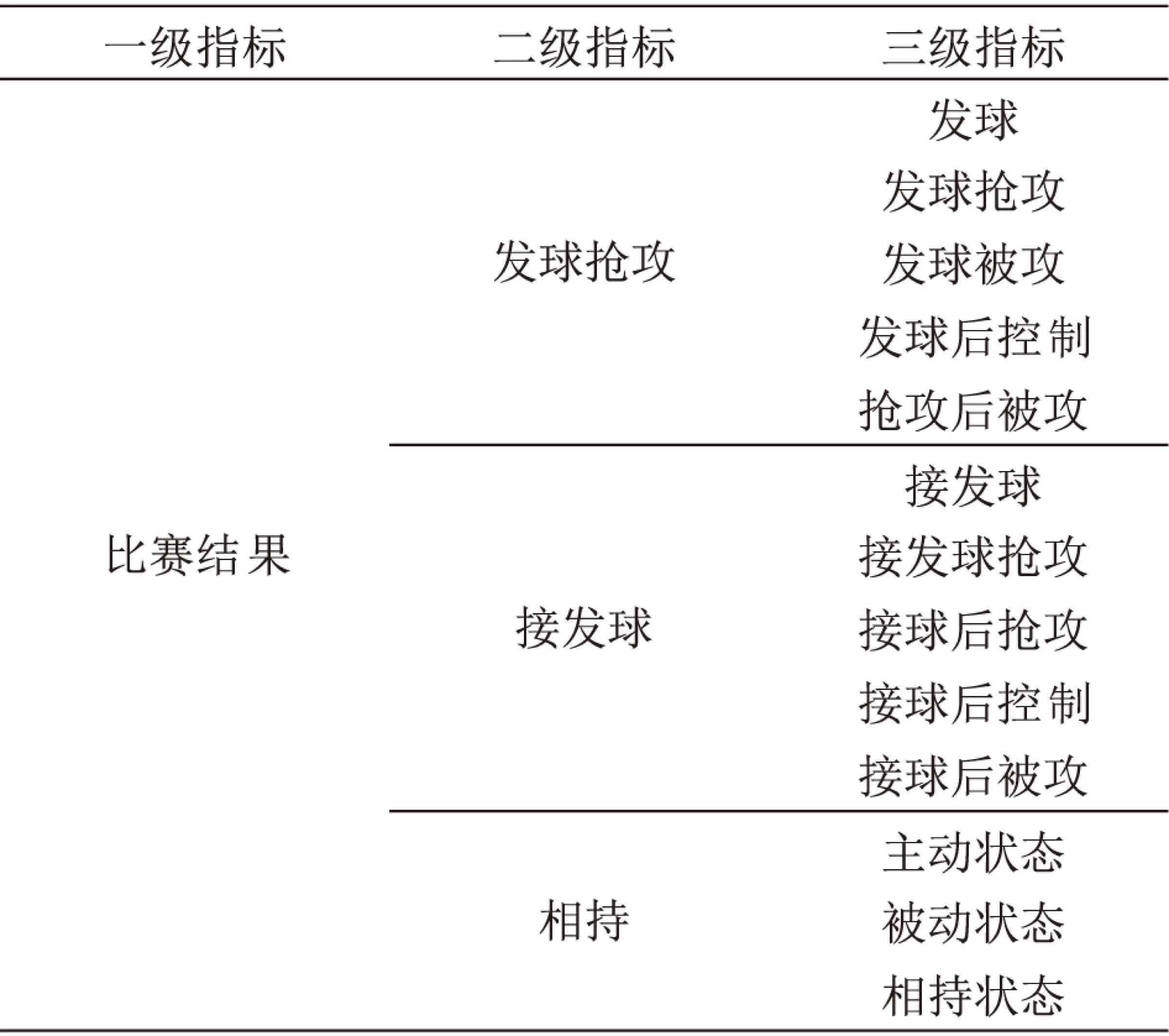
表1 战术诊断指标体系

表2 战术诊断比赛效果的四级和五级指标[12]

因此，将乒乓球运动员战术行为策略的划分标准以战术单元为最小单位，符合构建模型的抽象性和可量化性的基本原则，并结合表2中四级指标中的“手段”，对具体战术单元采用的手段加以区分，并作为博弈双方运动员战术行为选择的策略库集S，如表3。

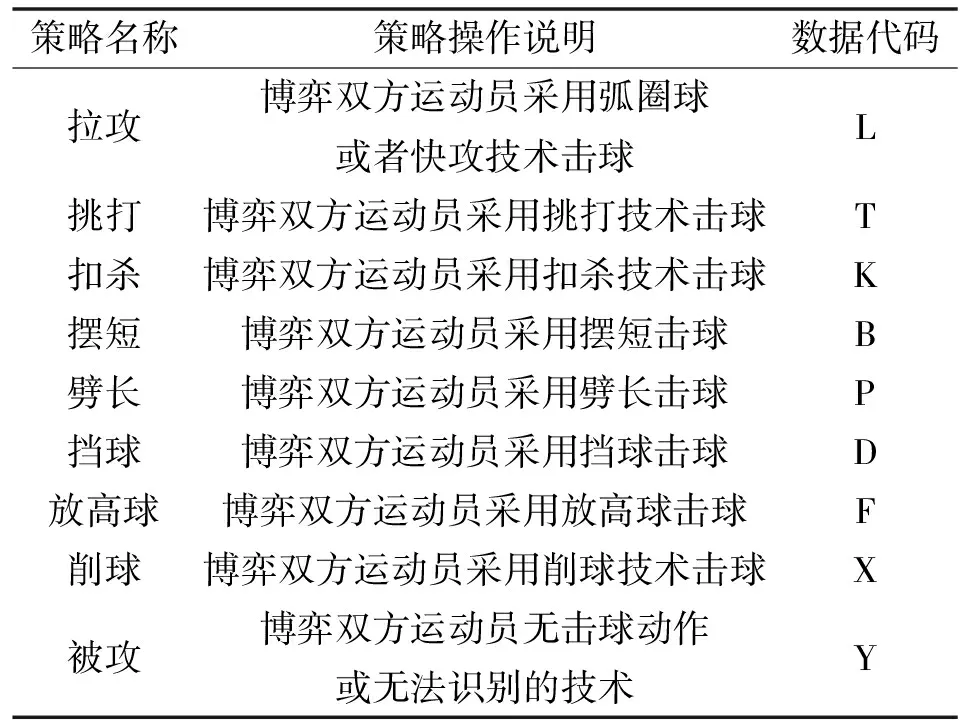
表3 手段策略指标

3 博弈矩阵的构成要素

博弈即一些个人、队组或者其他组织，面对一定的环境条件，在一定的规则下，同时或先后，一次或多次，从各自允许选择的行为或策略中进行选择并加以实施，各自取得相应结果的过程[13]。博弈包含的基本要素有：参与者(Players)、策略(Strategies)或行动(Actions)、次序(Orders)以及获益(Payoffs)。这些信息整合起来被称为博弈规则(Rules of the Game)，构建模型的目的是根据博弈规则来描述战术博弈这种现象，解释在规则的范畴内可能发生什么情况。而乒乓球运动员则根据每个时段得到的信息，做出自己的战术选择，也就是策略(Strategies)，并尽量使自己的利益最大化，争取比赛的主动直到获得这一分。双方运动员选择的策略组合在一起能够形成一种均衡(Equilibrium),有了这种均衡，我们可以从中得出博弈双方运动员策略组合的各种可能，进一步获得了博弈的结果(Outcome)。

3.1 博弈的参与者(Players)

参与者(Players)是指进行策略选择的个体，每个参与者的最终目标是依靠这种策略选择来使自身的获益最大化。在现实的博弈中，存在单人博弈、双人博弈和多人博弈。在乒乓球比赛中，有单打比赛和双打比赛(本文仅研究单打比赛)，但是双打比赛可以将配对的一对选手视为一方，所以在场上直接参与博弈的是属于双人博弈。不过，在比赛过程中，并非仅仅是运动员参与，教练员甚至科研人员都参与其中，而且双方教练员对决策也起着至关重要的作用，在这种情形下就出现了多人博弈。由于体育项目多人博弈多变性以及量化难度大，导致建立多人博弈模型的条件并不成熟，所以本文仅研究双人博弈模型的构建。因此对所有的博弈运动员都称为博弈参与者i。

3.2 各博弈方各自可选择的策略(Strategies)集合

策略集即规定参与者i在进行策略选择时，可供选择的方法或者量值等。在不同的博弈中参与者i可以选择的策略数量是不同的；而在同一个博弈中，不同参与者i的可选策略的内容和数量也经常不尽相同，往往只有有效的几种，乃至一种，也有可能是很多种，甚至无限多。

前文已经就研究所需要的策略集合进行了详细的划分，下面对策略集合做一般性的描述。每一个参与者i的所有可供选择的策略集合之和称为“策略空间”，分别用S1,…,Sn表示Si∈Sij表示参与者i的第j个策略，其中j可为有限值，也可为无限值，本文的策略空间为有限个值的有效策略博弈。

3.3 进行博弈的次序(Orders)

在各式各样的决策活动中，博弈的参与者i进行独立决策时，拿出或者选择策略的次序方式有两种，一种是要求博弈双方同时作出选择，或者虽然博弈双方没有同时选择，但是其双方都不知晓对方的选择策略，我们称为同时选择；另一种是博弈双方作出的选择有先后之分，我们称为依次选择。第一种博弈过程称之为“静态博弈”(StaticGames)，平时我们玩的“石头、剪刀、布”就是典型的静态博弈。第二种依次选择的博弈称之为“动态博弈”(DynamicGames),它的特征是博弈双方的策略选择以及行动不仅有先后次序之分，而且后选择方可以在选择前了解到对手的选择。动态博弈与静态博弈有很大的不同。

在乒乓球战术博弈中，博弈双方运动员依次作出选择，而且是不止一次地作出选择。因此，乒乓球的战术行为博弈是典型的动态博弈过程，它是博弈双方运动员依次轮流击球，在战术博弈中，双方队员不仅有一次策略选择的机会，而且有很多次。在任何一方策略选择之前都对之前的博弈过程完全清楚。

3.4 博弈过程中的获益(Payoffs)

在博弈过程中，博弈双方作出策略选择之后应该有一个能够表示该策略组合下博弈双方的结果。我们对各项策略进行量化后，其博弈的结果也应该是一个量化的数量关系，这种量化数值称之为获益。获益是建立和分析博弈模型的标准和基础，参赛的双方运动员从博弈中所获得的收益，它是所有博弈方唯一的目标，也是运动员进行战术策略行为选择和判断的主要依据。

在经济学领域和其他领域，获益的抽象量化工作应该是利润、收入，或者是量化的效用、社会效益、福利等等。鉴于获益的重要性，实证研究的体育博弈也在尝试抽象量化获益，通常的做法是将一分球或一局球(通常是一分球)的得失作为博弈双方运动员的获益。但是这样做有一个无法解决的问题。乒乓球战术博弈过程是动态博弈，是依次选择的多次行为，其第1板和第3板有直接的关联，但是和第5板、第7板乃至最后的得分或失分就没有多大的关联了，如图2。这样处理有一定的说服力，但是关联度太低，说服力不强。获益量化没有得到很好地解决，其模型的适用性也会大打折扣。

图2 次序博弈的关联性

不同博弈的获益会有不同的特点，而且博弈双方总体获益的差异会导致参与博弈者行为策略选择的不同方式，进而影响博弈的结果，并且再反过来影响参与博弈者的获益。在双人博弈中，博弈双方在一定的策略组合下都有相应地获益。一般的做法是把双方的获益相加而得出所有博弈方获益的总和。在很多博弈中，由于策略组合的不同，总获益也会有所不同。如果这个总获益在任何情况下始终为零，称之为“零和博弈”(Zero-sum Games)；如果总获益始终为一个非零常数，称之为“常和博弈”(Constant-sum Games)；不符合这两种特征的称为“变和博弈”(Variable-sum Games)。

目前较为流行的观点是，乒乓球战术博弈是一种严格意义上的零和博弈，因为一方的胜利就意味着另一方的失败，一方的得分就说明另一方的失分。从一场球、一局球乃至一分球的角度来看待乒乓球战术博弈，它确实是一种零和博弈。但是，从一板球的角度来看问题，我们就会遇到图2次序博弈中关联性的难题，因为考察的这一次击球和对方回球博弈双方运动员所选择的策略，这一板有效击球如果未获得分，它只是为继续击球创造了机会，本方的获益并未对应对方的失利。所以，从一板球的角度来看，乒乓球的战术博弈过程并非是严格意义上的零和博弈，而是一种变和博弈。因此我们要转变观念，重新思考乒乓球战术博弈的获益量化问题。

3.5 博弈过程中的均衡(Equilibrium)

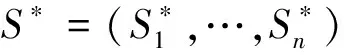
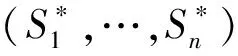
纳什均衡能够使博弈模型得到一个完美、稳定的结果，其重要因素是“一致预测性”，它是指当双方运动员均预测到了一个特定的博弈结果会出现，这个结果能使双方的利益都最大化，因此不会轻易偏离这个结果，当进行战术策略选择时，就具有的稳定性。这里的“一致性”是指双方运动员战术策略的选择与自己的预测一致，不是指双方运动员的预测一致。

在战术行为的博弈分析中一致预测性具有支配性地位，除了纳什均衡其它非纳什均衡的预测都缺乏一致预测[13]，因而决定了纳什均衡在博弈分析中的特殊地位，是纳什均衡的价值体现。

为什么纳什均衡具有这种属性？我们可以设想，如果博弈双方运动员预测到了一个博弈结果(Outcome)，这个结果是一个纳什均衡点，这个纳什均衡点的策略组合是双方的最佳对策，轻易改变自己的策略将会导致本方的获益降低。因此，博弈双方运动员均会坚持自己预测的策略选择，进而获得了与预测相同的博弈结果。所以一致预测性是纳什均衡的本质属性。

这一本质属性使得纳什均衡在乒乓球的战术博弈分析中具有不可替代的重要作用。战术行为预测是博弈分析的最根本目标，研究乒乓球战术行为策略最重要的目的就是预测在激烈的比赛中博弈双方运动员究竟会选择什么样的策略，博弈的结果会怎样，因而纳什均衡是行之有效的工具。不过，在求解纳什均衡时要注意，虽然纳什均衡具有一致预测性，但是纳什均衡的一致预测性是指相同的预测是前提而非结果，并不保证博弈双方运动员的预测相同，因此纳什均衡的分析方法并不一定对所有博弈的结果均能够准确预测。

4 动态博弈的过程和博弈矩阵的构建

传统的比赛分析基本上还停留在技、战术表层指标的水平上，绝大多数为录像观察结合百分率统计。多媒体技术分析虽然能够清晰、形象地演示运动员在比赛中的技战术过程和特点，但都未涉及到统计指标数据之间的动态关系，更少有涉及到动态中的战术思维、策略谋划等深层问题[14]。我们可以把博弈论看作一个分析工具包，它被设计用来帮助我们理解所观察到的运动员决策时相互作用的现象。博弈是对运动员策略相互作用的描述，解是对博弈结果的描述。

在动态博弈中，不同博弈方的选择行为是依次选择，具有先后之分，后选择的博弈方能看到对手的选择行为，因而动态博弈中博弈双方运动员的地位是不对称的。从这点上看，动态博弈与一次性同时选择的静态博弈明显不同。比赛中运动员1分的博弈应该是由若干子博弈组成的，子博弈(Subgame)是动态博弈中满足一定要求的局部所构成的次级博弈。

静态博弈的纳什均衡分析并不能直接套用到动态博弈中，纳什均衡在动态博弈分析中会失效。我们可以引入子博弈完美纳什均衡，它是贝叶斯均衡在完全且完美信息动态博弈中的特例。

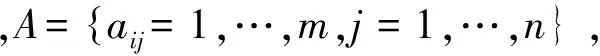
4.1 动态博弈中的子博弈

在乒乓球比赛中，双方运动员是交替击球，符合动态博弈中的依次策略选择，与静态博弈不同的是博弈双方运动员先后选择战术行为策略，而没有同时进行选择。这种博弈与静态博弈的分析方法有一定的差异，在这个动态博弈过程中，运动员在了解对方采用何种战术行为后，根据击球顺序选择本方的战术策略行为。由于这种先后顺序，相比静态博弈，动态博弈呈现出非对称的特性，后选择的一方运动员有较多的信息来帮助本方选择策略，在一定程度上可以减少盲目性。但是，在双人博弈的模型中，获得信息较多的博弈方并不一定能获得更多的利益。

在乒乓球动态博弈过程中，可将这个过程划分为很多个子博弈，这些子博弈是一种次级博弈，它满足动态博弈过程中一定的条件。

定义二：由一个动态博弈所组成的某阶段开始的后续博弈，有初始信息集合进行博弈所需要的所有信息，并且能够组成一个新博弈，这个新博弈属于原博弈的一部分，称之为子博弈[13]。

很显然，在乒乓球比赛中动态博弈由若干个子博弈所构成，如图3。

图3 基于乒乓球速度动态博弈的子博弈构成

在子博弈的分析中，居于核心地位的是子博弈完美纳什均衡。

定义三：在乒乓球战术行为策略选择的动态博弈中，博弈双方运动员选择的策略构成的一个或一组策略组合满足以下条件，在全部动态博弈树中以及所有子博弈分支中均构成了纳什均衡，我们将其称为该动态博弈的“子博弈完美纳什均衡”[13]。

子博弈完美纳什均衡本身也就是纳什均衡，它比纳什均衡稳定性更强，是动态博弈分析最核心的概念和基本着眼点。如图3所示，各分支子博弈的纳什均衡均能构成动态博弈树的纳什均衡。因此，在乒乓球比赛中对博弈双方运动员各分支子博弈(即每1次击球)纳什均衡的求解能够获取每1分球的动态博弈纳什均衡，而运动员分支子博弈具体来说就是每1板球。

4.2 博弈矩阵的构建

目前，在研究乒乓球战术的文献中经常使用“1-3-5拍”“2-4-6拍”这样的叙述，说明乒乓球每一板球之间的关系，1-2、3-4拍是竞争关系，1-3、2-4拍是链接关系。在乒乓球比赛中战术行为可划分为发球、接发球、进攻、防守、相持及得分等。博弈双方运动员依次对战术行为策略做出选择。所以，在比赛中的一个回合能这样描述：博弈方Ⅰ第1板(发球)→博弈方Ⅱ第2板(接发球)→博弈方Ⅰ进攻(失误)→博弈方Ⅱ得分。

张辉提出了马尔可夫性的概念，描述了每一板球所对应的战术行为策略的关系。马尔可夫性是指过程或系统在时刻t0所处的状态为已知的条件下，过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前所处的状态无关。通俗地说，比赛中的下一个战术行为状态仅和现在的战术行为状态相关，而与其上一个战术行为状态无关[2]。

“1-3-5拍”“2-4-6拍”的思维模式给我们提供了乒乓球战术行为动态博弈过程中获益量化的很好地启示。如图4，在有后续击球的情况下，我们并不考虑第n板球与得分或失分的关系，而是考察1-3板、3-5板…、2-4板、4-6板…的直接关联性。也就是说，当有第3板球，就说明第1板球击球有效且有所获益，是第1板击球策略获益的一部分，以此类推。这样所量化的获益就克服了图2中出现的难题。

图4 战术行为的马尔可夫性

举例来说，博弈方Ⅰ是发球方，那么博弈方Ⅰ第1板选择战术策略的获益就是博弈方Ⅱ第2板的失误与博弈方Ⅰ第3板成功击球之和；同理，博弈方Ⅱ第2板选择战术策略的获益就是博弈方Ⅰ第3板的失误与博弈方Ⅱ第4板成功击球之和。那么，推广到任意拍数，计算博弈双方运动员第X板和第X+1板战术博弈的获益由表4的矩阵来表示。

表4 战术行为策略选择的博弈矩阵

5 研究结论

乒乓球运动从一板球的角度来看并非零和博弈，而是一种变和博弈，建立了乒乓球博弈双方运动员战术行为选择的策略库集S，并在子博弈的基础上构建了战术行为策略选择的博弈矩阵，构建的矩阵是进一步量化研究并获得良好博弈模型的基础。

[1] 虞丽娟,张辉,戴金彪,等.隔网对抗项目比赛技战术分析的理论与方法[J].上海体育学院学报,2007,31(3):48-53.

[2] 张辉,霍赫曼·安德烈亚斯.球类比赛数学模拟竞技诊断的理论与实践——以乒乓球比赛分析为例[J].体育科学,2005,25(8):39-44.

[3] 刘文明,唐建军.乒乓球战术行为博弈分析的理论体系建构[J].浙江体育科学,2012,34(6):15-20.

[4] 陈钦,兰伟强.博弈论在高校篮球教学中的实践研究[J].河南教育学院学报(自然科学版),2011,20(4):78-80.

[5] 罗智波,陈旸,陈文胜.论博弈论在体育比赛中的运用[J].湖北体育科技,2004,23(4):433-435.

[6] 张海斌.排球比赛战术的博弈分析[D].北京：中国石油大学,2011.

[7] 孟阳,巫寿生.博弈论在网球发球策略中的应用[J].福建金融管理干部学院学报,2006(2):62-64.

[8] 何志斌.篮球运动实践中的博弈现象个案研究[D].北京：北京体育大学,2007.

[9] 张晓昌.浅析羽毛球发球策略中的混合战略纳什均衡[J].内江科技,2010(2):18-18.

[10] 徐治道.博弈论的基本内容及其发展取向[J].江苏经济探讨,1996(5):38-41.

[11] 唐建军.乒乓球战术体系：技术动作的战术形成及其运用模式[J].北京体育大学学报,2009,32(4):105-107.

[12] 张晓蓬.中国乒乓球队战术训练水平定量诊断方法及实践效用[D].北京：北京体育大学,2004.

[13] 谢识予.经济博弈论[M].上海:复旦大学出版社,2002.

[14] 陈家鸣.乒乓球比赛战术的博弈分析[D].北京：北京体育大学,2008.

(编辑 李新)

Construction of Strategy Selection Game Matrix of Table Tennis Tactical Behavior

YUE Haipeng

Competitive sports require not only strong physical fitness and stable psychology, but also amount of tactical information. The tactical behavior strategy refers to tactically significant series of action or action combinations which have a certain tactical purpose; the construction of table tennis tactical game matrix is the necessary means to further quantitative analysis on athletes’ strategy choice. The study found that table tennis game, when examined from the perspective of one board attack, is not a zero-sum game, but a kind of variable-sum game; it establishes a strategy base set S of table tennis players’ tactical behavior selection, and constructs a tactical behavior strategy selection game matrix based on a sub game; the matrix is a foundation for further quantitative research and a good game model.

tabletennis;tacticaltame;strategyselection;gamematrix

G846 Document code：A Article ID：1001-9154(2017)02-0072-07

岳海鹏，博士，副教授，研究方向：小球训练理论与方法，E-mail：cdtyyhp@qq.com。

成都体育学院,四川 成都 610041 Chengdu Sport University, Chengdu Sichuan 610041

2016-09-13

2017-02-10

G846

A

1001-9154(2017)02-0072-07