冲积河流平滩面积调整模拟计算方法研究

于新荣陶西勇李凌云

（1.慈利县零溪镇水利管理站张家界市427200；2.慈利县岩泊渡镇水利管理站张家界市427200；3.长江科学院河流研究所武汉市430010）

冲积河流平滩面积调整模拟计算方法研究

于新荣1陶西勇2李凌云3

（1.慈利县零溪镇水利管理站张家界市427200；2.慈利县岩泊渡镇水利管理站张家界市427200；3.长江科学院河流研究所武汉市430010）

冲积河流水位达到新生河漫滩时的过流断面面积称为平滩面积，平滩面积调整对河道防洪、航运、水资源利用等多方面存在重要影响。文章基于河道冲淤变形基本方程和不平衡输沙方程，推导建立了冲积河流河道平滩面积调整变化模拟计算方法。方法从理论上阐明了冲积河流平滩面积随水沙条件变化的调整机理，揭示了不平衡输沙是冲积河流河道断面调整的根本原因。利用黄河下游高村站1960～2002年实测水沙资料对模拟计算方法进行了检验，结果表明所提出的方法能够较好模拟出河道平滩面积的调整过程。研究成果有利于准确把握冲积河流断面调整规律，可为相关河道治理与开发提供技术支持。

冲积河流平滩面积水沙条件不平衡输沙

平滩面积是指水位达到新生河漫滩时的过水断面面积，是研究河床演变的重要参数，也是河道主槽修复的重要指标。前人围绕实际地形条件下平滩面积的确定、平滩面积的作用以及平滩面积与各种河流参数之间的定量关系等问题进行了大量研究，为认识河道主槽断面的调整规律，以及开展河道整治和修复河道的输水输沙功能提供了基础。然而由于河床演变本身是一个很复杂的过程，以往大量的研究成果也以经验性的总结为主，缺乏理论基础，计算方法物理意义不明确，给人们深入认识水沙条件变化与河道主槽调整之间的内在联系带来了很大的困难。本文从河床冲淤变形基本方程和不平衡输沙方程出发，建立冲积河流的平滩面积计算方法，为从理论上阐明平滩面积的调整机理提供了基础。

1 基本模型

对于冲积河流，河床变形通过挟沙水流的冲淤来实现。当河流没有水沙量侧向汇入时，一维河床冲淤变形的连续方程如下[1]：

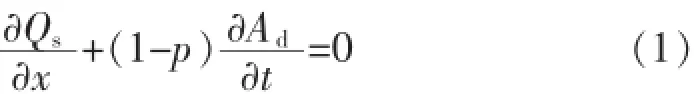
式中Qs——输沙率；

Ad（Ad〉0河道淤积，Ad〈0河道冲刷）——冲淤面积；

p——淤积物空隙率；

x——沿程水平距离；

t——时间。

通常河道平滩面积Ab的调整体现在河道冲淤面积Ad的变化，在不漫滩的情况下，二者有如下关系：

式（2）代入式（1）可得：

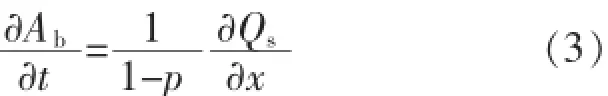
式（3）右端项展开：

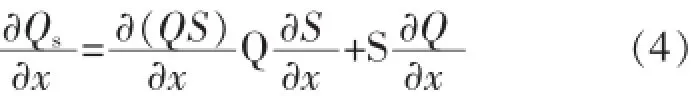
式中

Q——流量；

S——断面平均含沙量。

假定来水来沙条件不变，则沿程流量不变，因此式（4）右端最后一项中∂Q/∂x为零。为计算方便，暂假设河道床沙为均匀沙，根据韩其为的不平衡输沙方程，均匀沙条件下不平衡输沙时平均含沙量沿程变化基本方程如下[2]：

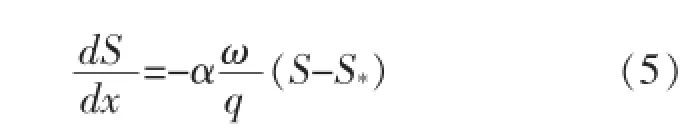
式中

S*——水流挟沙力；

α——含沙量沿程恢复饱和系数；

ω——泥沙颗粒在水中的沉速；

q——单宽流量。

式（5）改写为偏导形式，并与式（4）一起代入式（3）可得：

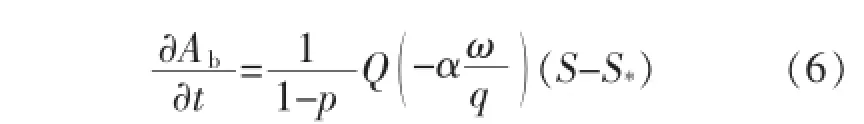
式（6）仅涉及对时间的求导，可将偏导数直接改写为全导数的形式。假设水面宽为B，化简可得：

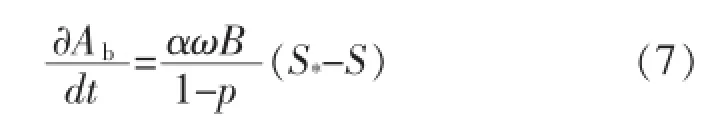
式（7）即为河道平滩面积调整的基本方程。从中可以看出，平滩面积调整的根本原因是河道不平衡输沙，即来水含沙量与水流挟沙力不相等，河道平滩面积的调整通过河道冲淤变形来实现。式（7）揭示了来水来沙条件与平滩面积调整之间的相互作用过程。

2 实用模型

式（7）给出了平滩面积调整的基本方程，但方程中包含有水流挟沙力S*项，基于两方面的原因需要对S*项进行处理：一是常见的水流挟沙力公式使用不方便。常用的挟沙力公式一般涉及到流速、沉速或者粒径等，但这方面的资料往往比较缺乏；二是水流挟沙力的概念一般基于较短的时间尺度而言，一般为几天几个小时甚至几分几秒，关注的是较短时间内水流的挟沙能力，体现短时间内的河道主槽的冲淤情况，而这里我们考虑的是河道主槽在一定水沙条件下长时间作用后的调整情况，关注的时间尺度一般为几个月或者一年甚至更长时间。基于以上原因，下面对式（7）的计算进行变换。

当给定了上游来水来沙条件时，河道会通过冲淤的形式进行调整，调整的结果是使河道含沙量S向水流挟沙力S*靠近，最终河道平滩面积由Ab调整至Ae时达到平衡状态，此时含沙量S与水流挟沙力S*相等。因此可以将S*看成是Ae对应的某种特性，而S看成是Ab对应的某种特性。为方便计算做如下假定：

式中k、k*为系数，式（8）代入式（7）得：

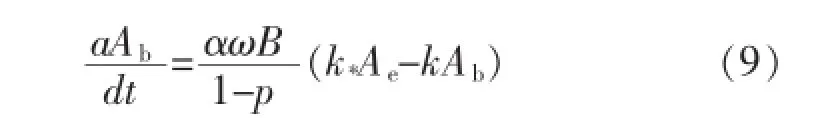
采用近似k=k，*其值大小与水面宽、含沙量恢复饱和系数以及空隙率等因素有关，实际计算过程中可根据实测资料率定。代入式（9）简化为：

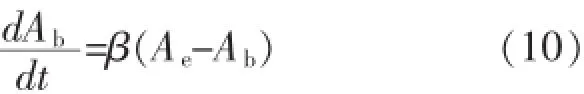
可以看到，式（10）与吴保生所建立的平滩面积滞后响应模型具有相同的形式[3]。不同的是平滩面积滞后响应模型是基于冲积河流具有自动调整的原理，其调整速率与当前状态同平衡状态之间差值成正比的假设得出，而本文是基于河床冲淤变形基本方程和不平衡输沙方程推导得到，其理论基础相对较强，这也正是以往常用的计算方法所缺乏的。

当来水来沙条件确定时，平滩面积平衡值Ae即为一定值。因此式（10）有以下形式的通解（负指数衰减函数）：

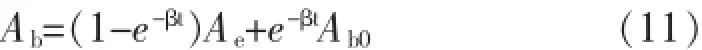
其中Ab0为t=0时的平滩面积。吴保生的研究表明，平滩面积的调整与来水来沙条件密切相关，平滩面积平衡值Ae可采用如下方程计算[4]：

式中

Qf——汛期平均流量；

ξf——汛期平均来沙系数，其值为汛期平均含沙量与汛期平均流量之比。

k、b和c——待定系数和指数，根据实测资料率定。

将式（12）代入式（11）得：

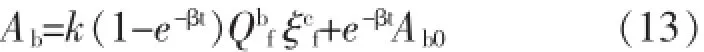
式（13）即为实用的平滩面积计算模型。

3 模型应用

黄河下游是典型冲积河段，其河道断面形态随水沙条件频繁剧烈变化。本文收集了黄河下游高村水文站1960～2002年系列水沙及平滩面积资料，根据这些水沙资料，率定式（13）中的相关参数，可得k=6.6，b=0.171，c=－1.075，β=0.213，代入式（13）得：

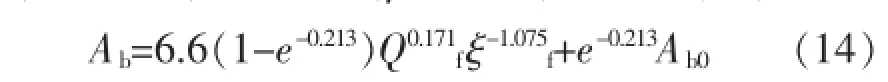
式（14）计算结果如附图所示。计算值与实测值符合很好，相关系数R2=0.90。从附图可以看出，利用该方法模拟计算高村站的平滩面积，计算值与实测值历年变化过程基本一致，说明该方法能够真实反映平滩面积随水沙条件的调整规律。

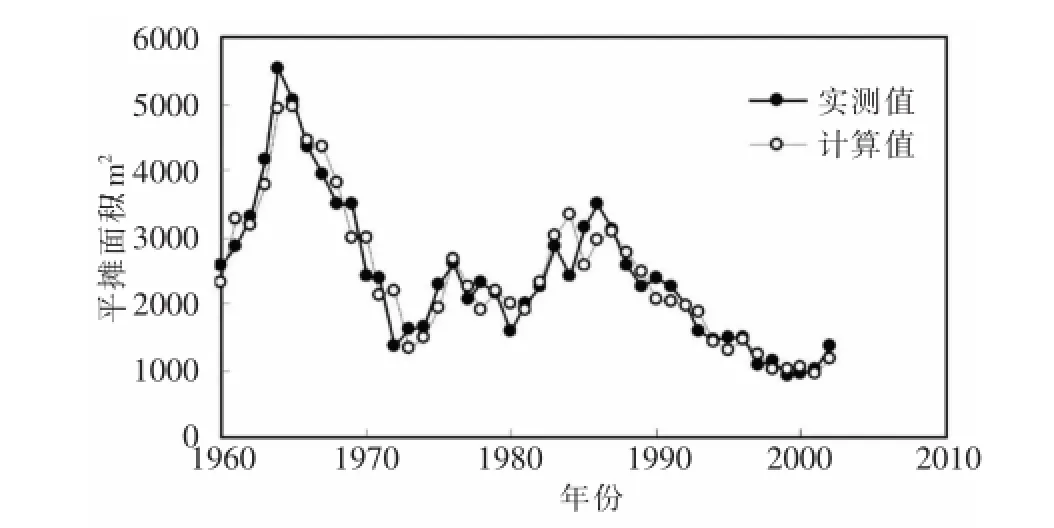
附图式（14）计算高村站平滩面积与实测值对比

同时我们也看到，有些年份计算值与实测值变化趋势不一致的情况，分析原因是原模型是基于不漫滩的情况下推导得出。当洪水不漫滩时，河道若发生淤积，则淤积全部集中在主槽，主槽断面减小，式（2）即反映了这种情况；当洪水出现漫滩时，河道发生淤积，其中部分淤积量将分布在滩地，这部分淤积量不仅不会使主槽断面面积减小，反而有可能因抬高了滩唇高程使主槽断面面积扩大，这与式（2）反映的情况不一致。因此下一步的研究可在考虑漫滩的情况下对模型进行改进。

4 结论

本文从河道冲淤变形基本方程和不平衡输沙方程，推导出了平滩面积调整模拟计算方法，并利用黄河下游高村站水文站1960～2002年的水沙实测资料进行了验证。主要结论如下：

（1）推导建立了具有一定理论基础的平滩面积计算方法式（13），方法反映了来水来沙条件同河道平滩面积调整之间的内在联系。

（2）利用黄河下游高村水文站1960～2002年实测水沙资料验证表明，式（13）能够很好地描述河道平滩面积的调整规律。

[1]钱宁，张仁，周志德.河床演变学[M].北京：科学出版社，1987.

[2]韩其为.水库淤积[M].北京：科学出版社，2003.

[3]Wu B S,Xia J Q,Fu X D,et al.Effect of altered flow regime on bankfull area of the Lower Yellow River,China[J].Earth Surface Processes and Landforms,2008,33（10）：1585－1601.

[4]吴保生.冲积河流平滩流量的滞后响应模型[J].水利学报，2008，39（6）：680－687.

2016－07－20）

于新荣（1980－），女，湖南慈利人，大学本科，工程师，现在慈利县零溪镇水利管理站工作，联系电话：0744－3223633；陶西勇（1976－），男，湖南慈利人，大学本科，工程师，现在慈利县岩泊渡镇水利管理站工作，联系电话：0744－3510006；李凌云（1982－），男，湖南慈利人，博士，高级工程师，主要从事水力学及河流动力学相关研究工作，联系电话：027－82926172。