基于网络搜索数据的福州市商品房价格指数预测模型研究

庄虹莉，李立婷，林雨婷，刘艺辉，温永仙

（福建农林大学 计算机与信息学院，福建 福州 350002）

基于网络搜索数据的福州市商品房价格指数预测模型研究

庄虹莉，李立婷，林雨婷，刘艺辉，温永仙

（福建农林大学 计算机与信息学院，福建 福州 350002）

文章以百度搜索引擎上的关键词指数为数据基础，首先通过指标平稳性检验与时差相关性分析从初始关键词库中选取出14个关键词作为解释变量指标，其次建立基于惩罚函数的变量选择（Elastic N et、SCA D和G roup Bridge）对福州市商品房价格指数进行预测，再者基于四种不同误差指标，运用综合评判分析法对惩罚函数的变量选择、多元线性回归分析、偏最小二乘回归分析、随机森林的预测精度进行综合分析，最终确定G roup Bridge为福州市商品房价格指数的最佳预测模型。

随机森林；Elastic N et；SCA D；G roup Bridge；综合评判分析法

一、引言

随着互联网的飞速发展，大数据时代降临，人们获取信息的渠道变得更加宽广，尤其是搜索引擎在人们生活中扮演者不可或缺的角色。房地产交易过程也不例外，人们通过搜索引擎了解最新的经济形势与政策，从而做出合理的消费决策，所以说搜索引擎在消费者、开发商以及政府中起到桥梁性作用。所以基于网络搜索数据对福州市的商品房价格指数进行预测模型分析具有一定的研究价值。通过建立一系列合理的模型对网络搜索数据进行深入分析，最终得到预测福州市商品房同比价格指数的最优模型，实现在一定程度上对商品房同比价格指数的预测，解决房价相关信息的时滞性问题，同时也为相关部门的调控工作提供理论支持。

目前国内学者基于网络搜索数据（主要是百度指数）在房地产价格、商品零售价格等领域都有所研究，主要研究方法以定量分析为主。例如董倩[1]等就是基于百度指数对北京等16大中城市的新房价格与二手房价格建立6种预测模型（线性回归、随机森林等），得到各城市房价的最优预测模型；姜文杰[2]等就是基于百度指数对我国大中城市分别建立ARMA模型与自回归分布滞后模型，然后比较两种模型的预测效果，解决房价相关信息的时滞性问题；刘伟江[3]等就是基于谷歌指数采用时差相关分析方法选取与商品价格相关性较高的关键词，然后再利用回归模型进行价格指数预测。

最早利用网络搜索数据资源开拓全新的研究领域是美国的 Ginsberg J[4]，他们团队利用 Google搜索指数成功预测流感发展趋势，大致估计流感的定期发病率；接着是 Askita与Zimmermann[5]同样基于网络搜索数据成功预测出失业率的变化趋势等。

本文基于惩罚函数的变量选择对网络搜索数据进行深入的研究，借助四种不同的误差指标与传统的预测模型进行对比，最终得到预测福州市商品房同比价格指数的最优模型。

二、惩罚函数的变量选择

回归是传统的预测模型，即通过得到解释变量的参数估计实现预测，而惩罚函数的变量选择既能实现参数估计又能实现变量选择，即既能实现预测又能降低模型的复杂度。

对于线性回归模型：

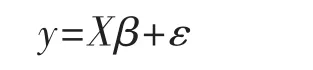
其中ε～N（0，σ2）的随机误差项，β是回归系数，y为连续的响应变量。传统的对线性回归模型的参数估计是最小二乘，则β的最小二乘估计为：

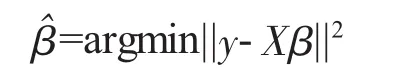
但是最小二乘估计也存在不足之处：

（1）对于高维数据（n＜p）或当解释变量存在多重共线性时，难以实现对β的估计。

（2）最小二乘无法实现变量选择，这将导致模型过于复杂。

惩罚函数的变量选择思想在于：在最小二乘或极大似然函数的基础上加入惩罚函数项得到新的目标函数，然后通过最小化或者最大化目标函数得到参数估计值。其实就是将不显著变量的系数压缩为零而把该变量剔除，对显著变量进行很小或不压缩而保留在模型中，最终实现模型的变量选择和参数估计。

在最小二乘估计的基础上引入不同的惩罚项，就可以得到不同的惩罚函数变量选择方法。这里选择代表性的几个惩罚方法进行研究：单变量选择方法（SCAD）、高度相关数据的变量选择（Elastic Net）和双层变量选择方法（Group Bridge）。

1.SCAD。SCAD是实现单变量的选择方法，由Fan和Li[6]在Lasso基础上发展的一种非凹的惩罚函数，其定义如下：

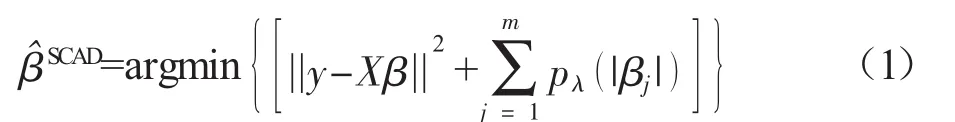
其中，pλ（|βj| ）是SCAD惩罚项，定义如下：

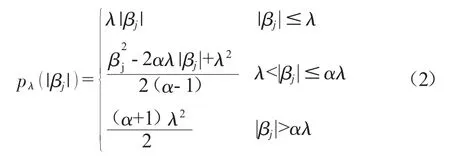
其中，α＞2为调整参数，λ＞0为罚参数。Fan指出α=3.7时，其估计效果最好。

SCAD惩罚会把与被解释变量不相关的解释变量所对应的系数压缩为0，其他一些变量系数朝0压缩，当变量系数很大时则基本保持不变，使得最后得到的估计量满足：无偏性、稀疏性和连续性，连续性使得结果更为稳定。

2.Elastic Net。Elastic Net是Zhou和Hastic[7]在岭回归和Lasso的基础上提出的新的变量选择方法，是处理高维高度相关数据的变量选择方法，解释变量间通常具有群组效应，即高度相关的预测变量的系数应该相等或是接近相等。其定义如下：

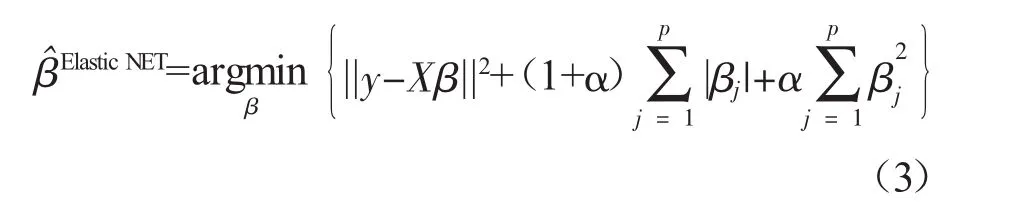
（3）式是岭回归惩罚项和Lasso惩罚项的一个凸组合。其中α为罚参数，当α=0时，上式为Lasso回归；当α=1时，上式为岭回归。因此Elastic Net回归结合了岭回归和Lasso回归的优点，既能消除变量间的多重共线性，又能进行变量选择，还能处理群组效应。

3.Group Bridge。双层变量选择方法的独特之处：筛选变量时考虑了变量的分组情况，不仅能够筛选出重要分组，而且能够在组内筛选出重要的单个变量。Huang等[8]提出双层变量选择可以看成是组内惩罚和组间惩罚的一种复合函数，即对第j组变量的惩罚项表示为：

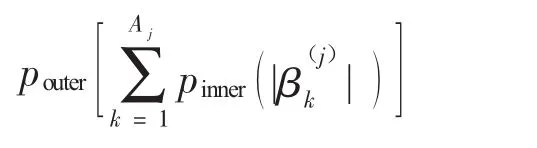
其中，pouter是组间惩罚，pinner为组内惩罚。

Breheny和Huang提出，只需在组内和组间都选择实现单个变量选择的惩罚函数，例如Lasso、SCAD、MCP惩罚等，就能实现组间和组内的变量选择[9]。由此得到了Group Bridge[9]变量选择方法，它是组内进行Lasso惩罚，组间进行Bridge惩罚。

Group Bridge变量选择方法的基本定义为：假设已知分有J组变量，分别为A1，A2，…，AJ，令βAJ=（βj）j∈Aj为 β相应变量构成的子向量，则 Group Bridge的定义如下：

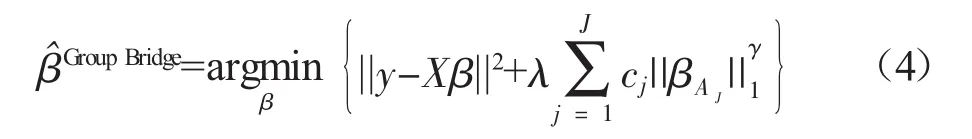
其中，λ＞0是罚参数，常数cj为βAJ的调整参数，一般选择 cj∝|Aj|1-γ，γ为 Bridge的指标，当 0＜γ＜1时，式（4）可同时实现单变量和组变量的选择。

4.罚参数的选择。惩罚函数的变量选择中罚参数对模型的精度至关重要，合适的罚参数能够有效的提高预测精度和降低模型的复杂度。本文通过10折交叉验证[10]（10-fold Cross-Validation）实现罚参数的选择。

三、福州市商品房价格指数预测模型的实证分析

本文通过基于惩罚函数的变量选择对网络搜索数据进行深入的研究，借助四种不同的误差指标与传统的预测模型进行对比，最后通过综合评判得到预测福州市商品房同比价格指数的最优模型。

（一）数据准备

1.研究对象

由于福州市实属二线城市，属于经济水平较高、房地产交易活动相对活跃的地级市省会，购房者对于房地产信息的收集渠道主要还是以网络搜索为主（在我国主要以百度搜索引擎为主），搜索引擎上的关键词指数体现了购房者的关注点，所以本文基于网络搜索数据前提下对福州市的商品房价格的预测分析具有一定的价值性与实用性。

2.数据来源

本文的研究对象之一：福州市的商品房价格指数数据来源于国家统计局（http：//www.stats.gov. cn/）每个月所公布的关于“70个大中城市住宅销售价格变动情况”的报告内容。本文主要搜集福州市从2012年1月至2015年12月总计48个月的新建商品住宅月度价格指数（包括环比指数、同比指数、定基指数，本文主要对同比价格指数进行研究）。

本文的另一研究对象：关键词搜索量数据主要来源于百度指数（http：//index.baidu.com/），百度搜索指数能综合反映该关键词在过去一天用户与媒体对其的关注度，是以海量网民的搜索数据为基础的数据分享平台，主要的功能模块可分为：趋势研究、需求图谱、舆情管家、人群画像等。本文主要通过趋势研究这一模块（以整体趋势为主）来获取关键词的搜索量（按每日搜索量统计）。

3.数据预处理-初始关键词的选取

（1）从定性方面分析。由图1的理论框架可看出，分别能从主体因素与非主体因素两方面进行关键词的初步选取，从主体因素（房地产市场供求关系、房地产经济交易活动以及与房地产相关联的指标等）分析考虑，最终通过人为选取出“福州房价、福州房地产、户型、建材”这4个作为主体因素的基准关键词；同样从非主体因素（宏观经济形势、与房地产密切相关的调控政策等）分析得到：“房贷利率、公积金、买房政策”3个作为非主体因素的基准关键词。

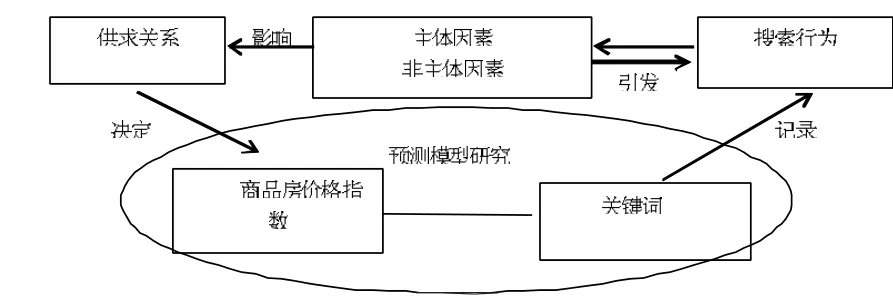
图1 基于网络搜索数据对商品房价格指数预测模型进行研究的理论框架

（2）从定量方面分析。通过以上定性分析得到的7个基准关键词，首先利用百度搜索引擎的关键词推荐技术（其原理是可查询与指定关键词相关度较高的词汇）对基准关键词范围进行适当扩展，得到与7个基准关键词相关的关键词58个，总计65个；接着以百度指数为标准对这65个关键词进一步筛选，将在研究时间范围内数据量相对较少以及出现重复的关键词一一剔除，最后通过定量分析，确定“福州房地产、住房公积金、房贷利率”等48个指标作为初始关键词，构建成一个关键词库。这48个指标的具体变量名见表1。

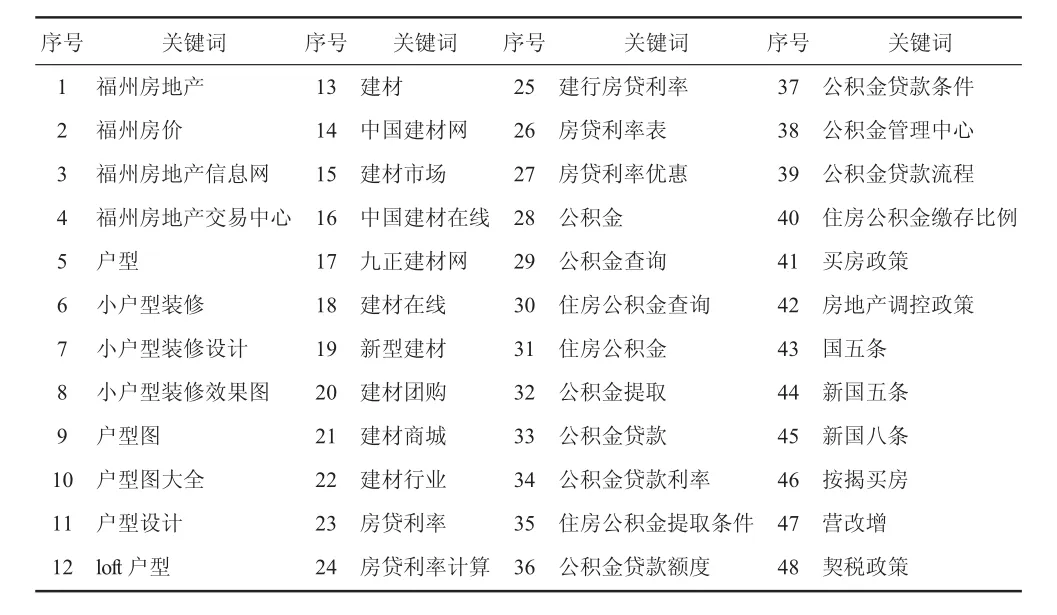
表1 48个指标所对应的关键词

（二）模型准备

由于本文的最终目的是对福州市的商品房价格指数的预测模型进行比较分析，所以从关键词库里的解释变量选取解释变量指标这一环节至关重要，不仅需要考虑与商品房同比价格指数相关度，还需考虑到两者间的时差关系。时差关系主要包括领先、同步与滞后三个阶段，只有与基准指标处于领先或同步的指标才能在预测活动中起到相关作用，具有一定的研究价值。对于时差关系判断本文选择的是时差相关分析法，它可以较完整体现两个变量间的时差性与相关性。而只有平稳时间序列才可以进行时差相关分析，所以在进行时差相关分析之前要进行平稳性检验，对于非平稳序列进行差分处理将其转化为平稳序列。

1.指标选取——平稳性检验[11]。首先将所有变量的时间序列都画出序列图，然后进行ADF检验，而对于非平稳序列进行差分处理，直至使之成为平稳序列。

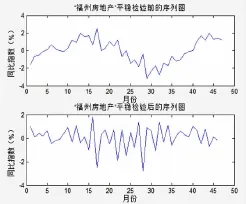
图2“福州房地产”平稳检验前后序列图

具体检验结果为：所有变量的时间序列都是经过二次差分后将其转化为平稳序列。

2.时差相关分析。时差相关分析具体实现公式如下：

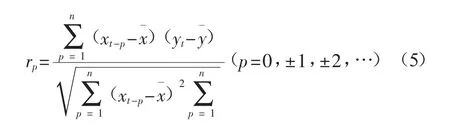
由于本文主要研究对象是福州市商品房同比价格指数，所以将其作为基准指标，其余解释变量作为检验指标，利用SPSS软件实现时差相关分析，在22个领先或同步指标中选取相关系数在0.55以上的变量（14个）作为预测模型中的解释变量，具体如表2所示：

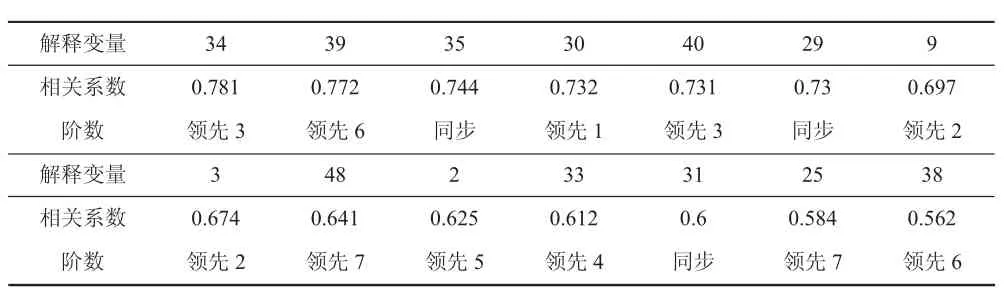
表2 相关系数大于0.55的领先或同步解释变量

经过指标平稳性检验与时差相关分析，最终确定14个解释变量作为以下预测模型中的解释变量指标，其中公积金、房贷利率与政策属于非主体因素，而房价信息与户型属于主体因素，也就是说时差相关分析选取出的指标是具有典型性的，在很大程度上代表了广大购房消费者所关注的方面，所以将这14个指标当成预测模型的解释变量具有客观性与科学性。

在这14个关键词指标中，有将近60%成分是属于公积金这一因素范畴的，结合公积金原始搜索量数据，可直观看出福州市民在购房交易中会把关注点集中在公积金及其相关因素上，接着才是房贷利率、调控政策以及户型这些较为重要的因素上。

（三）惩罚函数的变量选择方法

惩罚函数的变量选择方法是将某些解释变量的系数压缩为0，以牺牲偏差为代价而提高预测精度。因此本文采用惩罚的变量选择方法对这14个解释变量进一步降维。为了评价模型的优劣，将前35个样本作为训练集，后13个样本作为测试集，通过实现对测试集的预测，定量评价模型的优良。

借助R语言的包实现对惩罚函数的变量选择方法的参数估计和变量选择，通过求解得到三种惩罚函数的变量选择的回归方程为：

从三个惩罚函数的变量选择模型的回归方程中，得到公积金贷款利率、住房公积金提取条件、福州房地产信息网，这三个关键词应该是影响福州市商品房价格指数的比较重要的因子，也包含了房地产业交易活动所考虑的大部分综合因素，所以能较全面反映出福州市商品房价格指数变化，说明惩罚函数的变量选择方法在显著变量筛选功能上的效果不错。

为了与其他传统的预测模型进行比较，分别对后13个样本进行预测，预测的结果详见表3。其中多元线性回归、偏最小二乘、随机森林是常用的回归预测模型，前两者是参数估计领域，而随机森林是非参数估计领域且能够实现变量选择，因此采用这三种方法与惩罚函数的变量选择方法进行对比。

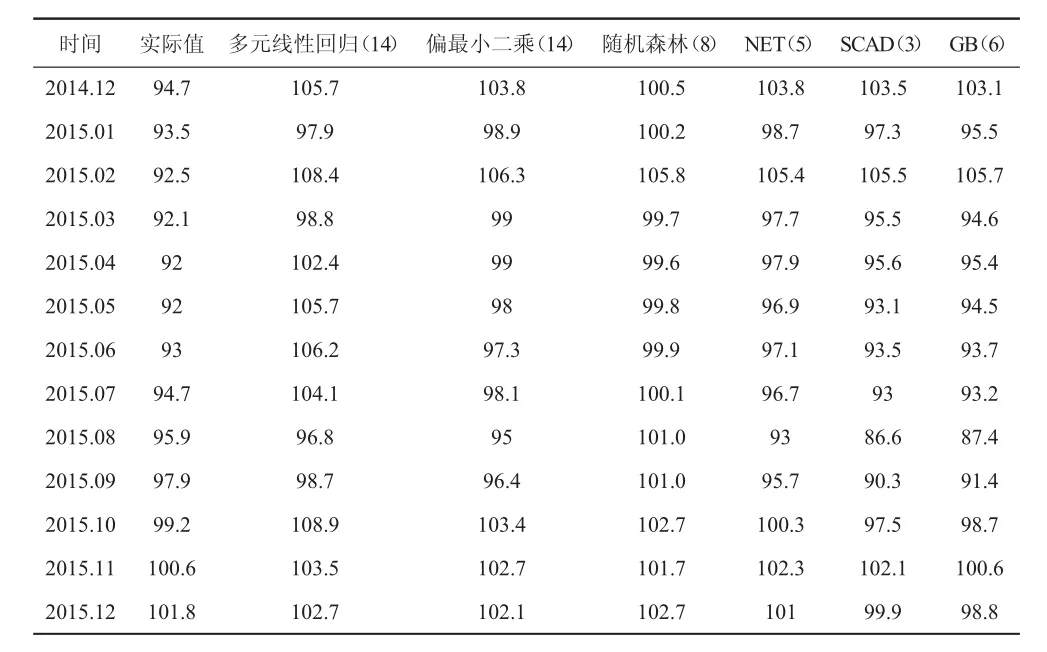
表3 预测结果比较

（四）预测精度综合分析

1.求解误差指标。为了直观的能够从数值上衡量以上六种模型的预测精度与稳定性，本文针对误差进行分析，选用平均绝对误差（MAE）、平均相对误差（MRE）、均方根误差（RMSE）、均方百分比误差（MSPE）这四种误差指标对测试集的预测结果进行评价。分别计算出六种模型的四种误差指标如表4所示。

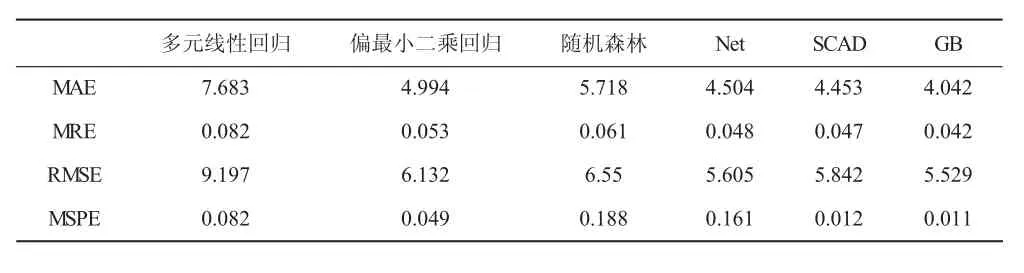
表4 各模型误差指标分析表

通过表4数据可看出惩罚函数的变量选择中的SCAD和GB均表现出优良的性质，四种误差都相对较小，但是为了更加直观的显示出结果，在这里进一步采用基于四种误差指标的综合评判分析法，对这六种模型的拟合度与稳定性进行权衡与评定。

2.综合评判分析法[12]。综合评判法是一种采用多个评价指标对目标方案从定性与定量两个方面进行综合评判的方法。其基本原理是通过对所建立的评价因素进行相关处理得到一些可以反映目标方案优劣性的评价指标，从而得出目标方案的优劣性比较结果。评判结果集里的评价值代表模型的优越性，评价值越大，说明该模型的性能越好。借助MATLAB求解得到综合评判结果集：

C1=[0.174 0.284 0.125 0.151 0.916 0.999]

由综合评判的结果集可得到本次综合评判中各个预测模型的优属度，就从这四个评价指标分析，可较直观看出GB和SCAD模型的预测精度极高，分别为0.999和0.916，远比其他的四种模型大的多，因此将惩罚函数的变量选择方法应用到网络搜索数据，能够得到较高精度的预测模型。由于本文采用的网络搜索数据中的解释变量具有明显的分组，即分成6组（比如将与公积金相关的变量看成一组），因此适用于分组变量选择的GB比单变量选择的SCAD拥有更高的预测精度，而且选用变量数更全。因此将GB作为网络搜索数据福州市商品房价格指数的最佳预测模型。

四、结果综合分析

（一）关键词指标结果分析

首先通过时差相关分析选取的关键词指标有14个，其中有9个（将近60%比例）是属于“公积金”这一因素范畴的，有两个指标是属于“福州房价信息”，“房贷”、“政策”与“户型”分别占有一个指标。而对于多元线性回归分析与偏最小二乘回归两种模型并不能实现变量选择；随机森林通过得到因子的重要性得分能够实现变量的选择；惩罚函数的变量选择方法能够实现变量选择（大幅度的降低模型的复杂度）并实现参数估计，对于Elastic Net选择出的关键词指标总计 4个，其中“公积金”范畴有3个指标，另一个属于“福州房价信息”；SCAD选择出的关键词指标总计3个，其中“公积金”范畴有2个指标，另一个属于“福州房价信息”；Group Bridge选择出的关键词指标总计 6个，其中“公积金”范畴有4个指标，另外属于“福州房价信息”和“契税政策”，涉及更多类型的变量，因此这里的预测精度更高。

通过以上分析，不难发现这六种模型对于关键词指标的选取具有很高的相似度，说明通过不同的预测模型研究可以分析出福州市的购房者对于“公积金”及其相关因素的关注度相当高，对于“福州房价信息”、“房贷”与“政策”这些因素关注度也比较高，而对于“建材”与“户型”对买房因素关注度相对较低。因此通过预测模型中的关键词指标可以直观看出福州市民所关注的方面，政府与相关部门可以从关注点出发，基于最佳预测模型的研究基础，采取合理的措施，维持房地产业健康发展。

（二）预测模型结果分析

1.从预测精度分析。本文对于六种模型的预测精度分析采用的是针对四种误差指标进行综合评判分析，得到Group Bridge的预测精度较高，SCAD次之，均比其他四种模型的精度高得多。

2.从模型复杂度分析。多元线性回归模型与最小二乘回归分析这两种预测模型无法实现变量的选择目标，仅能得到14个因子的参数估计，进一步用于预测；而对于惩罚函数的变量选择就具有显著变量筛选的功能，所以在一定程度上减少了工作量且选取出的解释变量数远比其他两种模型解释变量数量来得少，关键是还能达到一个较好的预测效果。

综上所述，六种模型各有优缺点，针对不同的研究对象，可能适用不同的预测模型。本文综合考虑预测精度、模型复杂度，最终将GB作为预测福州市商品房价格指数的最佳模型。

五、总结

大数据背景下，充分利用网络数据资源挖掘出相关重要信息来分析解决一些实际问题是现在乃至未来的重要研究趋势。本文研究的创新之处在于利用关键词搜索指数对福州市的商品房价格指数进行预测与分析，具体表现为以下几个方面：

其一，本文利用关键词的百度指数这一网络数据资源来反映福州市商品房价格指数的变化趋势，该网络数据资源在一定程度上能较为全面反映购房消费者的即时状态与消费心理，同时网络数据这一虚拟化资源能在购房消费者与房地产业两者间起到桥梁作用，能将两者的此时形势与状态及时传达给对方。所以本文所利用的数据资源能较为全面反映在大数据背景下福州房地产业的交易形势。

其二，本文主要是将惩罚函数的变量选择运用到网络搜索数据，对福州市商品房价指数进行预测，为了评价该方法的好坏，进一步与传统解决网络搜索数据的方法（多元线性回归分析、偏最小二乘回归分析、随机森林）进行对比。

其三，本文所运用的预测精度分析方法-综合评判分析法具有一定的科学性与全面性，从定量方面上较为准确阐释模型的性能优劣，具有较高的可信度。

[1]董倩，孙娜娜，李伟.基于网络搜索数据的房地产价格预测[J].统计研究，2014，31（10）：81-88.

[2]姜文杰，2016.基于百度指数的房地产价格相关性研究[J].统计与决策（2）：90-93.

[3]刘伟江，2014.基于网络关键词搜索量的商品零售价格指数预测研究[J].制度经济学研究（4）：153-169.

[4]Ginsberg J，Mohebbi M H，PateI R s，et a1.Detecting influenza epidemics using search engine Query data[J].Nature，2009，457：1012-1014.

[5]Askitas N.，Zimmermann K.F，Google Econometrics and unemploymentForecasting[C].working Paper，2009：107-120.

[6]Fan J，Li R.Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties[J].Journal of the American Statistical Association，2001，96（456）：1348-1360.

[7]Hui Z，Trevor H.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society，2005，67（2）：301-320.

[8]Huang J，Breheny P，Ma S.A Selective Review of Group Selection in High-Dimensional Models[J].Statistical Science，2012，27（4）：481-499.

[9]Breheny P，Huang J.Penalized methods for bi-level variable selection [J].Statistics and its interface，2009，2（3）：369-380.

[10]高少龙.几种变量选择方法的模拟研究和实证分析[D].山东大学，2014：8-10.

[11]贾杰林，李健，吴舜泽.水环境趋势预警指标体系的构建与时差分析.中国水污染控制战略与政策创新研讨会论文集[C].中国环境科学学会，2010：44-51.

[12]宋俊杰.三峡流域中长期径流预报模型精度评定综合分析及优化方法研究[D].华中科技大学，2013：15-32.

（责任编辑：D 校对：T）

F299.233

A

1004-2768（2017）02-0105-07

2016-11-25

国家自然基金资助项目“禾谷类作物胚乳性状多QTL定位统计方法研究”（31171448）；国家自然基金资助项目“基于高维数据和全基因组标记的数量性状基因定位方法研究”（31571558）；福建农林大学数学建模实训室（111ZS1503）

庄虹莉（1990-），女，福建农林大学计算机与信息学院硕士研究生，研究方向：数理统计及应用；李立婷（1993-），女，福建农林大学计算机与信息学院硕士研究生，研究方向：数理统计及应用；林雨婷（1992-），女，福建农林大学计算机与信息学院硕士研究生，研究方向：数理统计及应用；刘艺辉，男，福建农林大学计算机与信息学院，研究方向：数理统计及应用；温永仙（1966-），女，福建农林大学计算机与信息学院教授，研究方向：数理统计及应用。温永仙为通讯作者。