水土压力的理论分析与释义

摘要：基坑支护中的水土压力计算一直困扰岩土工程界，对于“水土合算”与“水土分算”存在许多争议。根据土的三相组成和土中水的实际存在状态，对土中水进行了分类和解释，同时对饱和土地层进行了分析，提出强结合水、弱结合水、毛细水、自由水与孔隙水的区别。文章阐述了水土压力的理论分析与释义。

关键词：水土压力；结合水；毛细水；自由水；孔隙水；朗肯土压力理论 文献标识码：A

中图分类号：TU44 文章编号：1009-2374（2017）01-0122-03 DOI：10.13535/j.cnki.11-4406/n.2017.01.059

目前地下空间的开发越来越快，工程设计中水土压力的计算力求既简便又精确，既不会造成安全隐患又不致过于浪费。但水土压力计算问题长期困扰岩土工程界，曾经引起很大争论。许多专家、学者致力于水土压力计算方法的研究，并提出自己的观点。

魏汝龙教授提出由于弱渗透性黏性土中，土压力对支护结构的影响在短时间内难以得到体现，以至于有人认为有效应力原理不适用于这类黏土，并论证了用总应力强度指标进行“水土分算”的合理性；杨晓军、龚晓楠认为“水土合算”只是一种经验方法，没有实际的理论依据；王洪新把土的孔隙比、界限含水量、颗粒分析等物理参量引入水土压力计算中，提出一个水压力比率，把有效应力强度指标和总应力强度指标统一在一个强度公式中。并且给出了一个“水土分算”和“水土合算”的算法，实现了两者结果之间的过渡；刘发前提出对于单粒结构而言，“土压力”为土颗粒与所吸附结合水对地下结构物的作用；对于近似于絮状的结构，大部分流体水受到土颗粒的吸引、絮状结构的束缚无法形成流动水，有效降低土压力，水压力大打折扣，这就是黏性土中实测水土压力接近于“水土合算”的原因。

目前大部分专家都认为黏性土中采用“水土合算”，砂性土中采用“水土分算”，与现场实测值较为接近。“水土分算”符合有效应力原理，但是仅在砂性土时与现场实测接近；黏性土采用“水土合算”相当于对水压力进行了折减，不符合有效应力原理。实际上，“水土合算”与“水土分算”存在许多问题没有解决，急需找到一个正确的水土压力计算公式，实现“水土合算”与“水土分算”的统一，并符合有效应力原理，从理论上提供水土压力计算依据。

本文通过对有效应力原理和土的三相释义，提出土中水由强结合水、弱结合水、毛细水或自由水组成，占据土中气相能自由移动的才是孔隙水。按照上述说法可以判断，目前常规的“水土合算”和“水土分算”公式全部是有效应力原理下的“水土分算”，验证了水土压力计算的理论依据。对于黏性土可以理解为由于颗粒间孔隙较小，土中只有强结合水、弱结合水、毛细水或自由水，不会存在孔隙水，因此按孔隙水压力为0计算。解决了存在多年的水土压力计算争议。

1 有效应力原理释义

太沙基从试验中观察到在饱和土体中土的变形及强度与土体中的有效应力密切相关，并建立了有效应力

原理：

σ=σ'+μ

式中：σ为平面上法向总应力，kPa；σ'为平面上有效法向应力，kPa；μ为孔隙水壓力，kPa。

有效应力原理表示研究平面上的总应力、有效应力和孔隙水压力三者之间的关系：当总应力保持不变时，孔隙水压力与有效应力可以相互转化，即孔隙水压力减小等于有效应力的等量增加。

有效应力原理可以解释为饱和土体是由土和土体中的孔隙水组成，孔隙水对土产生浮力，σ'（平面上的有效法向应力）实际上是土的重力减去土所受的浮力对平面产生的有效应力，μ（孔隙水压力）是由于孔隙水是连通的，饱和土体中的孔隙水对平面产生的孔隙水压力。有效应力原理可以解释城市水位下降土体下沉现象：当城市水位下降，原饱和土中孔隙水下移，变为非饱和土体。非饱和土体孔隙中无孔隙水，土体所受浮力为零，土体的重力变为有效重力，有效重力比饱和土体时浮重力增大，上层土体对下层土体有效重力增大，有效应力增加，下层土被压密实，导致土体下沉。

2 土的三相组成和释义

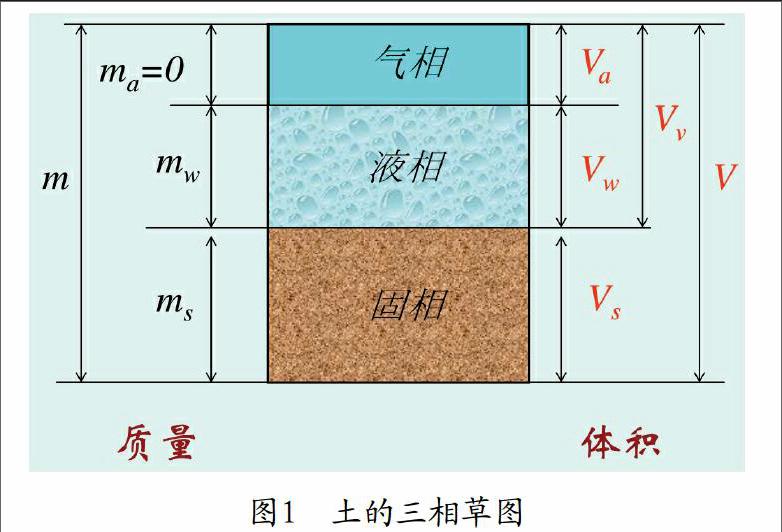
土是由固相（土体颗粒）、液相（水）和气相（不饱和情况下的气体）组成，土的三个比例不同其性质不同。为了研究方便，将本来交错分布的三相分别集中起来，按体积和质量的比例画出图来（如图1）。土中土颗粒、水、气的质量分别为ms、mw、ma，体积分别为vs、vw、va，总质量为m，总体积为v。土中水由于含量不同可以分为强结合水、弱结合水、毛细水和自由水。当水存在于最靠近土颗粒表面处，土粒强电场范围内的水分子和阳离子一起吸附在土粒表面而定向排列形成一层薄的水膜，并固定不动，不能传递静水压力，这层水就称为强结合水。水紧靠于强结合水的外围，形成一层水膜，所受电荷引力降低，较厚的水膜可以向邻近较薄的水膜缓慢移动，不能传递静水压力，这层水就称为弱结合水。土中存在一定的孔隙，对于直径较小孔隙由于毛细管现象赋存于孔隙中的水，不传递静水压力，称为毛细水。弱结合水之外的水完全不受土粒电场引力影响，可以自由移动，能够传递静水压力，称为自由水。土中的强结合水、弱结合水、毛细水、自由水的存在，直接造成土的固体状态、半固体状态、可塑状态、流塑状态，土中水的含量直接影响到土的抗剪强度。毛细水是指土处于固体或可塑体，土中孔隙含有毛细管现象的水，此时固体或可塑体中的孔隙存在以下两种可能：（1）孔隙全部被毛细水占据；（2）孔隙一部分被毛细水占据。当土中含有自由水（也就是平常所说的含水量大于液限）时，土已经无气相，呈流塑状态。注意：此处所说的自由水与土颗粒、强结合水、弱结合水是一整体，没有办法将其有效分开，与饱和土体中的孔隙水是不同性质的水。有效应力原理中的饱和土体中的孔隙水实际上是水占据了土中的气相，在土体孔隙中以自由移动的水（不含毛细水），当水位下降或采取降水措施可以与土体完全分开，分开后饱和土变为非饱和土。因此可以理解为土是由土颗粒、强结合水、弱结合水、毛细水、自由水或气体构成。饱和土由土与占据气体体积的孔隙水构成。对于有效应力原理可以理解为土颗粒、强结合水、弱结合水、毛细水或自由水共同作用组成土体形成土的有效应力，存在的孔隙水产生了孔隙水压力。

3 水土压力的理论计算

根据朗肯土压力理论，朗肯主动土压力计算公

式为：

主动土压力计算公式：

σa=σEtan2（45°-φ/2）-2ctan（45°-φ/2）

式中：σa为深度为E处的主动侧向土压力；σE为深度为E处的地层自重应力；c为地层的粘聚力；φ为地层内摩擦角。

根据以上有效应力原理（σ=σ'+μ）释义，深度为E处的地层法向总应力是E处的土有效法向应力和孔隙水压力之和。E处的主动水土压力是E处主动侧向有效土压力（此时σ'=σE）和孔隙水压力（水压力是各向同性的）之和。从以上分析和判断可以看出，朗肯主动和被动土压力计算，只是计算了土的主动和被动土压力，未将地层中孔隙水的压力计算在内。

根据《建筑基坑支护技术规程》：

地下水位以上或水土合算的土层，主动土压力采用下式计算：

P=σtan2（45°-φ/2）-2ctan（45°-φ/2） （1）

对于水土分算的土层，主动水土压力为：

P=σ'tan2（45°-φ/2）-2ctan（45°-φ/2）+μ （2）

当孔隙水为静止状态时，μ=?whw。σ'=?'h。根据饱和土的物理性质指标，可以推导出?'（土在孔隙水中的浮重度）的计算公式?'=?sat-?w。

根据有效应力原理和朗肯土压力理论，式（2）可以认为是所有土体地层的主动水土压力计算公式，无论是黏性土、粉土还是砂性土，地下水位以上的土层是无孔隙水的，孔隙水压力（μ）为零，土的有效法向应力（σ'）是地层的自重应力，简算之后主动水土压力计算公式实际上是式（1）中所说的“水土合算”公式。对于争论最多的黏性土，由于黏性土中细颗粒直径小（小于0.005mm），颗粒与颗粒间的孔隙全部在毛细管现象范围内，因此只有强结合水、弱结水、毛细水或自由水，无孔隙水，适用于式（1），对于黏性土也有很低的渗透系数，应理解为是弱结水或毛细水的转换水，不能理解为孔隙水。土层全部在地下水位以下，土的孔隙中全部充满孔隙水，水渗透系数较高，孔隙水对土产生浮力，土的有效法向应力是土自重减去所受浮力后的有效重力产生的有效应力，孔隙水压力按静水压力计算。地层水土压力计算只要考虑孔隙水压力就要考虑孔隙水对土的浮力影响。

综上所述，朗肯土压力计算公式只是对土的侧向压力进行计算，未考虑土体中孔隙水压力作用，常规的计算水土压力（“水土合算”和“水土分算”）公式实际上都是符合有效应力原理的“水土分算”。

4 举例计算基坑水土压力

4.1 黏性土地层的水土压力计算

苏州市轨道交通4号线及支线工程邵昂路站⑦3粉质黏土物理性质指标如表1，黏土为可塑状态。计算此地层埋深10m处的水土压力。

根据计算公式P=σ'tan2（45°-φ/2）-2ctan（45°-φ/2）+μ

=?'htan2（45°-φ/2）-2ctan（45°-φ/2）+μ

由于粉質黏土中无孔隙水，土不受浮力作用，因此σ'=σ为黏土自重应力，?'=?为粘土自然重度18.3kN/m3，h为地层埋深10m，φ为16.5°，c为19kPa，μ为0。

计算得：

P=18.3×10×tan2（45°-16.5°/2）-2×19×tan（45°-16.5°/2）+0=73.67（kPa）

4.2 砂卵石地层的水土压力计算

成都地铁1号线一期工程文武路站〈3-7-3〉密实卵石土地层物理性质指标如表2。此地层处于地下水位线以下，计算此地层埋深10m处的水土压力。

根据计算公式P=σ'tan2（45°-φ/2）-2ctan（45°-φ/2）+μ

=?'htan2（45°-φ/2）-2ctan（45°-φ/2）+μ

其中σ'为卵石土有效应力，?'为卵石土浮重度，h为地层埋深10m，φ为42°，c为0，μ为孔隙水压力，水重度为10kN/m3。

μ=?wh=10×10=100（kPa）

?=?sat-?w=23-10=13（kN/m3）

计算得：P=13×10×tan2（45°-42°/2）-2×0×tan（45°-42°/2）+100=125.77（kPa）

5 结语

基坑支护体系中的水土压力计算完全符合太沙基的有效应力原理，并采用统一水土压力计算公式，也从侧面说明水土压力（水土分算）计算公式的正确性。由于基坑一般为露天布置，雨天地层渗水、地层水位上升等因素都会导致地层土体和孔隙水发生变化，进而导致水土压力发生变化，因此基坑支护水土压力计算按地层土体可能发生的最不利因素并预留一定的安全系数进行设计。对于不同性质土体或水位线以上和水位线以下的土体的累积水土压力计算有待于进一步研究。

参考文献

[1] 魏汝龙.总应力法计算土压力的几个问题[J].岩土工

程学报，1995，17（6）.

[2] 魏汝龙.深基坑开挖中的土压力计算[J].地基处理，

1998，9（1）.

[3] 魏汝龙.基坑内外的水压力和渗透力[J].岩土工程

师，1998，10（1）.

[4] 杨晓军，龚晓楠.基坑开挖中考虑水压力的土压力计

算[J].土木工程学报，1997，30（4）.

[5] 王洪新.水土压力分算与合算的统一算法[J].岩石力

学与工程学报，2011，30（5）.

[6] 王洪新.水土压力统一计算理论的证明及水土共同

作用下的压力计算[J].岩石力学与工程学报，2012，

31（2）.

[7] 王洪新.“对‘水土压力统一计算理论的证明及水土

共同作用下的压力计算的讨论”的回复[J].岩石力

学与工程学报，2013，32（12）.

[8] 刘发前.再论“水土合算”与“水土分算”[J].城市

道桥与防洪，2016，1（1）.

[9] 张健，胡瑞林，刘海斌，等.基于统一强度理论的朗

肯土压力的计算研究[J].岩石力学与工程学报，

2010，29（增1）.

[10] 中华人民共和国建设部.建筑基坑支护技术规程

（JGJ120-99）[S].北京：中国建筑工业出版社，1999.

[11] 徐日庆，张庆贺，刘鑫.考虑渗透性的水-土压力计

算方法[J].岩土工程学报，2012，34（5）.

[12] 汪丁健，童龙云，邱岳峰.降雨入渗条件下非饱和

土朗肯压力分析[J].岩土力学，2013，34（11）.

作者简介：王国义（1974-），男，中电建成都建设投资有限公司教授级高级工程师，研究方向：盾构技术与管理。

（责任编辑：王 波）