中国证券市场收益率的影响因素研究——基于Fama四因素的实证分析

●李 海

中国证券市场收益率的影响因素研究
——基于Fama四因素的实证分析

●李 海

本文用中国证券市场的数据来研究Fama四因素资产定价模型的应用，并检验了模型的可靠性。我们发现在Fama（1993）三因素的基础上，引入第四个动量因子在解释中国证券市场的超额收益率上有很好的帮助。研究结果表明，这四个因子在模型中都是显著的，并且常数项是不显著的。另外，高拟合优度的修正R2以及残差分析也证明我们的模型在中国证券市场上是有效的。

资本资产定价模型 四因素 证券市场收益率

一、引言

近半个世纪以来， 关于 Sharp（1964）、Lintner（1965）提出的资本资产定价（CAPM）模型可靠性的实证检验的文献层出不穷，而且早期的实证检验结果大多是支持这一模型的。资本资产定价模型认为对于风险资产的预期市场回报率应该与系统风险（市场的贝塔系数）有线性正相关的关系，然而这一理论的模型中仅仅考虑了这唯一的变量。但是，在后续的研究中，很多学者发现除了市场贝塔系数以外，还有一些与公司特性相关的变量对于平均市场回报率有很好的解释能力。比如，Banz（1981）提出了公司规模这一因素对市场回报率的解释作用，Rosenberg（1985）提出了账面市值比（B/M ratio）这个变量等等。

基于这些学者探索的启发，Fama和French（1992）（以下简称FF）在对美国股票市场的平均回报率与市场贝塔系数和若干针对公司特性的变量的关系的研究中发现，公司规模和账面市值比这两个因素对市场平均回报率有显著的解释作用。后来FF（1993）在他们的后续研究中，提出了基于传统CAPM理论的FF三因素模型。FF三因素模型的三个因素分别是市场因素（超额市场回报率）、公司规模因素 （SMB）和账面市值比因素（HML）。SMB是指由公司规模较小的上市公司的股票组成的投资组合的收益率减去由公司规模较大的上市公司的股票组成的投资组合的收益率，HML是指由账面市值比高的上市公司股票组成的投资组合的收益率减去由账面市值比较低的上市公司股票组成的投资组合的收益率。FF发现他们的三因素模型在解释市场回报率上十分有效，但是短期的动量效应并没有得到很好的解释。

Jegadeesh和Titman（1993）年提出动量效应，认为股票的收益率有延续原来的运动方向的趋势，即过去一段时间内收益率较好（较坏）的股票有着继续表现优异（差劲）的趋势。根据这一理论制定的投资策略选择买进过去三个月到十二个月收益率较高的股票而卖空收益率低的股票，这种动量策略在证券市场有着很显著的效益。于是，为了研究动量效应对市场收益率的贡献，Carhart(1997)在他的研究中提出了一个动量因子WML。WML是指由收益率较高的证券构成投资组合的收益率减去由收益率较低的证券构成投资组合的收益率。把这一因素加入FF三因素模型便形成了FF四因素模型。

很多学者在亚洲市场用上述模型做了实证分析，比如 Ho(2000)、Lam(2002)在他们的研究中表明了公司规模效应和账面市值比效应在香港市场上是显著的。Drew和 Veeraraghavan(2003)、Shum和Tang(2005)也在他们的研究中关于三因素在香港、韩国、马来西亚、菲律宾、台湾市场上得出了类似的结论。另外也有一些文献总结了动量效应，比如Fong（2005）用了24个国家的股指数据来检验动量效应的可靠性，Lam（2009）研究了四因素模型在香港市场的稳健性，但在亚洲市场上的实证分析还是相对较少。

本文尝试利用1998年5月到2014年11月的A股市场数据，来研究FF四因素资本资产定价模型在中国证券市场稳健性，并检验除了市场贝塔系数以外，其他因素在解释中国证券市场收益率的显著性。另外，本文还对A股市场的投资者提供了资产定价的解释，可以帮助投资者在实际投资行为的过程中更好地理解A股市场上证券的定价和成本的估算。

本文其余部分安排如下，第二部分主要介绍了如何构建FF四因素模型和数据的处理方法，第三部分展示了实证分析的结果，第四部分给出了本文的结论。

二、模型与数据处理

（一）样本选择

本文用到的所有数据都来自国泰安数据库，数据集包含了从1998年5月到2014年11月的A股市场635个上市公司的月度交易数据。其中，635个公司是从所有A股市场上市公司里面进行筛选得出的最终结果。被剔除的上市公司有以下原因：在样本时间段内有大量月份交易数据缺失、月度收益率有极端的变化（排除极端异常值的影响）。

无风险收益率由央行公布的一年期整存整取定期利率作为年度利率基准，按照复利计算方法折算出的月度利率。市场回报率是不考虑现金红利再投资的等均值法算出的综合月市场回报率。个股月收益率是不考虑现金红利再投资的月个股回报率。

公司市值是根据月内所有个股的总市值 （发行总股数×月收盘价）汇总数得出的，其计量货币为人民币元。账面市值比（B/M）是按照资产总计除以市值来计算的。

每一年的5月到下一年的5月为一个时间段，把所有635只股票按照市值分为两个组合，一个组合包含公司市值小的股票（S），另一个包含公司市值大的股票（B）。再分别在这两个组合里根据账面市值比从高到低分成三个组合（H、M、L）。这样就形成了六个包含大约相等数量股票的投资组合，分别是SL、SM、SH、BL、BM、BH。这六个投资组合的月度收益率是用等权重法计算投资组合里所有股票12个月内每个月的平均收益率计算出来的，重复同样的方法就可以得到

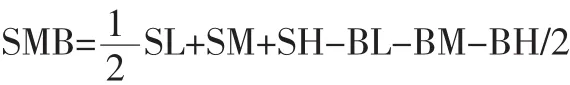
HML是指由账面市值比高的上市公司股票组成的投资组合的收益率减去由账面市值比较低的上市公司股票组成的投资组合的收益率：六个投资组合在1998年5月到2014年11月的所有月度收益率数据。

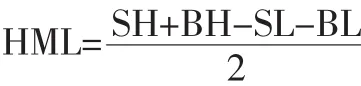
SMB是指由公司规模较小的上市公司的股票组成的投资组合的收益率减去由公司规模较大的上市公司的股票组成的投资组合的收益率：

在过去的12个月内，所有股票按照月收益率从高到低排序，收益率较高（前30%）的股票构成的投资组合为T，收益率较低（后30%）的股票构成的投资组合为B，中间40%的股票样本舍去。再分别在T、B两个组合内按公司市值从低到高排序分成两个组。这样便形成大约包含相等数量股票的四个投资组合，分别是ST、BT、SB、BB。这四个投资组合的月度收益率也是按照等权重法计算投资组合里所有股票12个月内每个月的平均收益率计算出来的。同上所述，每一年重复这种做法便可得到这四个投资组合在1998年5月到2014年11月的所有月度收益率数据。

WML是指由收益率较高的股票构成投资组合的收益率减去由收益率较低的股票构成投资组合的收益率：

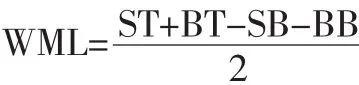
（二）FF四因素模型

在FF三因素里，三个因子分别为传统的市场因子和两个与市值和账面市值比相关的风险因子。三因素模型指出超出无风险利率的风险资产投资组合预期的收益率（即超额收益率E(Rp)-rf）可以被三个因子解释，分别是：市场溢价MP、市值溢价SMB、账面市值比溢价HML。市场溢价MP是市场投资组合的超额收益率（即Rm-rf），SMB和HML分别是之前介绍的两个构建的零融资投资组合的收益率。三因子模型的表达式为：

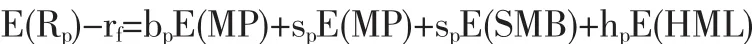
由于FF三因素没有考虑到动量效应，我们在三因素的基础上加入一个新的因子WML，即之前介绍的构建的零融资投资组合的收益率。最终，我们想要检验的四因素模型按如下表达式构建：

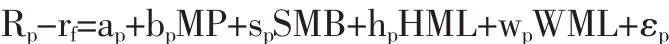
其中 Rp-rf是投资组合的超额收益率，εp是假定均值为0并且与其他变量不相关的残差项。bp、sp、hp、wp是四个因子的回归系数。

（三）实证研究

为了检验四因素模型的稳健性，我们构建了25个投资组合。根据第一年年末的公司市值从小到大，将所有635只股票分成5个组合，第一个组合包含市值最小的20%的股票，第五个组合包含市值最大的20%的股票。然后分别在这5个组合里按照该年年末的公司账面市值比从低到高分为5个组合，这样便构建了25个包含大约相等数量股票的投资组合。分别对每一组按照等权重法计算12个月内每个月所有股票平均月度收益率，然后每年重复同样的做法便得到了25个组合从1998年5月到2014年11月的所有月度收益率数据。

我们分别用这25个投资组合的月度收益率减去月度无风险利率，然后对四个因子进行回归。在预期的结果中，我们期望看到常数项ap显著等于0，否则与CAPM的超额收益率理论不符。另外我们预期四个因子的回归系数（bp、sp、hp、wp）应该显著不为零，从而说明在我们研究的A股市场上，四个因子对投资组合收益率的解释能力是显著的。

除此之外，我们还对模型的残差进行了检验，残差应该满足独立同分布的假设，这样可以进一步提升模型的有效性。

三、实证结果分析

（一）统计量概要

附录表1里展现了四个回归因子的基本统计量的综述，从四个变量的均值和标准误可以看出，四个分布都近似正太分布，没有出现奇异的分布曲线。另外四个变量的峰度系数（Kurtosis）均是负值，且绝对值与0都比较接近，都没有出现尖峰厚尾现象，所以可以排除极值对回归的干扰这一现象。

附录表2展示了25个投资组合在中国证券市场上的平均市值和账面市值比的描述性的统计量。在表2上半部分的表格里，我们发现市值与账面市值比有着正相关的关系。即在每一个市值分类的组合里面，尽管有些趋势并不明显，但是随着账面市值比的五分位数不断提高，组合的平均市值大致呈现上升的趋势。在表2下半部分的表格里，我们发现这一现象更为显著，在不同账面市值比分类的组合里面，随着市值的五分位数不断变大，组合平均账面市值比在五列里面均有强烈的升高的趋势。这一结论与其他学者在亚洲市场上的研究有所不同，但是我们认为在中国证券市场上，这一结论还是符合预期的。因为在中国证券市场上，占主导地位的还是一些大型的上市公司与国有企业。相比之下，亚洲市场比如香港、新加坡等证券市场中占主导地位的大型公司并不多。

（二）回归结果

附录表3展示了25个投资组合月度超额收益率时间序列对四个因子MP、SMB、HML、WML回归的结果。结果表明在中国证券市场上这四个因子对风险资产投资组合的超额收益率还是有解释作用的。我们可以看到25个常数（ap）系数里，绝大多数都不显著不等于0，这说明我们构建的模型是有效的，符合CAPM的超额收益理论。25个贝塔系数（bp）全部高度显著（在1%置信水平下）接近于1，其t统计量从26.72到55.58不等进一步说明显著性很高。虽然我们并没有发现贝塔系数在每个账面市值比分位数下随着市值的变化有明显的变化趋势，但是在研究过程中，我们发现公司的收益率与市值大致呈现负相关关系。即市值较小的公司往往有较高的收益，市值较大的公司反而收益率不那么可观。但总而言之，在我们的研究中我们发现市场溢价（MP）这一因子在中国证券市场上对超额收益率的贡献显著毫无疑问是令人信服的，其很好地解释了资产回报与系统风险的关系，这也与传统的CAPM理论是契合的。

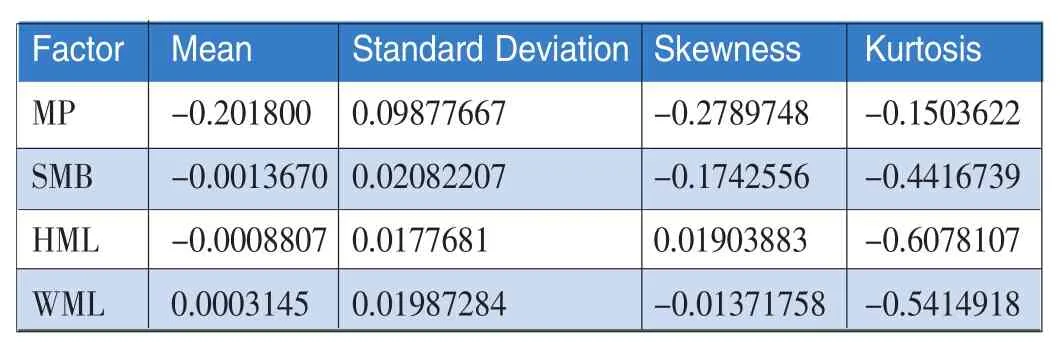
表1

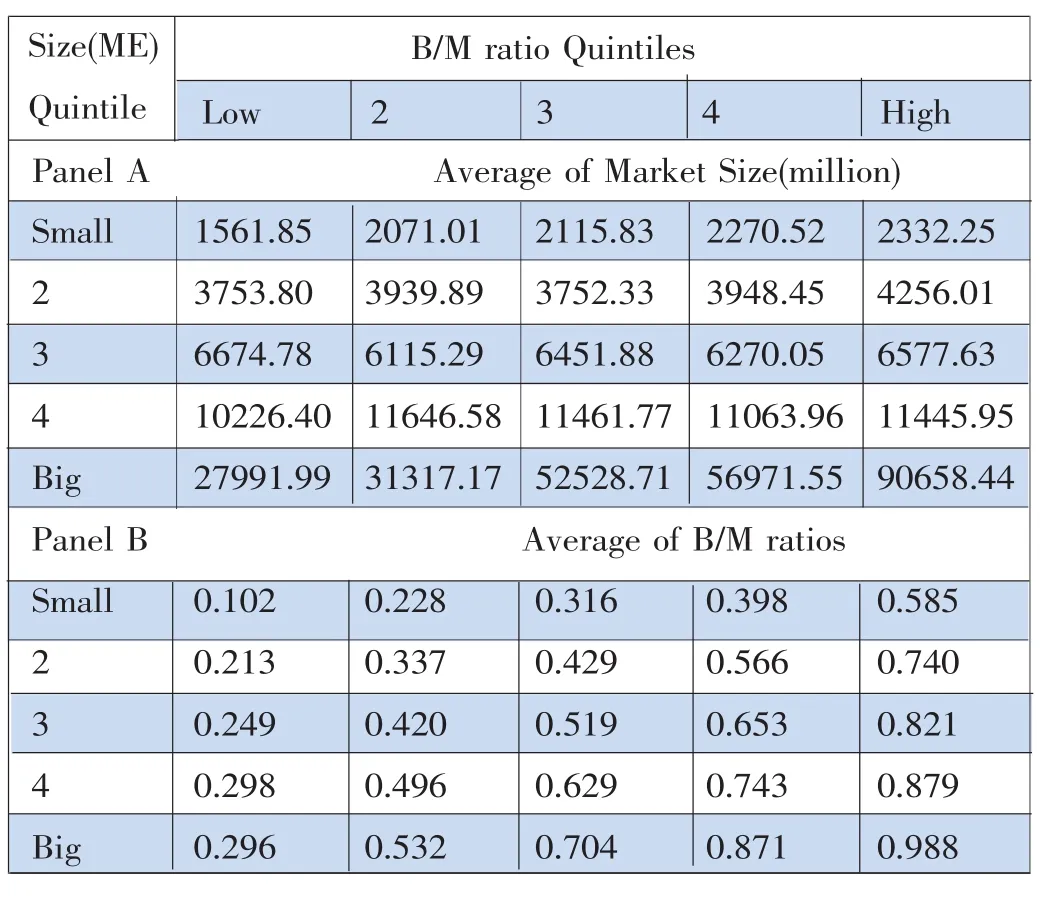
表2

市值因子（SMB）的回归系数 sp从-1.04变化到1.07，而且除了三个系数以外，都在1%置信水平下显著。我们发现市值因子与市值有强烈的负相关关系，在每个账面市值比五分位数下，随着组合平均市值的升高，回归系数 sp从正值单调下降到负值。这一结果也是符合预期的，市值因子会随着市值变化而变化，这与FF（1993）的研究结果是类似的。

账面市值比因子（HML）的回归系数 hp相对 sp来说显著性不那么高，只有接近一半的值至少在5%置信水平下显著。与市值因子与市值的关系有相同的道理，我们发现控制住组合平均市值不变，随着账面市值比五分位数不断提高，回归系数hp大致呈上升趋势，这一结果也是符合预期的。另外我们发现，随着市值和账面市值比的升高，回归系数 hp从负值慢慢变成正值，在高市值高账面市值比的组合里系数高度显著 （1%置信水平下）接近于1。在我们对中国证券市场的研究中，与市值因子（SML）一样，账面市值比因子（HML）对风险资产超额回报率也起到了很好的解释作用，这两个因子弥补了市场溢价因子（MP）解释不了的关于市场上微观的公司风险的部分。

动量因子（WML）的回归系数 wp从-0.89变动到0.59，超过一半以上的系数为负值，虽然没有观察到与市值和账面市值比有明显相关性，但是 wp在市值小和账面市值比低的投资组合里为正值的概率大，在市值大和账面市值比高的投资组合里为负值的概率大。另外在回归结果中，wp显著性也是可以的，八个系数在1%置信水平下显著，两个系数在5%置信水平下显著，还有两个系数在10%置信水平下显著。

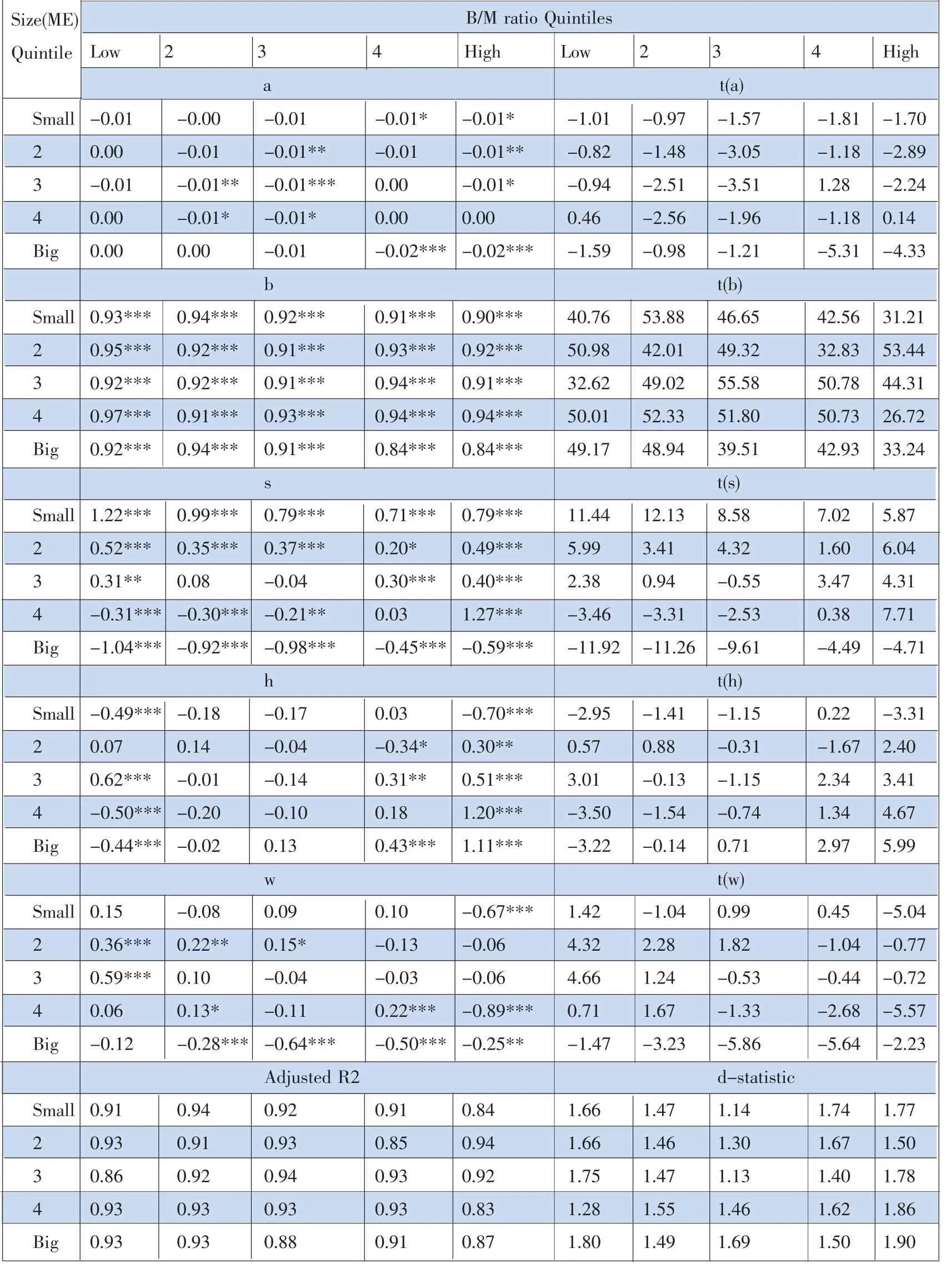
表3

表3里还展示了25个投资组合超额收益率对四因子回归的修 正 R2和 Durbin-Watson统计量。25个修正 R2从0.83到0.94不等，平均值达到了0.91，说明回归的拟合度是十分优良的。而且在市值高的投资组合里，修正 R2相较于市值低的投资组合里平均要高一点，说明在市值高的投资组合里，四因子能更好地解释超额收益率。DW统计量从1.14到1.90不等，从中没有发现明显的自相关问题。

为了进一步检验模型的有效性，我们对回归得到的残差进行了LM序列自相关检验。从表四我们可以看出，在5%的置信水平下，25个回归方程里只有六个回归方程的残差的p值小于0.05，从而拒绝序列不存在自相关的原假设，说明模型的残差总体上是服从独立分布的，这也进一步说明四因素模型是有效的。而且我们发现，在高市值和高账面市值比的投资组合里，残差的自相关性都不显著，说明模型在这种组合里的效率更好。

总的来说，在我们对中国证券市场的研究中，四个因素共同构建的模型对风险资产投资承担风险所要求的超额收益率的解释的可靠性还是令人满意的。

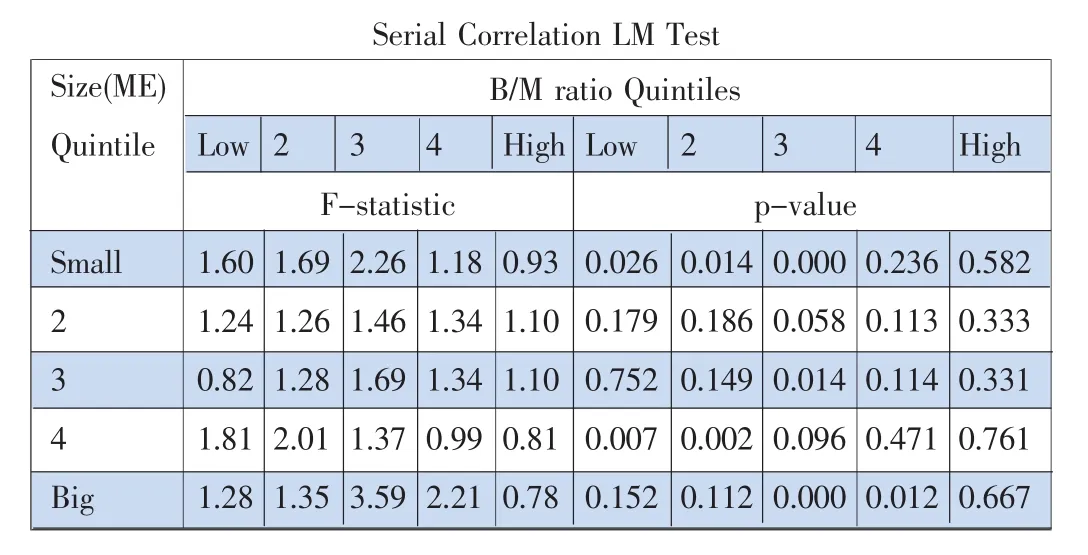
表4

四、结论

本文用1998年5月到2014年11月的中国A股市场交易数据验证了四因素资产定价模型在中国市场的应用的可靠性，四因素资产定价模型包含了市场溢价因子（MP）、市值因子（SMB）、账面市值比因子（HML）、动量因子（WML）。并检验除了市场贝塔系数以外，其他因素在解释中国证券市场超额收益率的显著性。

我们的研究结果表明，这四个因素能很好地解释我们在中国证券市场上构造的风险资产投资组合的超额收益率的变动。四个因子的回归系数的显著性和常数项的不显著不等于0都提供了有说服力的证据。除此之外，高拟合优度的修正R2也证明我们的模型在中国证券市场上是有效的。

另外，本文还对A股市场的投资者提供了实际资产定价的解释。在个人投资者或者机构投资者选择投资组合的过程中，本文构建的可靠的定价模型可以帮助他们更好的理解A股市场上证券或资产的定价和成本的估算。

（作者单位：武汉大学经济与管理学院）

[1]代晶，杨磊，敖仪斌.基于内部收益率指标的合同能源管理项目融资方案探讨[J].建筑经济，2015，（03）.

[2]范建华,张静.基于Fama-French三因子模型的沪深300指数效应实证研究[J].重庆工商大学学报(社会科学版),2013,（30).

[3]李延军,王丽颖.股市流动性与资产定价——基于我国A股市场的实证研究[J].金融发展研究,2015，(07).

[4]王珺,杨晓红,杨凤霞.三因子模型在中国A股市场的有效性探讨 [J].湖北经济学院学报 (人文社会科学版),2013，(09).

[5]杨炘,滕召学.中国A股市场股票投资组合特征分析与Fama—French三因子模型 [J].杭州师范大学学报 (社会科学版),2003，(02).

[6]赵胜民,闫红蕾,张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据[J].南开经济研究,2016,(02).

[7]Banz R W.The relationship between return and market value of common stocks[J].Journal of Financial Economics,1981,9(1). [8]Michael Drew.Beta,Firm Size,Book-to-Market Equity and Stock Returns[J].Journal of the Asia Pacific Economy,2003,（0 8).

[9]Fama E F,French K R.The Cross‐Section of Expected Stock Returns[J].The Journal of Finance,1992,（47).

[10]Fong W M,Wong W K,Lean H H.International momentum strategies:a stochastic dominance approach[J].Journal of Financial Markets,2005,（08).

[11]YiuWah Ho,Roger Strange,Jenifer Piesse.CAPM anomalies and the pricing of equity:evidence from the Hong Kong market[J].Applied Economics,2000,（32).

[12]Jegadeesh N,Titman S.Returns to Buying Winners and Selling Losers:Implications for Stock Market Efficiency[J].The Journal of Finance,1993,（48).

[13]Lam K S K.The relationship between size,book-to-market equity ratio,earnings–price ratio,and return for the Hong Kong stock market[J].Global Finance Journal,2002,（13).

[14]Lintner J.Security prices,risk,and maximal gains from diversification[J].The Journal of Finance,1965,（20).

（本栏目责任编辑：郑洁）