基于GARCH模型的美国主权CDS息差收益率波动性研究
朱鸿涛

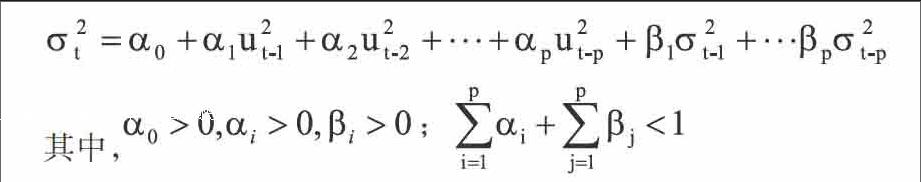
【摘要】本文以美国5年期主权CDS息差2012年9月30日至2016年9月29日的全部日度数据为研究对象。从研究美国5年期主权CDS息差收益率的基本统计特征出发,利用时间序列分析法,构建能够衡量其波动性特征的GARCH(1,1)模型,重点探究美国5年期主权CDS息差收益率的波动特征。实证分析表明,美国5年期主权CDS息差收益率具有异方差性且具有“尖峰厚尾”现象,收益率具有右侧较长尾部。GARCH(1,1)能够很好地拟合序列,适合对主权CDS息差收益率波动性作进一步研究。
【关键词】CDS ARCH效应 GARCH模型 收益率波动
一、引言
随着2009年10月希腊政府宣布其公共债务、政府财政赤字将远超《欧洲稳定与增长公约》规定的上限以及2012年3月9日,国际互换与衍生品协会认定,希腊国债出现的偿付危机将触发重组信用事件。由希腊债务危机以希腊债务危机为导火索所产生的欧洲债务危机使人们关注到,主权债务违约的可能性不仅出现在发展中国家,也出现在发达国家。
CDS信用违约互换合约由两部分组成,分别是初始名义本金以及之后定期交付的票息即息差。09年之前,多数的CDS没有名义本金而只有息差。CDS的息差反映了投资者为标的资产所愿意支付的违约风险补偿,信用保障购买方按期支付固定费用给信用保障出售方,如保障其内,标的资产发生信用违约事件,信用保障出售方支付购买方违约损失。息差支付与违约赔付关系图如图1所示:
相比于发达国家的金融市场,我国衍生品市场起步较晚,金融衍生工具品类不多,这在一定程度上制约了我国金融市场信息传导、反馈作用的发挥,不利于我国不断深化金融市场的发展要求。为此,2010年7月中国银行间市场交易商协会发布了《中国信用衍生产品创新与发展问题研究》,随后落实了细则和实施机制。2016年9月23日,协会发布《信用违约互换业务指引》及相关的配套文件。我国首批CDS交易已于2016年10月31日达成,共开展15笔CDS交易。总计名义本金3亿元,。发行人为中国银行、农业银行、工商银行、建设银行、交通银行等10家金融机构,交易期限为一年至两年不等。
虽然目前我国并未出现主权CDS及其交易市场,但国际市场上已出现的主权CDS工具值得我们关注。CDS是重要的信用缓释工具,也是目前国际上普遍采用的场外信用缓释方式。随着全球经济的一体化及我国资本账户的不断开放尤其是人民币加入SDR新货币篮子,我国金融深化的脚步进一步加快。研究以美国为例的主权CDS息差收益率波动特征,可为我国未来衍生品市场尤其是主权CDS信用违约互换产品的设计定价、政策监管方面提供一定的依据和参考。
二、文献综述
主权CDS的市场规模相对较小,目前已有的研究主要针对于发展中国家进行研究。Longstaffet al.(2007)用2000到2007年的月度数据,研究了23个新兴国家主权市场和3个发达国家主权市场。研究发现决定主权CDS溢价的因素主要是全球金融市场景气指标(美国高收益公司债券信用利差)、全球风险溢价(VIX波动率指数)和全球投资流量(共同基金债券和股票),而非各国家的特征指标,如当地股市收益率,利率,外汇储备等。
王琼、陈金贤(2003)对信用违约互换进行了包括其结构、规避信用风险机理及市场效用的定性分析,并给出了估值方法。任兆璋、李鹏(2006)构建了考虑流动性风险影响的可违约债券定价模型,分离了信用利差中所包含的违约风险与流动性风险,并在此基础上得到了流动性风险调整的信用违约互换定价。同时利用企业债券市场数据进行实证,发现,忽略流动性风险会导致对高信用级别的公司债券,尤其是到期期限较短高信用级别公司债券违约率的高估,进而造成了信用违约互换初始定价的高估。
三、实证分析
博勒斯莱文(Bollerslev)于1986年首先运用GARCH模型(广义自回归条件异方差模型,generalised ARCH model)。GARCH模型在条件方差的方程中加上了滞后项,从而可以体现更为灵活的滞后结构。GARCH(p,q)的方差方程定义为:
σ2t是由最近的p个u2观察值以及q个最新的有关方差的估计计算而得。
则GARCH(1,1)模型为:
GARCH(1,1)是到目前为止GARCH模型中最流行的一种。GARCH(1,1)表达式为 ,式中α对应ARCH项u2t-1的权重,β对应GARCH项σ2t-1的权重。
本文选取2012年9月30日至2016年9月29日美國5年期主权CDS息差日度数据作为研究对象,排除节假日等非交易日,共得到1028个数据。为了得到平稳的收益率时间序列数据,采用对报价取对数然后差分进行分析。
由描述性直方图可知,美国5年期主权CDS收益率序列均值(Mean)为-0.000412,标准差(Std.Dev.)为0.072895,偏度(Skewness)为0.637691,偏度大于0,表明该收益率具有右侧较长尾部。峰度(Kurtosis)为5.801831,高于于正态分布的峰度值3,表明CDS收益率序列具有尖峰和厚尾的特征。Jarque-Bera统计量P值为0.00000,拒绝了收益率序列服从正态分布的假设。
(一)单位根检验与ARCH效应检验
在进行实证检验之前,必须进行数据的平稳性检验,而一般我们常用的方法是采用ADF(Augment Dickey-fuller)单位根检验。检验结果如表1:
经过ADF单位根检验,t统计量的值为-33.70373,对应P值接近0,收益率序列是平稳的。又根据序列自相关和偏自相关检验,序列的自相关和偏自相关系数均落入两倍的估计标准差内,且Q-统计量的对应的p值均大于置信度0.05,故序列在5%的显著性水平上不存在显著的相关性。由于收益率序列不存在显著的相关性,因此,将均值方程设定为白噪声并设立模型。
将CDS收益率序列去均值化得到新CDS收益率序列S,并建立平方方程检验结果显示序列存在自相关,因此,存在ARCH效应。自相关函数分析图如图2所示:
(二)GARCH模型分析
利用GARCH(1,1)模型进行估计
GARCH(1,1)方程为:
方差方程中ARCH项与GARCH项的系数都是统计显著的,方差方程中ARCH项与GARCH项系数之和为0.186+0.524=0.710小于1,满足参数的约束条件,具有可预测性,GARCH(1,1)能够很好地拟合数据。同时可知其长期方差权重γ=1-α-β,ω=γVL得到长期方差VL=0.0049即模型隐含出收益率每天长期方差平均为0.0049,对应的波动率为7.00%
四、结论
一是美国5年期主权CDS息差对数收益率时间序列的均值方程是一个白噪声且具有ARCH效应。
二是异方差的存在性。美国5年期主权CDS息差收益率有“尖峰厚尾”现象,收益率具有右侧较长尾部,不服从正态分布。GARCH(1,1)能够很好地拟合序列并得到7.00%的收益率每天长期波动率,适合对主权CDS息差收益率波动性作进一步研究。
参考文献
[1]张波.次贷危机下的CDS市场:风险与变革[J].中國货币市场,2008,10:17-21.
[2]陈熹祥.CDS及其风险研究——结合金融危机分析[J].经济研究导刊,2010,03:52-53.
[3]董楠,吴文锋.海外市场的中国信用违约互换息差定价实证研究[J].科学技术与工程,2011,06:1285-1289+1306.
[4]王琼,陈金贤.信用违约互换的避险机理及价值分析[J].西安交通大学学报(社会科学版),2003,02:18-21.
[5]任兆璋,李鹏.流动性风险调整的信用违约互换定价[J].华南理工大学学报(自然科学版),2006,11:117-122.
[6]Hilscher J.Determinants of Sovereign Risk: Macroeconomic Fundamentals and the Pricing of Sovereign Debt[J].2007,14(2):235-262.

