基于Copula函数的洪峰流量与洪水历时联合分布研究

范嘉炜，黄锦林

(1.天津大学建筑工程学院，天津 300072；2. 广东省水利水电科学研究院，广州 510635)

0 引 言

洪水是一种常见的自然现象，洪水频率分析是防御洪水的关键技术内容。我国水文工作者在借鉴国外有关经验的同时，结合国内水文资料和实际情况进行了大量的水文频率分析工作。在实践中，洪峰流量作为一个重要的特征量，常用来表征水文事件的整体过程，通过点绘频率曲线、确定线形、估计参数等推求设计值，进而估算设计洪水。洪水历时作为另一个洪水特征量，同样在一定程度上反映了洪水的演进过程，并与洪峰流量具有较强的相关性，洪水历时较短时，洪峰传递过程削减较快，洪峰衰减，反之，洪水历时较长时，洪峰流量传递过程延长，峰值增大。要想全面地了解其具有的统计规律，就必须通过多个方面的特征属性来对它进行定义和描述。但是，在实践中人们往往只进行单个变量的频率分析，即用一个特征量来代表洪水事件的整体特征: 我国水文界通过大量分析研究，得出P-Ⅲ分布函数对洪峰流量拟合效果较好[1]，作为我国较为普遍的线形；对于洪水历时的边际分布拟合的主要应用有Gamma分布、Gumbel分布[2]、指数分布[3]以及对数正态分布[4]等。随着研究问题的复杂性，单变量分析将难以达到设计的要求[5]。

近年来，用Copula函数[6,7]进行洪水过程分析成为水文计算领域的一个研究热点，这种分析方法能更好地描述洪水随机变量间的内在规律和关系。目前Copula在水文频率分析中主要应用于以下方面：暴雨、洪水、干旱等极值水文事件的多变量联合分布研究[8,9]，分析防洪系统中设计洪水地区组成[10]，神经网络径流预报的预报因子选择方法优化[11]，不同季节旱涝组合概率特征分析[12]，考虑气候变化的区域性干旱预测[13]等问题，而对于洪峰流量和洪水历时的联合频率分布的研究以及变量间的组合风险分析相对较少。本文以潖江流域的大庙峡为例，选取洪峰流量与洪水历时2变量，通过数据分析后选择P-Ⅲ分布和对数正态分布分别构建洪峰和历时的边缘分布函数，利用G-H Copula建立2者的联合与同现概率分布，并探讨了2变量在不同重现期情况下的组合概率分布情况，以期为防洪减灾和水利工程规划提供参考依据。

1 研究方法

1.1 边缘分布函数

(1)P-Ⅲ型分布函数。对于水文变量的频率曲线选择问题，我国学者们通过大量研究发现P -Ⅲ分布函数对于洪水要素的拟合效果较好，目前应用也较为普遍。P -Ⅲ分布参数可选用概率权重法进行估计，其中H、R是与Cs有关的参数，通过对样本的前3阶距M0,M1,M2的估计，便可得出P -Ⅲ曲线的参数：

(2)

(2)对数正态分布函数。对数正态分布是一种连续型分布。它可用于描述某些呈偏态分布的资料。如果随机变量经对数变换后服从正态分布，就说明此变量服从对数正态分布。对数正态分布拟合洪水历时等变量具有较好的效果：

(3)

式中：μ、σ分别为变量对数值lnx系列的均值和标准差。

对数正态分布参数可选用极大似然估计法进行估计，首先建立极大似然函数，根据定义，解极大似然方程得到的参数值则为极大似然估计值，由于篇幅所限，此处只给出推导结果如下：

lL(μ,σ|x1,x2,…,xn)=

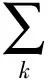
(4)

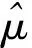
1.2 Copula函数与参数估计

Copula是定义域为[0,1]均匀分布的多维联合分布函数，它可以将多个随机变量的边缘分布连接起来得到它们的联合分布，早在1959年即被提出，但直到20世纪90年代该方法才得以迅速发展，成为统计学中的一个新的课题。

Sklar[14]定理:令H为一个n维分布函数，其边缘分布为F1,F2,…,Fn，则存在一个n-Copula函数C，使得对任意x∈R有：

H(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(5)

Copula函数的优点在于不必要求具有相同的边缘分布，任意边缘分布经过Copula函数连接都可构造成联合分布，由于变量的所有信息都包含在边缘分布里，在转换过程中不会产生信息失真。

Copula函数总体上可以划分为3类:椭圆型、二次型和Archimedean型，以第3类Archimedean型函数应用最为广泛。多维Archimedean Copula函数的构造通常是基于二维的，其结构简单，可以构造出多种形式多样、适应性强的多变量联合分布函数，具有广泛的应用价值。常见的二维Archimedean Copula函数包括： Clayton Copula、Gumbel-Hougaard(G-H)Copula 、Ali-Mikhail-Haq (AMH)Copula、Frank Copula，Nelson[15]对Archimedean Copula函数及其性质进行了详细的介绍，见表1。

表1 函数类型与参数Tab.1 Function type and parameter

本文采用相关性指标法[16]对Copula函数中的参数θ进行估计。建立kendall秩相关系数τ与θ的关系， 其中kendall秩相关系数[17]表示为：

(6)

式中:τ为kendall秩相关系数；(xi,yi)为测点据；sgn(·)为符号函数；n为系列长度。

估计各种Copula函数的参数θ后，可以建立洪峰和历时的Gumbel-Hougaard(G-H) Copula函数、Clayton Copula函数、Ali-Mikhail-Haq (AMH)Copula函数和Frank Copula函数的联合频率分布。

1.3 拟合优度评价

要知道哪一种Copula函数反映洪水事件的真实特性，能更准确地描述变量间的相关结构，就需要对Copula函数进行拟合优度评价，以选择最合适的Copula函数来描述变量之间的相关结构，最终确定最优的Copula函数。常用的拟合优度评价的方法有离差平方和准则法(OLS)[18]、AIC信息准则法[19,20]等。本文采用AIC和OLS进行Copula函数的拟合优度评价以确定最优的Copula函数。

(1)AIC准则。即：

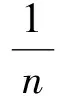
(7)

AIC=nln (MSE)+2k

(2)OLS准则。即：

(8)

式中：Femp(xi1,xi2,…,xim)为经验频率值；C(ui1,ui2,…,uim为理论频率值；k为参数个数；m为维数。

Copula函数拟合越好，则AIC值与OLS值越小。

2 实例分析

2.1 背景资料

大庙峡位于广东佛冈县石角镇南面的北江河段，属山区性河流，全长约6 km，两岸高山对峙，山势险要，上游段河道比降0.38%～0.98%，洪水汇流快，洪峰尖瘦，10 a一遇洪水洪峰模数6～10 m3/(s·km2)，下游为丘陵平原区，主河道洪峰模数较少，约3～5 m3/(s·km2)。由于境内河流都属山区型，集雨区山地陡峭，河床比降大。该区域全年降雨天数多达166 d，次数多，来势猛，是广东多暴雨的地区之一。汛期暴雨后，河道渲泄不畅，易造成洪涝灾害。该地区山洪特点是暴涨暴落、历时短，一般山洪以单峰为主，单峰型山洪历时一般为1～3 d。山洪特性可归纳为“四大、两快、一短”，即山洪流速大、冲刷力大、含沙量大及破坏力大；“两快一短”是指山洪涨得快、落的快、历时短。1960年1月1日设立省级水文站——大庙峡水文站。大庙峡水文站设立以来，在其辖下的10多个雨量站的协调配合下，至今已积累了50 a以上的降雨、水位、流量等水文测验资料，代表性和稳定性较好。

本文采用潖江流域大庙峡水文站1960-2014年的洪水资料为例，选取该水文站的年最大洪水所对应的洪峰流量和洪水历时作为所研究的特征变量，运用Copula函数中的G-H Copula对潖江河流域大庙峡水文站址处洪水的洪峰和历时进行联合分布研究，推求2变量联合分布函数及联合重现期，并与单变量洪水频率计算进行比较分析，分析结果对潖江河流域的防洪减灾、调度管理、洪水资源合理规划等有重要的意义。

2.2 边缘分布函数确定

运用概率权重法公式(2)估计洪峰服从的P-Ⅲ分布函数的参数值，运用极大似然法公式(4)估计历时服从的对数正态分布函数的参数值，可得洪峰和历时的统计参数，可得大庙峡水文站洪峰流量P-Ⅲ频率曲线。采用Q均值=785 m3/s，Cv=0.65，Cs=1.22，倍比Cs/Cv=3.5。频率曲线适线考虑了整体系列经验频率，不单以配合高水点据为原则。洪水历时服从对数正态分布，即给定的变量取对数后服从正态分布。

采用文献[21]中的极大似然法估计对数正态分布函数的参数，得到洪水历时分布的参数为μ=3.2,σ=0.29。图1、图2为拟合的2变量频率累积曲线。

图1 洪峰流量频率累积曲线Fig.1 The peak flow frequency curve

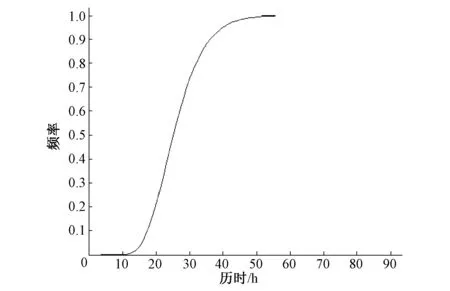
图2 洪水历时频率累积曲线Fig.2 Flood duration frequency curve

2.3 最优Copula函数选择

在本例中选择Copula函数中常见的4种二维Archimedean Copula函数进行参数估计，并从中选择最优函数拟合变量。首先，运用公式(6)计算洪峰与历时的Kendall秩相关系数得到τ=0.713 6，运用相关性指标法计算公式计算洪峰和历时2变量联合频率分布模型的参数，得到4种二维Archimedean Copula函数的参数θ，见表2。

表2 Archimedean Copula参数θTab.2 Archimedean Copula parameter θ

采用AIC信息准则法和OLS离差平方和准则法进行Copula函数的拟合优度评价以确定最优的Copula函数，计算结果见表3。

表3 AIC与OLS拟合优度评价Tab.3 Evaluation of AIC and OLS

根据表3数据显示，Gumbel-Hougaard(G-H)Copula对于洪峰历时的联合分布拟合效果最好，因此，将计算得到的参数代入，建立潖江河大庙峡流域洪峰和历时2变量G-H Copula函数的联合频率分布函数。

2.4 洪峰历时联合分析

运用前文分析计算得出的最优Copula函数——G-H Copula，建立洪峰和历时两特征变量的联合分布、同现分布以及2变量的组合频率分布[22,23]。同现频率用公式(9)表示，组合频率分布用公式(10)表示，联合重现期和同现重现期分别用公式(11)、(12)表示：

H′(x1,y1)=P(X1>x1,Y1>y1)=

1-u1-u2+C(u1,u2)

(9)

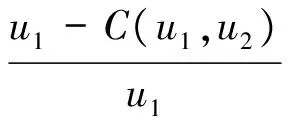
(10)

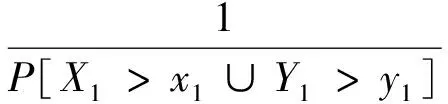
(11)

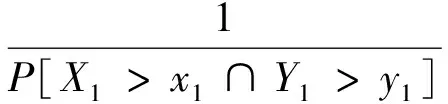
(12)

式中，X1和Y1为假定的具有相关关系的特征变量序列；u1,u2分别为边缘分布函数；C(u1,u2)为联合频率分布函数。

由G-H Copula函数拟合后得到2变量的联合频率分布，根据公式(9)可以得到2变量同现频率分布，见图3、图4。根据其等值线图(图5、图6)可分别查到给定2变量条件下洪水变量发生的频率。以2变量联合频率分布为例，洪峰小于705 m3/s情况下，历时在30 h以下的频率为0.5；洪峰小于1 095 m3/s情况下，历时在30 h以下的频率为0.7。同理，以2变量同现频率分布为例，洪峰大于1 155 m3/s且洪水历时在25 h以上的频率为0.2；洪峰大于465 m3/s且洪水历时在25 h以上的频率为0.5。

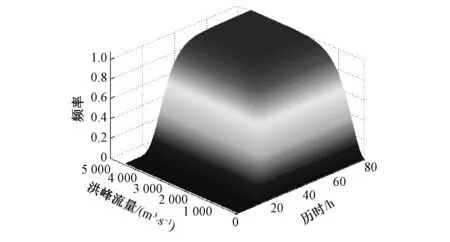
图3 洪峰、历时联合频率分布图Fig.3 Distribution of joint frequency

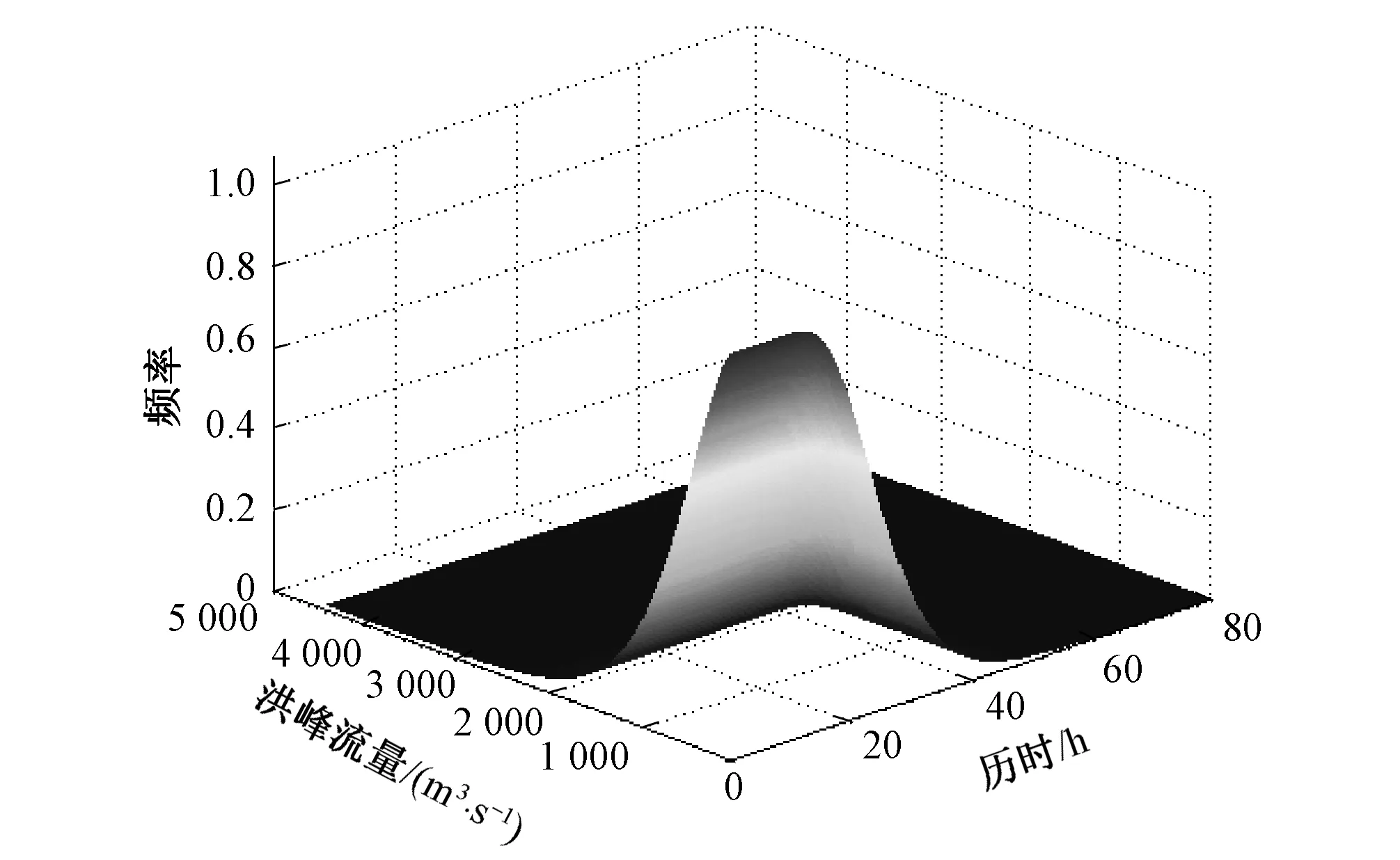
图4 洪峰、历时同现频率分布图 Fig.4 Distribution of simultaneous frequency

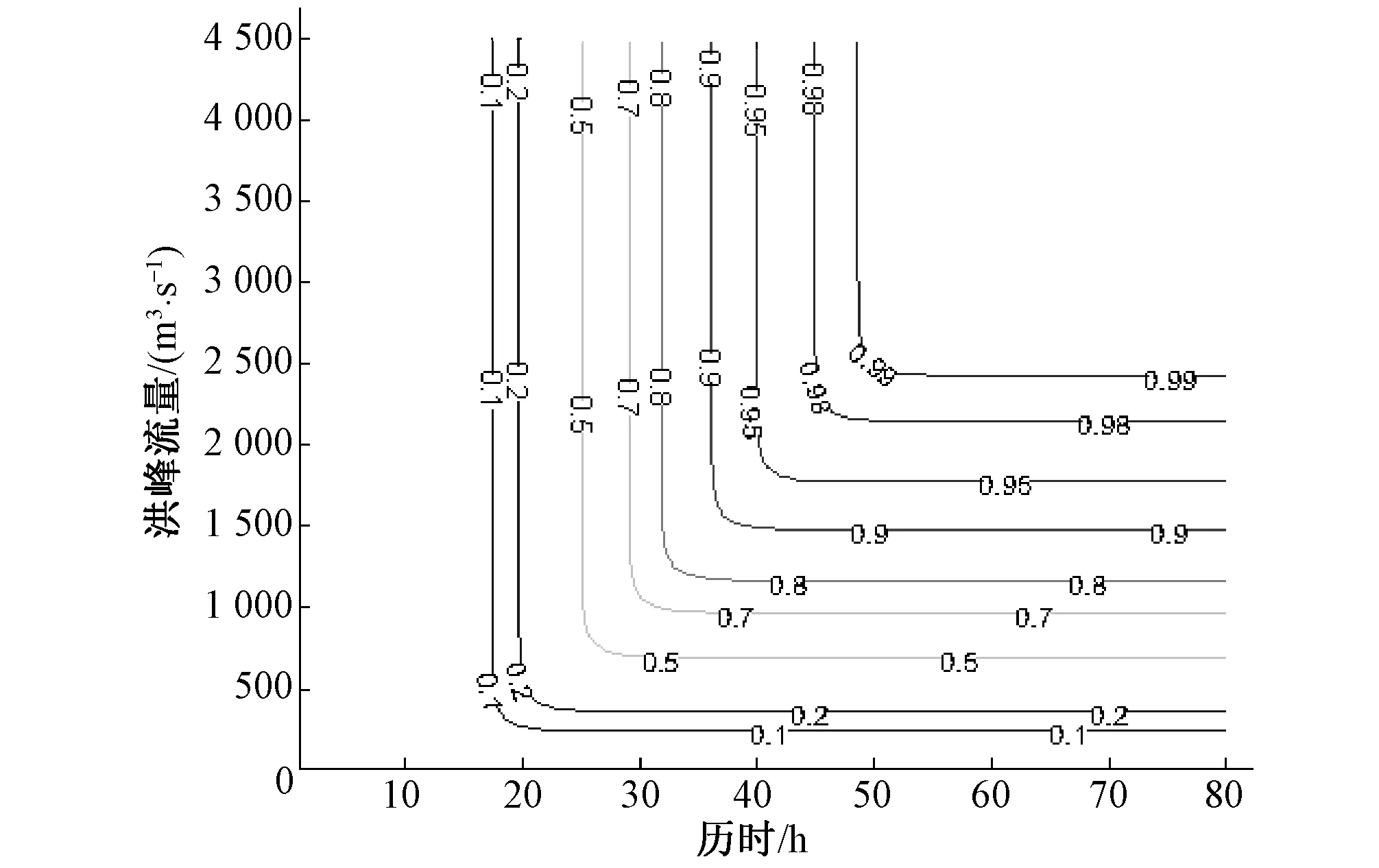
图5 洪峰、历时联合频率分布等值线图Fig.5 Contour of joint frequency

图6 洪峰、历时同现频率分布等值线图Fig.6 Contour of simultaneous frequency

根据公式(11)、(12)可以得到2变量联合重现期和同现重现期分布，见图7、图8。同时可以得到2变量在不同重现期下的各种组合，与单变量的结果相比能更全面地反映洪水要素之间的相关关系。基于前面得到的洪峰流量与洪水历时的边缘分布，计算得到不同设计重现期下的单变量设计值。利用联合重现期等值线图(图9)和同现重现期等值线图(图10)可以分别得出在此设计值下的重现期。计算结果见表4。例如，给定边缘分布设计重现期为200 a，由边缘分布函数求得单变量情况下的洪峰设计值为2 850 m3/s，历时设计值为52.3 h。由图9查得此单变量设计值下的联合重现期为187.5 a，由图10查得同现重现期为308.9 a。又如设计重现期为50 a，求得单变量情况下的洪峰设计值为2 150 m3/s，历时设计值为45.0 h。此单变量设计值下联合重现期为40.9 a，同现重现期为63.7 a。由此可以看出，2变量联合重现期均低于单变量设计重现期，而同现重现期均高于单变量设计重现期。在实际的工程应用中，联合重现期和同现重现期分别适用于2种遭遇情况，若洪峰

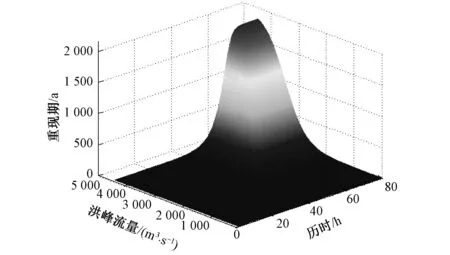
图7 洪峰、历时联合重现期分布图Fig.7 Distribution of joint return period

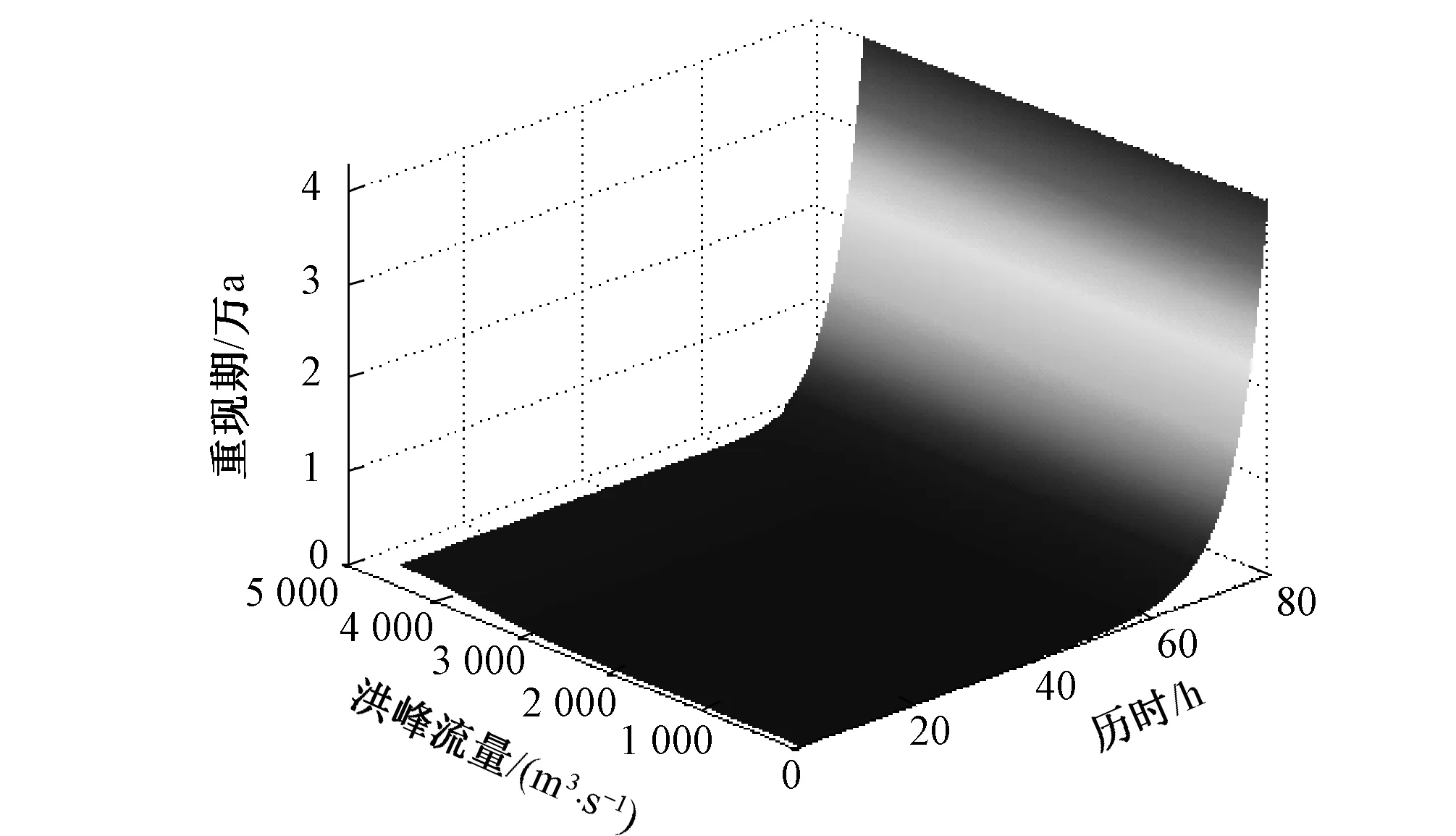
图8 洪峰、历时同现重现期分布图Fig.8 Distribution of simultaneous return period

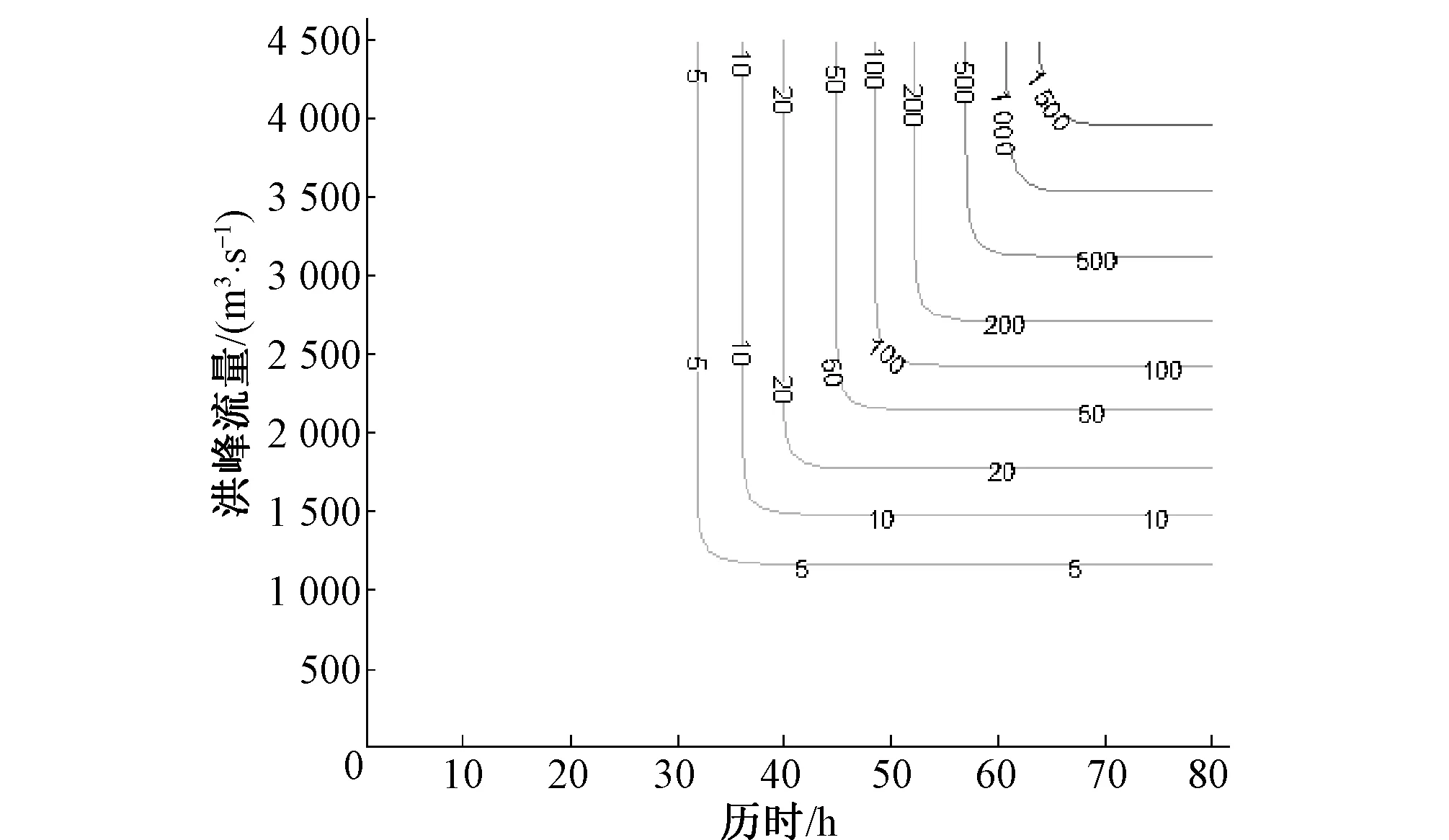
图9 洪峰、历时联合重现期等值线图Fig.9 Contour of joint return period

和历时的设计值2者中有一个被超过，则被认为是破坏，此时应该用联合重现期来描述实际重现期；若洪峰和历时的设计值都被超过时才被认为是破坏，则应采用同现重现期来描述实际重现期。

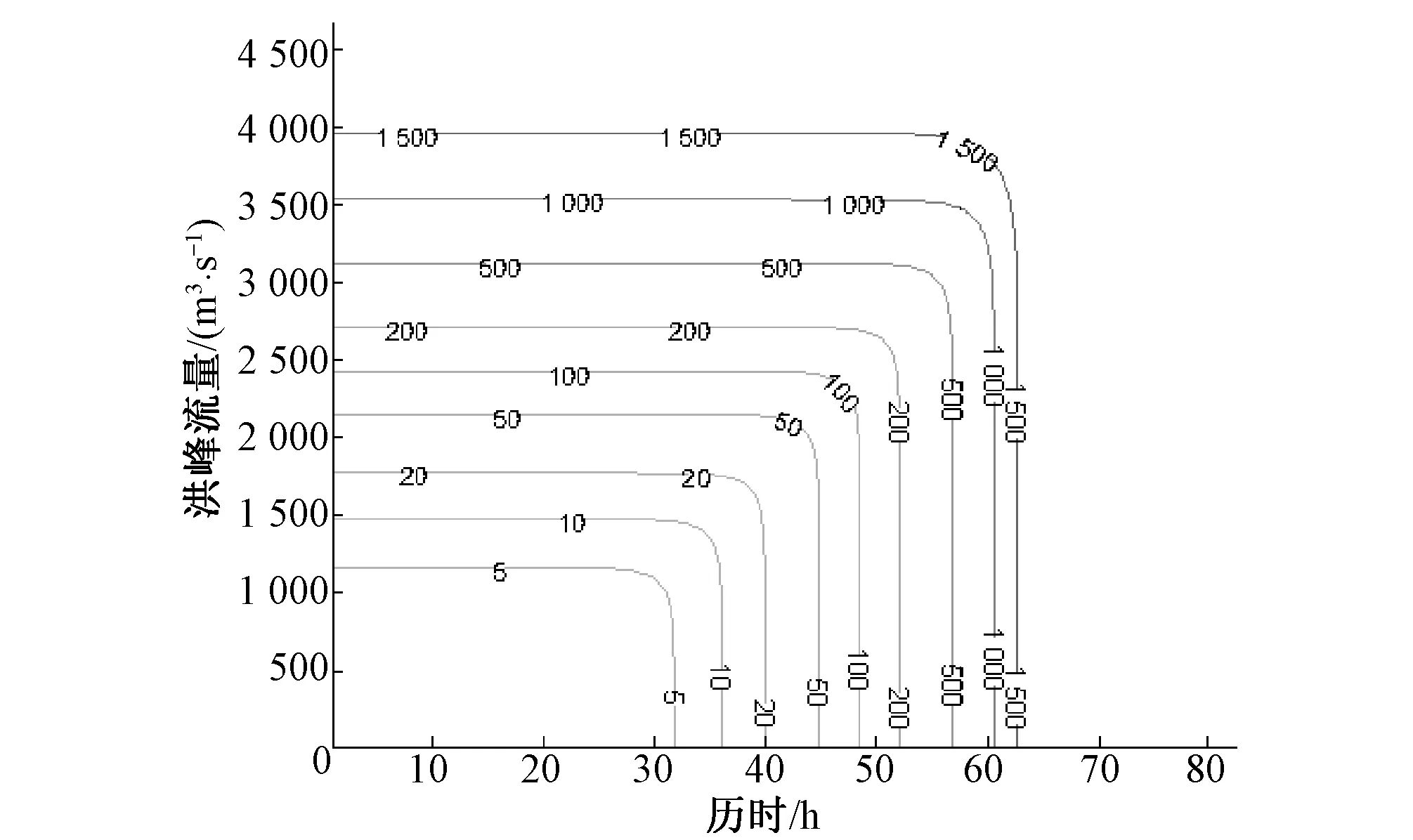
图10 洪峰、历时同现重现期等值线图Fig.10 Contour of simultaneous return period

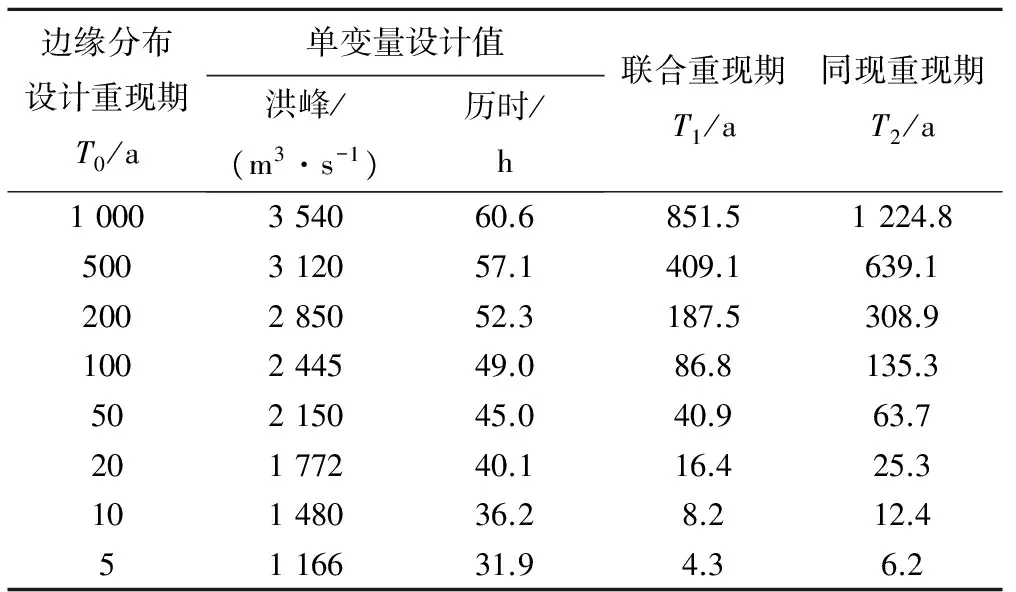
边缘分布设计重现期T0/a单变量设计值洪峰/(m3·s-1)历时/h联合重现期T1/a同现重现期T2/a1000354060．6851．51224．8500312057．1409．1639．1200285052．3187．5308．9100244549．086．8135．350215045．040．963．720177240．116．425．310148036．28．212．45116631．94．36．2

采用洪峰流量与洪水历时同频率的假定，在给定一定重现期下，基于G-H Copula函数反求得2变量的同频率值，再通过边缘分布函数分别得到相应的设计洪峰和设计历时值，结果见表5。对比表4和表5可以得出，基于2变量联合分布的设计值均高于单变量情况下计算得到的设计值。以1 000 a设计重现期为例，单变量情况下洪峰设计值为3 540 m3/s，历时设计值为60.6 h；2变量联合分布情况下洪峰设计值为3 675 m3/s，历时设计值为62 h。可以看出，基于单变量推算的设计值实际上达不到所要求的标准，基于2变量联合分布的设计结果与单变量设计结果相比更为安全、可靠。

表5 2变量联合分布设计值Tab.5 Design value of joint distribution

根据式(10)定义，建立洪水历时与洪峰流量的组合频率分布(见图11、图12)，即当历时小于某一设定值T1时，对应洪峰流量可能超过设定值Q1的概率。若以(T1，Q1)作为工程设计值，可得出虽然历时未超过设定值，但仍有受灾的风险。

图11 洪峰、历时组合风险分布图Fig.11 Distribution of combined risk probability

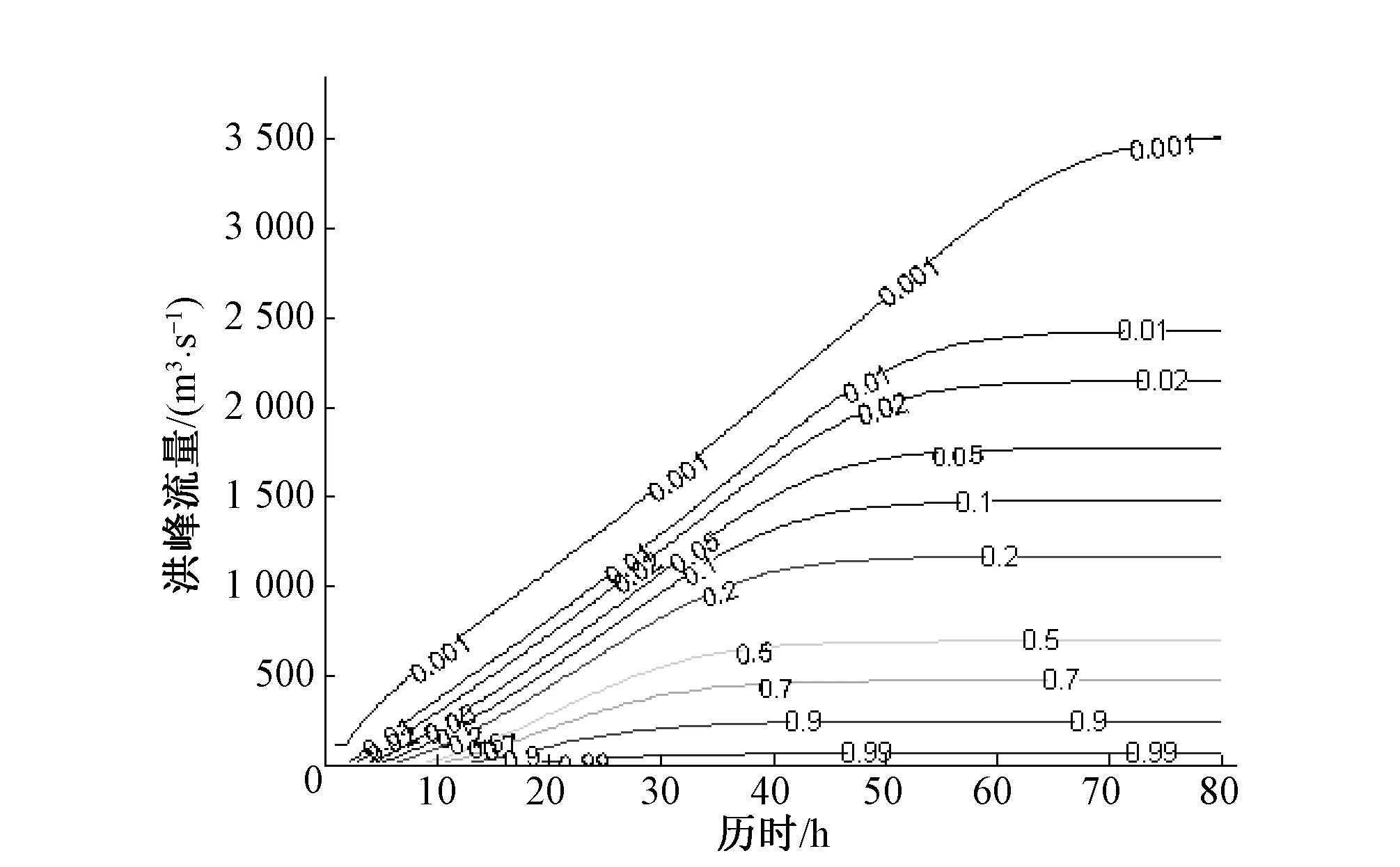
图12 洪峰、历时组合风险等值线图Fig.12 Contour of combined risk probability

由表6可以查出小于任一重现期的洪水历时下，遭遇不同洪峰流量的概率。可以看出，同频率下的洪峰与历时的组合风险率都远远低于单变量情况下的频率值，如两变量设计重现期为200 a和100 a一遇时，组合风险率分别为0.11%和0.21%，表明2变量在同频率设计情况下发生组合受灾风险的概率很低。同一重现期下的洪水历时与不同重现期下的洪峰流量组合频率随重现期的减小而增大，如洪水历时为200 a一遇时，洪峰重现期为100 a和10 a的组合风险率分别为0.5%和9.73%；而在洪峰流量重现期一定时，较短的洪水历时则对应较小的组合风险率，例如，当洪峰重现期为5 a一遇时，不同重现期的洪水历时所对应的组合风险率分别为19.41%、18.96%、18.20%、15.60%、12.59%、3.6%。由于从15.6%至3.6%有显著降低，可见5 a一遇洪峰对应的历时在31.7～40.2 h的可能性较大，且历时小于31.7 h时遭遇5 a一遇以上的洪峰概率较低。同理对于10 a一遇的洪峰，由于历时在45.0～52.3 h的组合风险率为8.37%～9.73%，变化幅度很小，可知历时在45.0 h以上的概率较小。另外，当历时重现期低于200 a一遇时，流域遭遇200 a一遇以上洪峰的概率极低。根据以上的分析结果，可以为洪峰历时遭遇组合概率的选取提供较为合理的科学依据。

表6 洪峰、历时组合风险率计算成果Tab.6 Rusults of combined risk probability

3 结论和展望

选取潖江河大庙峡水文站历年水文资料，从资料中提取洪峰流量与洪水历时的相关信息，分别以皮尔逊Ⅲ型和对数正态分布曲线建立了洪峰、历时的单变量分布函数，根据数据资料检验得到理论频率与经验频率基本相符。之后以AIC、OLS等进行拟合优度评价，建立了基于G-H Copula的洪峰与历时联合分布。通过比较在不同洪峰、历时组合情况下的单变量与2变量分布函数发现，后者可以更加全面地考虑洪水要素间的相关性，能更全面地反映洪水事件的整个过程，计算结果更为可靠，采用此方法进行工程规划时也更加安全，并且Copula函数对于边缘分布函数的无限制也大大增强了这种方法的实用性和拓展空间，对未来的水利工程设计有一定的参考价值，也为今后的多变量洪水频率计算研究提供了新的思路。

□

[1] 冯 平,崔广涛,胡明罡.暴雨洪水共同作用下的多变量防洪计算问题[J].水利学报, 2000,31(2):0 049-0 054.

[2] 谢 华，康英军，丁夏平.多特征变量洪水频率分析[J].灌溉排水学报,2012,31(6):11-14.

[3] 张 娜，郭生练，方 彬，等.暴雨事件中两变量联合分布研究[J].人民长江，2008,39(13):33-38.

[4] 侯芸芸. 基于Copula函数的多变量洪水频率计算研究[D]. 陕西杨凌:西北农林科技大学,2010:23-26.

[5] 谢 华，黄介生.两变量水文频率分布模型研究述评[J].水科学进展，2008,(3):443-452.

[6] D J Dupuis. Using Copulas in hydrology: benefits cautions and issues[J].Journal of Hydrologic Engineering, 2007,(4):381-393.

[7] G Salvadori C D Michele. On the use of Copulas in hydrology: theory and practice[J].Journal of Hdrologic Engineering, 2007,(4):369-380.

[8] 郭生练，闫宝伟，肖 义，等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文,2008,28(3):1-7.

[9] 刘和昌，梁忠民，姚 轶，等.基于Copula函数的水文变量条件组合分析[J].水力发电,2014,40(5):13-16.

[10] 闫宝伟，郭生练，郭 靖，等.基于Copula函数的设计洪水地区组成研究[J].水力发电学报，2010,29(6):60-65.

[11] 陈 璐，叶 磊，卢韦伟，等.基于Copula熵的神经网络径流预报模型预报因子选择[J].水力发电学报，2014,33(6):25-29.

[12] 杨志勇，袁 喆，方宏阳，等.基于Copula函数的滦河流域旱涝组合事件概率特征分析[J].水利学报，2013,44(5):556-561.

[13] Ganguli P, Reddy M J. Ensemble prediction of regional droughts using climate inputs and the SVM-copula approach [J]. Hydrological Processes, 2014,28(19):4 989-5 009.

[14] Sklar M. Fonctions de répartitionn dimensions et leurs marges[M] . Université Paris,1959- 08:229-231.

[15] Nelson R B. An introduction to Copulas[M]. New York:Springer, 1999．

[16] 杜 江，陈希镇，于 波.Achimedean Copula函数的参数估计[J].科学技术与工程，2009,(3):637-640.

[17] Christian Genest Anne一Catherine Favre. Everything you always wanted to know about Copula modeling but were afraid to ask[J].Journal of Hydrologic Engineering, 2007,(4):347-368.

[18] 宋松柏，康 艳，荆 萍.水文频率曲线参数优化估计研究[J].西北农林科技大学学报(自然科学版)，2008,36(4):193-198.

[19] 单国莉，陈东峰.一种确定最优Copula的方法及应用[J].山东大学学报(理学版)，2005,(4): 66-69.

[20] Cheng Wang, Ni-Bin Chang, Gour-Tsyhyeh. Copula-based flood frequency analysis at the confluences of confluences of river system[J].Hydrological Processes, 2009,(2):7 273-7 288.

[21] 张冬冬，鲁 帆，严登华，等.云南省干旱的时空演变规律及季节连旱的概率特征分析[J].应用基础与工程科学学报，2014,22(3):705-717.

[22] 史黎翔，宋松柏.基于Copula函数的两变量洪水重现期与设计值计算研究[J].水力发电学报，2015,(10):27-33.

[23] 李天元，郭生练，刘章君，等.基于峰量联合分布推求设计洪水[J].水利学报，2014,32(3):269-276.