闸坝式枢纽工程闸前导水墙体形优化研究

赵 晶，刁明军，赵 静，刘 斌，孙浩淼

(1.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065；2.四川省冶金设计研究院，成都 610065)

水利工程进水口段常因为体形边界不合理使得进水口前水流条件差并伴有漩涡，从而对闸室段的安全运行产生威胁。从以往工程进水口的布置经验表明，优化进水口导水墙体形布置是改善水流条件的一种有效方法。王玄[1]、王均星[2]等人研究溢洪道导水墙时采用了贴合水流曲线的导水墙，一定程度上改善了水流条件，为工程积累了宝贵经验。而对于闸坝式枢纽工程，通过选用合适的导水墙体形布置，改善闸前水流流态，减少漩涡产生的研究还鲜有报道。而数值方法模拟复杂漩涡现象，由于漩涡中心位置不易确定，因而其自由水面的模拟是数模的难点之一。陈云良[3]等人运用k-ε[4]紊流模型和流体体积方法追踪自由水面模拟表面凹陷漩涡以及吸气漩涡等复杂水力现象，高学平[5]等人采用数值模拟方法研究了多种进水口孔口体形认为扩散段和整流段对孔口附近的流态起决定性作用。数值模拟方法在模拟复杂水流水力特性和体形优化方面积累了相当多经验。本文结合某闸坝式枢纽工程，选用数值模拟方法和模型试验验证的研究手段，研究了2种不同的导水墙体形对闸坝式枢纽闸前流态、漩涡产生、表面流场、横向水位差等的影响，从而选择能够解决工程水力学问题的体形布置。

1 数学模型

1.1 控制方程

该模型采用RNGk-ε紊流模型，控制方程如下。

连续方程：

(1)

动量方程：

(2)

k方程：

(3)

ε方程：

(4)

式中各变量的含义及取值详见文献[6]。

计算时选用流体体积法(VOF法)追踪自由面，VOF法能保持流体的体积分数在整个运输过程中的守恒性，在计算单元内，第q相流体的体积分数为αq，有3种情况[7]：αq=0，即单元内无第q相流体；0<αq<1表示单元内包含多相流体，且∑αq=1；αq=1表示单元充满第q相流体。体积分数的更新值依赖于相邻计算网格之间的体积分数值，所以VOF法很容易实现并行计算。采用VOF法追踪自由水面，对q相流体采用输运控制方程：

(5)

1.2 计算模型与边界条件

为了保证数值模拟结果与实际情况相吻合，建模时考虑了上游库区、导墙、冲沙闸、泄洪闸、护坦、海漫、下游河道(见图1)。模型电站首部枢纽采用闸坝式布置，工程正常蓄水位高程1 496.00 m，坝顶高程1 498.00 m，闸室底板高程1 473.00 m。图1中闸室段从左岸至右岸分别布置冲沙闸和1号、2号、3号泄洪闸，冲沙闸孔口尺寸为3.0 m×8.0 m(宽×高)、泄洪闸孔口尺寸为7.0 m×13.0 m(宽×高)，闸室段长40.0 m。闸室下游接60.0 m混凝土护坦，再接40.0 m海漫，其后为100 m长下游河道。库区模拟最大高程1 499.00 m，计算区域网格以结构化网格为主，空间网格采用非均匀网格，电站取水口位置为非结构化网格，由于闸前进水口到闸孔位置是本次模拟的重点研究区域，因此对该区域的网格进行了加密，网格间距设为0.3 m。上游库区和下游河道大部分区域网格间距为1.0 m，局部非重点关注区域网格为2.0～4.0 m，为提高网格质量且计算方便，对库区做了适当简化，总计算单元约为80万。

入流边界条件设为速度进口，给定进口处速度、湍流动能、紊动能耗散率等，河道出口处设为自由出流边界和空气压力出口边界，模型顶端空气进口设置为压力进口边界，壁面采用无滑移边界条件。

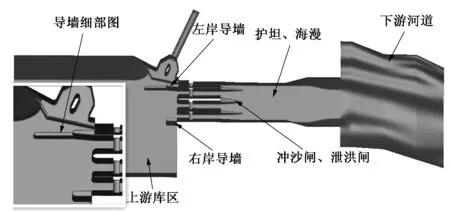
图1 数值模拟区域Fig.1 Area of numerical simulation

2 物理模型及研究工况

模型按重力相似准则[8]设计，模型比尺1∶40，为正态模型。模型模拟范围为坝轴线上下游分别为800和700 m，总共模拟原型长度1 500 m,模拟地形高程为1 500.00 m以下，下游模拟地形高程为1 490.00 m以下。全模型长约38 m。

数值模拟工况为校核工况，1 000 a一遇洪水，入库流量为3 620 m3/s，闸前20 m水位1 495.51 m，对应下游水位1 482.56 m，1号、2号、3号泄洪闸和冲沙闸闸门全开敞泄，该工况下电站不发电。

3 工程主要问题及优化方案

3.1 工程主要问题

闸坝式枢纽工程通常会采用闸前布置导水墙的方式优化进水口流态。原方案进水口处导水墙设计为：左岸2级导水墙相连，第1级长15 m、宽度3 m、高程为1 490.00 m，第2级长15 m、宽3 m、高程为1 485.00 m，具体布置见图2。

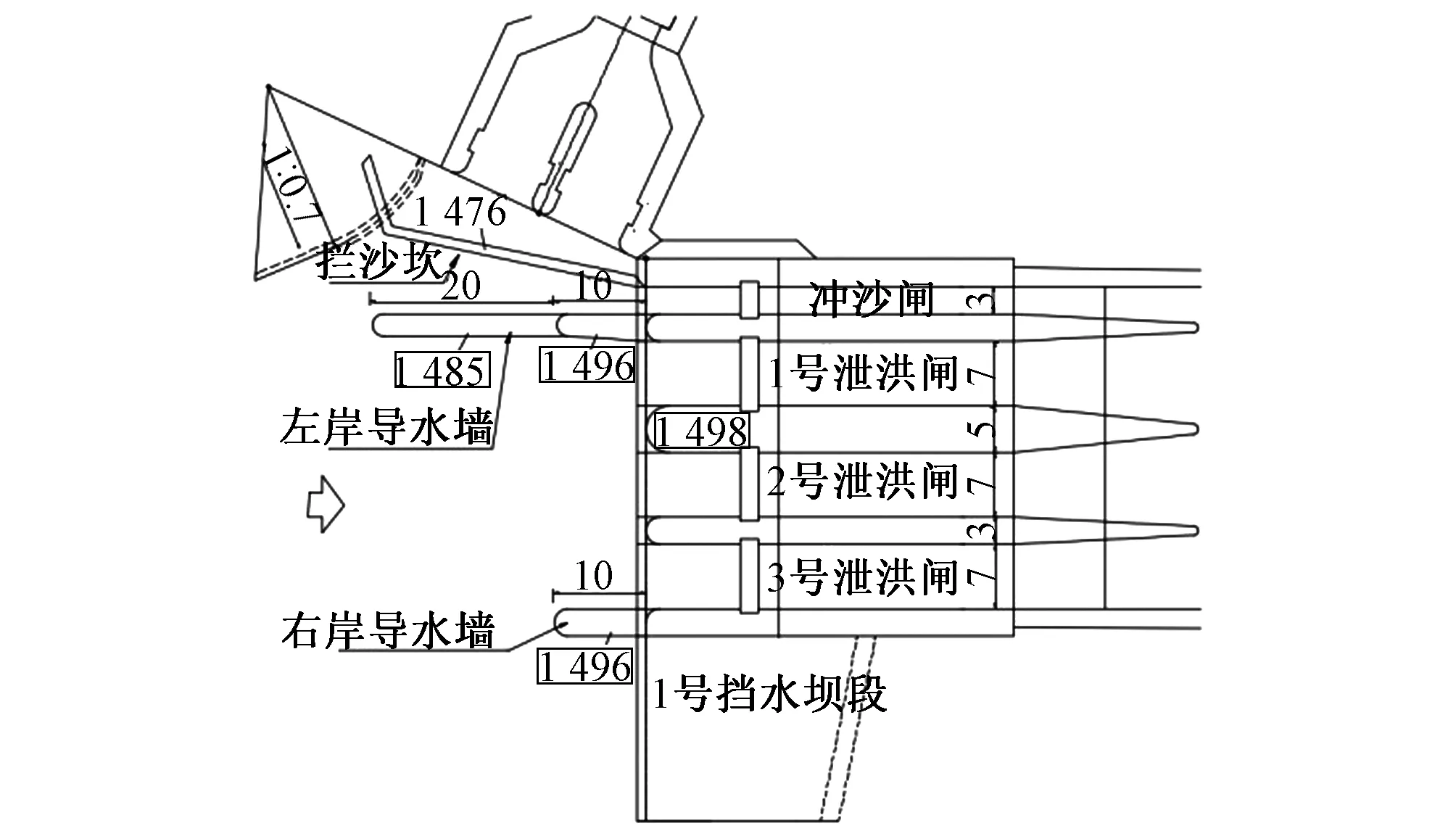
图2 原设计方案平面布置(单位：m)Fig.2 The floor plan for the original design

水流从宽阔的库区流向狭窄的闸孔时，过水断面突然收缩，再加上较大上下游水位差，闸前表面水体受较大下曳力[9]，水流有较大加速度，易使闸前水流处于复杂的三维流场中，水流紊动强烈，表面凹陷形成漩涡并产生吸气而引起闸门振动，对闸门的安全产生威胁。为了改善闸前进水口水流条件，经过多次数值模拟研究并结合物理模型试验，探索出一种新的导墙布置方案，可以有效解决上述问题。

3.2 优化方案

优化方案改为：左岸导水墙2级相连，第1级长10 m，为减少工程量宽度由3 m渐变为2 m，高程1 496.00 m，第2级长20 m、宽2 m、高程1 485 m，3号泄洪闸与挡水坝段连接处增加右岸导水墙，长10 m、宽3 m、高程1 496.00 m，闸室底板高程1 473.00 m，具体布置见图3。

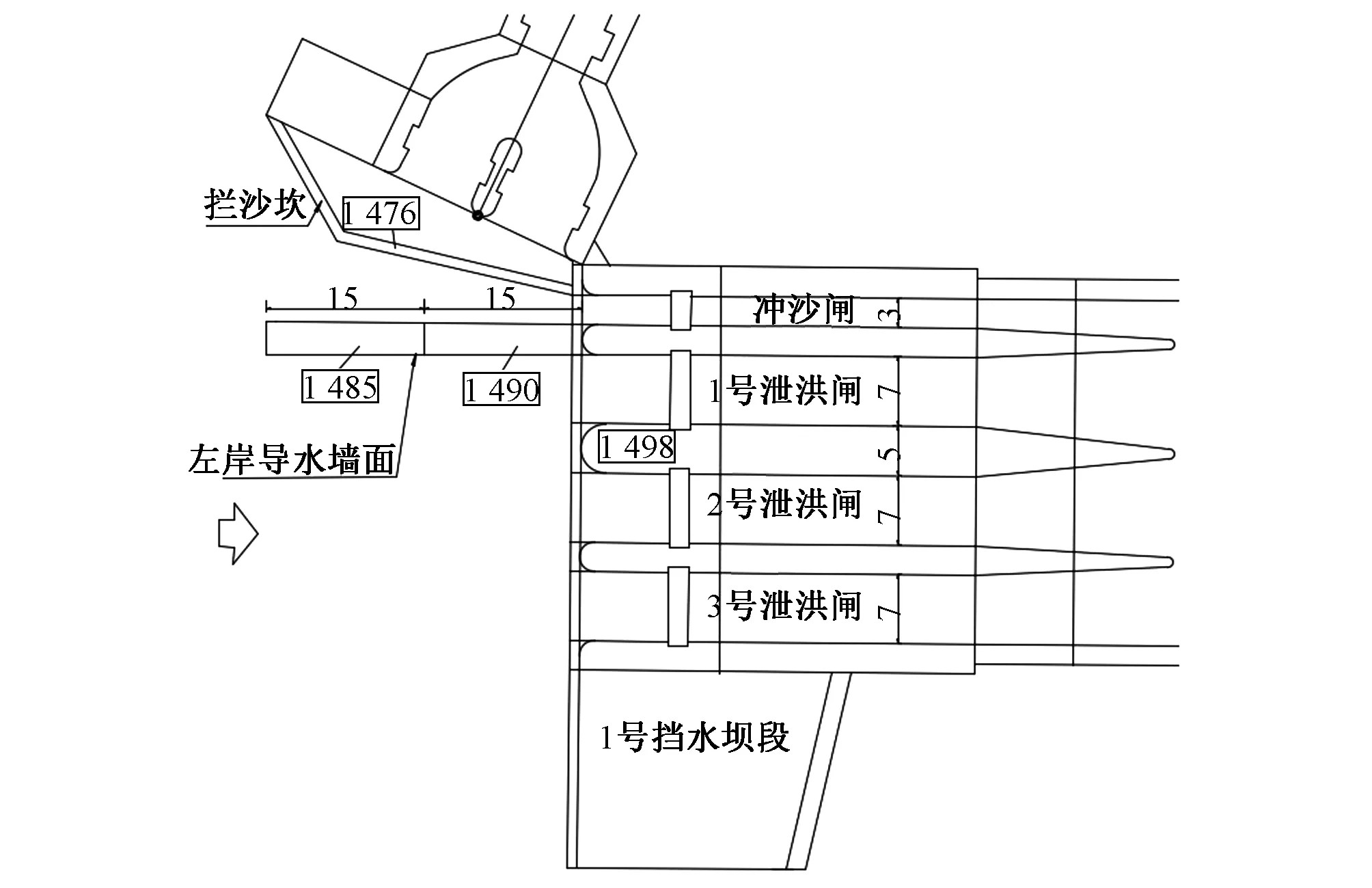
图3 优化方案平面布置(单位：m)Fig.3 The floor plan for the optimization scheme

4 计算结果与试验结果

4.1 计算验证

为了验证数值模拟的准确性，将优化方案闸前表面流速、闸前水位的数值模拟结果和模型试验结果进行对比，结果见表1。闸室底板高程为1 473.00 m，闸前水位计算的误差为水头误差。结果表明，误差小于3%，两者结果吻合良好，数值模拟结果可靠。

表1 优化方案闸前表面流速Tab.1 The surface flow velocity before the gate for optimization scheme

4.2 闸前流态

图4为模型试验得到的原设计方案和优化方案在1 000 a一遇工况下闸前流态对比图，图5(分别取高程1 490.00、1 493.00、1 494.00、1 495.00 m断面做成的闸前三维流线图)为数值模拟得到的原设计方案和优化方案水流内部三维流线对比图。由图4、图5可以看出：数值模拟与模型试验得到的闸前水流流态、漩涡分布和形态等参数吻合良好，优化方案中水流未见间歇性漩涡和明显脱壁现象。

图4 试验闸前水流流态Fig.4 The water flow regime before the gate of the test

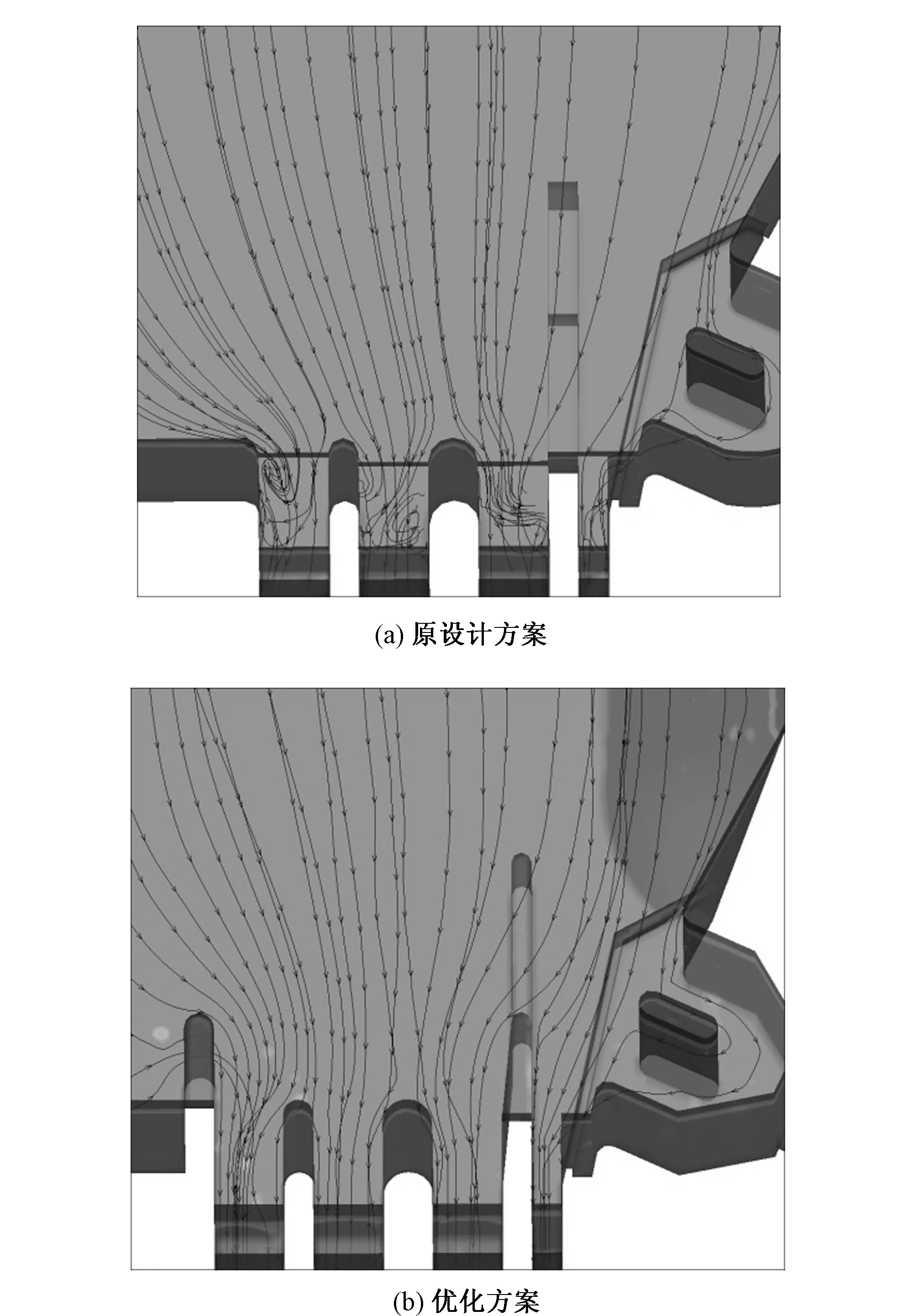
图5 试验闸前三维流线图Fig.5 The three dimensional stream lines before the gate of the test

按流体力学的观点，由边界不对称或不均匀流速等影响而产生的逆向梯度将诱发漩涡[10]。原设计方案：1号泄洪闸和3号泄洪闸边界条件极不对称，进水口处水流流态差，流速分布不均匀；1号泄洪闸由于导水墙的横向阻水作用，水流翻过第2级导水墙产生跌水并与上游来流和闸墩处绕流水体发生碰撞掺混，产生间歇性逆时针漩涡；3号泄洪闸由于右岸挡水坝段阻水作用，流线与闸墩交角较大，最大达到90°，流线发生较大转弯，水流产生明显脱离边壁现象，水面凹陷并伴有顺时针间歇性吸气漩涡，且有较大横向水位差；由于冲沙闸处闸孔宽度较小，泄流流量相对较小，流速相对均匀，水流条件较为良好。优化后方案：水流虽翻过左岸第1级导墙，但由于水流离闸孔较远，过流面积较大，库区的流速相对较小，水流较为平顺；水流经过闸前进水口时，左右岸导墙足够长，泄洪闸闸孔前边界条件较为对称，能较好地束水和调整水流流态，闸前流速分布较为均匀，闸前未见明显漩涡，水流未见明显脱壁现象并能较为平顺地流入闸室段。

4.3 闸前流场

图6为1 000 a一遇工况下原设计方案与优化方案在1 494.00 m高程处闸前表面流场图，通过对比可知：原方案流速在闸墩处迅速增大并伴有漩涡，局部流速达到6 m/s，水流能量高，伴有较大能量损失，优化方案流速分布更为均匀，横向流速更小，最大流速为5 m/s。

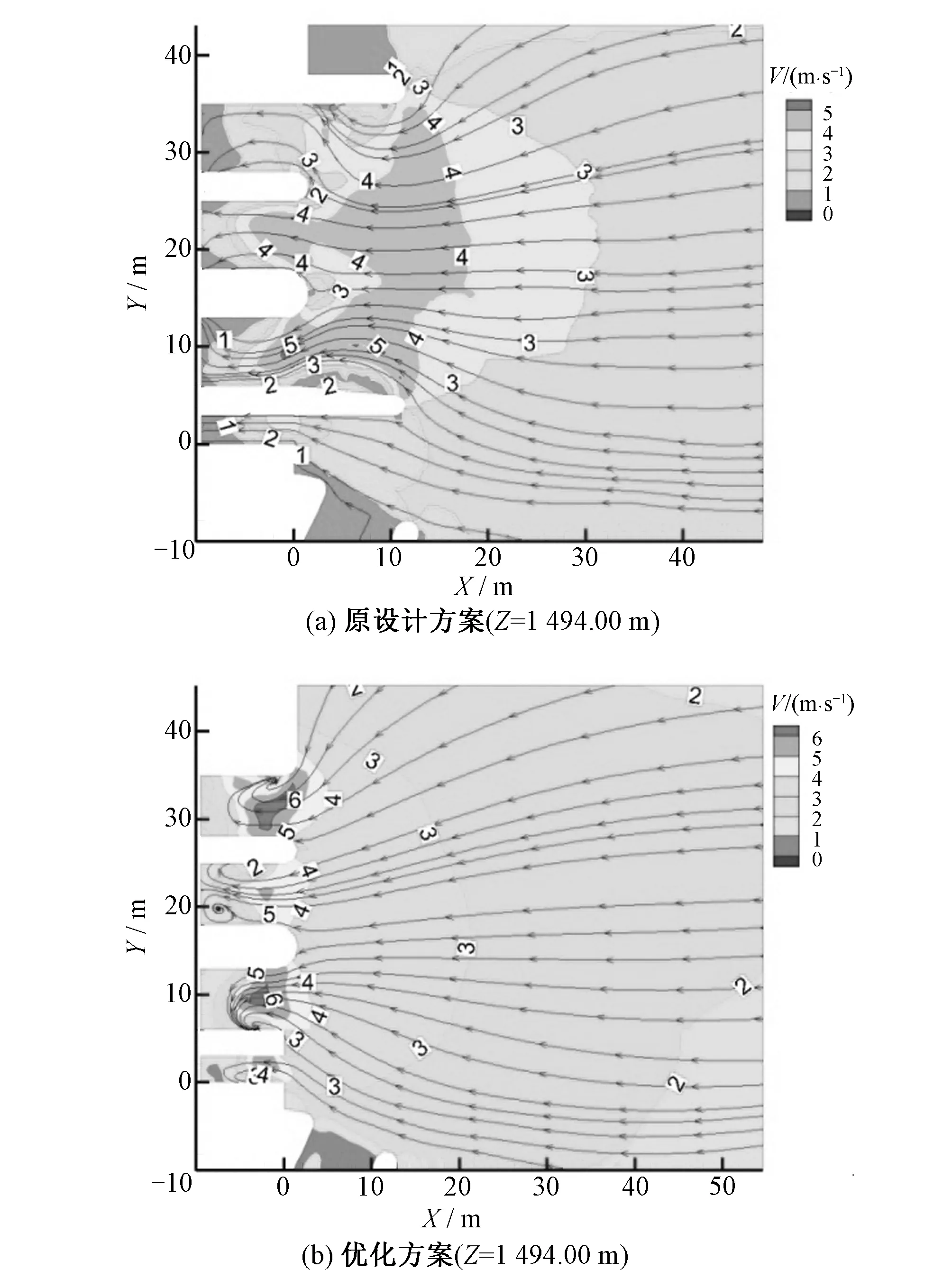
图6 闸前流场Fig.6 The flow field before the gate

原设计方案水流流经左岸导水墙之后，由于水体可以全部淹没导墙，导墙对河道的束窄作用不明显，近坝区水流流速均匀增大，水流到达闸墩处时，边界条件突变，水流过流面积突变减小，流速局部增大明显，达到4 m/s，接近闸孔处位置。由于边界条件、淹没水深等因素影响，漩涡中心处流速明显大于靠近边界处流速，漩涡区最大流速出现达到6 m/s。优化方案对导墙体形进行了改进，左岸第2级导水墙加高和右岸加导水墙之后，两侧导水墙束窄河床，水流流速增大，横向流速减小，流速分布均匀，水流较为平顺，当水流接近胸墙处时，水平方向流速减小，垂直方向流速增加，水体通过闸孔泄流。

4.4 横向水位差

闸前最大横向水位差是反映闸前流态和漩涡强度的重要依据之一。表2为原方案和优化方案在1 000 a一遇工况下计算和测量得到的闸前10 m内最大横向水位差对比结果。原设计方案得到的最大的横向水位差计算值和试验值分别为2.00、2.10 m，优化方案得到的最大的横向水位差计算值和试验值为0.72、0.63 m，且最大值都在3号泄洪闸。

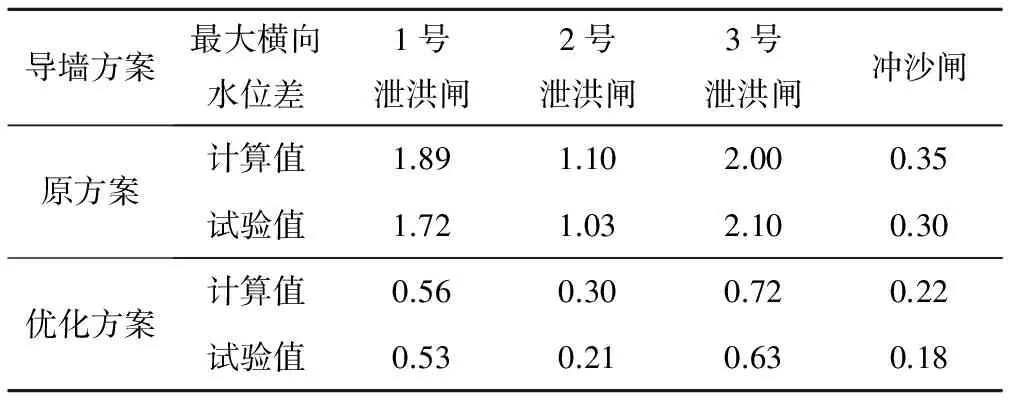
表2 闸前最大横向水位差 m

原设计方案：3号泄洪闸处边界条件变化最大，由于1号挡水坝坝段与闸孔轴线最大交角达到90°，此处水体产生脱壁且形成漩涡，导致该处横向水位差计算值达到最大值2.00 m；1号泄洪闸计算得到的横向水位差也较大，达到1.89 m。优化方案最大横向水位差较原方案明显减小，计算得到的最大横向水位差仅为0.72 m。结果表明：计算结果和实验结果吻合良好，数值变化规律基本一致；优化方案闸前最大横向水位差较原方案明显减小，水面基本持平，未见较大水位差，优化方案整体情况要优于原方案。

5 结 语

本文结合闸坝式枢纽工程实际，对该工程优化前后的2种闸前导水墙体型进行了数值模拟分析，并对计算结果进行了物理模型试验验证，得到了以下结论。

(1)本文采用的数值模拟方法可以较为准确地模拟得到水流流场、漩涡特征、横向水位差等，并能多方位观察水流内部流态，计算结果得到了试验结果的验证。该方法节约成本，便于多方案对比分析并选用合理体形布置，有较大的实用价值。

(2)通过2种不同导水墙体型布置条件的比较，得出了优化方案闸前水流的水力特性更具优势，结果满足工程设计要求，并且通过优化闸前导水墙体型可以起到以下作用：改善闸前流态、消除漩涡；改善流速分布、减小横向流速;减小最大水位差等。

(3)本文优化方案提出了一种新的导水墙体形布置。该体型布置使得闸坝式枢纽工程闸前进水口处边界条件更为对称，可以较好地改善闸前进水口处水流条件，该方案对于类似工程闸前导水墙体形设计具有指导作用。

□

[1] 王 玄，王均星，崔金秀.龙背湾溢洪道进水渠导水墙体型优化试验研究[J].中国农村水利水电，2009,(4)：100-104.

[2] 王均星，白呈富，李 泽，等.巴山水电站溢洪道导水墙体型优化试验研究[J].武汉大学学报(工学版)， 2005，38(4)：5-8.

[3] 陈云良，伍 超，叶 茂，等.水电站进水口水流流态的研究[J].水动力学研究与进展，2005，5(3)：340-345.

[4] Yakhot V，Orszag S A.Renormalization group analysis of turbulence: I basic theory [J].Journal of Scientific Computing，1986，1(1)：3-5.

[5] 高学平，叶 飞，宋慧芳.侧式进/出水口水流运动三维数值模拟[J].天津大学学报，2006，39(5)：518-522.

[6] 薛宏程，刁明军，岳书波，等.溢洪道出口斜切型挑坎挑射水舌三维紊流数值模拟[J].水利学报，2013， 44(6)：703-709.

[7] 邓 军，许唯林，雷 军，等. 高水头岸边泄洪洞水力特性数值模拟[J].水利学报，2005,(10)：1 209-1218.

[8] 吴持恭.水力学[M].北京：高等教育出版社，1982.

[9] 裴少峰，刘亚坤，倪汉根.闸前漩涡水力特性及形成条件的实验研究[J].水利与建筑工程学报，2012，10(5)：55-60.

[10] 郑双凌，马吉明，陈浩波，等.进水口漩涡特性及临界淹没水深的研究进展[J].南水北调与水利科技，2010，10(5)：129-132.