立方抛物线形断面收缩水深的直接计算研究
陈 诚,龚 懿,王 洁,严岳同,胡 璟
(1.扬州大学水利与能源动力工程学院,江苏 扬州 225009;2.宿迁水利枢纽管理局,江苏 宿迁 223800;3.江苏省洪泽湖水利工程管理处,江苏 洪泽 223100)
近年来,随着施工技术的不断发展,在渠道工程设计中已由原来单一的梯形断面向多元化形式发展[1],抛物线形渠道以其断面连续性好,易于计算和制作模型、水力及力学性能良好等优点在渠道衬砌与防渗工程中逐渐得到应用,其中以二次、立方和半立方抛物线形断面最为常见,其断面曲线方程的指数n分别为2、3和3/2。张丽伟和滕凯[2]、范子龙和赵明登[3]通过计算分别证明当n=3.35时,对应的最佳水力断面为抛物线类渠道的最优断面,因而立方抛物线形断面是最接近抛物线类渠道最优断面的一种常见的断面形式。
以往在明渠断面特征水深近似计算公式的推求过程中,通常是根据经验人为地选取函数模型进行逐次优化拟合,对于一些线型复杂的曲线,适合的函数模型往往很复杂[4-7],大大提高了模型寻找和求解的难度。为解决现有的立方抛物线形断面收缩水深计算公式[8-12]精度不够高的问题,同时避免复杂拟合函数模型寻找过程中存在的盲目性,本文提出明渠特征水深计算的迭代逼近-逐次优化拟合方法,拟通过迭代法和逐次优化拟合方法的联合运用直接推求高次方程的近似解析解,建立一套高精度的直接计算公式,为明渠特征水深直接计算方法的研究提供有益的参考。
1 无量纲收缩水深基本方程
如图1所示,立方抛物线形断面的曲线方程为:
(1)
式中:a为立方抛物线形断面的形状参数,m-2。

图1 立方抛物线形过水断面Fig.1 Cubic parabolic cross-section
根据水力学原理,由能量守恒方程推得的收缩水深基本方程为:
(2)
式中:E0为以收缩断面底部为基准面的过水建筑物上游总水头,m;hc为收缩断面处的水深,m;Q为过水流量,m3/s;g为重力加速度,通常取9.81 m/s2;φ为流速系数,一般取0.80~1.00;Ac为收缩断面处的过水断面面积,m2。
立方抛物线形渠道收缩断面处过水断面面积:
(3)
引入无量纲收缩水深x和无量纲参数k:
(5)
将式(3)、式(4)和式(5)代入式(2)并整理得:
(6)
式(6)即为关于立方抛物线形断面无量纲收缩水深x的基本方程。实际工程中,可根据式(5)通过已知参数求得k值,但无法由k对x直接进行求解。
2 直接计算公式的建立
2.1 迭代逼近-逐次优化拟合方法
本文提出高次方程近似求解的迭代逼近-逐次优化拟合方法,建立立方抛物线形断面无量纲收缩水深的精确计算公式。对式(6)进行简单的数学变换,可得如下迭代公式[8,10,12]:
(7)
式中:x0为迭代初值;xi为x0经i次迭代后得到的数值。
设迭代初值为x0,兼顾公式的精确性和简捷性,将其带入式(7)连续迭代3次,整理得:
(8)
式(8)实质上为一个迭代公式,在计算过程中需给定一个迭代初值计算公式由k计算x0的值,再将x0代入式(8)进行迭代计算。故(1-x0)3/8、(1-x0)9/642项均为常量。将除k和1外的7个常量作为未知的拟合参数进行逐次优化拟合,根据式(8)可得如下拟合函数模型:
(9)
实际工程中,一般取无量纲收缩水深x∈[0.01,0.50][8-11],每隔一定步长在该区间内给定一个x值,将其代入式(6)算得相应的k值,以式(9)作为拟合函数模型,运用Matlab 8.5软件的Curve Fitting Toolbox工具箱对所得的计算点进行逐次优化拟合,参照各参数的初始值反复进行参数率定,最终建立一套直接计算公式(拟合相关系数为1.000 0)。
(10)
2.2 现有的各类计算公式
目前相关水利专家学者共计提出5套立方抛物线形断面收缩水深的直接计算公式[8-12],均通过引入无量纲参数来计算收缩水深,其中赵延风等[10]公式和滕凯[11]公式是抛物线类断面收缩水深计算的通用公式,将n=3代入得到相应于立方抛物线形断面收缩水深计算的公式形式。各类计算公式具体见表1,其中λ、ψ、k′为计算过程中引入的中间变量,其他符号意义同前文所述。
3 误差分析与精度评价
3.1 本文公式的误差分析
为验证本文公式的精确性,在[0.01,0.50]区间内以一定步长选取不同的xi,以此作为无量纲收缩水深的精确值x*,将其代入式(6)算得与之相对应的k值,将k作为已知参数代入式(10),算得无量纲收缩水深的近似值x′,并根据式(11)计算相对误差δ(保留至小数点后第6位数字),计算结果见表2。即:
(11)
表2及进一步计算结果表明,在工程适用范围内,式(10)的最大相对误差绝对值仅为0.117 592%。以0.000 1为步长,计算式(10)相对误差曲线在[0.01,0.50]区间内的4 901个点的相对误差,分别取绝对值之后计算其平均值,得式(10)的平均相对误差绝对值为0.056 328%,误差小于0.1%的点占80.7%以上。本文将迭代逼近-逐次优化拟合方法用于明渠特征水深计算,建立的直接计算公式在工程适用范围内的相对误差均较小,具有很高的计算精度。

表1 现有的各类直接计算公式Tab.1 Presently available direct calculation formulae
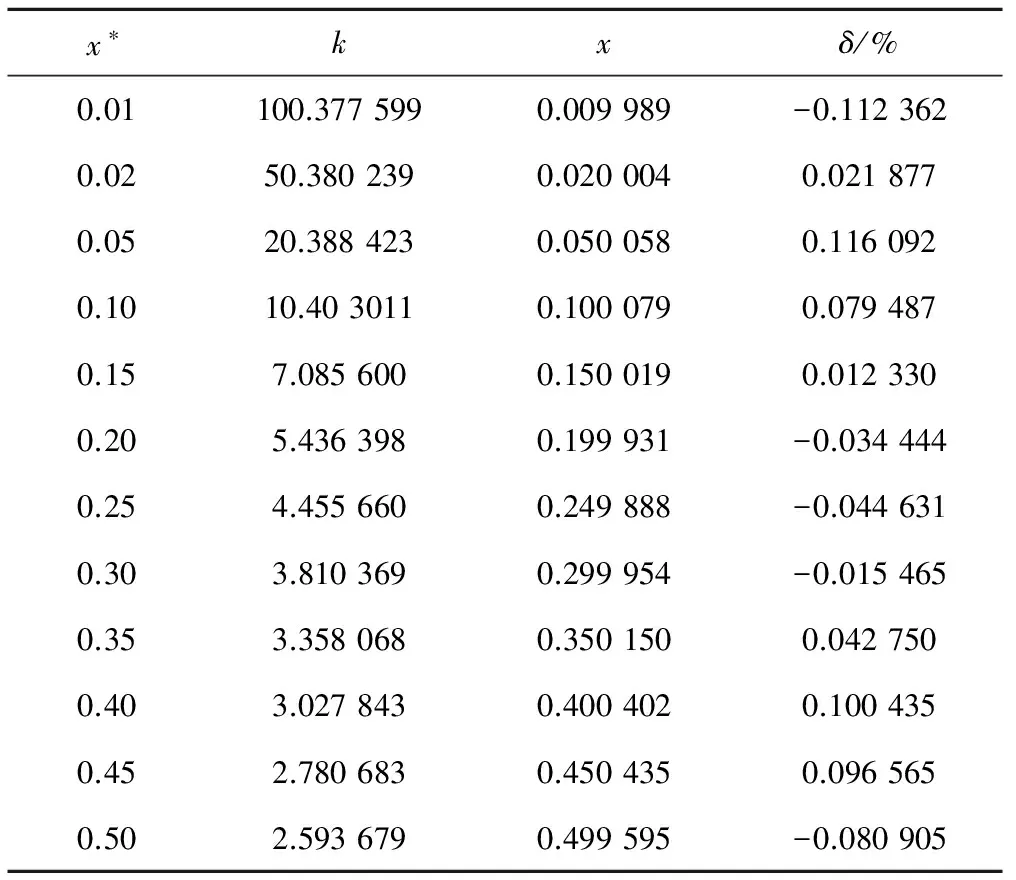
表2 本文公式相对误差分析Tab.2 Relative error analysis of the proposed formula
3.2 各类公式的精度评价
根据式(11),用同样的方法计算各类公式在[0.01,0.50]区间内的相对误差,并计算其最大相对误差绝对值和以0.000 1为步长的平均相对误差绝对值,计算结果见表3和图2。其中,图2绘制的是各直接计算公式和迭代初值计算公式的相对误差分布图,且略去相对误差绝对值大于1%的部分。

表3 现有计算公式相对误差Tab.3 Relative error analysis of the existing formulae
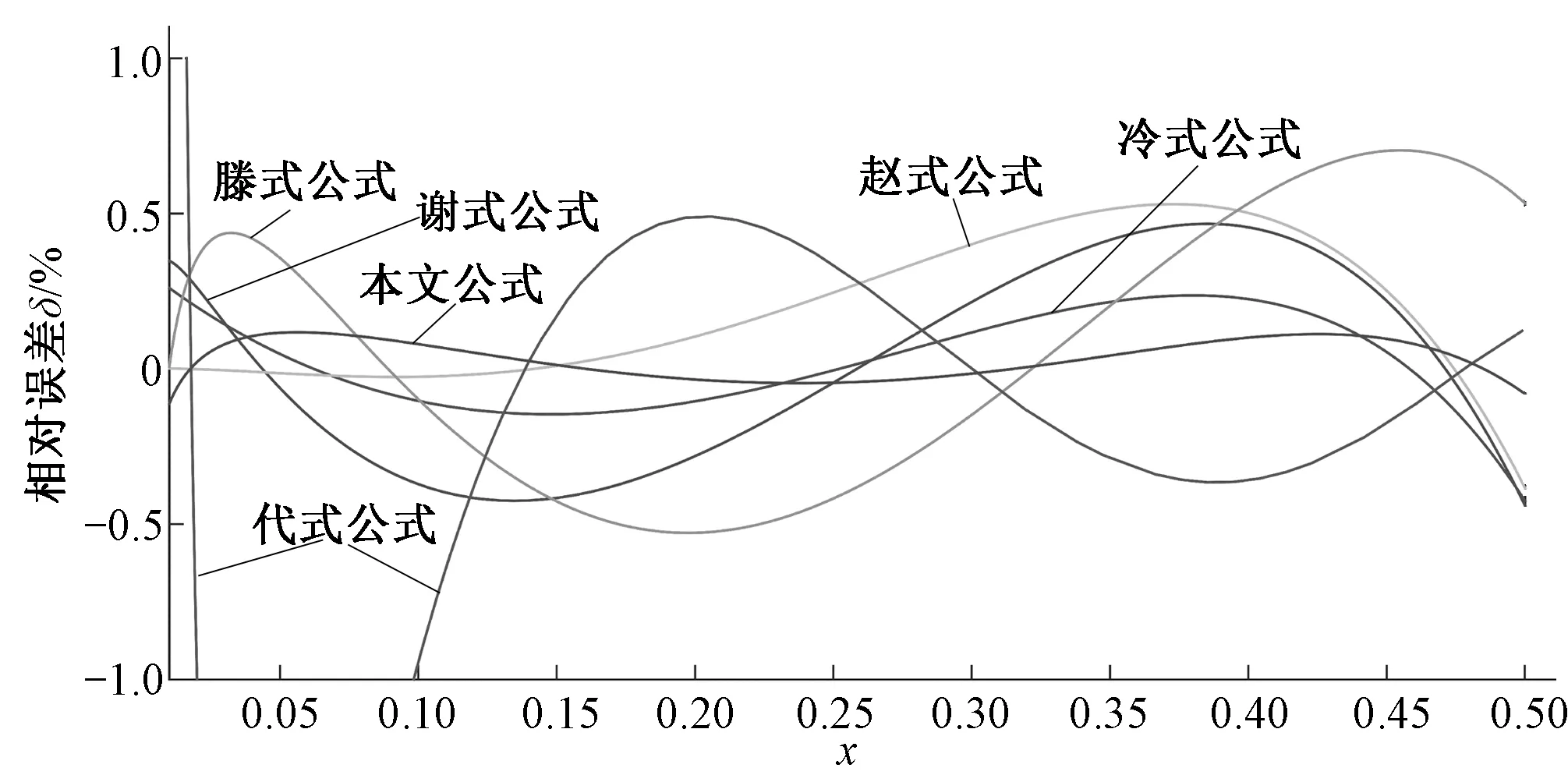
图2 各类公式相对误差分布图Fig.2 Distribution curve of relative errors of the existing formulae
根据表3和图2,当x∈[0.01,0.50]时,式(10)的最大相对误差绝对值小于现有的5套直接计算公式,比冷畅俭等[8]公式、赵延风等[10]公式和代述兵等[12]公式迭代1次的精度更高。本文提出的直接计算公式通过较小的计算量实现了立方抛物线形断面收缩水深的精确计算,体现出迭代逼近-逐次优化拟合方法在明渠特征水深计算中的优越性。
4 应用举例
选用与文献[8]、[9]相同的算例,已知某闸前断面总水头E0=15 m,通过渠道的流量Q=162 m3/s,流速系数φ=0.95,若采用立方抛物线形断面渠道,其断面曲线的方程为y=0.2|x|3,取重力加速度g=9.81 m/s2,求闸后断面收缩水深hc的值(保留至10-6m)。
(1)计算无量纲参数k。将已知参数代入式(5)得:
(2)计算无量纲收缩水深的近似值x。将k值代入式(10)有:
(3)计算收缩水深hc。将x值代入式(4) 计算hc:
hc=xE0=0.200 162 760×15=3.002 441(m)
通过试算法求得本算例收缩水深的精确值为3.003 480 m,相对误差仅为-0.035%,计算精度完全满足实际工程应用的要求。
5 结 语
本文提出高次方程求解的迭代逼近-逐次优化拟合方法,通过迭代算法和逐次优化拟合方法的联合运用直接推求高次方程的近似解析解,并将其运用于明渠特征水深的计算,建立了一套立方抛物线形断面收缩水深的高精度计算公式,在工程适用范围内其最大相对误差绝对值小于0.118%,较好地弥补了现有的各类直接公式及迭代初值计算公式精度不够高的问题,且计算较为简便,不需要通过反复的迭代过程提高计算精度。立方抛物线形断面明渠水力条件较优,本文直接计算公式的提出,可为该类渠道的设计和运行管理提供有益的参考。
本文提出的迭代逼近-逐次优化拟合方法具有一定的理论创新意义,通过迭代逼近的过程建立合适的拟合函数模型,参考各拟合参数的初始取值进行参数率定可保证参数求解过程的收敛,为高次方程的近似求解提供了一条新的思路,对各类断面明渠及隧洞的特征水深计算有一定的实用参考价值。在今后的研究中,需进一步考虑如何通过迭代逼近的过程较好地建立拟合函数模型,以及如何合理地选取拟合参数用于曲线拟合,从而提高计算精度。
□
致谢:感谢扬州大学水利与能源动力工程学院院长程吉林教授和副院长吉庆丰教授在论文写作过程中给予的悉心指导和帮助。
[1] 张志昌,贾 斌,李若冰,等.抛物线形渠道的水力特性[J].水利水运工程学报,2015,(1):61-67.
[2] 张丽伟,滕 凯.抛物线形断面最优水力参数及方程指数计算方法[J].水利水电科技进展,2014,34(5):65-68.
[3] 范子龙,赵明登.幂律形水力最佳断面设计与正常水深计算方法[J].中国农村水利水电,2015,(9):157-159.
[4] Vatankhah A R.Direct solutions for normal and critical depths in standard city-gate sections[J].Flow Measurement and Instrumentation,2012,28:16-21.
[5] Zhang X Y,Wu L.Direct solutions for normal depths in curved irrigation canals[J].Flow Measurement and Instru-mentation,2014,36:9-13.
[6] 张新燕,吕宏兴.无压圆形隧洞正常水深直接算法[J].水力发电学报,2014,33(1):127-131.
[7] 张新燕,吕宏兴,朱德兰.U形渠道正常水深的直接水力计算公式[J].农业工程学报,2013,29(14):115-119.
[8] 冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31,35.
[9] 谢成玉,滕 凯.三次抛物线形渠道断面收缩水深的简化计算公式[J].南水北调与水利科技,2012,10(1):136-138.
[10] 赵延风,王正中,刘计良.抛物线类渠道断面收缩水深的计算通式[J].水力发电学报,2013,32(1):126-131.
[11] 滕 凯.抛物线形断面渠道收缩水深简化计算通式[J].水利水电科技进展,2014,34(5):61-64.
[12] 代述兵,刘韩生,卞晓卫,等.三种抛物线形断面收缩水深的直接计算公式[J].长江科学院院报,2015,32(9):90-93.

