蓄能机组同步起动过程暂态建模及仿真

罗 胤，靳国云，常玉红，王小军，李建光，郝国文

(1．河南天池抽水蓄能有限公司，河南南阳 473000 2.国网新源控股有限公司，北京 100761)

随着抽水蓄能(以下简称“蓄能”)机组在电力系统中的比重不断增加，其对电网的影响已不可忽略。蓄能机组具有起动灵活，工况转换多变的特点，因此起动问题在蓄能电站运行中占有极其重要的地位。同步起动(背靠背起动)作为蓄能机组电动工况的主要起动方式之一[1-5]，也引起了诸多电力学者的重视。同步起动是耦合了动力、机械、电气3种时变非线性系统相互作用的复杂过渡过程[6]，还需通过仿真和试验对其精确分析和验证。电力工作者已对蓄能机组同步起动稳态运行工况进行了大量详尽的分析，该过程的物理意义十分清晰[7-9]，但该过程暂态分析的文献还不多见。有人认为：蓄能机组同步起动过程频率低、电压低，短路电流自然小，这种观点并不完全正确。电力系统电磁和机电暂态理论为开展蓄能机组同步起动过程的分析工作提供了有力支持。

1 蓄能机组同步起动过程

1.1 起动过程简介

蓄能机组同步起动是用本电站或者相邻电站的一台常规发电机组或蓄能机组作为发电机运行来起动其他蓄能机组。起动过程见图1。首先建立电气轴，合上拖动机组的拖动闸刀(SBI2)、被拖动机组的被拖动闸刀(SBI1)、拖动机组出口开关(GCB)，分别合上2机组励磁开关，并保持恒励磁电流；再开启拖动机组导叶，当驱动转矩大于阻力转矩时，2机组转速缓慢上升；最后被拖动机组满足同期要求并网，解除2机的电气轴，停下拖动机组。

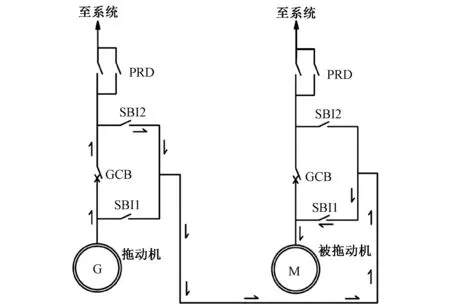
图1 蓄能机组同步起动过程示意图

1.2 数学模型

该过程精确的数学模型已经建立[10-12]，其模型的基本形式见图2。指导思想是用派克方程将a，b，c坐标系统下的变量转换为d，q，0坐标系统下的新变量，使时变参数变换为常参数，按正弦变换的交流量变为恒定的直流量；在d，q，0坐标系统下分别建立拖动机和被拖动机的电压、磁链方程；建立拖动机和被拖动机的转子机械运动方程；找出同步起动过程中拖动机和被拖动机电压、电流接口关系方程；共同联立可得到一个12阶的状态方程：

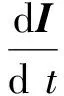
I=[IGd,IGq,IGf,IGD,IgQ,ωG,δG,IMf,IMD,IMQ,ωM,δM]T

U=[0,0,UGf,0,0,TGm/HG,0,UMf,0,0,-TMf/HM,0]T

式中：A和B均为12×12的系数矩阵，A和B矩阵中具体元素略。可对系统状态方程组求解，获得蓄能机组稳态同步起动过程中的各项状态变量。

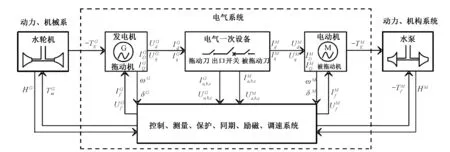
图2 蓄能机组同步起动模型

2 同步起动过程暂态建模和分析

蓄能机组同步起动过程中可能发生机组出口突然短路故障，由于整体供电回路的负载突然消失以及突然短路时的次暂态、暂态过程[13]，使回路中的电流突增；另一方面，在短路后瞬间电动机由于惯性保持转子转速不变，且励磁电势不会消失，供给短路点第2路电流，增大该回路的短路电流水平。为了保证在同步起动过程中电气设备的可靠运行，必须计算短路电流最大瞬时值；同时，机组电气参数在低频工况下与工频工况不同，短路电流也不同，因此有必要通过仿真计算，确定机组在同步起动过程中，不同频率下各种故障电流的大小。

2.1 同步起动过程机组出口发生三相短路的分析

同步起动过程中，2台电机的电压、频率并不恒定，但在暂态分析过程中，考虑到转子惯性较大，短路暂态过程又是在很短的时间内完成，因此在分析时可近似认为转子转速不变，励磁电压不变。在分析三相短路时应用叠加定理和拉氏变换方法。同步电机的短路问题分为正常稳态运行[见图3(c)]和故障分量[见图3(d)]2种情况。同步起动过程水泵采用压水起动方式，拖动机组带负载很小，认为电磁暂态过程中磁路不饱和，文献[13]给出了dq0坐标系中的发电机线性常系数微分方程(派克方程)，这里不再赘述，只对同步起动过程中定子回路进行分析。电压方程和磁链方程为：

(1)

Φd=XdId+XadIf

Φq=XqIq

(2)

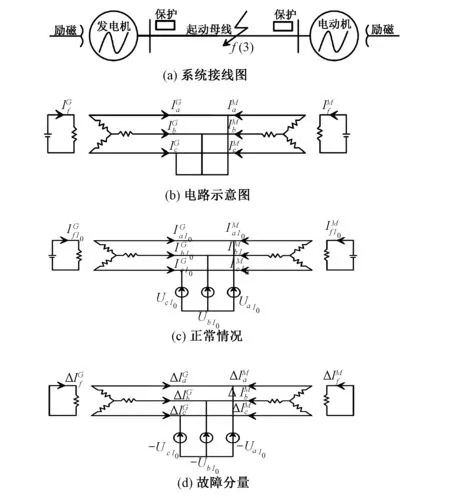
图3 同步起动三相短路分析

正常运行时的稳态电流计算如图3(c)，拖动机内电势超前被拖动机内电势的相角为δ，即为功角。则在dq0坐标下，拖动机的电压方程为：

(3)

结合式(1)、(2)、(3)可以解出电流Id，Iq如下：

(4)

由于拖动机和被拖动机之间是背靠背联在一起，2台电机之间的端电压和电流皆相同，则有式(5)，通过该式可以解出被拖动机组正常运行时的电流：

(5)

故障分量分析见图3(d)，在突然短路时励磁电压不变，当电枢端突加一个与短路前的端电压大小相等但方向相反的三相电压。电枢d，q绕组端分别突然加上-Ud0、-Uq0时，电压方程式由式(1)、(3)得：

(6)

当电枢端突加电压-Ud0、-Uq0时，励磁绕组相当于短路，可以得到相应的电枢磁链，代入式(6)后可以得到电压与阻抗、电流的关系式。当电枢端突加电压时，各绕组的电流、磁链的初值为零，经拉式变换并进行解析后，可得到故障分量的电流。将稳态电流和故障分量电流叠加得到同步起动过程三相突然短路的电流为：

(7)

在dq0坐标系统下的电流求出后，再返回实际的a、b、c坐标系统，即Ia=Idcosθ-Iqsinθ，假定t=0时，d轴与q轴的夹角为θ0，则θ=t+θ0，代入式(7)，整理后得：

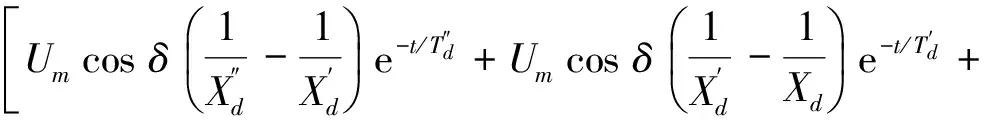
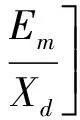
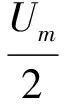
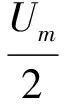
(8)

将式(8)中的θ0置换θ0-120°和θ0+120°，即可得到Ib和Ic。从式(8)分析，突然三相短路后，定子各相短路电流由周期、非周期及2倍频分量构成。从物理意义上理解，当定子绕组突然三相短路后，由于转子磁场的旋转及定子绕组中产生相应的三相稳态基频电流，将引起定、转子各绕组中的磁链突变。为阻止各闭合回路中磁链不发生突变，定子绕组、转子阻尼和励磁绕组中就产生了非周期电流。由于转子以同步速度旋转，转子阻尼和励磁绕组中的非周期电流会在定子绕组中产生相应的基频周期电流分量，即暂态分量和次暂态分量。由于转子绕组中存在电阻，突然短路在转子绕组中引起的非周期电流将逐渐衰减至零，由转子绕组中的非周期电流在定子绕组中感生的暂态分量和次暂态分量电流亦按同样时间常数衰减。同样的，定子绕组中的非周期电流会在转子绕组中产生相应的基频周期分量电流，但由于转子不对称，这个转子绕组中的基频电流所产生的磁场相对转子而言可分为2个转向相反，转速均为同步转速的分量，其中转子转向相同的旋转磁场对定子的转速为2倍频，它将在定子绕组中引起倍频周期分量。由于定子绕组存在电阻，定子绕组中的非周期电流和倍频电流将逐渐衰减至零。

由式(8)可知，各电流分量的幅值主要由故障前运行电压Um与同步电抗Xd、暂态同步电抗X′d、次暂态同步电抗X″d之比以及定子激磁电动势Em与同步电抗Xd的比值决定，考虑到拖动机组带负载很小，认为定子激磁电动势和故障前运行电压相差不大，同时考虑到现有大型蓄能机组在同步拖动前，2台机组均已投入励磁，并且采用恒定励磁电流方式，则由式Em=IfXad可知，Em正比于Xad。文献[14]给出了磁路不饱和情况下纵轴电枢反应电抗与角频率是正比关系，即Xad正比于频率f。所以，同步起动过程中，2台电机虽然需要经历一个较长的低频过程，且机组和起动母线的电抗参数随频率不断变化，但定子激磁电动势也随频率同步变化，2者相互抵消导致2者之比变化不大，即短路电流幅值与工频工况下短路电流幅值相差不大。

2.2 同步起动过程机组出口发生两相短路的分析

两相短路时，定子电流也包含基频交、直流分量。与三相短路不同，基频交流分量三相不对称。对于不对称短路，考虑用对称分量法确定其相量形式的对称分量，在分析过程中发现两相短路电流没有零序分量，而正、负序分量大小相等，方向相反。定子电流中基频负序分量在气隙中产生以同步转速与转子旋转方向相反的磁场，它与转子的相对速度为2倍同步速，并在转子绕组中感生2倍基频的电流，进而产生2倍基频脉动磁场可分解为2个按不同方向旋转的磁场。与转子旋转方向相反而以2倍同步速旋转的磁场与定子电流基频负序分量产生的旋转磁场相对静止；顺转子旋转方向以2倍同步速度旋转的磁场，将在定子绕组中感生出3倍频的正序电动势，这组电动势将在定子电路中产生3倍基频的三相不对称电流。而这组电流又可分解为3倍基频的正、负分量，负序电流产生的磁场在定、转子绕组中形成新的高次谐波分量。这种不断相互作用的结果是：凸极机两相突然短路时，短路电流中含有一系列的高次谐波，这些高次谐波分量和基频正序分量一样衰减。

2.3 同步起动过程机组出口发生三相短路故障1台机组灭磁开关拒动

同步起动过程中若机组发生故障，要求拖动机组和被拖动机组灭磁开关同时动作以切断供给故障点的2路电源，但国内外多家蓄能电站的实际运行经验表明，蓄能机组在同步起动调试阶段可能发生由于计算机运算和信号传输问题导致2台机组灭磁开关动作时间不一致，即一台机组的灭磁开关切除时间可能滞后甚至出现灭磁开关拒动[15,16]。同步起动过程机组出口发生三相短路故障之后，2机电气轴被切断，2机分别向短路点供给电流，灭磁开关先切除的一侧，由于转子磁场迅速减弱，其短路电流衰减很快，灭磁开关后切除或是拒动的一侧定子电流衰减很慢。

3 仿真试验

在Simulink仿真平台上利用国内某4×300 MW蓄能电站给定的相关参数搭建了包括水轮机输入、励磁输入、发电电动机、起动母线、水泵负荷在内的详细仿真系统模型，机组的参数见表1。

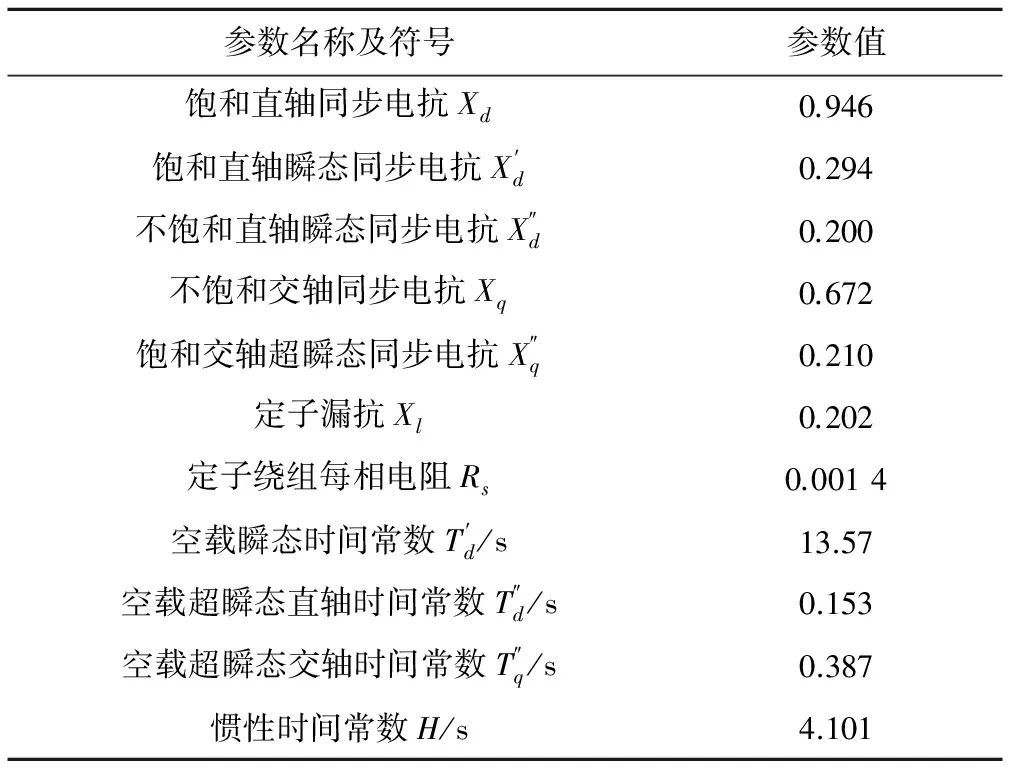
表1 300 MW抽水蓄能机组相关参数

表1给出的为该蓄能机组基频下的相关参数，但基于以上建立的同步起动过程稳态和暂态数学模型，仿真过程无论处于何种频率运行，均可根据模型自行计算出机组相关参数在该频率的大小，仿真模型具有一定的自适应性。

3.1 同步起动稳态运行过程仿真与试验

在同步起动稳态模型的基础上，利用2台300 MW蓄能机组进行起动过程仿真，得到拖动机和被拖动机的转速上升曲线见图4(a)。实际用2台300 MW蓄能机组进行同步起动试验，得到起动试验过程中2台机组转速上升曲线见图4(b)。

通过对比仿真和试验曲线：仿真过程35 s后2机组开始加速，由零转速上升至99%转速时间约为250 s，斜坡加速时间约为215 s；实际起动过程斜坡加速阶段时间为210 s，2条曲线的趋势一致，仿真和实测结果比较吻合，仿真模型可用于蓄能机组同步起动。

3.2 同步起动过程机组出口三相短路仿真

由图4(a)的同步起动稳态仿真转速上升曲线，可以得到故障瞬间拖动机和被拖动的转子转速，即故障瞬间起动母线上电流的频率。在同步起动仿真条件相同的情况下，设置在起动过程中不同时刻发生三相短路故障，得到短路电流的大小与波形见表2。

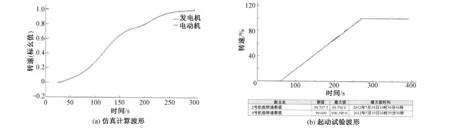
图4 同步起动转速上升曲线

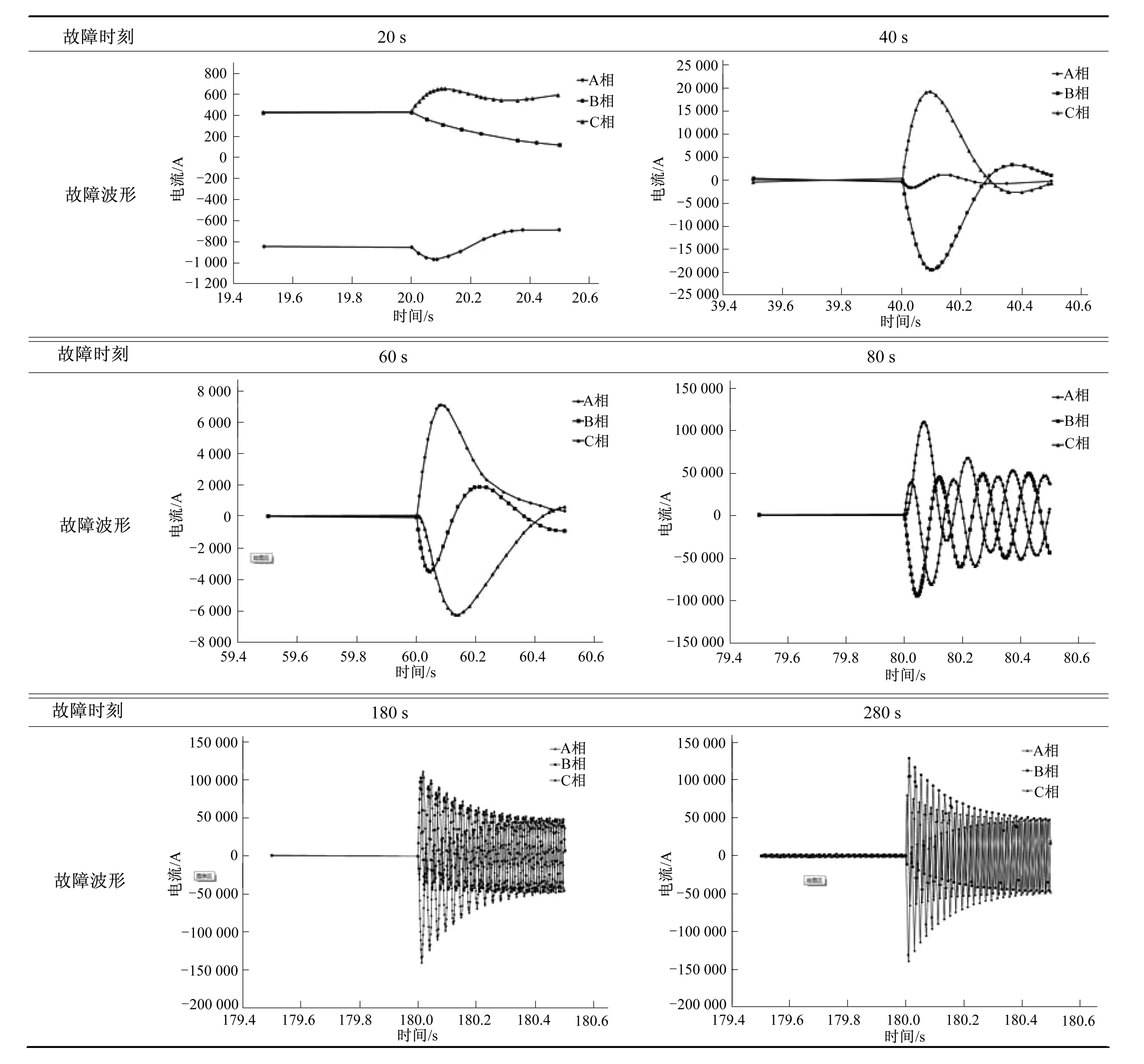
由表2可知，短路电流逐渐衰减，冲击电流在短路发生后半个周期时出现，由20、40和60 s时刻发生短路电流波形可以看出，当2机还未旋转或转速很低时，短路电流很小且以直流分量为主，一旦2机开始加速，短路电流会迅速增加，比较80、180和280 s时刻发生短路故障的电流波形可知，同步加速阶段发生故障时短路电流幅值变化不大，这与前面的理论分析吻合。为了更直观看出短路电流和频率的关系，统计了不同频率下短路冲击电流和短路电流周期分量幅值见表3，绘制成曲线见图5。

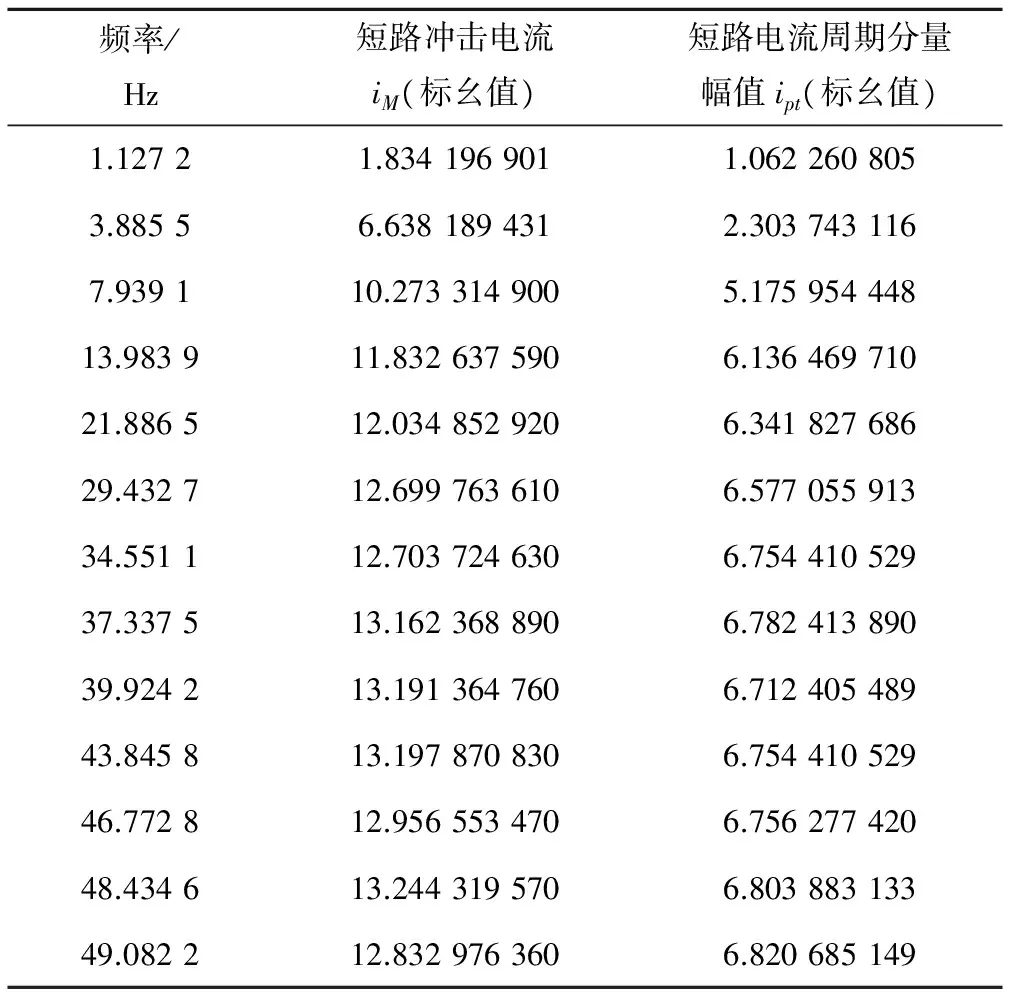
表3 不同频率下短路冲击电流幅值和周期短路电流幅值

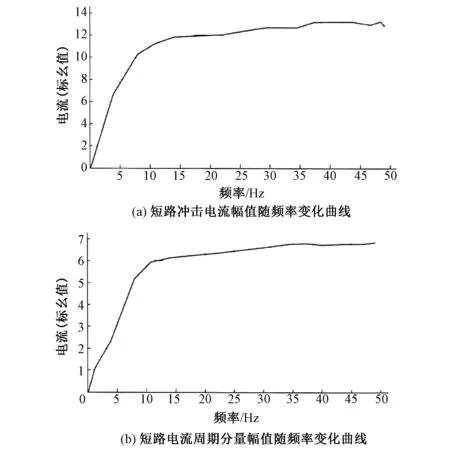
图5 三相短路电流随频率变化曲线

由图5可知，同步起动过程中，尽管处于低频、低压状态，但发生故障时低频短路电流的峰值和有效值与机组正常运行情况下发生故障时工频短路电流的峰值和有效值基本接近，尤其是在稳步加速阶段(10～50 Hz)短路电流基本趋于稳定，与正常运行情况下的短路电流大小、幅值基本一致。而当机组处于极低频率阶段(0～10 Hz)短路电流幅值虽然较小，但故障电流随着频率上升而迅速上升。

3.3 同步起动过程机组出口两相短路仿真

在同步起动仿真条件相同的情况下，设置在起动过程中不同时刻发生两相短路故障，得到短路电流的大小与波形见表4。

由表4可知：两相短路故障后，故障两相的短路电流基本大小相等，方向相反，非故障相电流略有上升，同步加速阶段发生故障时短路电流幅值变化不大。由于凸极机两相短路时，其定、转子的不对称性，电流中含有一系列高次谐波，在仿真计算的过程中取两相短路后一个周波的A相短路电流的频谱进行分析，图6为180 s时刻发生两相短路时的频谱。

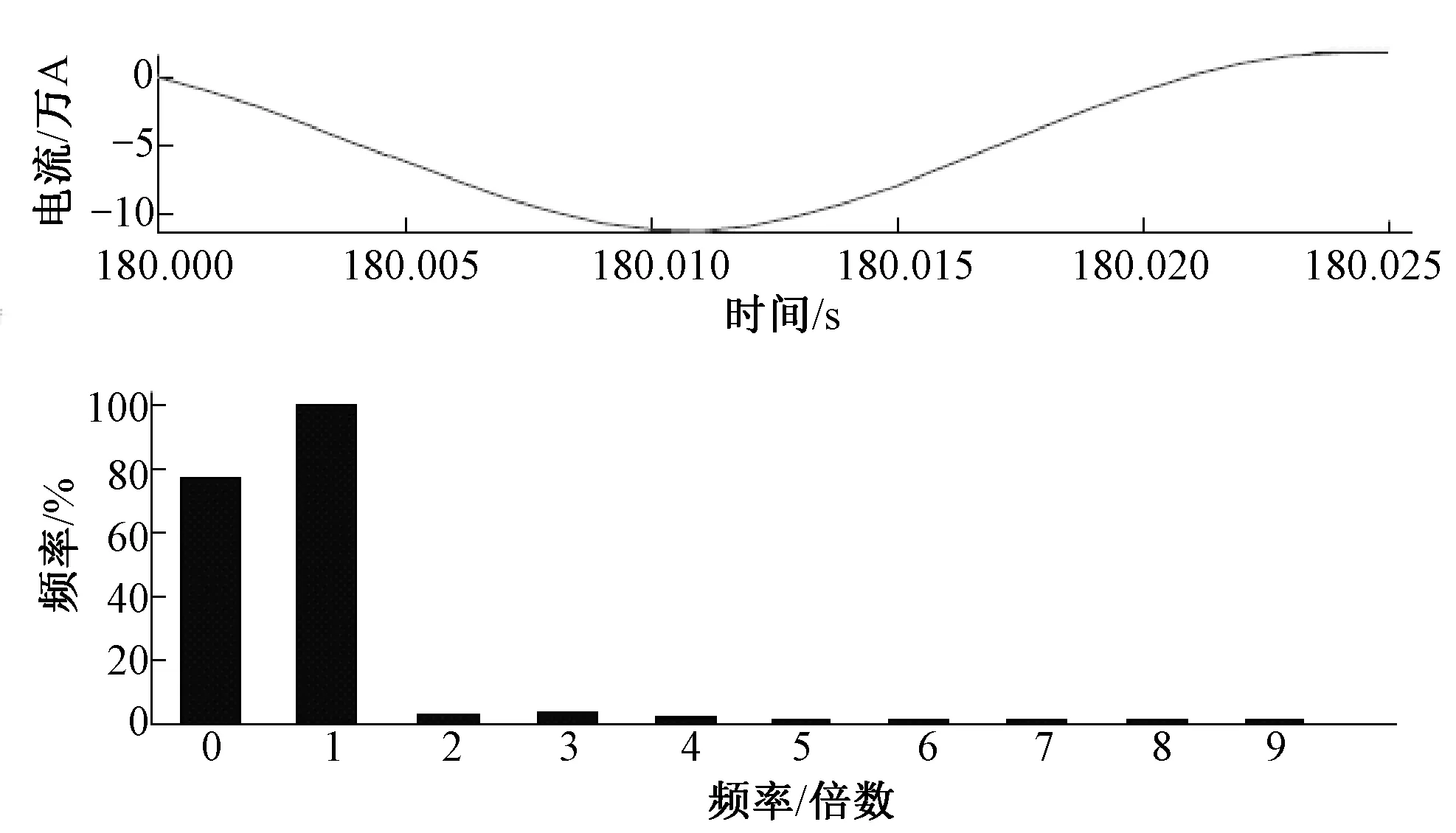
图6 180 s发生两相短路故障A相电流的频谱分析图

图6表明在180 s发生两相短路故障时，波形畸变率并不是很高，约为5%，故障电流仍然是以直流分量和基波为主。两相短路冲击电流幅值及周期分量随频率变化规律与三相短路仿真结果相同，这里不再进行赘述。

3.4 同步起动过程机组出口三相短路后1台机组灭磁开关拒动仿真

根据现场对继电保护装置时间特性测试，继电保护装置最短动作时间也需15 ms，而从保护开出到开始逆变灭磁的时间大约为12.496 ms。仿真模拟在机组出口180 s时发生三相短路故障，故障之后延时大约15 ms断开发电机的灭磁开关，电动机的灭磁开关拒动而未跳开，得到故障电流波形见图7。

切除灭磁开关的一侧短路电流迅速衰减，在故障1.5 s以内衰减至安全区域，而灭磁开关拒动时，短路电流虽有衰减趋势，但衰减很慢，5 s之后回路中仍存在较大电流。同理，仿真模拟发电机灭磁开关拒动的情况，计算出灭磁开关拒动侧定子电流的大小与图7(b)大致相同。

若出现故障状态下一台机组灭磁开关拒动的情况，但机组出口开关(交流开关)的低频遮断能力有限，一般在0～25 Hz不允许直接切除，现场可考虑采取以下措施：首先可设置独立的硬布线联跳回路，同步起动过程中，一台机组灭磁开关跳闸，另一台机组灭磁开关必须联跳；其次，增设次同步过流保护或低频过电流保护，且采用相应的电流加速判据，出现故障时，加速跳开2机灭磁开关，切断故障电源。

4 结 语

基于同步电机的电磁和机电暂态理论，建立了蓄能机组同步起动过程中的暂态模型。对蓄能机组同步起动过程中的稳态和暂态过程进行了仿真，最终得出同步起动过程中两机发生故障时的短路电流大小与低频、低压状态关系不大。希望这个结论能够为蓄能机组设备制造厂商提供一种理论依据，能够为设计单位进行蓄能电站一次设备的选型和短路电流的计算提供帮助。

表4不同时刻机组出口两相短路电流

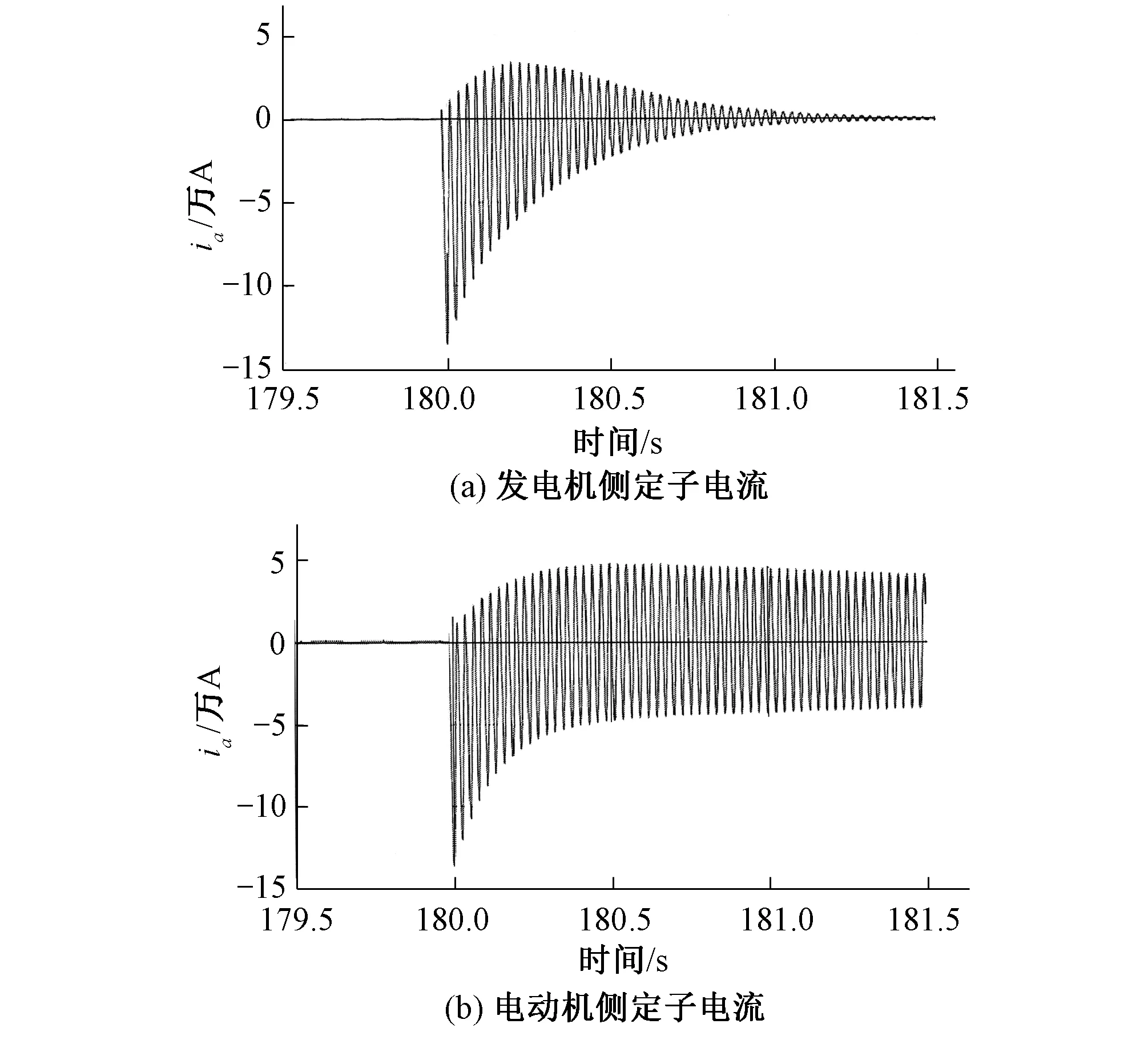
图7 电动机侧灭磁开关拒动时2台机组定子电流

□

[1] 梅祖彦.抽水蓄能发电技术[M].北京：机械工业出版社，2000.

[2] 姚晴林，祖 伟，赵玉乃.抽水蓄能电站机组的起动方式及其低频特性对保护的影响[J].继电器，1996，24(3)：10-15.

[3] 田立军，陆于平，陈 珩.抽水蓄能电动发电机启动过程数字仿真[J].电力系统自动化，1997，21(7)：38-41.

[4] 罗 胤，郭建彪，黄 倩，等.蓄能机组换相对差动保护的影响分析[J].电气应用，2014，33(21)：77-80.

[5] 罗 胤.一起蓄能机组核相过程电压异常分析[J].高压电器，2013，49(12)：88-94.

[6] 邵宜祥，吕宏水，冯 永.抽水蓄能机组背靠背启动规律的仿真[J].水电自动化与大坝监测，2008，32(4)：5-9.

[7] 骆 林，马志云.抽水蓄能电动发电机组背靠背起动过程仿真研究[J].大电机技术，2005，(6)：11-15.

[8] 高金玲，林宪枢.抽水蓄能电站背靠背起动问题的研究[J].空冷汽轮发电机的通风系统设计，1998，(4)：22-25.

[9] 邓玉章.抽水蓄能发电机组背靠背启动的研究[J].东方电气评论，2004，18(1)：15-18.

[10] 李光琦.电力系统暂态分析[M].北京：中国电力出版社，2006.

[11] 戈宝军，王自涛，黄晓瑞.同步电机背靠背起动精确数学模型及其分析[J].电工技术学报，1999，14(3)：21-25.

[12] 王自涛，戈宝军，黄晓瑞.抽水蓄能电机背靠背启动过程的计算机仿真[J].哈尔滨理工大学学报，1999，4(3)：41-44.

[13] 李光琦.电力系统暂态分析[M].北京：中国电力出版社， 2006.

[14] 马志云.电机瞬态分析[M].北京：中国电力出版社，1998.

[15] 常永亮，张兵海，王 勇，等.抽水蓄能机组背靠背启动中跳闸技术改造方案[J].水力发电，2011，37(7):34-36.

[16] 杨光华，栾德艳，常 颖，等.浦石河抽水蓄能电站发变组继电保护的设计及特点[J].水力发电，2012，38(5)：75-77.