基于改进遗传算法的水库群水质水量优化调度研究
张 杰,冯民权,王 钰
(1.西北旱区生态水利工程国家重点实验室培育基地,西安 710048;2.山西水利职业技术学院,山西 运城 044004)
近年来,随着水环境污染的日益严重,人们对水质提出了更高的要求,水库的调度任务由传统的水量调度逐渐转变为水质水量统一调度,水质水量联合调度已成为水库调度的研究前沿和热点[1],但对于水库群的水质水量联合调度仍然存在困难,即多水库、多目标及约束条件复杂的问题,不同水库不仅上下游之间存在复杂水力联系,同时还承担着生活、工业、农业、生态等不同部门的水量水质要求,决策变量巨大、约束条件复杂成为统一联合优化调度的障碍[2-5]。鉴此,提出改进的遗传算法对流域水库群进行水质水量优化调度研究。
1 水质水量联合优化调度模型
1.1 目标函数
水量目标:
(1)
式中:Djkt为区域在第j分区第k用水部门第t时段的需水量;Gijkt为区域第i个水库给第j分区第k用水部门第t时段的供水量;ajk为第j分区第k用水部门优先得到供水的重要程度系数;J为分区总数;K为用水部门总个数;T为时间段总划分数量;I为水源总数目。
水质目标:
(2)
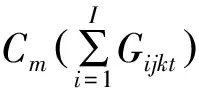
1.2 约束条件
1.2.1 水库水量平衡约束
(1)串联水库水力关系:
Vi+1,t=Vi+1,t-1+WRi,t+WBi,t-Yi,t-WOi+1,t
(3)
式中:Vi+1,t为串联水库第i+1水库第t时段末的蓄水量;Vi+1,t-1为串联水库第i+1水库第t-1时段末的蓄水量;WRi,t为串联水库第i水库第t时段的下泄水量;WBi,t为串联水库第i水库与第i+1水库间第t时段的区间产水量;Yi,t为串联水库第i水库与第i+1水库间第t时段的区间用水量;WOi+1,t为串联水库第i+1水库第t时段的出库水量。
(2)并联水库水力关系:
Vi,t=Vi,t-1+∑WRi,t+∑WBi,t-∑Yi,t-WOi,t
(4)
式中:Vi,t、Vi,t-1分别为并联水库中第i水库第t、t-1时段末的蓄水量;∑WRi,t为并联水库中邻近第i水库所有上游分支水库第t时段的下泄水量总和;∑WBi,t为并联水库第i水库与邻近第i水库的所有上游分支水库间第t时段的区间产水量总和;∑Yi,t为并联水库第i水库与邻近第i水库的所有上游分支水库间第t时段的区间用水量总和;WOi,t为并联水库第i水库第t时段的出库水量。
1.2.2 水库水位约束(含防洪要求)
(1)非汛期:
Zi,死≤Zi,t≤Zi,正
(5)
(2)汛期:
Zi,死≤Zi,t≤Zi,汛
(6)
式中:Zi,死为第i水库的死水位;Zi,t为第i水库第t时段末的水库水位;Zi,正为第i水库的正常蓄水位;Zi,汛为第i水库的汛限水位。
1.2.3 河段水量平衡约束
WSl,t-WMl,t+WQl,t-WOl,t=Vl,t-Vl,t-1
(7)
式中:WSl,t为第l河段首断面第t时段的过水量;WMl,t为第l河段末断面第t时段的过水量;WQl,t为第l河段第t时段的区间水量;WOl,t为第l河段第t时段的用水量;Vl,t、Vl,t-1分别为第l河段第t、t-1时段末的蓄水量。
1.2.4 河段控制断面水位约束
Zl,n最低水位≤Zl,n,t≤Zl,n警戒水位
(8)
式中:Zl,n最低水位为第l河段内第n个控制断面的允许最低水位;Zl,n,t为第l河段第n个控制断面在第t时段的河道水位;Zl,n警戒水位为第l河段内第n个控制断面的警戒水位。
1.2.5 需水量约束
(9)
式中:Dmin,jkt为区域在第j分区第k用水部门第t时段的最小需水量;Gijkt为区域第i个水库给第j分区第k用水部门第t时段的供水量;Dmax,jkt为区域在第j分区第k用水部门第t时段的最大需水量。
1.2.6 输水通道过水能力约束
(10)
式中:Gijkl为区域第i个水库给第j分区第k用水部门第t时段的供水量;Uj为第j子区渠道的过水能力。
1.2.7 水质指标约束
(11)
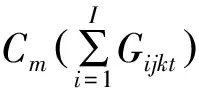
1.2.8 非负约束
2 改进遗传算法的设计
2.1 改进算法设计基本思路
在大量的计算中发现,多水库、多目标的水质水量联合调度模型的可行解域由连续的可行域和许多不连续的小可行域组成,可行域的不连续性经常会导致在寻优过程中产生破坏约束的个体,进而寻优陷入重复循环中而降低算法效率[6],而小可行域边界附近的非可行域对可行域边境的寻优起着一定辅助作用,故在搜索过程中不可只偏重可行域,因此对非可行解而言,关键在于度量其对约束条件的违反程度。为此提出将遗传算法分步进行,并且每步加入不同的罚函数,使其在复杂的区域内快速收敛到最优解。
(1)第1步。满足约束算法,采取直接比较比例法(DCPM法)针对水库群调度的约束条件来搜索可行解域。给复杂的约束条件引入一辅助罚函数,来衡量个体不满足约束条件的程度大小,在引入辅助函数前先将所有等式约束条件化为hj(X)=0形式,将所有不等式约束条件化为gj(X)≤0形式,在此基础上,定义函数:
(12)
式中:X=(x1,x2,x3,…,xn)∈Rn是n维实向量;gj(X)为不等式约束;hj(X)为等式约束,共有m个约束,其中有q个不等式约束。
引入上述罚函数,对每一个体进行处理后都会有一不满足约束条件程度值viol(X),根据DCPM法的筛选原则[7]对个体进行的选择。
(2)第2步。目标优化算法,引入小生境遗传算法的思想[8],这一步是在第1步基础上提高对可行域的局部搜索能力。根据水库群调度的精度要求,需定义一个衡量2个个体之间相似程度的值D,通过与任2个个体间的海明距离L作比较来进行遗传到下一代。若L≤D,则表明个体间相似度较大,则对适应度较小个体施加一个较强惩罚项,增大其淘汰几率;若L>D,表明个体间相似度小或不在同一可行域内,需要保留参与下一代优化运算。
2.2 改进算法的实现
2.2.1 编码的选择
水库群水质水量联合调度问题中,决策变量多,二进制编码下染色体长度过长,寻优的可行空间巨大,而浮点编码在此情形下会有较强的鲁棒性,运算效率较高,编码方式选择浮点编码[9]。
将出库水量组合序列作为优化个体,设供水部门数为K,时间尺度划分时段数为T,供水区域划分数为J,水库数目为I,根据浮点编码规则,水库出库水量在调度精度的要求下的可行范围内生成的个体为:
(W11,W12,…,W1n,W21,W22,…W2n,…WI1,WI2,…,WIn)
n=JKT为每个水库的决策量个数,则每个个体的基因长度为nI。
2.2.2 适应度函数的设计
在水库群水质水量联合调度中,需要对目标函数进行适当的尺度变换,由于是水质水量两个目标,根据水质目标函数中的水质指标响应函数,水质指标可转换为水量指标,同时将水质指标约束转换为水量约束,在转换后的水量区间与需水约束区间之间取交集,得出综合需水区间,在此基础上就可转换为单目标进行优化。经过多次试验,将指数变换形式与线性变换相结合的形式,找一个较大数Cmax与目标函数进行转换:
(13)
由此可得Cmax取值为JKT。
则适应度函数的指数变换形式为:
H(G)=abc/[1+F(G)]
(14)
通过实际计算调试,可得变换参数的取值为:a=100,b=15,c=10。
2.2.3 改进算法基本步骤
第1步:
(1)初始化种群P(0)、代数 ,并计算其适应度值和H及其不满足约束程度值V。
(2)t=t+1,根据DCPM法的筛选原则筛选出种群P′(t),再根据交叉变异算子可得群体P(t)。
(3)计算群体中P(t)不可行解的比率η,并控制其比率,每隔一定代数自动调整ε值,并返回(2)。
(4)根据H值和V值,对最后一代排序并标记M个个体,记为PM(t)。
第2步:
(1)初始化代数t=0,令P(0)=PM(t),并进行降序排列,标记前N(N (2)t=t+1,通过遗传算子得出群体P(t)。 (3)将第1步的群体PM(t)与第2步第(2)步群体P(t)合群,并根据小生境算法原则进行筛选,得到群体P′(t)。 (4)计算群体P′(t)中个体的H值,并依据H值进行降序排列,标记前N个个体。 (5)终止条件判断。相对误差范围或规定的代数如果不满足,转到(2),若满足,输出结果。 选择洪汝河流域进行实例分析,洪汝河流域地处河南省西南部,与安徽阜阳接壤,在淮河流域上游王家坝北岸,是淮河平原向低山丘陵的过渡地区。流域水系主要包括小洪河、汝河及臻头河3大河流,其中小洪河与汝河在班台交汇,流入大洪河,属于淮河的2级支流。该流域内主要大型水库工程有石漫滩水库、板桥水库、薄山水库和宿鸭湖水库4座,为多年型调节水库,在流域内呈串—并联型。4座大型水库的主要水库特征见表1。 根据流域地形与污染源调查,大多工业污染源集中在河流中上游地段,而流域上游水库水属优质水,在水库经河道给流域供水时,容易造成污染。 表1 洪汝河流域各个水库特征Tab.1 Characteristics of different reservoir in Hongru River basin 水利工程所承担的供水对象包括有驻马店地区的市、县10个及平顶山地区县城2个,为了反映每条河流水质情况,分别选取了庙湾断面、遂平断面、夏屯断面以及河坞断面作为水质控制断面,将洪汝河流域系统概化,概化图见图1。 图1 洪汝河流域概化图Fig.1 Generalized figure of Hongru River basin 通过对实例模型进行程序调试可知,算法中个别参数对寻优的结果影响较大。在DCPM法中,非可行解的比率η对计算效率影响比较明显,若比率η定得太高,则程序长时间在非可行解域内循环,降低运算效率,根据经验选择η=0.05~0.2;在小生境算法中,衡量个体间的相似程度值D决定了小生境算法的局部搜索能力的大小,D取值范围并不能准确地确定出优化结果,而是当参数在一定的取值范围内时,优化结果在某个范围内出现的概率较大。从表2中可知,参数D在范围100~180中取值时,总供水量要比其他范围的更大。 表2 不同参数D范围内优化结果的最有可能范围Fig.2 The most probable range of different parameters D to optimize the results 通过以上分析,具体的参数选取如下。 (1)第1步。群体规模选择100,最大遗传代数为100代,自适应交叉概率和变异概率取值范围本别为[0.4,0.9]、[0.001,0],非可行解比率η=0.05~0.2,不满足约束程度阈值 的大小影响非可行解的比率,与水库出库水量有关,其初值根据实际调度来确定,根据非可行解的比率大小每隔5代进行自动调整一次。 (2)第2步。种群数量为100,最大遗传代数300~500代,交叉概率与变异概率范围同第1步,标记的代数N取50~80,小生境参数D取100~180,后期罚函数参数选取10-30。 以1997-2006年10 a系列来水资料及污染物源的排污资料为基础,根据各分区、各部门的需水情况,对洪汝河流域进行了水质水量联合优化调度。水质污染物选取化学需氧量(COD)及氨氮(NH3-N)来进行分析。具体结果见表3、表4。 表3 洪汝河流域各水库供水方案Tab.3 Different reservoir water supply schemes in Hongru River basin 注:由于农村生态需水量很小,所以归并到了农村生产需水量中。 表4 洪汝河流域各水质控制断面水质改善成果Tab.4 Water quality improvement result of different waterquality control sections in Hongru River basin 为表明本文改进算法的有效性,将改进的算法与实际模拟的效果及其他类型遗传算法[8]作了计算比较,给出了其他算法下的水库总供水量及各个水质断面对应的COD浓度和NH3-N浓度及其改善程度,结果详见表5、表6。 表5 不同优化算法下的供水方案Tab.5 The reservoir water supply schemes ofdifferent optimization algorithms 表6 不同优化算法下的水质改善成果Tab.6 The water quality improvement result ofdifferent optimization algorithms 从表3的供水方案与表5的实况模拟方案进行比较以及从表4的水质改善结果可知,供水方案得到了较大的优化,并且控制断面的水质也得到了相应的改善,进而表明本文提出的改进遗传算法成功的对洪汝河流域的水量水质进行了联合优化调度。 通过表3、表4与表5、表6的结果对比分析表明,本文提出的改进遗传算法相较其他优化算法而言,不仅在供水方案上的总供水量要优于其他方案,而且在水质方面的改善程度也大于其他优化算法的结果,表明了该算法在优化调度中的有效性。 从算法的运算效率来看,改进算子算法遗传代数1 000代,自适应算法的代数多达2 000代,而本文算法的代数最大值600代,运算效率得到了较大的提高,总体表明本文的改进遗传算法在水库群水质水量优化调度中适用性较高,比文中提及的其他优化算法更高效、稳定。 在求解水库群水质水量联合优化调度模型中,上下游水库群水力联系复杂,决策变量指数级增长,可行解空间急剧扩大,鉴此提出改进遗传算法,对部分关键非可行解域作了适当选择进行寻优计算,并对可行域空间进行分步优化。该改进算法应用于洪汝河流域水库群水质水量联合调度中取得了较好的结果,水库群调度方案优化明显,水质得到了较大改善。与其他类型遗传算法作了优化比较,该改进算法具有更高的优化效率、稳定性和实用性。本文算法发展前景较好,具有一定的通用性,在理论上有一定创新,但分步进行增加了算法的复杂性,并且在参数的研究与选择中依然存在一定的问题,今后需要在此基础上进一步探讨。 □ [1] 董增川,卞戈亚,王船海,等.基于数值模拟的区域水量水质联合调度研究[J].水科学进展,2009,20(2):184-189. [2] 刘玒玒,汪 妮,解建仓,等.水库群供水优化调度的改进蚁群算法应用研究[J].水力发电学报,2015,34(2):31-36. [3] 张忠波,吴学春,张双虎,等.并行动态规划和改进遗传算法在水库调度中的应用[J].水力发电学报,2014,33(4):21-27. [4] 李 昱,彭 勇,初京刚,等. 复杂水库群共同供水任务分配问题研究[J].水利学报,2015,46(1):83-90. [5] 葛 忆, 顾圣平, 贺 军,等. 基于模拟与优化模式的流域水量水质联合调度研究[J]. 中国农村水利水电, 2013,(3):62-65. [6] 许碧娟,刘海军,孙 尚.一种遗传算法求解约束优化问题的新方法[J].辽宁工程技术大学学报,2006,25(11):141-143. [7] 林 丹,李敏强,寇纪凇.基于遗传算法求解约束优化问题的一种算法[J].软件学报,2001,12 (4):628-632. [8] 李敏强.遗传算法的基本理论与应用[M].北京:科学出版社,2002. [9] 周永华.实数编码遗传算法杂交算子组合研究[D].广州:华南理工大学,2003.3 实例应用与分析
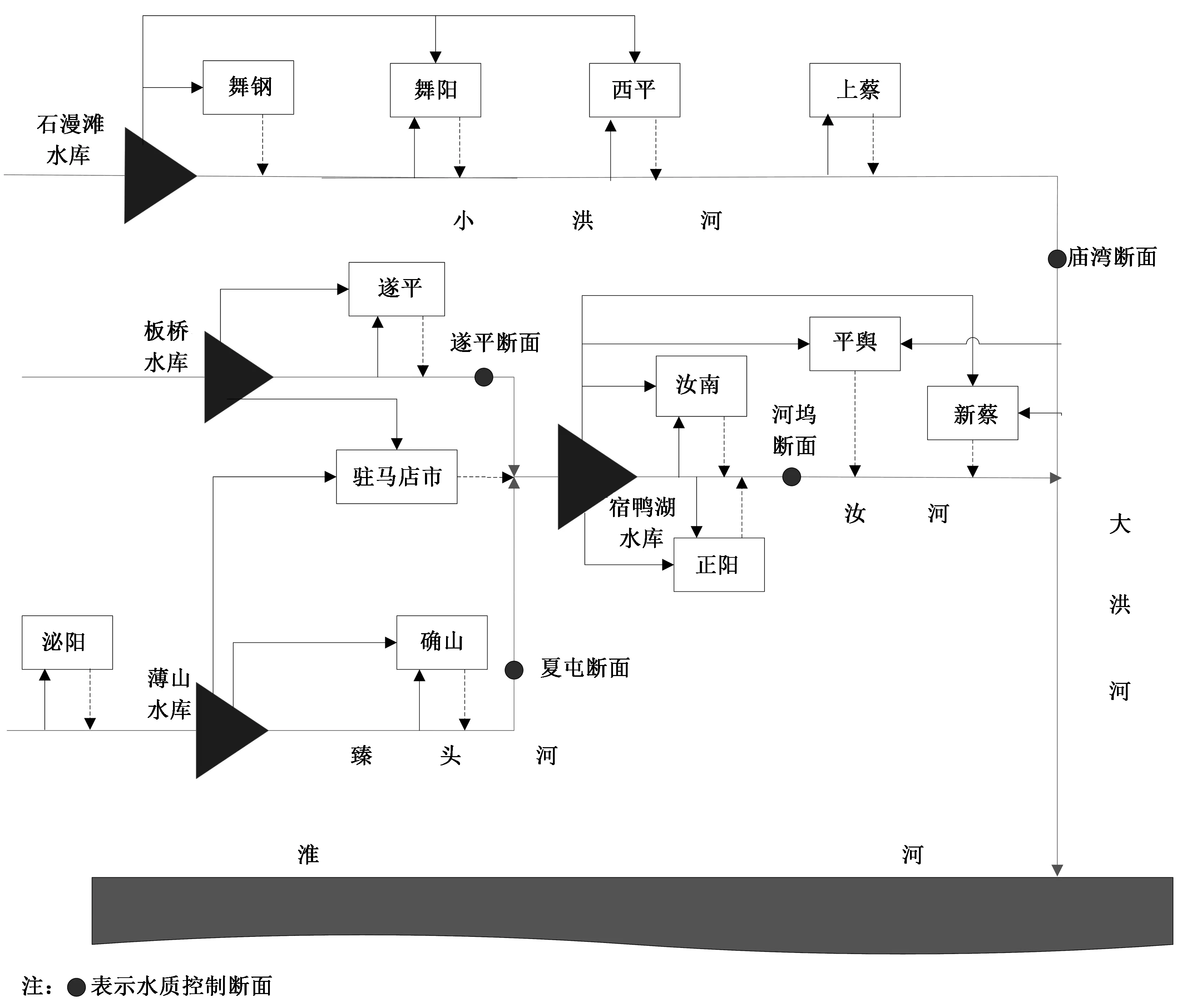
3.1 流域概况及分区概化

3.2 参数的分析与选取

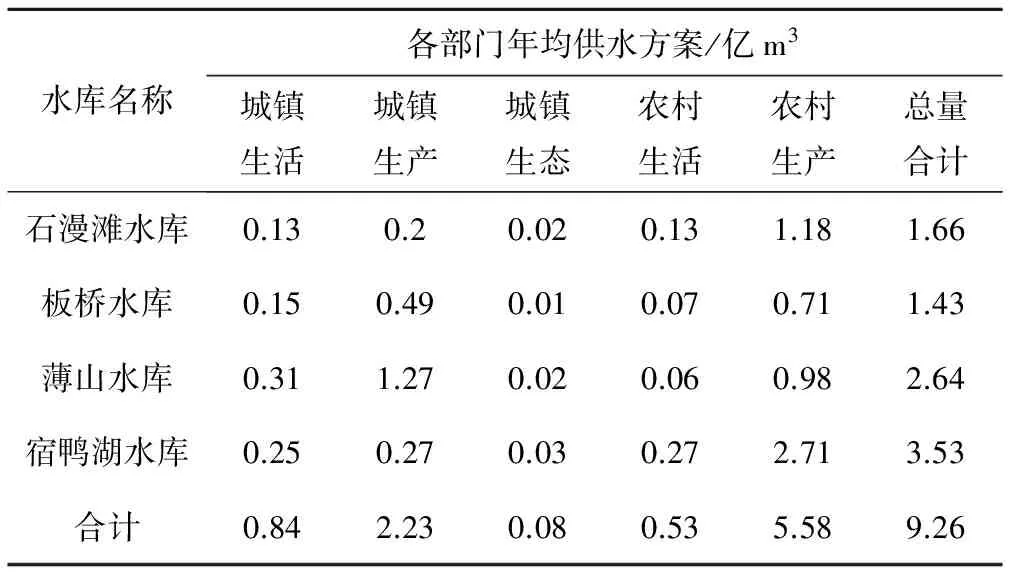
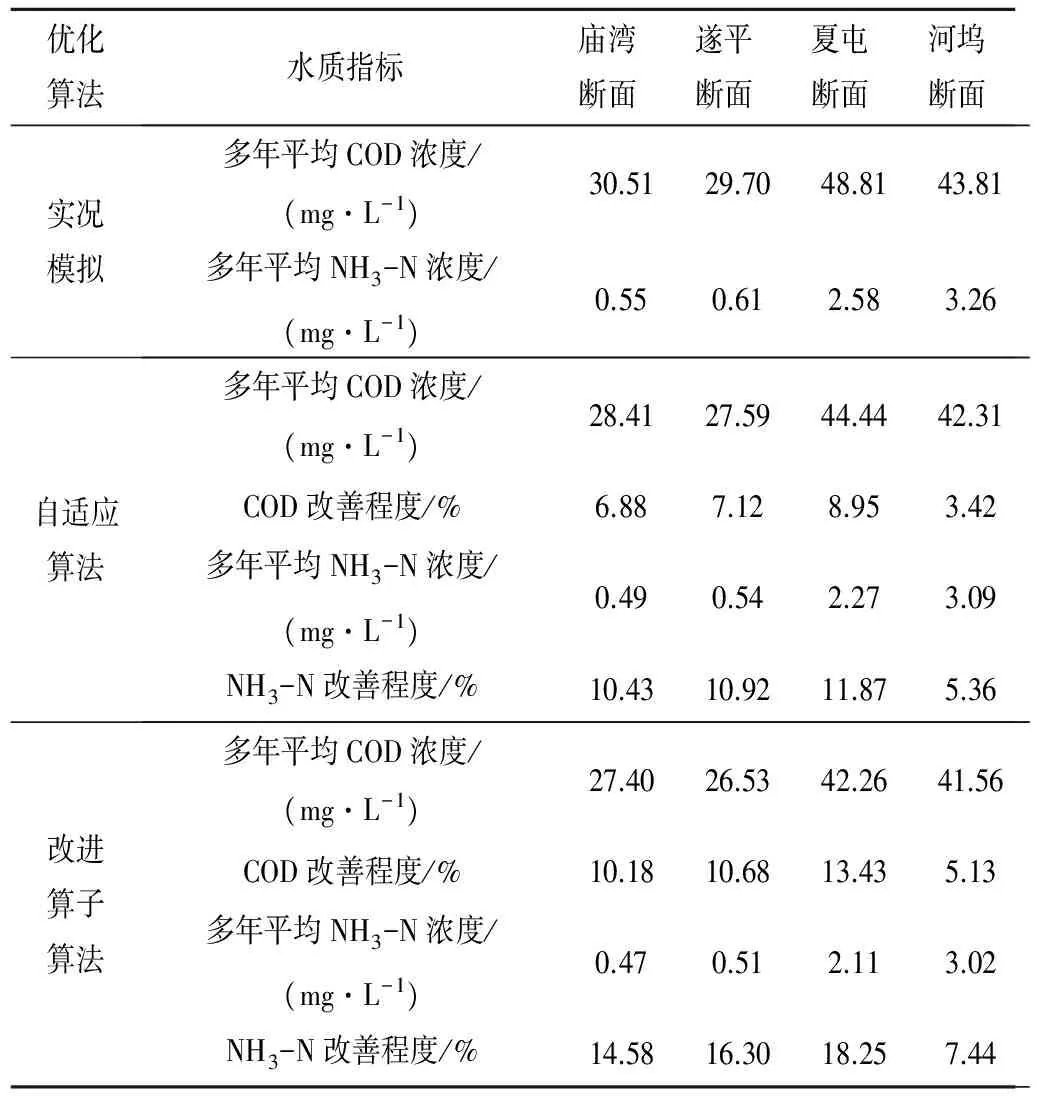
3.3 结果与分析


4 结 语

