有压泄洪洞中隔墩空化特性的试验研究

李 南，田 忠，范 强，王 韦，唐南波

(四川大学水力学及山区河流开发保护国家重点实验室，成都 610065)

0 引 言

高水头泄洪洞工作闸室的空化空蚀问题一直倍受关注。空化是水流在常温下因压强降低到某一临界值后，水体内部形成空穴、空洞或空腔的现象。国内外大量的工程实例说明，泄水建筑物中的一些部位，因设计或者施工问题，常常发生空化、空蚀的现象，如胡佛、格兰峡、二滩等工程的泄洪洞都曾经发生过空蚀破坏[1]。

一些工程由于布置、设计等需要，泄洪洞的单洞结构尺寸较大，因闸门的限制，需在闸室段加设中隔墩，闸室段被一分为二，从而减小了闸门尺寸，以便于高水头闸门的设计、制造和运行[2]，但闸室内流态相对复杂。目前，关于泄洪洞增设中隔墩后的水流特性研究大多针对水翅现象，纪伟和吴建华等[2,3]比较了不同体型的中隔墩在常压状态下的水翅现象并对产生机理进行了研究，提出了一种有效避免水翅危害的新体型。郭彬[4]提出了排洪涵洞中墩由半圆形变为圆弧形后水流冲击所受的阻力面面积减小，水翅跌入流道水面的流态有所改善。吴建华等[3]通过噪声测量系统测试了泄洪洞不同体型中隔墩尾部的初生空化数，进而判断中隔墩尾部的空化特性。鉴于此，作者在减压箱里开展了有压泄洪洞中隔墩的空化模型试验研究，分析了3种中隔墩体型的有压绕流空化特性，通过对比分析选出了较优体型。

1 试验设计与测试方法

1.1 模型设计

本文的研究结合某工程泄洪洞进行，工作闸室段前的压力洞洞径为12 m，之间由圆变方段过渡，工作闸室设置中隔墩，弧形闸门出口尺寸15 m×8.5 m(宽×高)，最大水头为120 m，最大泄量为3 317 m3/s，弧形闸门出口最大流速为39 m/s。

模型按重力相似准则设计，比尺为1∶40，模型全部采用有机玻璃制作，以方便观察过流时的水流流态，见图1。对于减压模型试验既须满足重力相似准则，又须满足空化相似准则，要求模型与原型的水流空化数相等，即：

(1)

式中：p/γ为水流相对压力；pa/γ为大气压力；pv/γ为水的饱和蒸汽压力；下标m指减压箱中的相关水力要素；下标p指原型的相关水力要素。

减压箱中应控制的真空压力为：

p0m/γ=pal/γ-pam/γ

(2)

式中：p0m/γ为相似条件下减压箱中应控制的真空压力；pal/γ为试验时减压箱所在地的大气压力；pam/γ为空化相似条件下减压箱中的大气压力。

相似真空度ηm可表示为：

(3)

相对真空度η/ηm可表示为：

(4)

式中：p0/γ为某一工况下减压箱中的实际真空压力，显然，当η/ηm=1时，为相似真空度工况；当η/ηm<1时，为低真空度工况。

图1 试验装置图(单位：m)Fig.1 Experimental setup

1.2 试验设备和测试仪器

本试验在减压箱里进行，减压箱箱体长20 m，宽1 m，高4 m。运行操作在中心控制室进行，可同时调节流量，检测水温，验室大气压等试验条件。噪声测量仪器采用丹麦B&K公司制造的8103型水听器(噪声频率测量范围0～100 kHz)、2635型电荷放大器、2636型测量放大器和成都泰斯特公司制造的TST5000动态信号分析系统。

1.3 测点布置和试验工况

由于中隔墩为左右对称结构，故在中隔墩头部上方和侧壁布置空化噪声测点1、2、3、4号，如图1、图2所示。从平面上看，中隔墩可看作由圆弧形的墩头和梯形的墩身组成，且头部的圆弧与侧壁的直线相切。为了分析泄洪洞中隔墩的空化现象，设计了3种体型的中隔墩，墩头形状分别为：尖形、椭圆形及半圆形，其中尖形由两段对称圆弧组成。中隔墩体型见图3，各墩头体型见表1。每个体型选取3个试验工况，即工况一：2 522 m3/s，工况二：3 141 m3/s，工况三：3 317 m3/s。

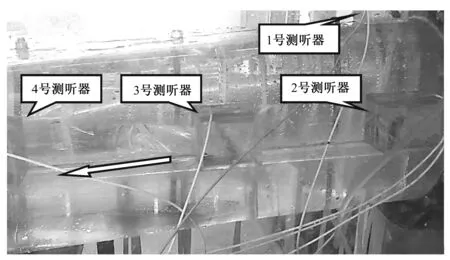
图2 水听器测点布置Fig.2 Layout sketch of the hydrophones

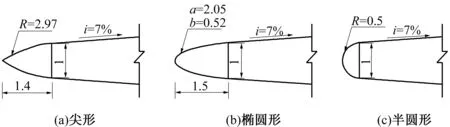
图3 中隔墩体型示意图(单位:m)Fig.3 sketch of middle-piers

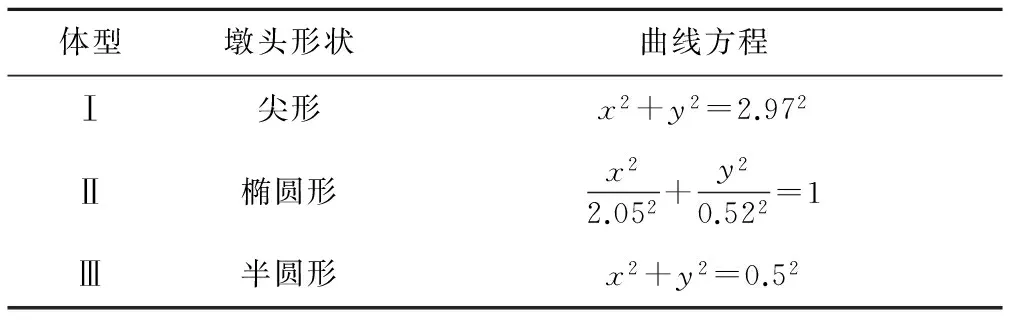
体型墩头形状曲线方程Ⅰ尖形x2+y2=2.972Ⅱ椭圆形x22.052+y20.522=1Ⅲ半圆形x2+y2=0.52

2 空化的判别标准

空泡的初生、发展和溃灭都会伴随着噪声，测量并分析空化噪声信号是一种研究空化的有效方法，减压试验对空化的判别一般采用目测法和噪声测试分析法相结合的方法，噪声测试分析法包括最大声压级差法和噪声能量比值法两种[5,6]。

目测法：当空化初生时，水流中出现的空化泡肉眼可见，当一分钟出现3～5个空化泡，被认为是空化初生[6]。

最大声压级差法：判断空化噪声声压级与背景噪声声压级差值得最大值是否大于临界值。声压级的计算公式为：

(5)

式中：SPL为声压级，dB；P所测得的声压，μPa；Pref为参考声压，μPa，试验中取Pref=1 μPa(MPa)。

声压级差值ΔSPL为所需相似真空度(η/ηm=1)下水流的噪声声压级与无空化发生时的背景噪声声压级之差，其中背景噪声的相对真空度η/ηm=80%。最大声级差为两条频谱曲线之间的最大差值。目前最大声压级差的临界值还没有统一的标准，文献[7,8]用5～10 dB作为空化初生的判别标准，文献[6]用10 dB作为空化初生的判别标准，文献[9]用17 dB作为空化初生的判别标准，文献[10]用10～20 dB作为空化初生的判别标准。

噪声能量比值法：判断噪声能量比值是否大于临界值。一般采用E/E0=2作为空化初生的判别标准[6]。水流噪声能量的计算公式为：

(6)

式中：ρC0为水的声阻抗；p(fi)为频谱声压级；Δfi为计算频带宽。

设背景噪声能量为E0，则不同相对真空度η/ηm的噪声能量比值为：

(7)

在试验中，最大声压级差的临界值取值为15 dB，噪声能量比值的临界值取值为2。

3 试验结果与分析

3.1 目测法

减压试验进行时，在箱体外观察中隔墩附近有无空化泡产生，统计空化泡个数，得出体型Ⅰ在工况三时平均1 min出现了1个空化泡；体型Ⅱ在工况三时没有看到肉眼可见的空化泡；体型Ⅲ在工况三时平均1 min出现了3个空化泡，空化强度较弱。

3.2 最大声压级差法

噪声频谱曲线采用100次采样曲线的历史平均值，分析区间取40～100 kHz。将所需相似真空度(η/ηm=1)，3个工况时4个水听器测点的最大噪声声压级差值列入表2。

从表2可以看出，3个体型的最大声压级差都小于15 dB，没有发生明显空化。3种中隔墩体型属于流线型，说明流线型中隔墩本身具有一定的抗空化能力。对于同一体型的同一部位，例如体型Ⅰ的1#测点，在工况一、工况二、工况三时的最大声压级差分别为5、9、12 dB，依次递增，其他体型、测点规律大致相同，说明同一个体型水流流速越大，越容易空化；下面就以最危险的工况三来分析，对于同一体型的不同部位，例如体型Ⅰ的4个测点，最大声压压级差分别为12、5、5、7 dB，先减小再增大，其他两个体型规律类似，说明在有压泄洪洞里，中隔墩头部发生分流现象，容易发生空化，依次为尾部，中部；对于不同体型的同一部位，例如三个体型的1号测点，最大声压级差分别为12、10、14 dB，其他3个测点规律类似，说明半圆形墩头容易空化，依次为尖形、椭圆形。

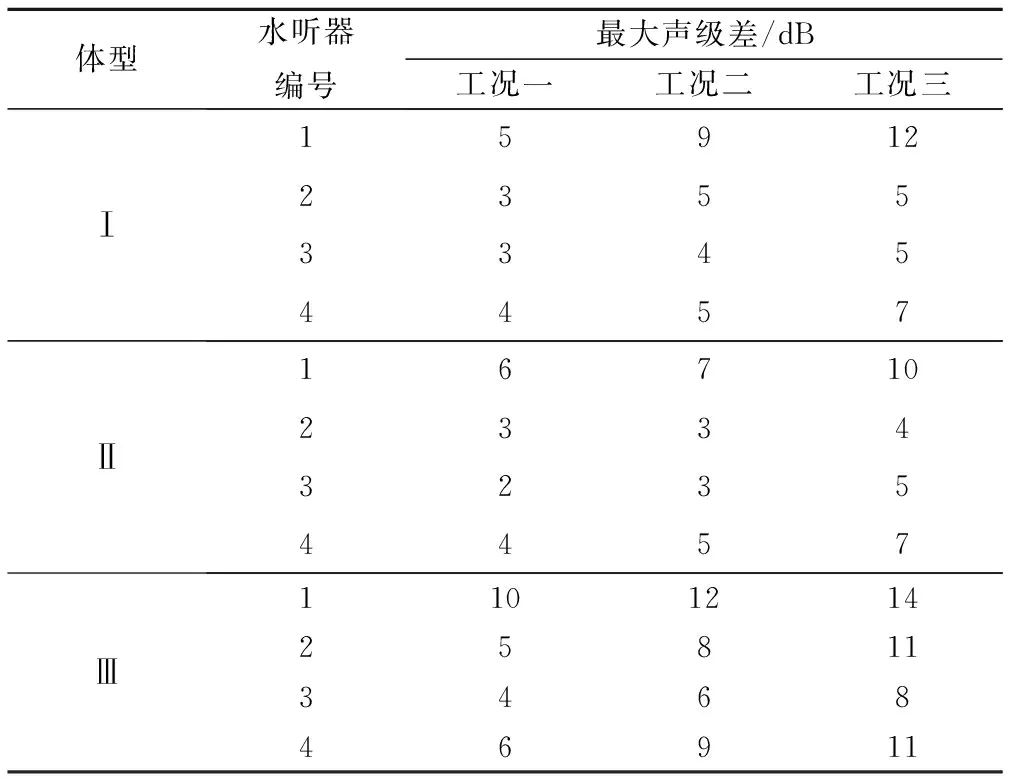
表2 相似真空度下最大声压级差值表Tab.2 Maximum SPL differences at similarity vacuum pressure

由上述分析知，中隔墩头部，即1#测点附近最容易空化，这里列出了体型Ⅰ、Ⅱ、Ⅲ、的1号测点空化噪声的频谱曲线图，见图4～图6，其他测点规律类似。

图4 体型Ⅰ空化噪声频谱曲线Fig.4 Spectrum curve of noise of the middle-pier with shapeⅠ

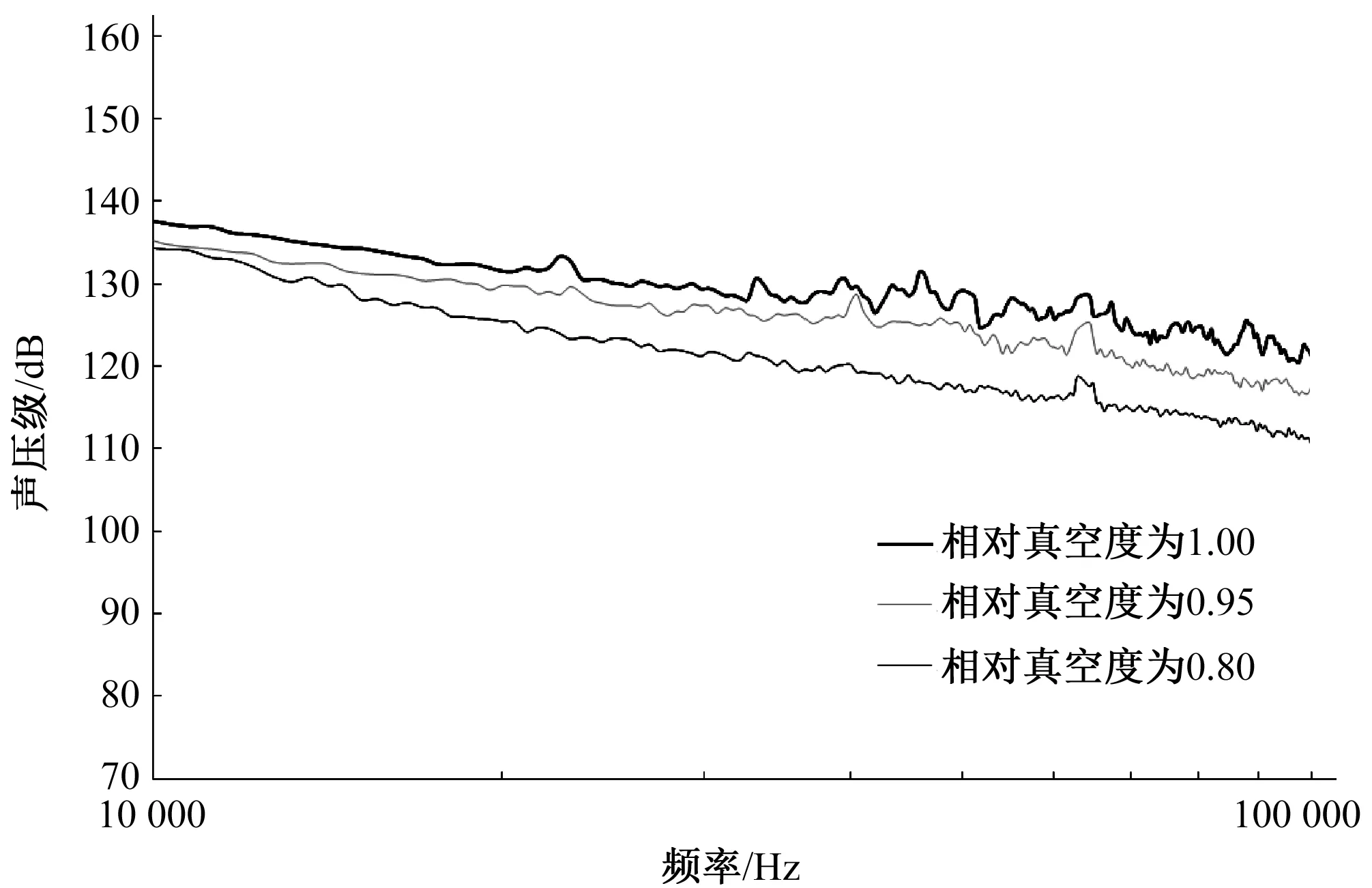
图5 体型Ⅱ空化噪声频谱曲线Fig.5 Spectrum curve of noise of the middle-pier with shapeⅡ

图6 体型Ⅲ空化噪声频谱曲线Fig.6 Spectrum curve of noise of the middle-pier with shape Ⅲ

3.3 能量比值法

由上面最大声压级差法分析可知，中隔墩头部(1号测点附近)较易发生空化，此处以1号测点为例分析，将不同体型在工况三时的噪声能量与背景噪声能量的比值和相对真空度的关系绘入图7。从图7中可以看出，3个体型的相似真空度噪声能量比值都小于2，体型Ⅲ的曲线位于最上方，体型Ⅱ的曲线位于最下方，同样也说明了3种中隔墩体型都没有发生空化，且椭圆形墩头最优，半圆形墩头最差。

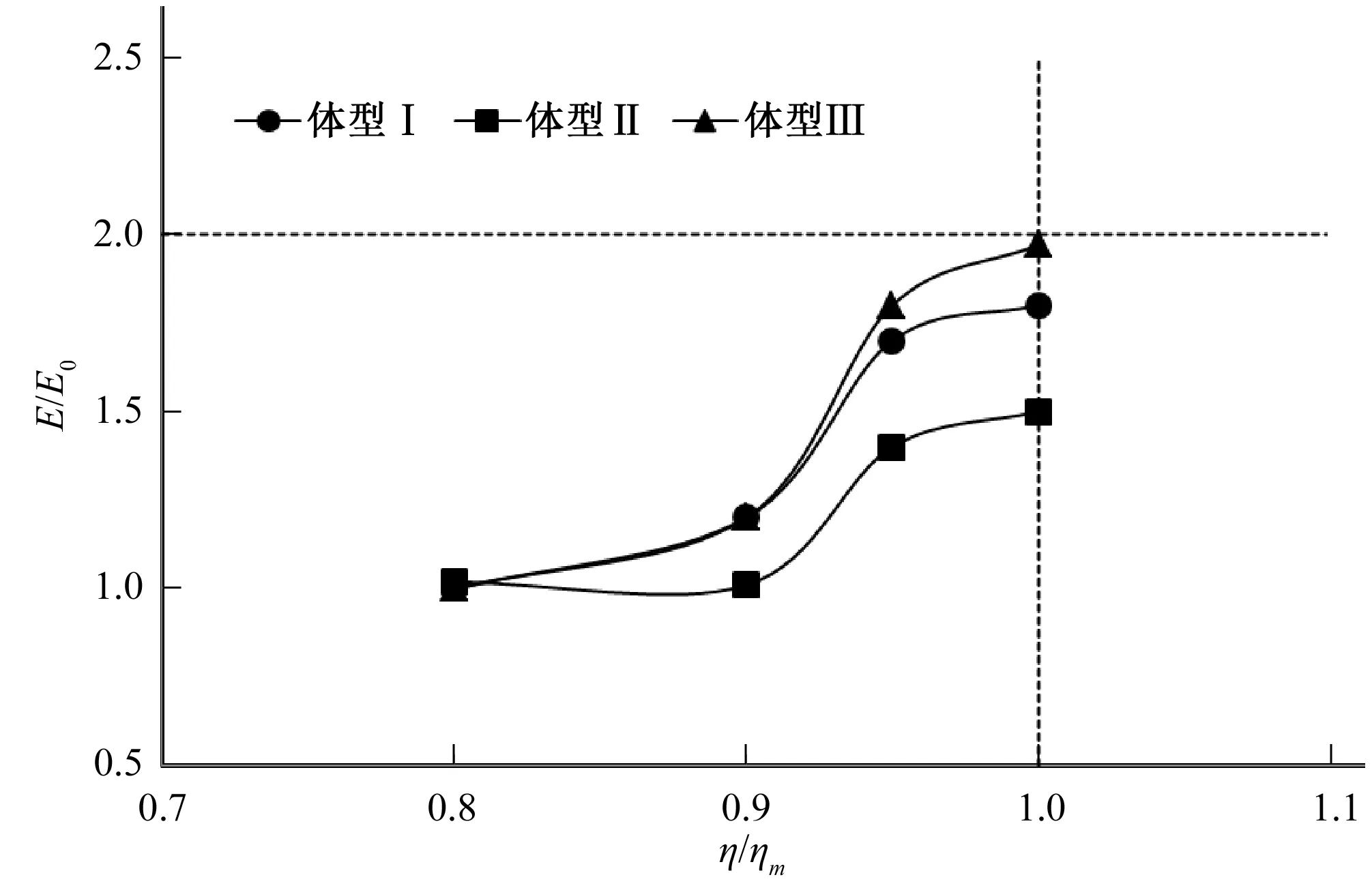
图7 1号测点不同η/ηm条件下的噪声能量比值曲线Fig.7 Noise energy ratio (E/E0) of 1# hydrophone versus η/ηm with different head shapes

4 结 论

本文针对高水头大流量泄洪洞增设中隔墩后的空化问题进行了减压模型试验，测量了3种不同体型中隔墩的空化噪声，采用目测法、最大声压级差法、能量比值法对空化特性进行了综合分析，结果表明。

(1)在有压泄洪洞里，3种中隔墩体型属于流线型，都没有发生明显空化，但体型Ⅲ(半圆形墩头)可能已发生弱空化，说明流线型中隔墩本身具有一定的抗空化能力。

(2)水流在中隔墩头部发生分流现象，此处较容易发生空化，其次为尾部、中部。

(3)通过对3种体型的对比分析得，椭圆形墩头最优，依次为尖形，半圆形。本文提出的中隔墩体型可供类似工程参考。

□

[1] 郭 军，张 东，刘之平，等.大型泄洪洞高速水流的研究进展及风险分析[J].水利学报，2006，37(10)：1 193-1 198.

[2] 纪 伟，吴建华，阮仕平.泄洪洞中墩水翅现象的试验研究[J].河海大学学报(自然科学版)，2007，35(1)：18-21.

[3] WU Jian-hua, CAI Chang-guang, JI Wei. Experimental study on cavitation and water-wing for middle-piers of discharge tunnels[J]. Journal of Hydrodynamics, Ser. B., 2005,17(4):429-437.

[4] 郭 彬.排洪涵洞中墩水翅现象试验及数值模拟研究[D].南京：河海大学，2008.

[5] 严根华，陈发展，郭熙宏，等.向家坝水电站底孔封堵门槽与工作门槽抗空化试验研究[J].水力发电学报，2010，29(2)：47-54.

[6] 许文海，李国栋，卢泰山，等.泄洪洞突扩突跌段空化特性的试验研究[J].西安理工大学学报，2007，23(1)：20-24.

[7] 余 挺，田 忠，王 韦，等.收缩式洞塞泄洪洞的消能和空化特性[J].水利学报，2011，42(2)：211-217.

[8] 姜伯乐，张 晖，杨江宁.三峡电站排沙孔工作门区及通气管道空化特性研究[J].长江科学院院报，2013，30(8)：46-49.

[9] 薛 阳，刘韩生，安梦雄.积石峡水电站中孔泄洪洞平板工作闸门槽空化特性研究[J].水力发电学报，2009，28(3)：152-156.

[10] 周宪政.用声学原理测空化噪声的有关方法探讨[C]∥水科学青年学术论文集.北京：水利电力出版社，1990.