农灌区地下水开采对径流的影响模拟研究

宋琪峰， 陈 喜， 黄日超， 张志才

(1 河海大学水文水资源与水利工程科学国家重点实验室， 南京 210098; 2 河海大学水文水资源学院，南京 210098)

在人类活动强烈的平原地区，由于地下水过量开采，地下水位的大幅度下降，引发河道断流、土壤沙化等生态环境问题。在华北平原地区，地下水开采量从20世纪70年代的156.57亿m3/a,增加到211.98亿m3/a。山前平原区浅层地下水位普遍下降10～30 m,中东部平原下降5～10 m,滨海平原下降0～5 m。“华北平原环渤海复合大漏斗”覆盖了河北、北京、天津及山东的广大平原,占区域的52%[1]。淮河流域平原区20 世纪80 年代后期开采量剧增,地下水位也呈逐年下降趋势，淮北地区已形成6 961 km2地下水降落漏斗[2]。地下水位的大幅度下降，使得包气带加厚且变得干燥，最终出现径流系数下降、降雨径流关系发生变化[3]，地下水补给及赋存环境发生了变化，因此，分析地下水开采对区域水文循环影响，成为变化环境下水文循环规律及水资源转化关系研究的重要内容[4]。

农灌区水文过程涉及降水-土壤水-地表水-地下水“四水”转化以及考虑植物耗水的“五水”转化，水文模型是研究“四水”、“五水”转化定量模拟的重要手段。近年来，以地下水开采为主的农灌区从关注地下水位动态及其补排关系数值模拟，发展到地表水与地下水耦合模拟，如SWAT与MODFLOW耦合[5]、PRMS与MODFLOW耦合[6]。近年来发展到考虑人为过程水的输送，如贾仰文等构建的模拟水分在地表、土壤、地下、河道以及人工水循环系统中运动过程的“二元”分布式水文模型[7]，这些模型适用于不同研究对象和资料条件。由于开采机井分布面广量大，地下水开采量统计资料时空分布精度难以满足分布式模型要求。因此，考虑平原区水循环和水资源利用特点，改进和发展概念性水文模型，也是平原灌区水文过程模拟的重要手段，如胡和平等针对干旱区平原绿洲水土资源利用特点,建立了以农区土壤水为中心的平原绿洲散耗型水文模型，重点考虑人类活动如引水灌溉、地下水的开采等对水平衡的影响[8]。

传统概念概念性水文模型-新安江模型能较好地模拟流域产汇流过程，但该模型无法计算含水层地下水动态。本文在该模型基础上加入地下水蓄水库演算过程，以河川径流和地下水位作为目标函数，率定模型参数，分析地下水位动态变化及其对河川径流影响。

1 模型基本原理

1.1 产流计算及水源划分

非饱和带水量平衡式为：

Wt+1=Wt+PEt+Egt

(1)

式中：Wt、Wt+1分为t和t+1时刻流域平均蓄水量；Egt为潜水蒸发量；PEt为净雨量：

PEt=Pt+Wgt-Et

(2)

式中：Pt为时段降雨量；Wgt为时段灌溉开采量。灌溉水量不产流，但部分回归补给地下水；Et为蒸发量，采用新安江模型三层蒸发模式计算，各量均以深度表示。

基于新安江模型蓄满产流计算模式，采用指数型蓄水容量曲线，根据净雨量PEt计算产流量 。在平原农耕区，耕犁层以上渗透性大，耕犁层渗透性小，降雨时耕犁层易形成自由水。因此，将自由水概化为两个水库，即耕犁层上部自由水库和下部地下水蓄水库(潜水含水层饱和地下水)。上部自由水库进一步划分地表径流、壤中流，地下水蓄水库出流为河川基流，其蓄量受降雨入渗补给、地下水开采影响，模型结构如图1所示。

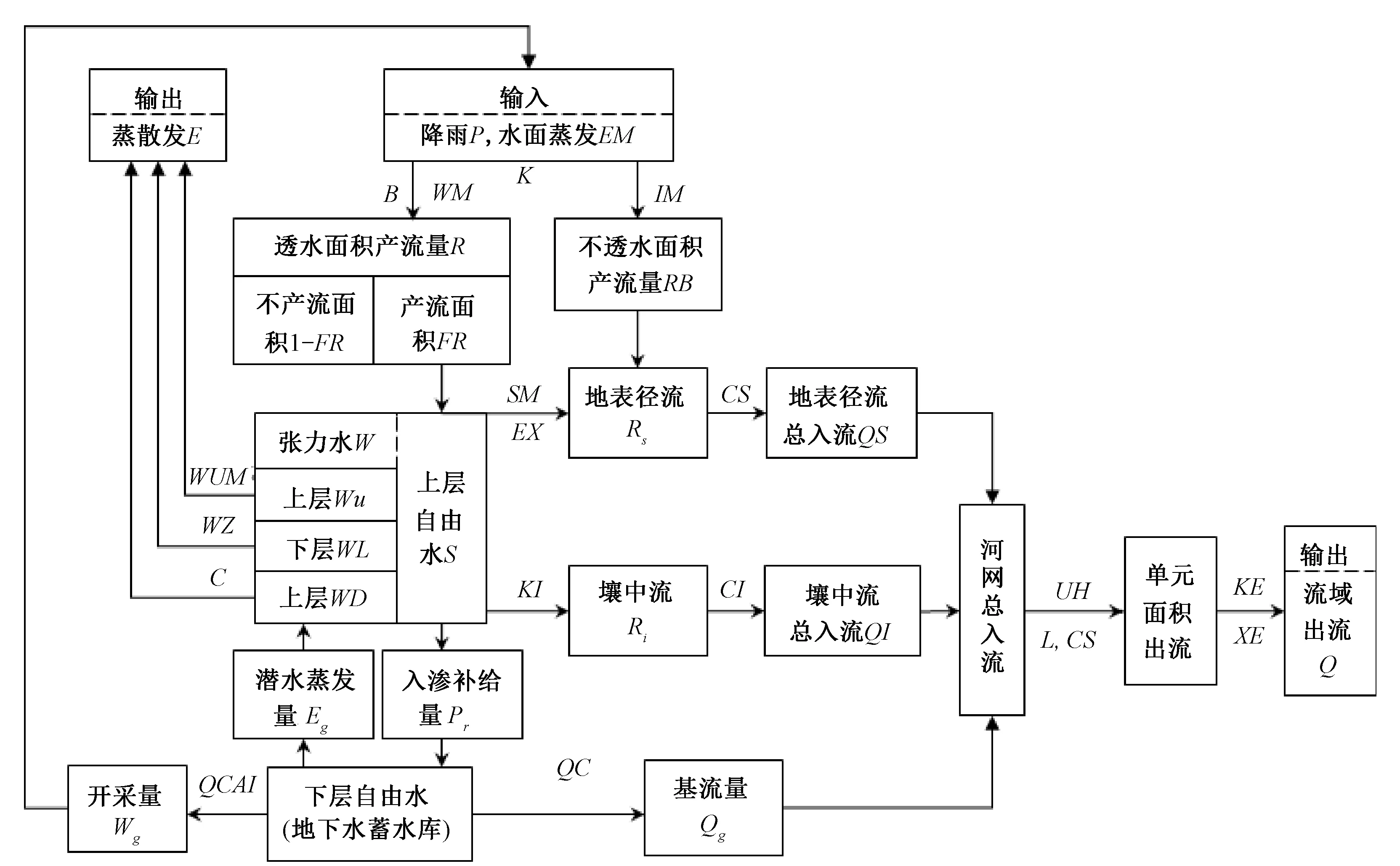
图1 模型结构图

1.2 潜水含水层水平衡及补排项计算

潜水含水层概化为地下水蓄水库，其水量平衡公式为：

Sgt+1=Sgt-Egt+Prt-Wgt-Qgt

(3)

式中：Sgt、Sgt+1分别为t、t+1时刻地下水库蓄水量；Prt为入渗补给量；Wgt为开采量；Qgt为地下水蓄水库出流量(基流量)。

各项计算方法如下：

(1)入渗补给量。降雨入渗补给量与土壤蓄水量成正比。若P+Wg-E<0，则某一面积(f/F)内补给量为：

作者在这一部分提出，无论是再现式、表现式还是印象式翻译，都具有自己的局限，都会对诗歌翻译形成干扰，唯有将这三种艺术方式进行调和性实施，才能最大限度地保证译诗的艺术性。有鉴于此，作者提出了诗歌翻译体现论，并认为其中所包含的心身化结构和物身化结构都可以用此三种观念进行解说。作者参照中西方绘画艺术观念，将翻译分为“观译”和“看译”两种路径，并提出“观译”是更为理想的翻译方式。该书以“感”为核心概念，串联起诗歌翻译的不同环节，描述了翻译不同阶段触发的感应活动，以及作者、译者、译诗读者之间可能产生的感应交流。

(4)

式中：a为考虑土湿影响的入渗补给系数；WMM为流域平均最大蓄水容量。

考虑流域蓄水量非均匀性，采用流域蓄水容量曲线，在流域面上积分得到流域平均入渗补给量：

(5)

(6)

式中：f/F为蓄量W所占流域面积比例， 为单点最大蓄水量；WM为流域平均蓄水容量；b为蓄水容量曲线指数，WMM=WM×(1+b)/(1-IM)。

若P+Wg-E<0，Prt=0

(7)

(2)潜水蒸发量

Eg=η×EP×(1-D/Dmax)n

(8)

式中：η为蒸发折算系数；EP为蒸发皿蒸发量；D、Dmax分别为地下水埋深和极限埋深；n为系数。

(3)地下水开采量。由于研究区地下水开采量Wg主要用于农业灌溉，根据气象条件和农作物类型计算的农业灌溉需水量WI进行估算：

Wg=βWI

(9)

式中：β为开采折算系数。

Qg=kgSg

(10)

式中：kg为地下水出流系数；SG为地下水库蓄量。

计算公式为：

Sg=Sy(Dz-D)

(11)

式中：Sy为给水度；Dz为基流接近于0的埋深，根据枯季径流与地下水埋深关系，Dz的取值范围2～4 m之间。

(5)考虑地下水埋深空间分布的潜水蒸发和补给量计算。研究区不同地点地下水埋深存在差异，进而影响上述潜水水平衡项，地下水埋深空间分布假设为Gamma分布[9-15]：

(12)

式中：Γ(γ)为Gamma函数；α为形状参数；γ为尺度参数。

根据Gamma分布参数之间关系，γ=α/E(d)，E[d]为地下水埋深空间分布均值。由此，流域平均潜水蒸发量Eg、出流量Qg为：

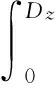
(13)

(14)

流域产流量R扣除进入地下水蓄水库(即入渗补给量Pr)水量，按自由蓄水库曲线划分为地表径流Rs和壤中流Ri，经过线性水库调蓄进入河道。地下径流按式(13)排泄至河道，河道汇流采用马斯京根方法计算。

2 应用实例

2.1 流域概况及资料

选取淮河流域临涣集子流域作为研究对象，流域面积2 560 km2，流域内有16个雨量站，2个蒸发站，1个水文站和44个地下水观测站点(图2)。采用泰森多边形计算流域面平均降雨量、地下水位埋深。多年平均降雨量为673.93 mm，多年平均蒸发皿蒸发能力997.73 mm，多年平均流量4.78 m3/s。

采用1990-1995年实测逐日降水、蒸发皿蒸发量、流量以及5日地下水位进行模型参数率定，采用1986-1989年资料进行模型验证。

图2 临涣集流域雨量，蒸发，水文和地下水位站点

2.2 模型模拟结果及参数灵敏性分析

采用河川流量模拟的纳什效率系数(NSC)、均方误差(RMSE)以及地下水埋深模拟确定性系数R2和NSC进行模型参数率定与模型验证，结果见表1和图3、4。结果表明，模型能较好地模拟研究区径流及地下水动态变化，具有较好的适用性。

表1 模型模拟与实测统计结果

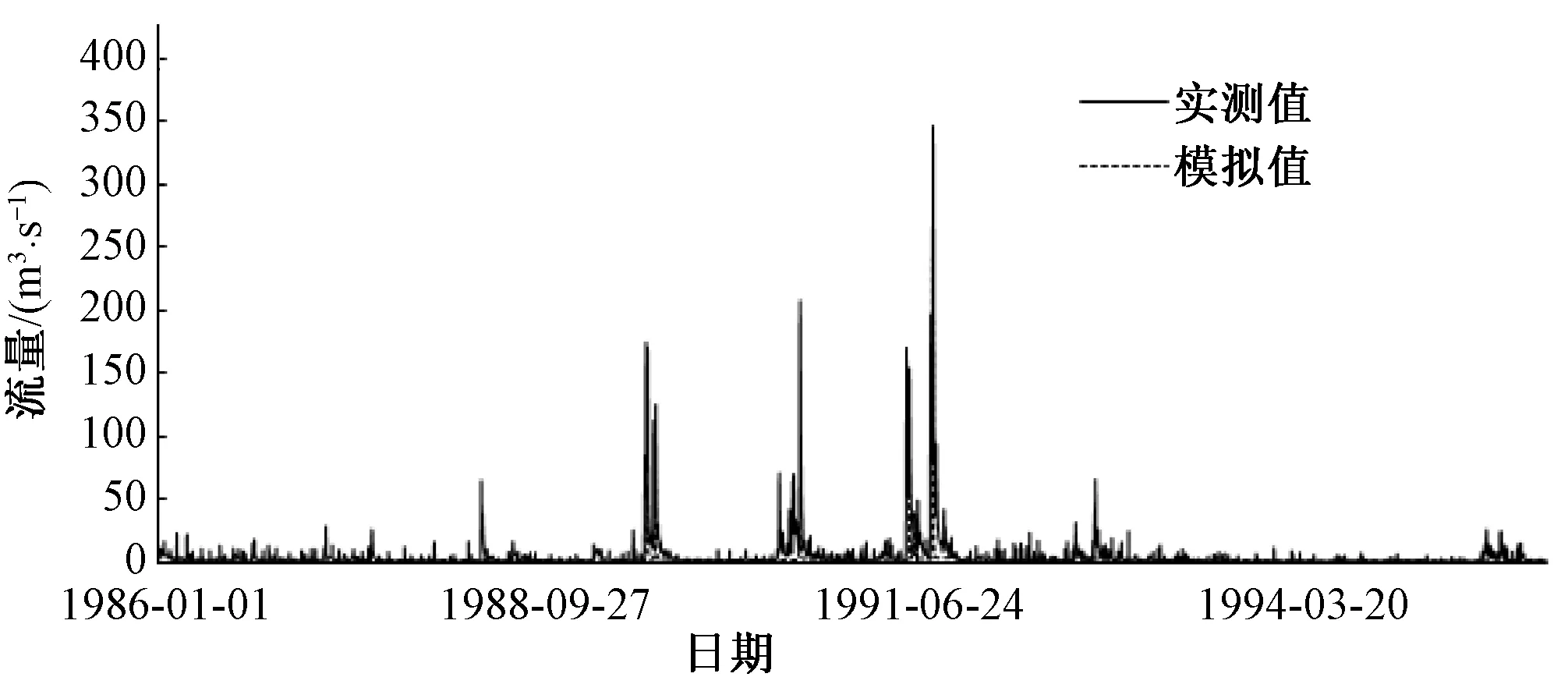
图3 模型模拟与实测日径流

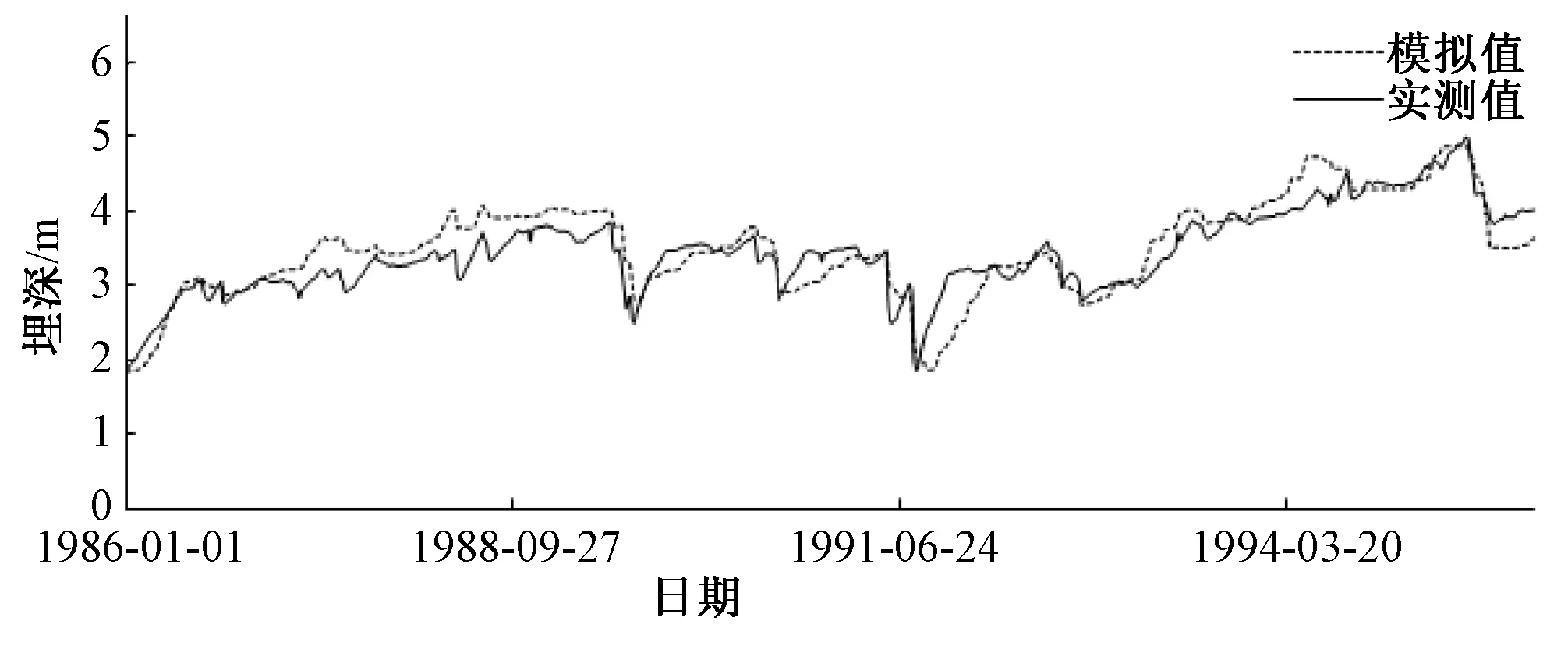
图4 模型模拟与实测地下水埋深

以日径流和地下水埋深的NSC为目标函数，当参数变化10%时，日径流和地下水埋深NSC的变化如图5所示。结果显示，对日径流比较敏感的参数为η、ac、WMM；对地下水埋深比较敏感的参数为η、a、kg、b、β、WMM、n、WUM。

图5 参数敏感性分析

2.3 地下水开采对河川径流量影响分析

设定不同开采强度情景，利用模型模拟不同开采强度对多年平均径流量以及不同量级径流量的影响(表2、图6)。结果表明，当开采量增加一倍，多年平均流量减少23.6%。地下水开采对大的雨洪流量影响很小，如当流量大于10 m3/s时，开采量变化对流量频率影响较小，开采量增加50%和100%，流量分别减小1.9%和3.2%；随着流量减小，地下水开采对流量影响越趋显著。当流量在0～10 m3/s范围，当开采量增加，日流量频率有明显的减小趋势，开采量增加50%和100%时，流量分别减小20.2%和35.0%。因此，开采量增加，将导致枯季径流量减少显著(图6)。

表2 开采量增加引起的流量变化

图6 开采增加对日流量频率的影响

3 结 语

本文利用改进的新安江模型，通过模拟计算，分析了农灌区地下水开采对径流的影响，得到以下主要结论：

(1)改进了新安江模型，建立考虑地下水埋深统计分布特征的降水入渗补给量、潜水蒸发量计算方法以及河川径流量与地下水埋深的计算方法。

(2)利用临涣集流域实测气象、水文资料，对模型进行了参数率定及模型验证，通过灵敏性分析，蒸发折算系数、入渗补给系数、流域平均最大蓄水容量及对日径流与地下水埋深较为敏感。

(3)通过对研究区不同开采情景下径流与地下水位的动态模拟，对比分析了农灌区地下水开采对径流及地下水的影响，开采量增加导致枯季径流量减少显著，当流量在0～10 m3/s范围，开采量增加50%和100%时，流量分别减小20.2%和35.0%。

□

[1] 夏 军. 华北地区水循环与水资源安全：问题与挑战[C]∥ 第八届海峡两岸水利科技交流研讨会，2004.

[2] 姬 宏,王振龙,李 瑞. 淮北平原区地下水资源演变情形研究[J]. 水文，2009,29(1):59-62．

[3] 陈敏建. 水循环生态效应与区域生态需水类型[J]. 水利学报，2007,38(3):282-288．

[4] Logan W., Groundwater fluxes across interfaces[M]. The National Academy of Science, USA, 2004.

[5] 刘路广，崔远来. 灌区地表水-地下水耦合模型的构建[J]. 水利学报，2012，(7):826-833.

[6] Woolfenden, L.R., and Nishikawa, Tracy, eds., 2014, Simulation of groundwater and surface-water resources of the Santa Rosa Plain watershed, Sonoma County, California: U.S. Geological Survey Scientific Investigations Report 2014-5052, 258 p., http:∥dx.doi.org/10.3133/sir20145052.

[7] 贾仰文，王 浩，周祖昊，等. 海河流域二元水循环模型开发及其应用 -1模型开发与验证[J]. 水科学进展，2010，21(1)：1-8.

[8] 胡和平,汤秋鸿,雷志栋,等，干旱区平原绿洲散耗型水文模型-Ⅰ模型结构[J]. 水科学进展，2004，15(2)：140-145.

[9] Beldring S, Gottschalk L, Seibert J, et al. Distribution of soil moisture and groundwater levels at patch and catchment scales[J]. Agricultural and Forest Meteorology, 1999,98-99:305-324.

[10] Yeh P J, Eltahir E A B. Representation of Water Table Dynamics in a Land Surface Scheme. Part Ⅱ: Subgrid Variability[J]. Journal of Climate, 2005,18(12):1 881-1 901.

[11] Lo M H, Famiglietti J S, Yeh P F, et al. Improving parameter estimation and water table depth simulation in a land surface model using GRACE water storage and estimated base flow data[J]. Water Resources Research, 2010,46(5).

[12] Koirala S, Yeh P, Oki T, et al. Fully Dynamic Groundwater Representation in the MATSIRO Land Surface Model[J]. Annual Journal of Hydraulic Engineering, Japan Society of Civil Engineers, 2010,54:37-42.

[13] KOIRALA S, YAMADA H G, Yeh P J, et al. Global simulation of groundwater recharge, water table depth, and low flow using a land surface model with groundwater representation[J]. Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering), 2012,68(4):211-216.

[14] Takata K, Emori S, Watanabe T. Development of the minimal advanced treatments of surface interaction and runoff[J]. Global and Planetary Change, 2003,38(1):209-222.

[15] Beven K J, Kirkby M J. A physically based, variable contributing area model of basin hydrology[J]. Hydrological Sciences Bulletin des Sciences Hydrologiques, 1979,24(1):43-69.