一种无资料地区山洪灾害临界雨量计算方法研究

姬 晶，刘 攀，江炎生，刘德地，邓 超，李泽君，桂梓玲，赵 燕，潘正可，张晓琦

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 水资源安全保障湖北省协同创新中心，武汉 430072；3. 湖北省防汛抗旱指挥部办公室，武汉 430071)

0 引 言

山洪是指丘区溪沟中由强降水诱发生成的暴涨洪水，山洪灾害严重威胁生命财产安全，占全国洪涝灾害死亡人数的80%以上。山洪由于资料短缺以及具有流速快、预见期短等特点，因此山洪灾害主要侧重在对山洪预警方面的研究[1]。山洪预警技术一般主要是在对雨量、洪水资料进行统计分析，确定出临界雨量。临界雨量是指导致一个流域或区域发生山溪洪水可能致灾时，降雨达到或超过的量级和强度[2]，降雨、土壤含水量以及下垫面是临界雨量分析的关键因素。可采用统计归纳法[3]、经验估计法[4]、降雨分析法[5]、水文水力学法[6]以及模型分析法[7]等方法进行临界雨量的分析。而当采用模型分析法时，一般由于山洪发生区缺乏实测的降水径流资料，水文模型参数不能直接率定，从而导致临界雨量难以确定。由暴雨等值线图确定出的设计暴雨与设计洪水在工程实践中已广泛应用，而在无资料地区的设计洪水推求中，由设计暴雨产汇流形成设计洪水，隐含了前期影响雨量较湿的假定，可作为特例估计模型参数。本文以设计暴雨与相应的设计洪水为基础，采用二水源新安江模型和SCS模型，以湖北省宜昌市点军区为研究实例，开展山洪灾害的临界雨量推求研究。

1 临界雨量推求

基于二水源新安江模型和SCS模型，进行临界雨量的推求，具体流程如图1所示，步骤如下：

(1)首先假定一个初始雨量，在各小流域的汇流时间对应的雨量频率曲线上内插出该假设雨量对应的频率；

(2)根据各时段的典型雨量时程分配计算出该频率下的暴雨过程；

(3)将该暴雨过程作为水文模型(选用二水源新安江模型和SCS模型)的输入，即可求得各小流域控制断面处的洪水过程，从洪水过程中挑选出洪峰流量并将其与调查的控制断面处的成灾流量进行对比，如若不一致，则重新进行雨量的假定，直到试算出该断面处的洪峰流量与成灾流量的误差在可接受范围内(ε=0.03)，则此时假定的雨量即为临界雨量。

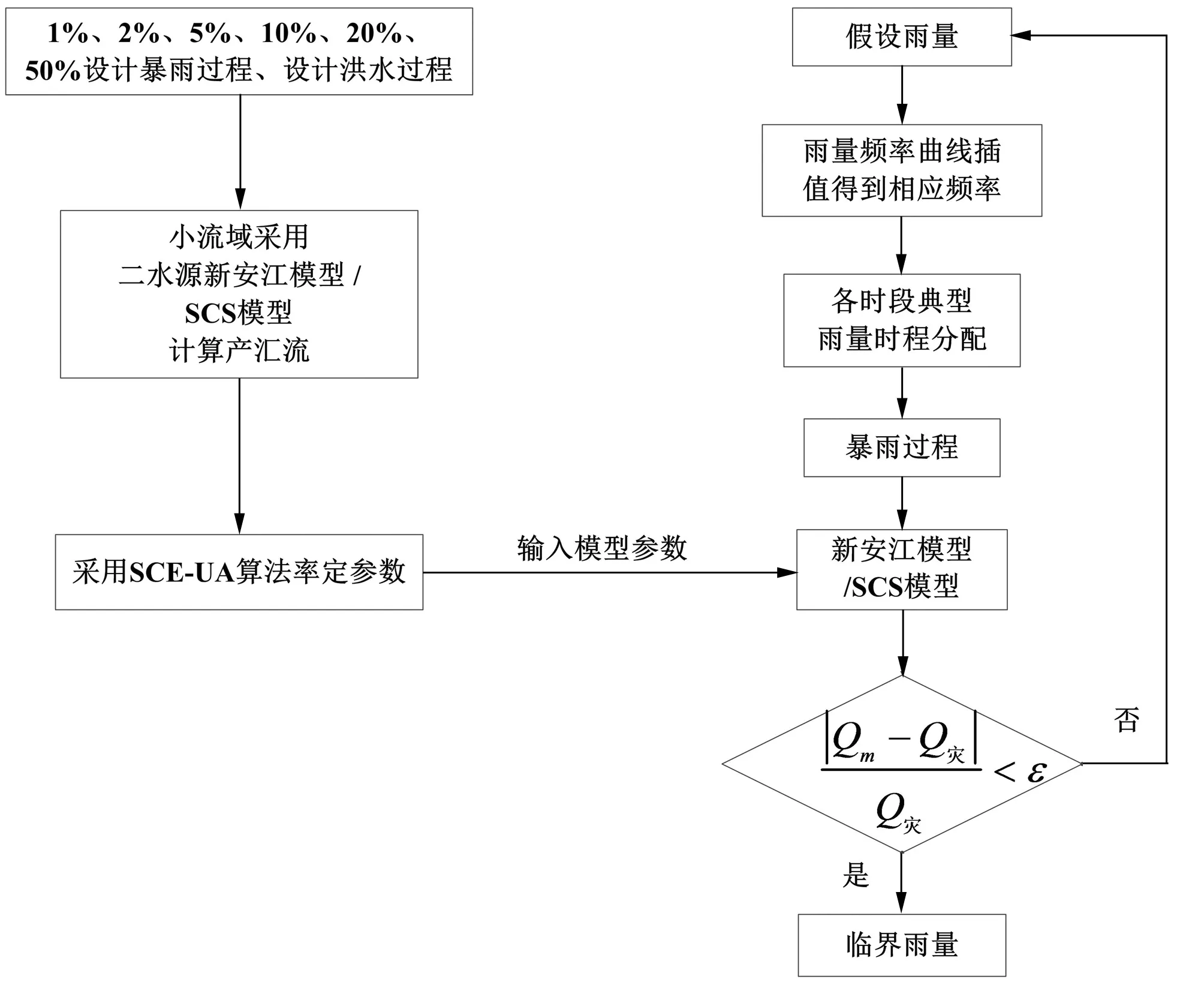
图1 临界雨量计算流程图Fig.1 The flow chart for the calculation of critical precipitation

1.1 二水源新安江模型

如图2所示，二水源新安江模型采用蓄满产流假定进行产流计算，将流域内各点不同土壤含水容量概化成蓄水容量曲线。二水源新安江模型将净雨划分成地面径流和地下径流，其中地面径流采用单位线进行汇流计算，地下径流经过线性水库的调蓄作为地下水出流，地面径流与地下径流之和形成出口断面流量过程。

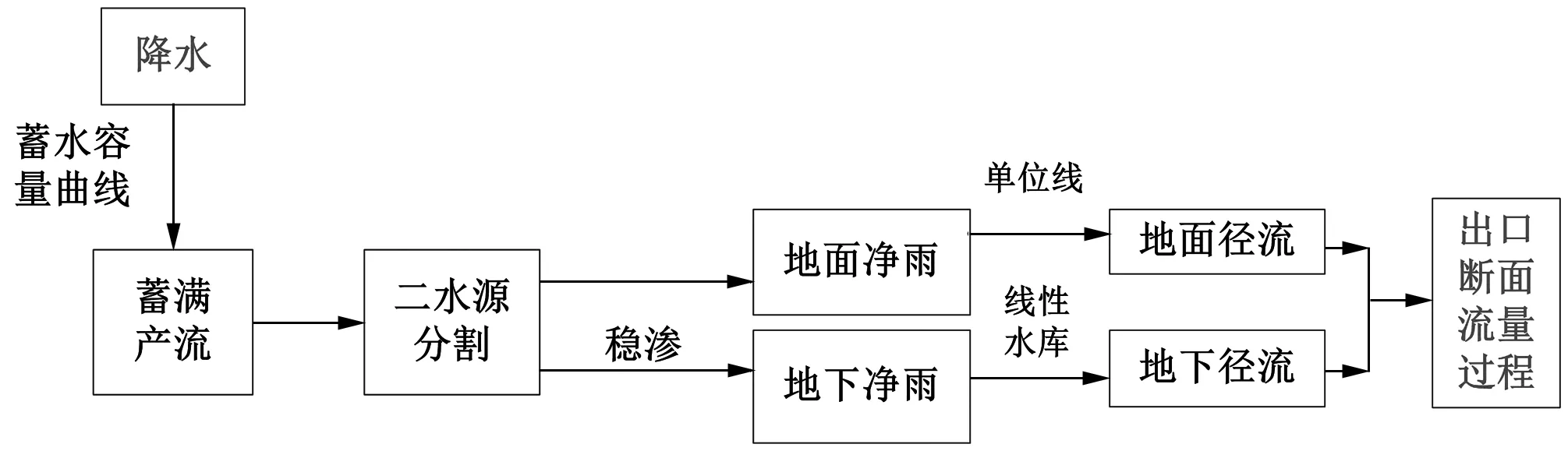
图2 二水源新安江模型计算流程图Fig.2 The flow chart of Xin'anjiang model

1.2 SCS模型

SCS模型是美国农业部水土保持局于1954年开发流域水文模型[8]，被广泛应用于美国及世界其他各国。SCS模型的建立基于水平衡方程以及两个基本假设，即比例相等假设和初损值-当时可能最大潜在滞留量关系假设[9]。Mishra和Singh在总结SCS模型的基础上提出了改进的通用SCS模型[10]。模型地面径流计算如下：

(1)

式中：i为计算时段；P为降雨总量，mm；Ia为初损，mm，主要指截流、表层蓄水等；Fc为下渗静态部分，mm；W为土壤含水量，mm；S为可能最大滞留量，mm。

Mishra和Singh将累积下渗F分为下渗静态部分Fc和动态部分Fd[10]。式(1)在Pi+1≥Ia,i+Fc,i+1时成立，否则ROi+1=0。若Pi+1≤Ia,i，则Fc,i+1=0且ROi+1=0。若Pi+1≤Ia,i+Fc,i+1，则有Fc,i+1=Pi+1-Ia,i，其中Ia,i=λSi，λ经验取值为0.2。若ROi+1≥0，由水量平衡有：

Fd,i+1=Pi+1-Ia,i-Fc,i+1-ROi+1

(2)

否则Fd,i+1=0。另外，Fd,i+1反映了i到i+1时段土壤含水量的增量，即ΔW=Fd,i+1。而Si的更新公式为：

Si+1=Si-ΔW+ETi+1

(3)

式中：ETi+1为蒸散发，mm。其计算公式如下：

(4)

式中：Ei+1为实测水面蒸发，mm；Sabs为绝对可能最大滞留量，mm。

模型地面汇流采用线性水库的方法，计算公式如下：

DOi+1=d1ROi+d2DOi

(5)

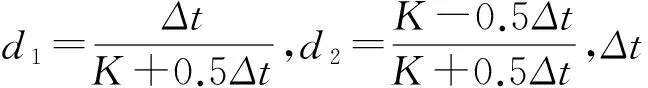
另外，该模型中还加入了地下径流汇流计算：

OBi+1=g1Fc,i+g2OBi

(6)

式中：g1和g2为汇流系数；Kb为地下径流调蓄系数。

流域总径流计算为：

Qi=DOi+OBi

(7)

模型共4个参数：Sabs，Fc，K和Kb。在湖北省地区，Sabs=90 mm，地下径流采用经验公式计算得到，不考虑蒸发计算，即模型计算中ET=0，只采用SCS模型计算地面径流部分，故只需率定两个参数：Fc，K。

1.3 模型评价指标

由于小流域缺乏实测降雨及其对应流量资料，但在设计暴雨产汇流生成设计洪水时，隐含了前期影响雨量较湿润(Pa=0.8Im)的假定，可作为特例估计模型参数。因此选取由暴雨等值线图确定出典型暴雨历时雨量和参数，求得的1%、2%、5%、10%、20%和50%设计暴雨以及对应的设计洪水过程作为二水源新安江模型和SCS模型的输入资料。采用SCE-UA最优算法对二水源新安江模型和SCS模型参数进行参数率定，适当考虑对洪峰的模拟。模型评价采用确定性系数[NSE，见式(8)]、水量平衡系数和洪峰合格率来描述。即：

(8)

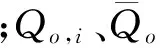
2 实例研究

2.1 研究区概况

湖北省宜昌市点军区有土城乡、联棚乡、艾家镇、桥边镇和点军街道办事处共4个乡镇和1个街道办事处，1986年设区，以境内点军坡而得名为点军区。此次山洪灾害的评价对象是以自然村为单位的，共计30个评价对象(图3)。

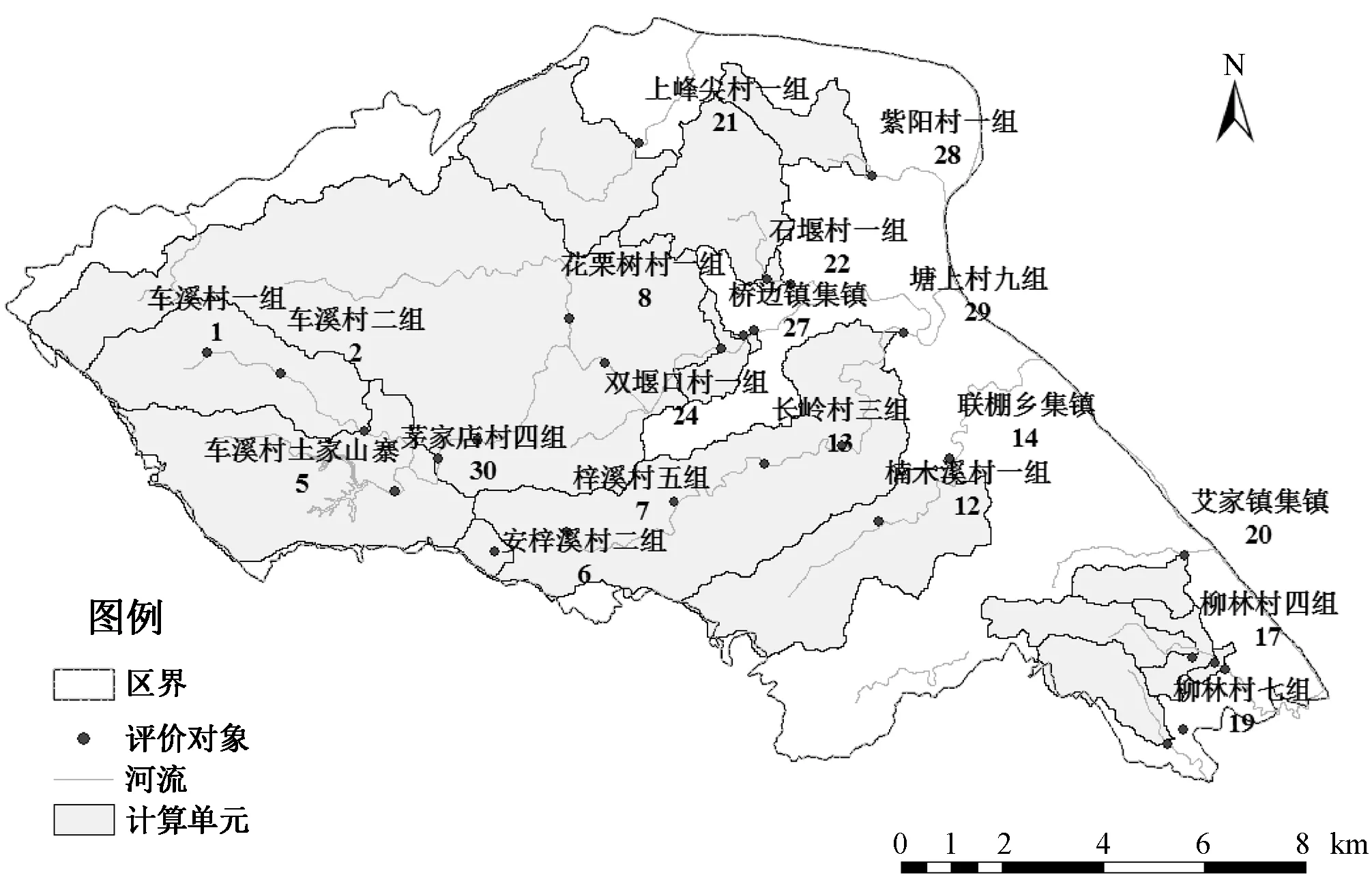
图3 点军区分析评价对象空间分布图Fig.3 Spatial distribution of objectsevaluated in Dianjun District

宜昌市点军区属中亚热带季风气候，四季分明，雨量充足，气候温和。年平均气温为16.9 ℃，最热月份为7月，最冷月份为1月。春早、夏热、秋迟、冬暖，夏季降水集中，雨热同季，四季分明。点军区年平均气温16.9 ℃，极端最低气温9 ℃，极端最高气温41.4 ℃；历年平均降水量1 165.8 mm。

2.2 计算结果

在30个评价对象中，根据小流域面积大小，选取点军街道办紫阳村一组、桥边镇上峰尖村一组、土城乡花栗树村一组和桥边镇双堰口村一组4个自然村作为典型小流域进行结果分析，典型小流域的二水源新安江模型和SCS模型的计算结果见表1；并将模型的模拟流量与设计流量过程进行对比，如图4所示。可见，选取的典型小流域的洪峰值均模拟较好，二水源新安江模型模拟效果优于SCS模型。

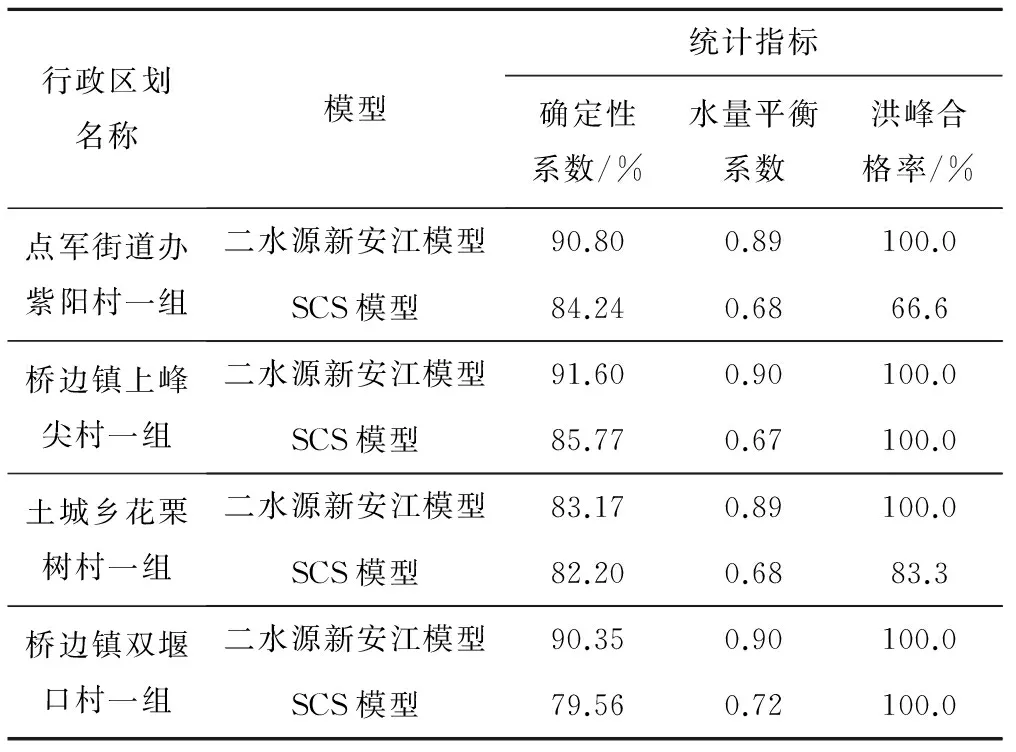
表1 新安江模型和SCS模型结果比较Tab.1 The performance of comparison between Xin'an Jiang and SCS models

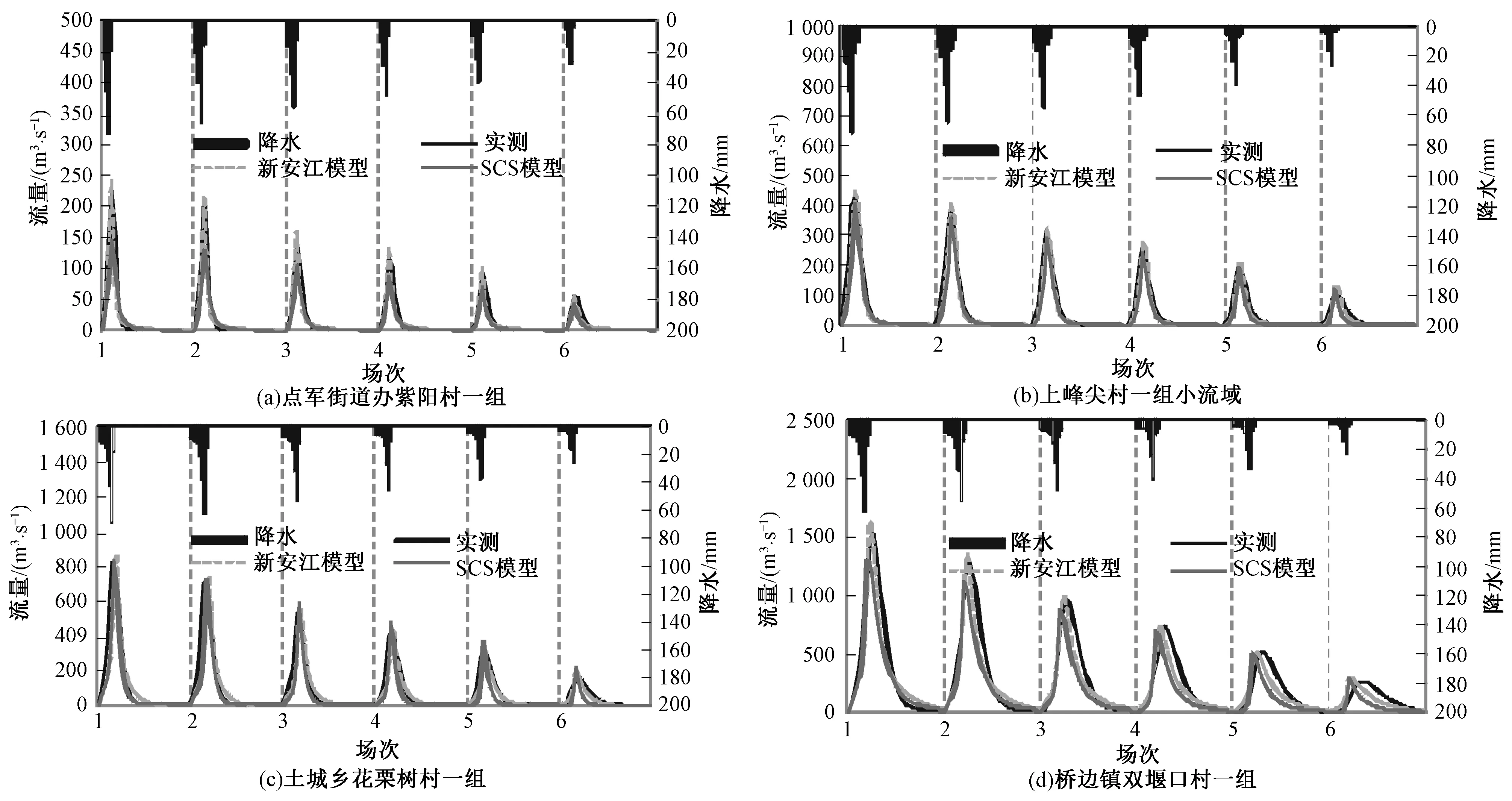
图4 模拟流量与设计流量过程线Fig.4 Comparison of runoff simulations between the SWAT and Xin'anjiang models

根据第2节临界雨量的推求步骤，试算得到4个典型小流域的临界雨量如表2所示，其临界雨量的范围为77～167 mm。根据历史洪水调查情况：点军区在1983年5月21日发生的洪水灾害，过程降雨量为141 mm；在1987年5月26日发生的洪水灾害，过程降雨量为80 mm；在1996年7月4、5日发生的洪水灾害，过程降雨量为250 mm；在1996年9月16日发生的洪水灾害，过程降雨量为140 mm；在2002年6月8日发生的洪水灾害，过程降雨量为178 mm；在2007年6月22日发生的洪水灾害，过程降雨量为103 mm；在2008年7月20日发生的洪水灾害，过程降雨量为166 mm；在2010年7月15日发生的洪水灾害，过程降雨量为122 mm。可知，历史上发生的几场洪水的过程雨量在80～250 mm之间，说明累计雨量达到80 mm左右时，有可能发生山洪灾害，累计雨量达到140 mm左右时，很可能发生山洪灾害，因此临界雨量成果基本合理。

表2 点军区典型小流域雨量临界雨量成果表Tab.2 The critical precipitation of typical watershed in Dianjun District

由于缺乏流域尺度土壤含水量的基础资料，山洪灾害分析评价采用前期影响雨量作为反映流域土壤含水量的间接指标。最终得到前期影响雨量Pa分别为干燥(Pa=0.2Im)、一般湿润(Pa=0.5Im)和湿润(Pa=0.8Im)3种情形下临界雨量计算成果如图5所示。可知，临界雨量与小流域的面积没有明显的相关关系。因为，临界雨量的推求是将相应小流域的成灾流量作为试算终点，而各小流域的成灾流量重现期的不同，导致了流域间临界雨量的差异。与流域面积不同，临界雨量的大小还取决于土壤含水量，随着土壤含水量的增加(从0.2Im到0.8Im)，同一预警时段的临界雨量逐渐减小，即土壤越湿润，临界雨量越小，发生山洪灾害的可能性越大。

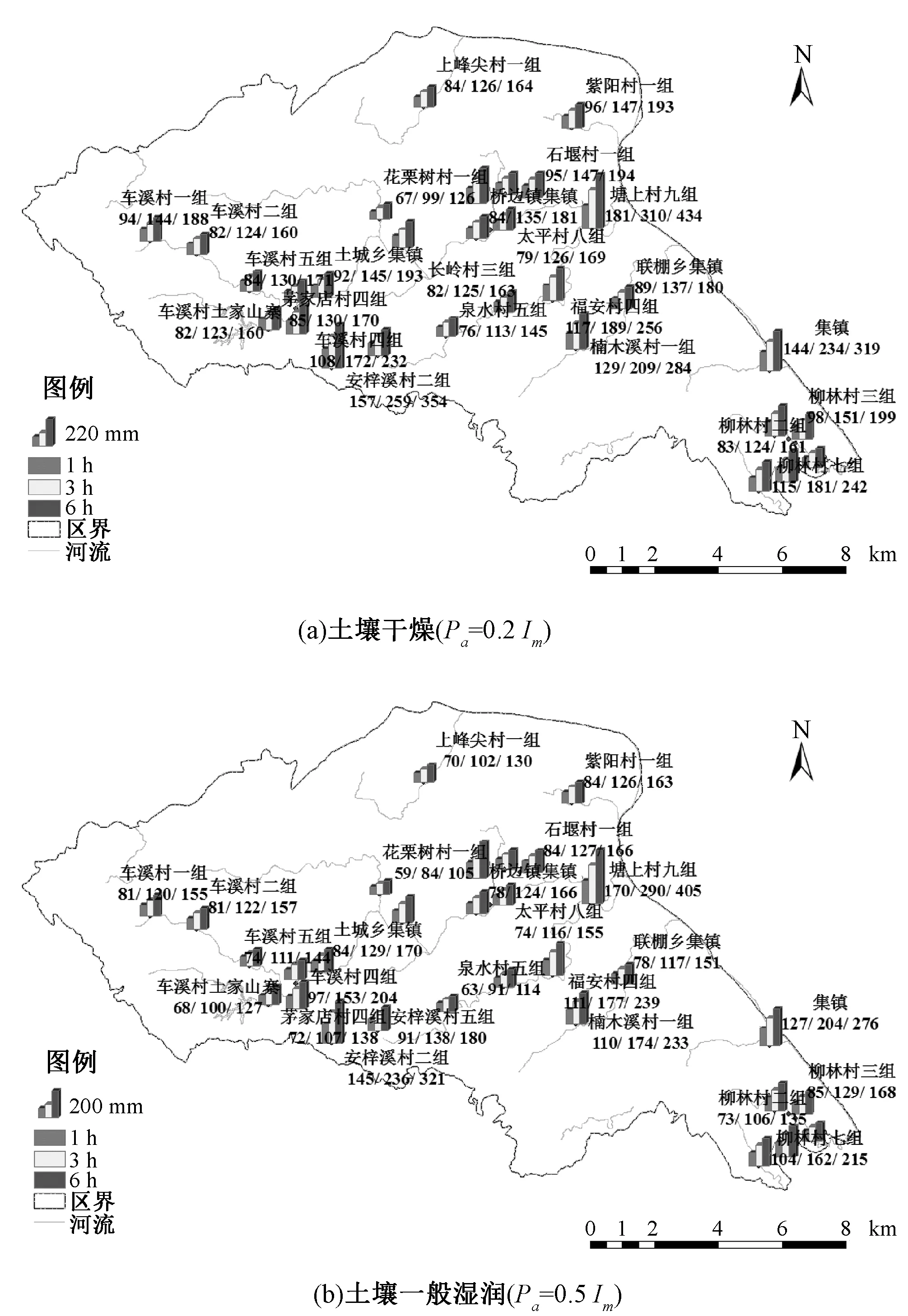
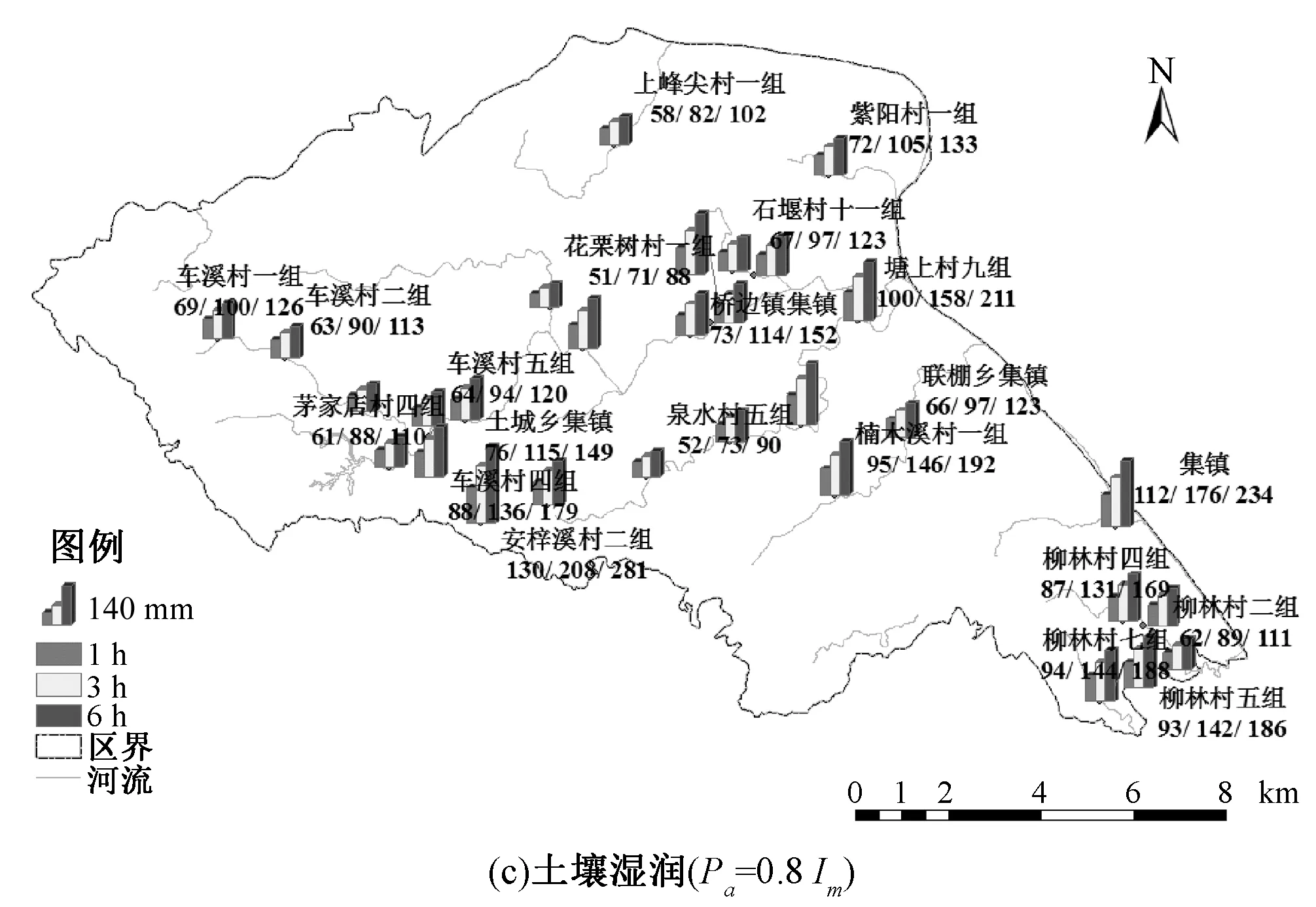
图5 点军区防灾对象临界雨量分布图(单位：mm)Fig.5 Spatial distribution map of critical precipitation for objects evaluated in Dianjun District

3 结 语

本文山洪灾害分析评价采用了模型分析法计算临界雨量，得出如下结论。

(1)以设计暴雨与相应的设计洪水为基础，对无资料地区山洪灾害临界雨量进行计算具有可行性。

(2)对于湖北省宜昌市点军区，二水源新安江模型较SCS模型模拟精度高，更适合于临界雨量计算。

(3)临界雨量的大小与土壤含水量有关，随着土壤含水量的增加，同一预警时段的临界雨量逐渐减小，即土壤越湿润，临界雨量越小，发生山洪灾害的可能性越大。

应该看到，可以采用其他方法计算临界雨

量，如经验估计法和降雨分析法，并进行以上3种方法的对比分析，以确定最适合防灾对象的临界雨量计算方法，从而提高预警的精度及可靠性。

□

[1] 叶金印, 李致家, 常 露. 基于动态临界雨量的山洪预警方法研究与应用[J]. 气象, 2014,40(1):101-107.

[2] 全国山洪灾害防治规划领导小组.山洪灾害临界雨量分析计算细则[Z].2003.

[3] 陈桂亚, 袁雅鸣. 山洪灾害临界雨量分析计算方法研究[J]. 人民长江, 2005,36(12):40-43.

[4] 段生荣. 典型小流域山洪灾害临界雨量计算分析----以黄河流域大通河支流为例[J]. 中国农村水利水电, 2008,(8):63-65.

[5] 江锦红, 邵利萍. 基于降雨观测资料的山洪预警标准[J]. 水利学报, 2010,41(4):458-463.

[6] 叶 勇, 王振宇, 范波芹. 浙江省小流域山洪灾害临界雨量确定方法分析[J]. 水文, 2008,28(1):56-58.

[7] 刘志雨, 杨大文, 胡健伟. 基于动态临界雨量的中小河流山洪预警方法及其应用[J]. 北京师范大学学报: 自然科学版, 2010,46(3):317-321.

[8] SCS. National Engineering Handbook[M].Hydrology, section4, Soil Conservation Service.US Department of Agriculture, Washington, DC, 1956.

[9] 刘家福, 蒋卫国, 占文凤, 等. SCS 模型及其研究进展[J]. 水土保持研究, 2010,17(2):120-124.

[10] Mishra S K, Singh V P. Soil conservation service cure number (SCS-CN) methodology[M]. Springer, 2010.