电动汽车变流器用IGBT水冷散热器热仿真分析

丁杰，张平



电动汽车变流器用IGBT水冷散热器热仿真分析

丁杰1, 2，张平1

(1. 湘潭大学土木工程与力学学院，湖南湘潭，411105；2. 南车株洲电力机车研究所有限公司南车电气技术与材料工程研究院，湖南株洲，412001)

以某电动汽车变流器用IGBT水冷散热器为研究对象，考虑到IGBT水冷散热器内部各槽道平均雷诺数()处于过渡区，利用FLUENT软件分别采用层流、标准−湍流模型和6种低数湍流模型计算IGBT水冷散热器的稳态结果。运用自主开发的模型降阶计算程序对IGBT水冷散热器进行瞬态问题快速计算，在验证模型降阶方法准确性的基础上，对基于中国典型城市道路工况的瞬态热仿真进行快速计算，得到IGBT元件各芯片在不同时刻的温度变化曲线。研究结果表明：该水冷散热器的散热性能满足中国典型城市道路工况的需求。

电动汽车；变流器；IGBT；水冷散热器；模型降阶；瞬态计算

为缓解能源和环境对人类生活与社会发展的压力，世界各国相继开发电动汽车[1]。变流器是电动汽车中的核心部件之一[2−3]，而IGBT水冷散热器是保证变流器乃至电动汽车安全可靠运行的关键[4−5]。由于电动汽车的运行工况复杂多变，变流器内部的IGBT元件产生的损耗不断变化，初估的某一额定工况或极限工况具有较大随意性，导致热设计工作有较多不确定性。加之汽车行业具有严格的成本控制与轻量化要求，变流器及其内部的IGBT水冷散热器的结构往往设计得非常紧凑，这给IGBT水冷散热器进行精细化热设计带来了很多困难。由于IGBT水冷散热器结构较复杂，很难通过理论或经验公式准确计算出随时间变化的瞬态温度变化结果。若采用有限体积法进行温度场的瞬态计算，则需选取较大网格尺寸来限制网格数量，否则会因庞大的计算机资源需求而导致瞬态计算相当困难；当选取较大网格尺寸生成较少数量的网格时，受流体边界层和热边界层的影响，计算结果将有较大误差，难以提高仿真结果的准确性[6]。为此，本文作者以某电动汽车变流器的IGBT水冷散热器为研究对象，利用FLUENT软件进行IGBT水冷散热器的稳态计算，并通过实验结果验证稳态仿真结果的准确性及确定合适的流动状态模型；在此基础上，运用自主开发的模型降阶计算程序对中国典型城市道路工况的瞬态热问题进行仿真计算。

1 变流器结构

某电动汽车变流器的供电来自整车高压配电和低压蓄电池，司机指令经整车控制器和CAN总线发送给变流器，从而对电机进行驱动。电机的速度和温度信息则由传感器采集后反馈给变流器。图1所示为变流器结构示意图。变流器主要由机壳、外盖、IGBT元件、水冷散热器、支撑电容、控制板组件、驱动板组件、复合母排、铜排和接线座等构成。3个型号为2MBI1400VXB-120P-50的IGBT元件安装在水冷散热器上，通过电路连接和控制策略构成逆变功能。IGBT元件在工作过程中产生的损耗占据变流器中所有电气部件损耗的绝大部分，且IGBT元件的热量基本上通过水冷散热器进行散热，因此，IGBT元件和水冷散热器是变流器热设计工作的重点。

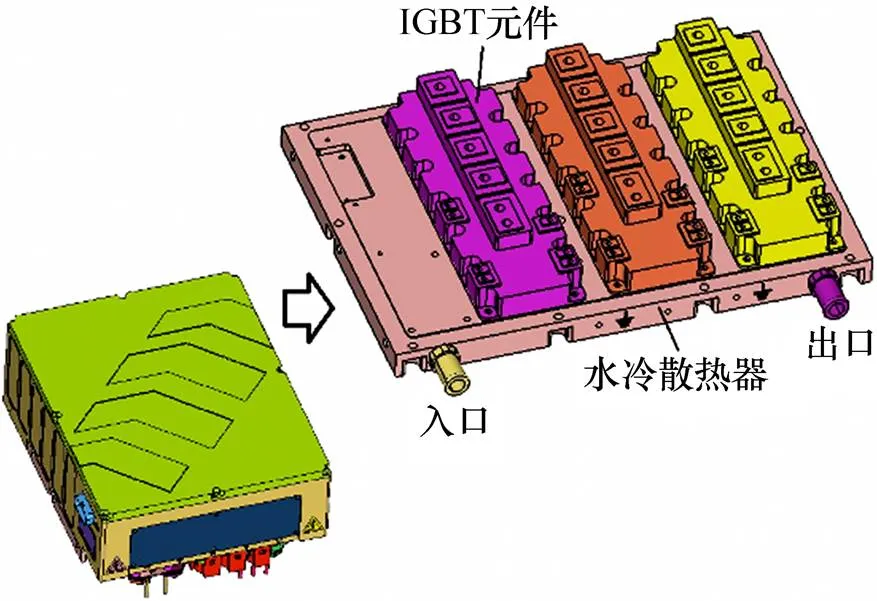
图1 变流器结构示意图

2 稳态计算

2.1 仿真模型

在利用FLUENT软件进行稳态计算之前，需要建立IGBT元件和水冷散热器的网格模型。考虑到IGBT元件各层材料的厚度均很小，且水冷散热器内部槽道宽度仅为3 mm，正方体网格边长选取0.5 mm，以便能够较准确地模拟水冷散热器内部的流动行为及边界层的影响，从而获得较准确的温度场分布。利用HyperMesh软件可以划分出以六面体为主、极少量棱柱体的高质量网格模型，划分后的网格数量为1 185万。

通过电气参数可以简单估算单个IGBT元件在额定工况下的损耗为1.127 8 kW，在极限工况下损耗为2.710 0 kW。冷却介质采用配比为50%(体积分数，下同)水和50%乙二醇的混合物，入口温度为65 ℃，入口流量为20 L/min。冷却介质的热物理参数如下：密度为1.043 t/m3，导热系数为0.378 W/(m×K)，比热容为3.345 J/(g×K)，动力黏度为1.525 g/(m×s)。通过手工计算可知该水冷散热器入口的数为18 142。槽道的截面长×宽为3 mm×15 mm。假定冷却介质均匀分配在并行的10个槽道中，可计算出槽道内的数为 2 533。根据流体力学知识可知，对于内部流动而言，当数大于10 000时，可认为是湍流区；当数大于2 300而小于10 000时，应属于过渡区；当数小于2 300时，则为层流。丁杰等[7]分析当直槽道水冷散热器内部槽道结构相同时，不同部位的流动阻力会有所区别，使得各槽道的流速不同，相应的数也会不同，导致水冷散热器内部的流动状态难以确定。在工程应用中，通常采用的标准−模型基于完全湍流的假设，故又称为高数−模型，需要对其修正以适应低数的情况。自第1种低数−模型被提出以来，先后有10余种模型被提出，不同模型之间的区别主要在于：1) 考虑壁面对湍流脉动的衰减影响；2)和方程中附加项的构造；3) 壁面上和方程边界条件的处理。由于湍流问题的复杂性高，这些模型并未给出明确的适应范围[8]。为探讨流动状态模型对仿真结果的影响，本文选取常用的层流模型和标准−模型，还有FLUENT软件提供的6种低数−模型，即Abid模型、Lan−Bremhorst模型、Launder Shorma模型、Yang−Shih模型、Abe−Kondoh−Nagano模型和Chang−Hsich−Chen模型。

2.2 流场仿真结果及分析

采用Lan−Bremhorst低数湍流模型进行计算得到的中间截面流速分布见图2。从图2可以看出冷却介质在槽道内和转折区域的流动情况，各槽道的冷却介质流速存在差异，最高流速可达2.32 m/s。冷却介质在槽道内流动时产生的压降为8.46 kPa。

2.3 温度仿真结果及分析

图3所示为采用Lan−Bremhorst低数湍流模型对额定损耗进行计算得到的带IGBT元件的水冷散热器温度场分布。从图3(a)可看出：靠近出口侧的IGBT元件芯片温度最高，为101.5 ℃。图3(b)所示为水冷散热器元件安装面的温度分布，IGBT元件安装部位的温度分布并不相同，IGBT元件端部位置出现热点，其最高温度为84.74 ℃。采用Lan−Bremhorst低数湍流模型对极限损耗进行计算可知：IGBT元件芯片最高温度为151.97 ℃，该值已超出IGBT元件所能承受的结温极限150.00 ℃，而水冷散热器元件安装面上的最高温度可达109.69 ℃。

图2 中间截面流速分布

(a) 水冷散热器整体；(b) 水冷散热器元件安装面

图4所示为冷却介质与水冷散热器固体区域接触面(流固耦合面)的对流换热系数分布，用于说明冷却介质在不同部位的热交换能力。从图4可看出：内部槽道的对流换热系数分布并不均匀，最高值1.16×104W/(m2×K)出现在冷却介质流速值高的转折区域。

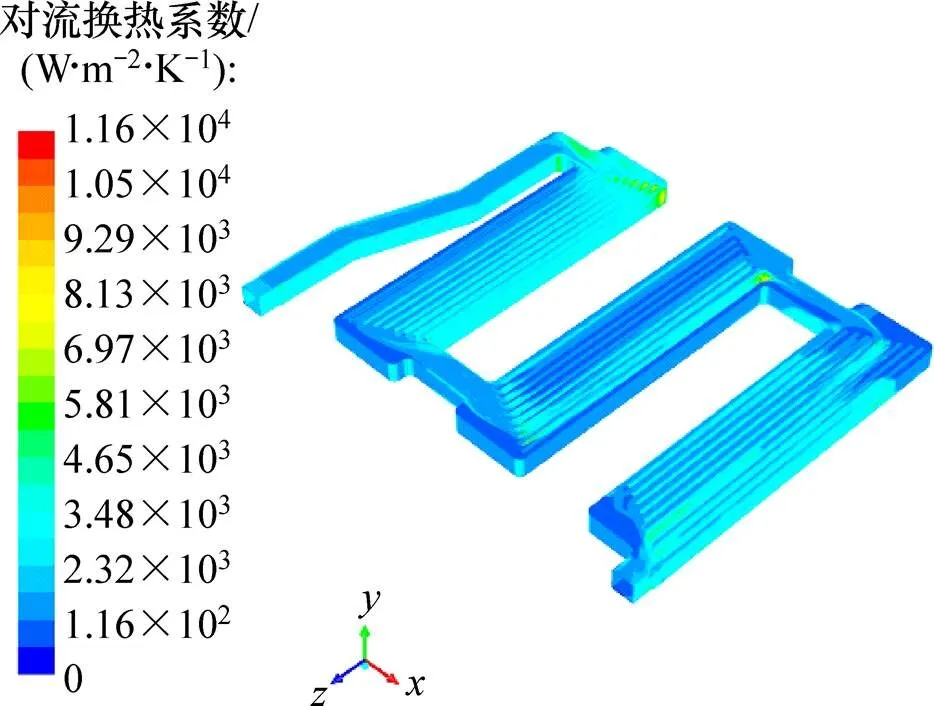
图4 对流换热系数分布

3 实验研究

3.1 实验测试

通过不同的流动状态模型计算相同工况(额定损耗或极限损耗)下的仿真结果。IGBT元件芯片最高温度相差5.9 ℃，因流动状态模型导致的芯片温升差异可达7%，压降相差0.9 kPa，这不利于水冷散热器性能评价，对变流器的热设计带来较大影响。为此，对该水冷散热器进行实验研究。

以IGBT元件为热源进行散热器热性能测试时存在以下问题：1) IGBT元件需要驱动、控制等复杂的系统组成才能正常工作；2) IGBT元件损耗特性对温度敏感，温度波动会带来一定的试验误差；3) IGBT元件属于精密器件，长时间极限工况运行很容易造成器件损伤；4) 芯片封装于绝缘材料中，不能直接测量芯片结温，在去除绝缘材料过程中很容易使IGBT元件遭受机械损伤；5) IGBT元件的价格高。这说明IGBT元件不宜直接作为水冷散热器精细实验的热源，需要采用模拟热源来代替。

在实验准备过程中，在水冷散热器安装面上钻18个直径为0.8 mm的小孔，热电偶放置在小孔中(见图5)并与水冷散热器紧密接触；在水冷散热器的模拟热源安装区域均匀涂敷一层厚约100mm的导热硅脂，用于减小接触热阻；放置模拟热源，将热电偶线从模拟热源底部的线槽中引出并逐一做好标记以示区别；最后用测力扳手将模拟热源按照规定的方式与力矩拧紧。

图5 热电偶位置

模拟热源上的电热管引线联至调压电路，可手动调节电热管的功率。水冷散热器的入口和出口接上软水管，与水泵、水箱、电磁流量计、压力表等相连，电磁流量计可以测量实验装置的流量，压力表可以测量管路系统和水冷散热器的压力1。热电偶接入数据采集器的端口，并用数据线将数据采集器的通讯端口与计算机相联，实现温度的自动采集。

受实验条件限制，很难实现水冷散热器在设计条件下所规定的入口温度与冷却液配比，因此，实验测试时大多采用室温下的纯水进行实验。测温点1，6，7，12，13和18在实验工况1(调节单个模拟热源的发热量为1.128 kW，冷却介质采用入口流量20 L/min、温度25 ℃的纯水)得到的温度曲线见图6。由图6可知：在0~100 s时，各测温点的温度迅速上升；100~300 s时，各测温点的温度上升速度明显降低；300 s之后，各测温点温度上升幅度很小，这说明温度已基本达到平衡；温度平衡时，靠近冷却水出口的测温点13温度最高，为34.1 ℃，靠近冷却水入口侧的测温点6温度最低，为30.7 ℃，其余测温点的温度处于测温点6和测温点13的温度之间。

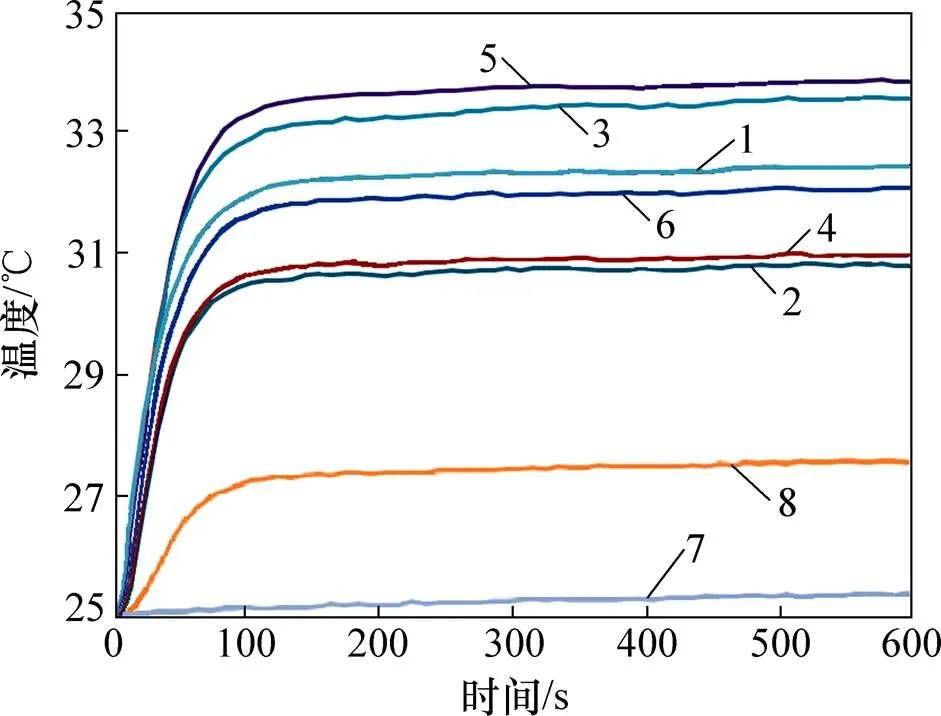
测温点编号(见图5)：1—1号；2—6号；3—7号；4—12号；5—13号；6—18号；7—入口；8—出口。

在进行水冷散热器的性能实验时，还进行了实验工况2(单个模拟热源发热量为2.050 kW、冷却介质采用入口流量为20 L/min、温度为25 ℃的纯水)、实验工况3(单个模拟热源发热量为1.143 kW、冷却介质采用入口流量为10 L/min、温度为25 ℃的纯水)、实验工况4(单个模拟热源发热量为2.066 kW、冷却介质采用入口流量为10 L/min、温度为25 ℃的纯水)、实验工况5(单个模拟热源发热量为1.153 kW、冷却介质采用入口流量为20 L/min、温度为25 ℃的50%(体积分数，下同)乙二醇、50%水)和实验工况6(实验工况5进行至590 s，迅速调节单个模拟热源发热量至2.055 kW，其余条件不变)的温升测量工作[9]。由于调压电路的变化量需要手动调节，很难在每次实验时保证完全一致，使得上述实验工况的模拟热源发热量存在一些差异。在上述温度测量过程中，还记录了整体水路系统的压力1。

为了测量水冷散热器的压降，待温升测量工作完成后，拆除水冷散热器，换成10 cm长的短接水管，此时，可以测出管路系统的压力为2。因此，水冷散热器的压降Δ应等于整体水路系统的压力1减去管路系统的压力2，即Δ=1−2。通过实验测量可知冷却介质采用温度为25 ℃的纯水，入口流量采用 10 L/min和20 L/min时的压降分别为8 kPa和21 kPa。

3.2 仿真结果与实验结果对比

利用上述实验工况1的条件作为仿真参数，参照文献[9]中方法建立模拟热源和水冷散热器的网格模型，利用不同的流动状态模型进行模拟，得到相应仿真结果。采用Lan−Bremhorst低数湍流模型得到的带模拟热源的水冷散热器温度场分布见图7。从图7(a)可看出：模拟热源上的电热管温度最高，为47.3 ℃。图7(b)所示为水冷散热器上模拟热源安装面的温度场分布，3个模拟热源安装部位的温度分布并不相同，局部热点的最高温度为36.44 ℃。

(a) 整体水冷散热器；(b) 水冷散热器模拟热源安装面

按照测温点位置提取不同流动状态模型的仿真结果，绘制成如图8所示的温度对比曲线。从图8可知：层流模型和标准−模型的各测温点温度是各种流动状态模型中的上、下限，低数湍流模型的温度稍微高于标准−模型的温度，Lan−Bremhorst模型的温度与实验温度吻合度最高；层流以及标准−，Abid，Lan−Bremhorst，Launder Shorma，Yang−Shih，Abe−Kondoh−Nagano和Chang−Hsich−Chen模型得到的水冷散热器压降分别为7.14，8.11，7.54，7.53，7.74，7.32，7.53和7.56 kPa，这些压降均小于实验结果的主要原因在于：水冷散热器的入口和出口均安装了水嘴接头，由于水嘴接头会产生较大压降，仿真时难以建立水嘴接头的仿真模型而未考虑其影响。从水嘴接头的产品数据手册可知单个水嘴接头在20 L/min纯水流过时的压降约为6.6 kPa，由此可知Lan−Bremhorst模型的压降仿真结果与实验结果接近。对基于实验工况2~6的仿真结果分别与实验结果进行对比，对比结果均可说明Lan−Bremhorst模型在该水冷散热器的稳态计算中具有好的适用性。

1—层流模型；2—Launder Shorma模型；3—标准k−ε模型；4—Lan−Bremhorst模型；5—Abid模型；6—Yang−Shih模型；

4 瞬态计算

4.1 基于模型降阶方法的快速计算程序

由于利用FLUENT软件针对网格数量多的模型进行流场与温度场计算时，需要不断地迭代计算而消耗大量的计算时间，如在DELL T7600台式工作站上进行8处理器并行计算稳态问题时，迭代3 000次基本可以达到10−6残差收敛准则，消耗的时间约为15 h，未采用并行计算时的消耗时间达62 h。为实现快速计算瞬态问题，人们对模型降阶方法进行了研究，并取得了好的应用效果[10−15]。基于Matlab软件、ANSYS软件和Krylov子空间投影法进行模型降阶并快速计算的自主开发程序流程见图9[16−17]。首先通过精细网格的FLUENT模型得到对流换热系数分布，为粗糙网格的ANSYS热传导有限元模型提供准确的边界条件。当模型中有多个热源的损耗需要改变时，依次设置每个热源的发热量为单位值，其余热源的发热量为0，再分别从这些有限元模型中提取热传导矩阵和热容矩阵文件。在Matlab软件中读取矩阵文件并整理出新的热传导矩阵(×阶)、载荷列阵(×1阶)和热容矩阵(×阶)(其中，为ANSYS热传导有限元模型的节点数目)。采用Krylov子空间投影法将×阶矩阵降阶为×阶矩阵(＜)，使用常微分方程求解器进行求解，然后将结果投影到原模型上，从而得到有限元模型每个节点在不同时刻的温度结果。重复热源设置、求解和投影等步骤，即可实现多热源变工况的瞬态计算。降阶阶数主要取决于时间步长，通常取5~50，这远小于原有阶数，从而使计算效率比ANSYS有限元计算效率高几百至几千倍，所需的计算时间和资源大大减少。

图9 快速计算程序流程

4.2 基于定值损耗的温升计算

针对IGBT元件与水冷散热器建立ANSYS热传导有限元模型时，正方体网格边长为3 mm，得到的模型网格数为23万，节点数为26万。基于前面稳态计算所述的结果，将图4所示的对流换热系数插值到ANSYS有限元模型中，进行额定损耗的稳态计算可得到温度场分布，IGBT元件上的芯片最高温度为101.117 ℃，与图3中的IGBT元件芯片最高温度101.5 ℃相比非常接近，说明对流换热系数由精细网格向粗糙网格插值处理的有效性。

以额定损耗为输入，利用自主开发程序计算0.01~1 000 s时间段的瞬态问题，经过数十秒计算即可得到有限元模型每个节点在不同时刻的温度。为便于说明瞬态计算结果，提取IGBT元件上的最高温度可绘制成如图10所示的温升曲线。由图10可知：0.01~100 s内温度迅速上升，完全稳定的温度为101.117 ℃，所需时间为310 s。稳定后的温度与ANSYS稳态计算温度完全一致，说明自主开发程序计算的准确性。

图10 以额定损耗为输入的瞬态最高温度计算结果

在以额定损耗为输入、温度稳定的情况下，以极限损耗为输入，利用自主开发程序计算0.01~1 000 s时间段的瞬态问题，提取IGBT元件上的最高温度绘制成如图11所示的温升曲线。从图11可见：其温升变化规律与图10所示的相同，完全稳定的温度为151.78 ℃；当温度由101.117 ℃到达125 ℃需5.5 s，由101.117 ℃到达150 ℃需62.6 s。这些结果有利于确定IGBT元件由额定损耗工况稳定运行情况下切换至极限损耗工况安全可靠运行的时间。

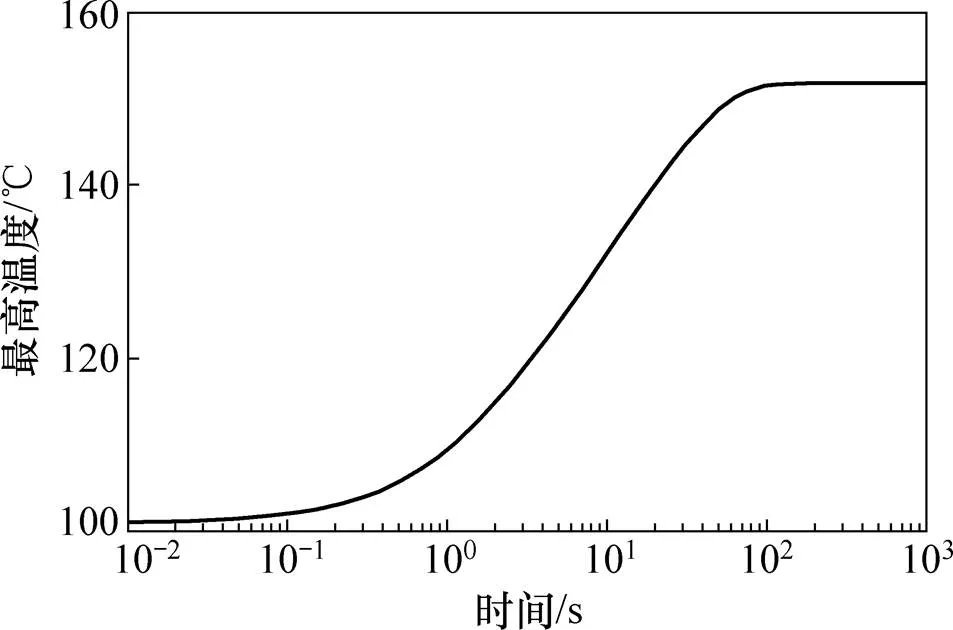
图11 以极限损耗为输入的瞬态最高温度计算结果

对模拟热源与水冷散热器建立ANSYS热传导有限元模型时，正方体网格边长为3 mm，得到的模型网格数为24万，节点数为28万。ANSYS有限元模型的稳态计算结果与FLUENT稳态计算结果相近。以实验工况1的损耗为输入，快速计算得到的温升曲线与图6的实验温升曲线规律基本一致。

4.3 基于中国典型城市道路工况的温升计算

公交运营具有频繁起步和停车、发动机长时间处于怠速工况、低速重载和持续运行等特点。以中国典型城市道路工况[18]进行主电路仿真，可以得到如图12所示的不同时刻电气参数(如电机相电压、电机电流、功率因数和输出频率)，由此可进一步计算出不同时刻的IGBT芯片损耗和二极管芯片损耗[19](见图13)。将IGBT元件的芯片损耗作为自主开发程序的输入，经过10余min计算可以得到3个IGBT元件的芯片温度变化曲线(见图14)。由于不同时刻的电气参数发生变化，产生的损耗相应发生变化，与之对应的芯片温度亦发生改变。在基于中国典型城市道路工况运行过程中，芯片温度未超过115 ℃，说明该水冷散热器的散热性能可以满足中国典型城市道路工况的需求。此外，所得的瞬态温升结果可为后续IGBT模块疲劳寿命预估提供依据。由于在计算过程中得到有限元模型每个节点在不同时刻的温度，可为全面深入分析模型不同部位的温升变化提供依据。

(a) 电机电流；(b) 输出频率；(c) 电机相电压；(d) 功率因数

图13 单个IGBT元件的损耗变化曲线

图14 3个IGBT元件的芯片温度变化曲线

5 结论

1) 通过层流模型、标准−模型和6种低数湍流模型的稳态计算结果与实验结果对比分析，结果表明Lan−Bremhorst低数湍流模型在该水冷散热器中具有较强适用性。

2) 采用对流换热系数插值方法可以保证网格数目较少的ANSYS热传导有限元模型能获得与网格数目多的FLUENT模型基本一致的温度。

3) 基于模型降阶方法的快速计算自主开发程序不仅具有很高的计算效率，而且可准确得到与实验测试的温升具有相同变化规律的计算结果。

4) 基于中国典型城市道路工况的瞬态热仿真计算可以获得不同时刻的芯片温度，水冷散热器的散热性能满足中国典型城市道路工况的需求，计算温度较基于初估的某一额定损耗和极限损耗得到的稳态温度更具现实意义。

[1] 杨卫华. 电动汽车永磁同步电动机及其控制器研究[D]. 武汉: 湖北工业大学电气与电子工程学院, 2009: 1−12. YANG Weihua. Research on permanent magnet synchronous motor and its controller in electric vehicle[D]. Wuhan: Hubei University of Technology. School of Electrical and Electronic Engineering, 2009: 1−12.

[2] 杨利辉. 电动汽车驱动变流器的优化设计[D]. 重庆: 重庆大学电气工程学院, 2004: 25−34. YANG Lihui. Optimized design of electric vehicle drive-motor controller[D]. Chongqing: Chongqing University. School of Electrical Engineering, 2004: 25−34.

[3] 邵桂欣, 张承宁. 电动汽车用续流增磁变流器温升的改善方法[J]. 微电机, 2007, 40(11): 29−31. SHAO Guixin, ZHANG Chengning. Improvement elevated temperature of enhanced magnetism motor controller applied to electrics vehicles[J]. Micromotors Servo Technique, 2007, 40(11): 29−31.

[4] 张舟云, 徐国卿, 沈祥林. 用于电动汽车的电机和驱动器一体化冷却系统[J]. 同济大学学报(自然科学版), 2005, 33(10): 1367−1371. ZHANG Zhouyun, XU Guoqing, SHEN Xianglin. Uniform cooling system of motor and its controller used in electric vehicles[J]. Journal of Tongji University (Natural Science), 2005, 33(10): 1367−1371.

[5] 乐智. 纯电动汽车电机驱动系统的冷却系统设计与研究[D]. 天津: 河北工业大学机械工程学院, 2010: 23−32. YUE Zhi. Design and research on the cooling system of pure electric vehicle motor drive system[D]. Tianjin: Hebei University of Technology. School of Mechanical Engineering, 2010: 23−32.

[6] 丁杰, 唐玉兔, 忻力, 等. 网格尺寸对IGBT水冷散热器仿真结果的影响[J]. 大功率变流技术, 2012(6): 26−30. DING Jie, TANG Yutu, XIN Li, et al. Effects of mesh size on simulation results of water-cooling radiator for IGBT module[J]. High Power Converter Technology, 2012(6): 26−30.

[7] 丁杰, 李江红, 陈燕平, 等. 流动状态与热源简化方式对IGBT水冷板仿真结果的影响[J]. 机车电传动, 2011(5): 21−25. DING Jie, LI Jianghong, CHEN Yanping, et al. Effects of flow regime and heat source simplifications on simulation results for water-cooling plate of IGBT[J]. Electric Drive for Locomotives, 2011(5): 21−25.

[8] 陶文铨. 数值传热学[M]. 2版. 西安: 西南交通大学出版社, 2001: 332−409. TAO Wenquan. Numerical heat transfer[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2001: 332−409.

[9] 丁杰, 张平. 电机控制器用IGBT水冷散热器温升实验与热仿真[J]. 大功率变流技术, 2015(3): 23−28. DING Jie, ZHANG Ping. Temperature-rise test and thermal simulation for IGBT water-cooled radiator of motor controller[J]. High Power Converter Technology, 2015(3): 23−28.

[10] WILHELMUS H A S, HENK A V, JOOST R. Model order reduction: theory, research aspects and applications[M]. Berlin:Springer, 2008: 1−72.

[11] 关乐, 褚金奎, 齐东周, 等. 面向MEMS系统级仿真的宏模型研究[J]. 系统仿真学报, 2009, 21(15): 4561−4567. GUAN Le, CHU Jinkui, QI Dongzhou, et al. Review of research on macromodel for MEMS system-level simulation[J]. Journal of System Simulation, 2009, 21(15): 4561−4567.

[12] RUDNYI E B, KORVINK J G. Model order reduction for large scale engineering models developed in ANSYS[J]. Lecture Notes in Computer Science, 2006, 3732(1): 349−356.

[13] YANG Y J, YU C C, SHEN K Y. MEMS heat transfer arnoldi-based macromodels and the study of minimum required orders[J]. Tamkang Journal of Science and Engineering, 2005, 8(3): 185−190.

[14] 齐东周, 褚金奎, 关乐. MEMS降阶宏模型仿真平台研究[J]. 微计算机信息, 2009, 25(3): 185−187. QI Dongzhou, CHU Jinkui, GUAN Le. On the tool of MEMS CAD system-level simulation[J]. Microcomputer Information, 2009, 25(3): 185−187.

[15] 蒋耀林. 模型降阶方法[M]. 北京: 科学出版社, 2010: 77−122. JIANG Yaolin. Model order reduction method[M]. Beijing: Science Press, 2010: 77−122.

[16] 丁杰, 唐玉兔. 模型降阶方法在瞬态热仿真中的应用[J]. 机车电传动, 2014(5): 51−55. DING Jie, TANG Yutu. Application research of model order reduction method in transient thermal analysis[J]. Electric Drive for Locomotives, 2014(5): 51−55.

[17] 丁杰, 唐玉兔, 忻力, 等. 输出频率对IGBT元件结温波动的影响[J]. 电气传动, 2014, 44(6): 76−80. DING Jie, TANG Yutu, XIN Li, et al. Effects of output frequency on junction temperature ripple for IGBT module[J]. Electric Drive, 2014, 44(6): 76−80.

[18] 汪伟, 刘凌. 电动公交客车动力总成技术的发展及展望[J]. 大功率变流技术, 2012(2): 1−4. WANG Wei, LIU Ling. Development and prospect of powertrain technology for electric bus[J]. High Power Converter Technology, 2012(2): 1−4.

[19] 丁杰, 忻力, 何海兴, 等. 二电平IGBT变频器载荷工况下的损耗和温升计算程序开发[J]. 大功率变流技术, 2014(1): 1−4. DING Jie, XIN Li, HE Haixing, et al. Program development of losses and temperature rise for two-level IGBT converter under loading conditions[J]. High Power Converter Technology, 2014(1): 1−4.

(编辑 陈灿华)

Thermal analysis of IGBT water-cooling radiator for electric vehicle converter

DING Jie1, 2, ZHANG Ping1

(1. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China;2. CSR Research of Electrical Technology & Material Engineering,CSR Zhuzhou Institute Co. Ltd., Zhuzhou 412001, China)

An IGBT water cooling radiator used in an electric vehicle converter was studied. Considering that the average Reynolds number of each channel was in the transition region, steady state temperature of the radiator was calculated by using the laminar model, the standard-turbulence model and six kinds of different low Reynolds number turbulence models with FLUENT software, respectively. Transient problem of the radiator was calculated by using self-developed model order reduction calculation program. Through verifying the accuracy of model order reduction method, transient thermal simulation of typical Chinese urban road conditions was carried out to obtain the temperature variation curves of each chip in IGBT device at different time. The results show that the heat dissipating performance of the water cooling radiator can meet the demand of typical Chinese urban road conditions.

electric vehicle; converter; IGBT; water-cooling radiator; model order reduction; transient calculation

10.11817/j.issn.1672−7207.2017.02.033

U464.138

A

1672−7207(2017)02−0525−08

2016−02−13；

2016−04−20

湖南省自然科学省市联合基金重点资助项目(12JJ8020)(Project(12JJ8020) supported by the Hunan Province and Municipal Joint Key Natural Science Foundation)

丁杰，博士研究生，高级工程师，从事一般力学与力学基础、变流器结构仿真与热仿真研究；E-mail：dj8083@126.com