框架填充墙等效单杆斜撑简化模型

邓宏宇，孙柏涛



框架填充墙等效单杆斜撑简化模型

邓宏宇1, 3，孙柏涛1, 2

(1. 哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨，150001；2. 中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨，150080；3. 东北农业大学水利与土木工程学院，黑龙江哈尔滨，150030)

在已有的填充墙等效对角斜撑模型的基础上，结合近年来地震现场普遍出现的填充墙顶部与框架梁柱节点接触处的砖砌体在大震作用下通常会被压碎这一实际震害现象，改变等效斜撑杆与框架柱的接触位置，提出一种新的简化计算模型。通过理论推导给出等效斜撑墙片宽度的计算公式，利用ABAQUS有限元模拟的方法，确定等效斜撑墙片与框架柱合理接触位置的经验计算公式。最后通过将简化有限元模型计算结果与试验结果进行对比，验证该简化建模方法的正确性。研究结果表明：传统的对角斜撑模型低估框架填充墙构件的水平承载力，新模型与芦山地震框架结构震害结果更相符。本模型可为框架结构抗震分析与设计验算提供参考意义。

填充墙；框架结构；等效斜撑模型；抗剪承载力；刚度

钢筋混凝土框架填充墙结构是我国应用最广泛的结构形式之一，近年来发生的地震中，由于填充墙与框架梁柱之间相互作用造成的震害十分严重[1]。为研究框架填充墙结构的破坏机理，人们常常需要用数值模拟的方法，建立有限元模型进行分析和计算。因此，研究与框架填充墙构件实际受力最为接近的有限元模型的建模方法意义十分重大。在地震工程领域，大致有2类建模方法：一是微观模型，即采用实体单元精细化模型，这种模型能够精确的模拟填充墙体的变形、开裂和与框架梁柱的局部应力作用，但也存在单元个数多、计算量大和不容易收敛的问题，无法应用于整体模型的大规模计算。二是宏观等效模型，即基于一定的假设，将填充墙简化为等效斜撑杆来模拟计算。等效斜撑的概念由POLYAJCOV[2]基于试验提出，他认为填充墙可以简化为在填充墙对角线方向上只受压不受拉的斜撑杆。由于等效对角斜撑模型概念简单、便于应用、宏观上描述了填充墙与框架之间的相互作用，因此在国内外有广泛的应用。但该模型也存在一些明显的不足，该计算模型等效斜撑杆的位置与填充墙对角线方向重合，上部杆端作用在梁柱节点处，这在弹性阶段或者构件刚进入弹塑性阶段是合理的。但是近年来的震害实际和框架填充墙构件的拟静力推覆试验表明[3]：在大震作用下，填充墙顶部与梁柱节点接触处的角部砖砌体通常会被压碎从而退出工作，这一破坏形式在地震现场比较普遍[4]。针对大震中框架结构这种较常出现的破坏模式，在极限承载力条件下，仍按等效斜撑杆端支撑在梁柱节点处来处理是不尽合理的，用该方法建立的模型来模拟结构在弹塑性阶段的地震反应与地震现场看到的实际的震害不符，因为填充墙体顶部退出工作时墙体实际支撑位置下移，使得框架节点与支撑位置的部分框架承受很大的剪力，经常造成框架根部剪切破坏或节点破坏。对于等效斜撑模型，最重要的参数就是确定等效斜撑墙片的有效宽度，国内外的研究学者给出了多种计算方法。其中，HOLMES[5]建议等效斜撑墙片的有效宽度取填充墙对角线长度的1/3；SMITH等[6]通过理论分析引入相对刚度参数的概念，认为等效墙片宽度与框架和填充墙的刚度比有关；SANEINEJAD等[7]考虑了结构的非线性，修正了单个等效支撑的面积公式，将等效墙片的有效宽度用与框架梁柱接触长度的方式来表示；TUCKER[8]通过一系列的框架填充墙构件的试验，对比了18个等效斜撑宽度的计算公式，得出了1个较适合钢筋混凝土框架砌体填充墙构件的等效斜撑宽度公式。由此可见，不同的学者给出的计算公式差别很大，等效斜撑墙片宽度的取值有待于研究。基于以上的研究现状，本文作者从实际工程应用的角度出发，在传统的对角斜撑模型的基础上，调整斜撑杆端与框架柱的接触位置，将斜撑杆上端自梁柱节点处下移某一距离，提出一种新的等效单杆斜撑模型。结合理论分析和有限元模拟的方法，给出等效斜撑墙片宽度和等效斜撑杆与框架柱合理的接触位置的计算公式。该简化模型适用于大震作用下，在非线性阶段，填充墙角部砌体被压碎这一普遍出现的破坏模式，可应用于整体结构大规模的分析计算。

1 震害实例

1.1 结构破坏情况

2013−04−20T08:02，中国四川省雅安市芦山县发生7.0级地震，震源深度13 km，震中烈度为Ⅸ度。地震造成大量的人员伤亡和房屋建筑破坏。本文作者在第一时间进入雨城区上里镇进行震害考察，发现该地区钢筋混凝土框架结构的震害十分严重。尤其是教学楼结构，多采用单跨外廊式的钢筋混凝土框架结构。图1所示为芦山地震雨城区上里中学教学楼震害情况。在地震作用下，框架柱柱头受剪破坏，填充墙严重开裂破坏，填充墙与框架梁柱节点处的角部砖砌体被压碎。这种破坏形式在震区框架结构建筑中十分普遍[9]。为研究框架填充墙构件的受力机制和破坏机理，下面用ABAQUS有限元模拟的方法，模拟计算图1所示的框架填充墙构件。

1.2 实体单元模型

首先，通过ABAQUS有限元软件建立框架填充墙构件的实体单元有限元模型。有研究表明，实体单元模型的计算结果与实际构件最为接近[10]。为验证实体单元计算结果的准确性，根据MEHRABI等[11]所做的一系列框架填充墙构件模型拟静力试验，模拟其中的构件1、构件8和构件9，并将有限元计算结果与通过试验所得实际数据进行对比。其中构件1为空框架，构件8为空心砌块填充墙，构件9为实心砖填充墙，相关的试件尺寸和材料参数见文献[11]。

ABAQUS中建模过程如下：框架梁柱采用实体单元C3D20R，钢筋采用桁架单元T3D2，本构关系选择对应的混凝土和钢筋塑性本构[12]，填充墙采用实体单元C3D20R，本构关系采用砌体塑性本构[13]，将材料的本构关系赋予到ABSQUS中的混凝土损伤塑性模型进行弹塑性的静力模拟分析。钢筋与混凝土框架梁柱之间采用embedded连接，填充墙与框架梁柱之间采用contact连接模拟填充墙与框架梁柱之间的相互作用。采用隐式静力分析的方法，在梁端施加侧向荷载，最终能够得到1条荷载−位移曲线见图2。

(a) 框架填充墙破坏；(b) 填充墙角部被压碎

从图2中试件荷载−位移曲线的试验值与各自对应的实体单元有限元模拟值的对比可以看出：2条曲线的最大水平承载力值比较吻合，验证了采用实体单元有限元模型静力分析得到的构件的最大水平承载力模拟结果与实际相符。因此，在后续的分析过程中，认为实体单元模型的计算结果即为构件的实际值。

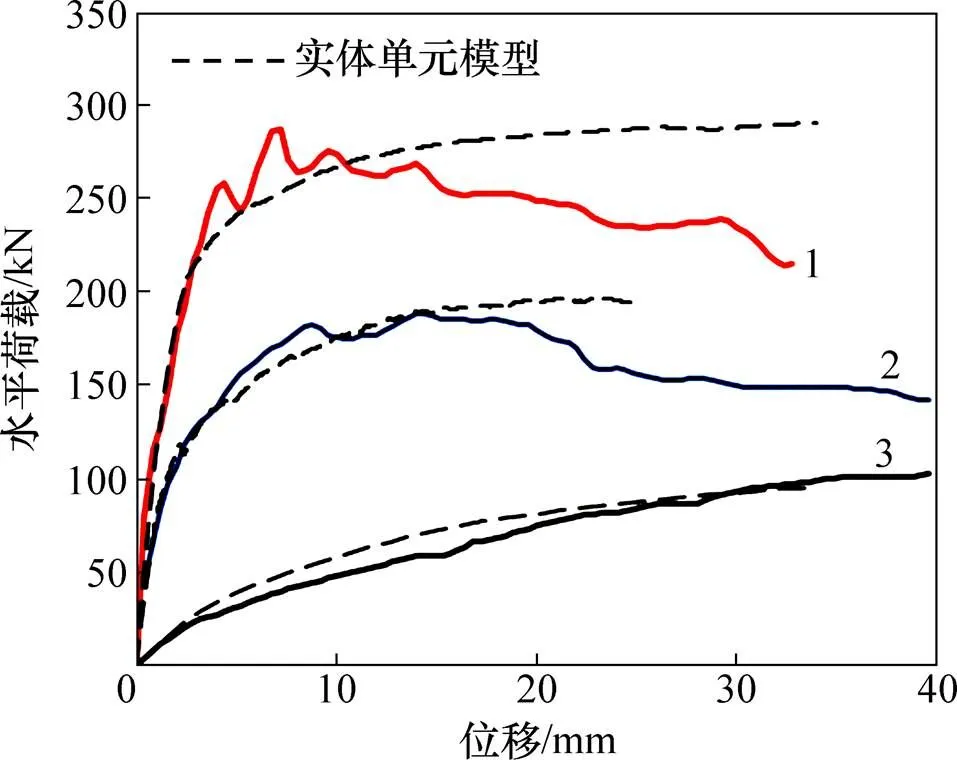
1—实心砖填充墙；2—空心砌块填充墙；3—空框架。

1.3 震害实例计算结果

将图1中的框架填充墙构件单独提取出来，采用已验证的实体单元有限元建模方法对其进行模拟计算分析，并将计算结果与实际结果进行对比。图3所示为构件达到极限水平承载力后某一时刻的Mises应力云图。

从图3(a)可以看出：随着框架填充墙构件侧向变形的增加，填充墙右上角的砖砌体受到框架梁柱节点的挤压，当超过砌体材料的极限变形能力时，砖砌体就会因为压碎而退出工作。从填充墙的Mises应力云图可以看出填充墙中应力的分布和变化趋势，在初始阶段，填充墙右上角的角部砖砌体应力最大，对角斜撑的作用比较明显。当位移进一步增大时，角部的最大应力会有一定程度的下移(图3(b))，此时对角斜撑模型不再适用。图3(c)中，从框架柱与填充墙接触面的压应力变化也可以看出，最大应力的位置随着框架侧向位移的增大而逐渐下移。以上计算结果最终状态与实际震害比较相符，说明高烈度区的结构遭到大震作用时，填充墙对框架的对角斜撑位置有一定的下移，原来始终保持在对角线方向上的对角斜撑模型不尽合理，应对模型进行改进和调整，才能更好地适用非线性阶段的模拟分析。

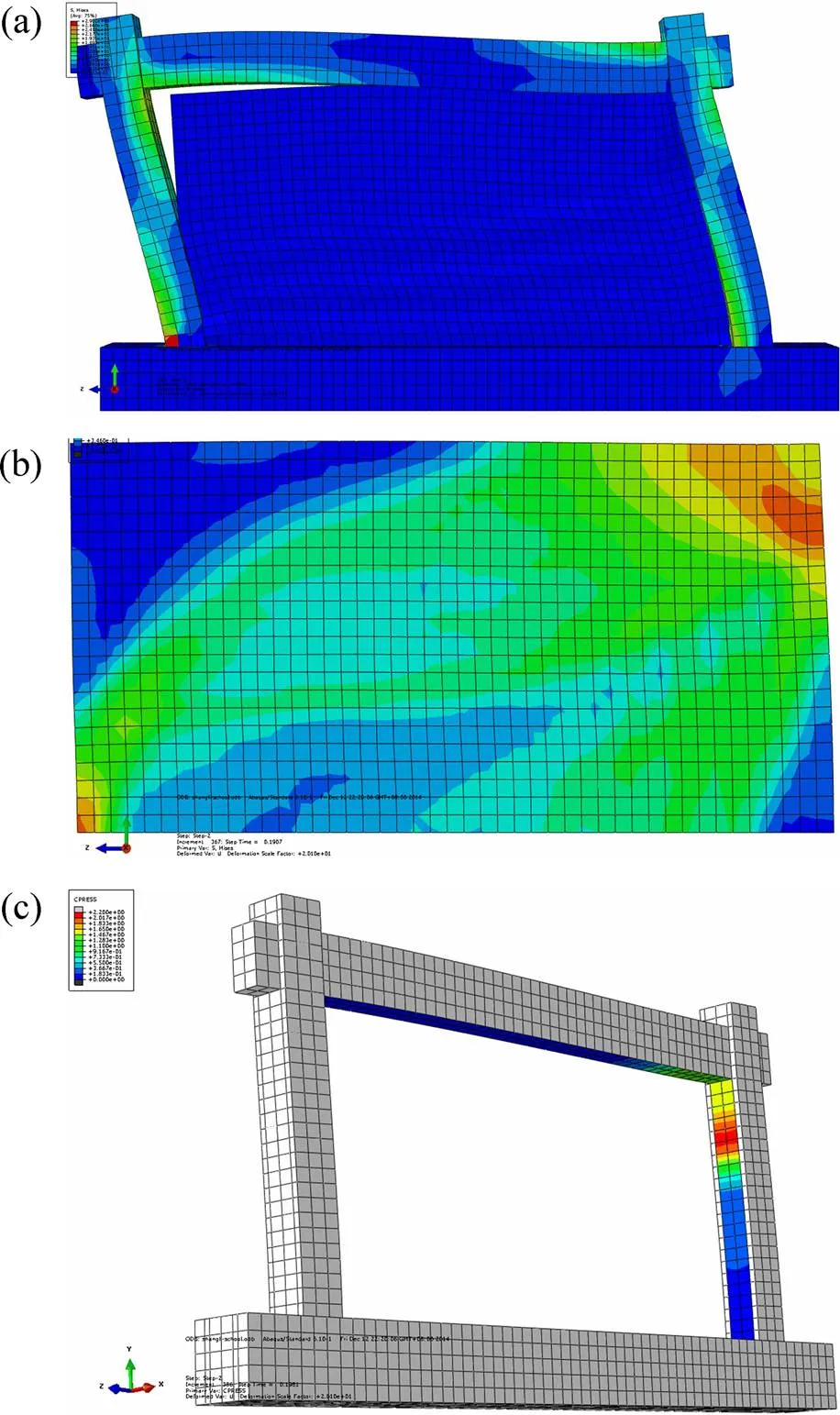
(a) 整体Mises应力云图；(b) 填充墙Mises应力云图；(c) 接触面处压应力变化

基于以上的实际震害和有限元模拟的初步分析，提出一种适用于普遍出现的填充墙角部砌体被压碎的受力模型，根据该模型，从受力分析的角度，推导出等效斜撑墙片宽度的计算公式，并通过设计一系列构件对其计算结果进行统计回归，给出等效斜撑杆与框架柱接触位置的经验计算公式。

2 等效斜撑墙片宽度

2.1 计算简图和基本假设

单榀框架填充墙构件的计算简图如图4所示，在地震荷载作用下，认为只有一定宽度的斜撑墙片参与受力，其与框架柱的接触长度为c，墙片厚度与填充墙厚度相同，等效斜撑墙片的中轴线与水平方向的夹角为′。针对该模型，做出如下基本假设：1) 普通砖砌体填充墙为各向同性的理想匀质材料。2) 在以下的受力分析中，为简便起见假设填充墙的边界与框架梁柱的中轴线一致，即′≈，′≈，其中′和′为框架轴线处的高度和跨度，和为填充墙的高度和跨度。3) 简化的斜撑填充墙顶部在构件进入极限承载力，角部砖砌体被压碎之后认为与梁没有接触，此时斜撑墙片的顶端与框架梁之间存在一定的距离，且与柱的接触长度不超过0.3倍填充墙高，见式(1)。4) 框架柱、框架梁内最大弹性弯矩与屈服弯矩的比值不超过0.2[14]。见下式：

c≤0.3(1)

≤(2)

式中：c为等效斜撑墙片与框架柱的接触长度与框架柱高度的比值；为填充墙的高度；c和b为框架柱、框架梁的最大弹性弯矩；pc和pb分别为框架柱、框架梁的屈服弯矩；c和b分别为框架柱、框架梁内弹性弯矩与屈服弯矩的比值；0为框架柱、框架梁内弹性弯矩与屈服弯矩的比值最大值。

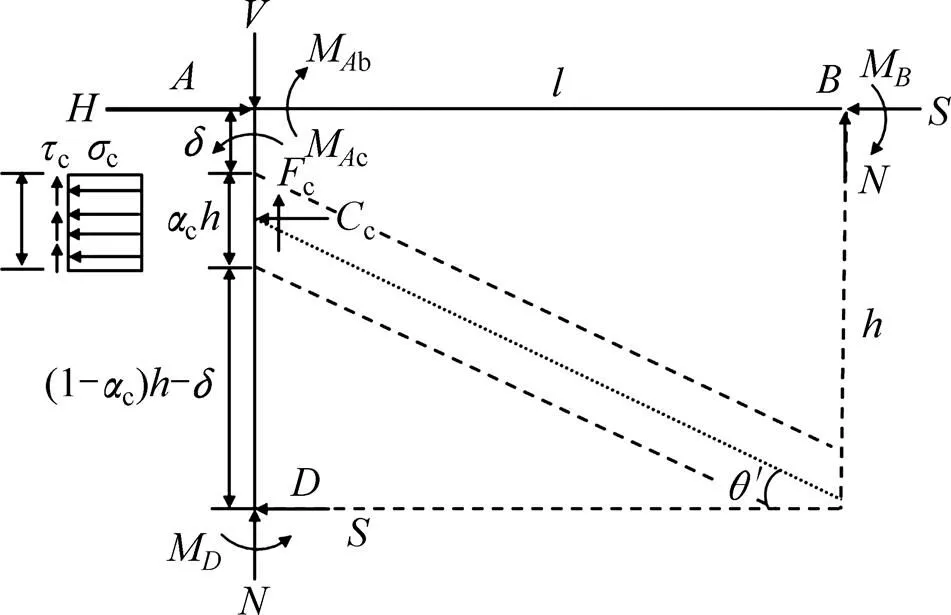
图4 框架填充墙构件在角部砖砌体被压碎后的计算简图及受力

2.2 理论公式推导

等效接触面长度指的是等效斜撑墙片与框架柱的接触长度。这里等效斜撑墙片的宽度以等效接触面长度的形式给出。在极限水平承载力作用下，等效斜撑墙片在与框架柱接触面处受剪、受压综合作用而导致破坏。根据特雷斯卡(Tresca)六棱柱体屈服准则[14]得：

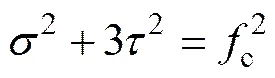
(4)

式中：为填充墙等效斜撑墙片与框架柱之间均布正应力；为填充墙等效斜撑墙片与框架柱之间均布剪应力；为框架梁柱的高跨比，即=′/′；为等效斜撑填充墙与框架柱之间的摩擦因数，一般取0.45[16]。联立式(3)和式(4)，得出接触面均布正应力为

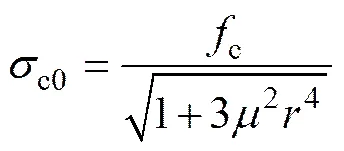
式中：c0为填充墙与框架柱之间名义均布正应力，c为填充墙材料的有效抗压强度，可按计算；为填充墙材料的抗压强度；为调整系数，可取[16]。

图5所示为框架填充墙受力变形图。由图5可见：在水平荷载作用下，假设等效斜撑填充墙片与框架柱分离的点为，为简化分析，在接触长度范围内均布剪应力忽略不计，将柱段单独提取出来作为分离体进行受力分析，根据弯矩平衡得

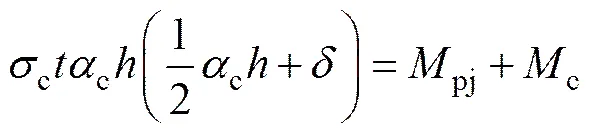
式中：c为框架柱弹性弯矩；pj为节点塑性抵抗弯矩，取节点处框架梁、柱的屈服弯矩及节点屈服弯矩的最小值。将式(2)代入式(6)，并结合式(1)，求解出等效接触面长度c为

(7)

通过以上的推导，将等效斜撑墙片宽度以斜撑墙片与框架柱接触长度c的形式给出。当1个框架填充墙构件的尺寸、材料等级确定之后，除之外的其余参数就都已经确定。即等效斜撑墙片自梁柱节点处下移的距离，不仅是等效斜撑墙片宽度计算公式的必要参数之一，也是将实体单元模型简化为单杆斜撑模型，从而可以应用于整体结构大规模的分析计算的关键。以下介绍经验计算公式的确定过程和简化模型的建模方法。

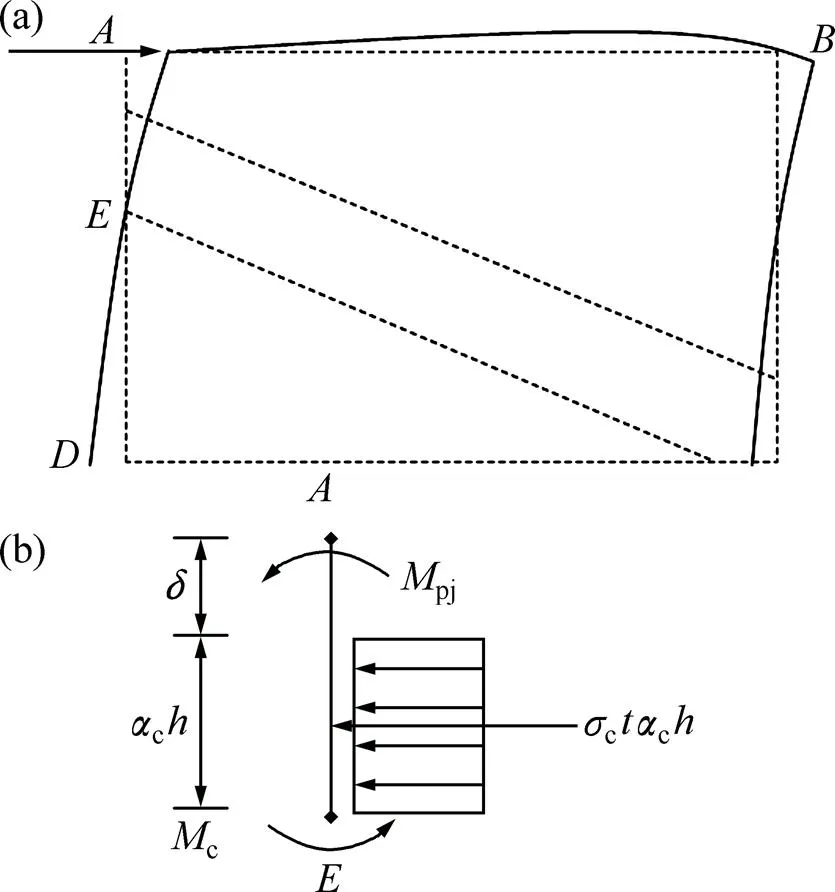
(a) 整体框架变形示意图；(b) 柱EA段受力分析图

3 斜撑杆与框架柱的接触位置

3.1 构件设计

设计一系列层高′和跨度′不同，跨高比相同的框架填充墙构件。其中框架梁、柱的截面尺寸和配筋相同，框架柱截面尺寸(长×宽)为350 mm×350 mm，框架梁截面尺寸(长×宽)为500 mm×250 mm，混凝土强度等级取C30，保护层厚度取35 mm，纵向受力钢筋采用直径为16 mm的HRB335钢筋，箍筋采用直径为8 mm的HPB235钢筋，填充墙砌体强度等级为MU10/M5，填充墙厚度取120 mm，框架的抗震等级为3级，设计轴压比取0.2，跨高比均为1.5。具体设计参数见表1。

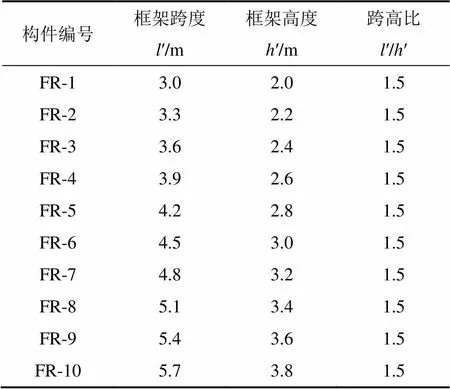
表1 构件设计参数

3.2的确定

首先采用实体单元模型的建模方法，在ABAQUS中对表1中的各个构件进行模拟计算。然后在实体单元有限元模型的基础上，采用桁架单元T3D2，将实体单元的填充墙替换为等效斜撑杆。杆两端与框架之间采用join连接，即节点之间允许有相对转角，但不允许有相对位移，对应于框架梁柱和填充墙之间只传递剪力，不传递弯矩的情况；材料属性与填充墙使用的砌体本构关系一样，在设置材料属性时规定只承受压力不能承受拉力。简化模型情况如图6所示。

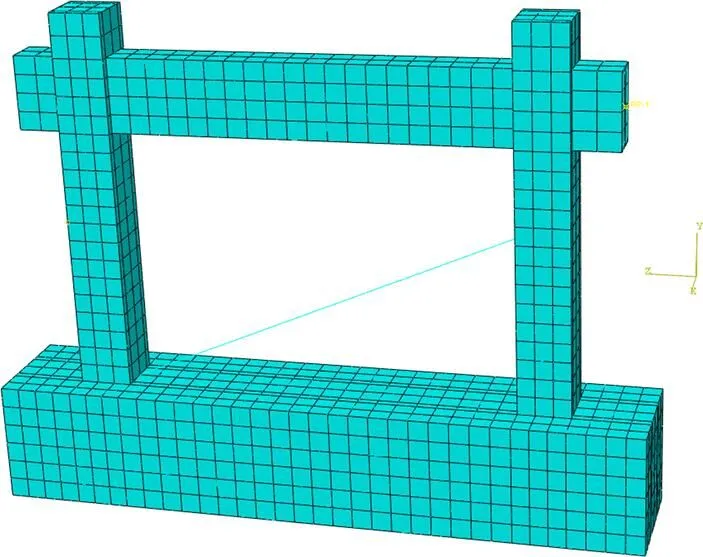
图6 等效单杆斜撑模型

逐渐调整的取值即变化等效斜撑墙片与框架柱的接触位置，直至等效单杆斜撑模型的荷载−位移曲线与实体单元有限元模型的荷载−位移曲线相吻合，记录此时的，认为此时的值即为该构件的合理取值。各个构件框架梁和框架柱的屈服弯矩按下式计算：

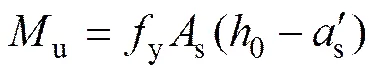
(9)

从图7可以看出：当3=350 mm时，简化斜撑模型与实体单元模型计算的荷载−位移曲线在平台段最为符合，因此认为对于构件FR-1，的合理取值为350 mm。按照上述方法，对其余9个构件采用同样的分析过程，找出当等效单杆斜撑模型的荷载−位移曲线的水平承载力最大值与实体单元有限元模型的计算结果相符时的取值。

3.3 经验公式拟合

通过式(7)的推导看出, 等效压杆的有效宽度可以通过含的表达式来表示，两者之间成正比例关系。有研究认为，等效压杆的有效宽度与′cos′和′有关[17]。再结合观察有限元实体单元模型的分析结果，本文认为与′cos′有关，/′cos′可以写成含有′的函数表达式。其中，为相对刚度参数，是由SMITH等[6]提出的，其计算公式为

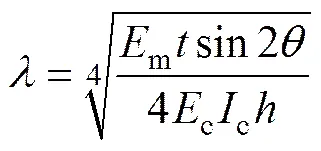
式中：m为填充墙材料的弹性模量；c为混凝土的弹性模量；为填充墙厚度；为填充墙对角线与水平方向的夹角；c为框架柱的截面惯性矩；为填充墙的高度。

本文认为/(′cos′)和′之间存在函数关系，分别计算上述设计的10个构件中当取合适的值时对应的/(′cos′)和′，将/(′cos′)作为纵坐标，′作为横坐标，并放在同一直角坐标系下，得到一系列的分布点，如图8所示。

对以上这些分布点拟合曲线得到的经验计算式为

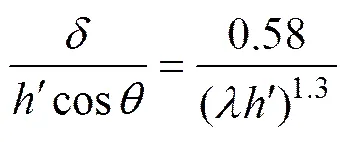
通过式(11)可以计算，即等效斜撑墙片自框架梁柱节点下移的距离。当1个框架填充墙构件的截面尺寸和材料等级确定后，可通过式(11)和式(7)计算出等效斜撑杆与框架柱的接触位置和等效斜撑墙片的宽度，即可建立对应的等效简化有限元模型。

1—实体单元模型；2—斜撑墙片下降1=150 mm；3—斜撑墙片下降2=250 mm；4—斜撑墙片下降3=350 mm；5—斜撑墙片下降4=450 mm；6—斜撑墙片下降5=550 mm。

图7 构件FR-1荷载−位移曲线

Fig. 7 Load−displacement curve of member FR-1

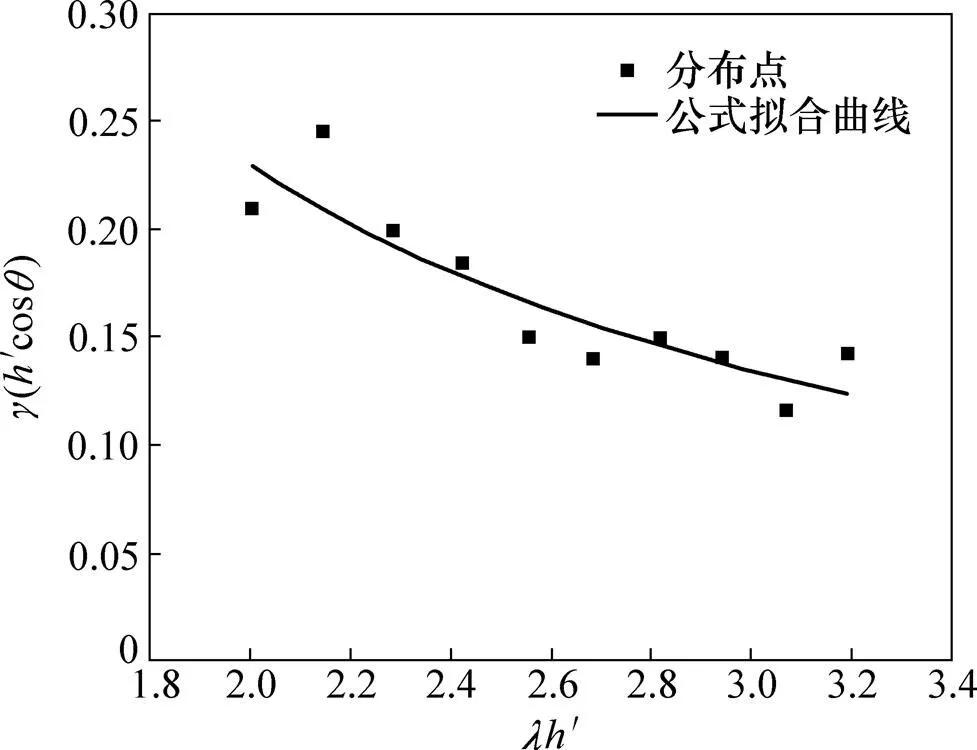
图8 分布点和公式拟合曲线

4 实例应用

4.1 试验及相关数据

Shine和Mehrabi为研究填充墙对框架性能的影响，进行了一系列共12个框架填充墙构件的拟静力试验。本文对其中的构件8和构件9进行模拟验证。构件8的填充墙为混凝土空心砌块，构件9的填充墙为实心砖砌体，构件尺寸、材料参数和实验情况详见文献[11]。

4.2 有限元计算与实验结果对比

对以上2个构件，分别采用实体单元接触连接模型、本文提出的改进的等效简化斜撑模型和传统的对角斜撑模型进行有限元模拟。其中，传统的对角斜撑简化模型的等效墙片宽度的取值采用TUCKER[8]提出的计算公式：

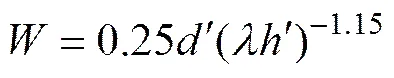
式中：为等效斜撑的宽度；′为填充墙对角线的长度；′为框架的高度；为相对刚度参数。TUCKER[8]提出的等效斜撑宽度的计算公式在对角斜撑模型中应用最为广泛，具有较普遍的意义[18]。构件8、构件9的3种有限元建模方法计算结果与实验结果的比较见图9。

从图9可以看出：采用本文所述的简化建模方法所得到的框架填充墙构件的最大水平承载力与试验所得数据和采用实体单元接触连接模型的计算结果三者之间比较吻合，验证了该等效简化模型的合理性和准确性。对于传统的对角斜撑模型，始终保持在对角线方向上的对角斜撑模型不尽合理，等效墙片宽度采用TUCKER[8]公式所得的最大水平承载力低于上述3种结果，说明该对角斜撑模型低估了框架填充墙构件的最大水平承载力，与构件的实际受力误差较大。

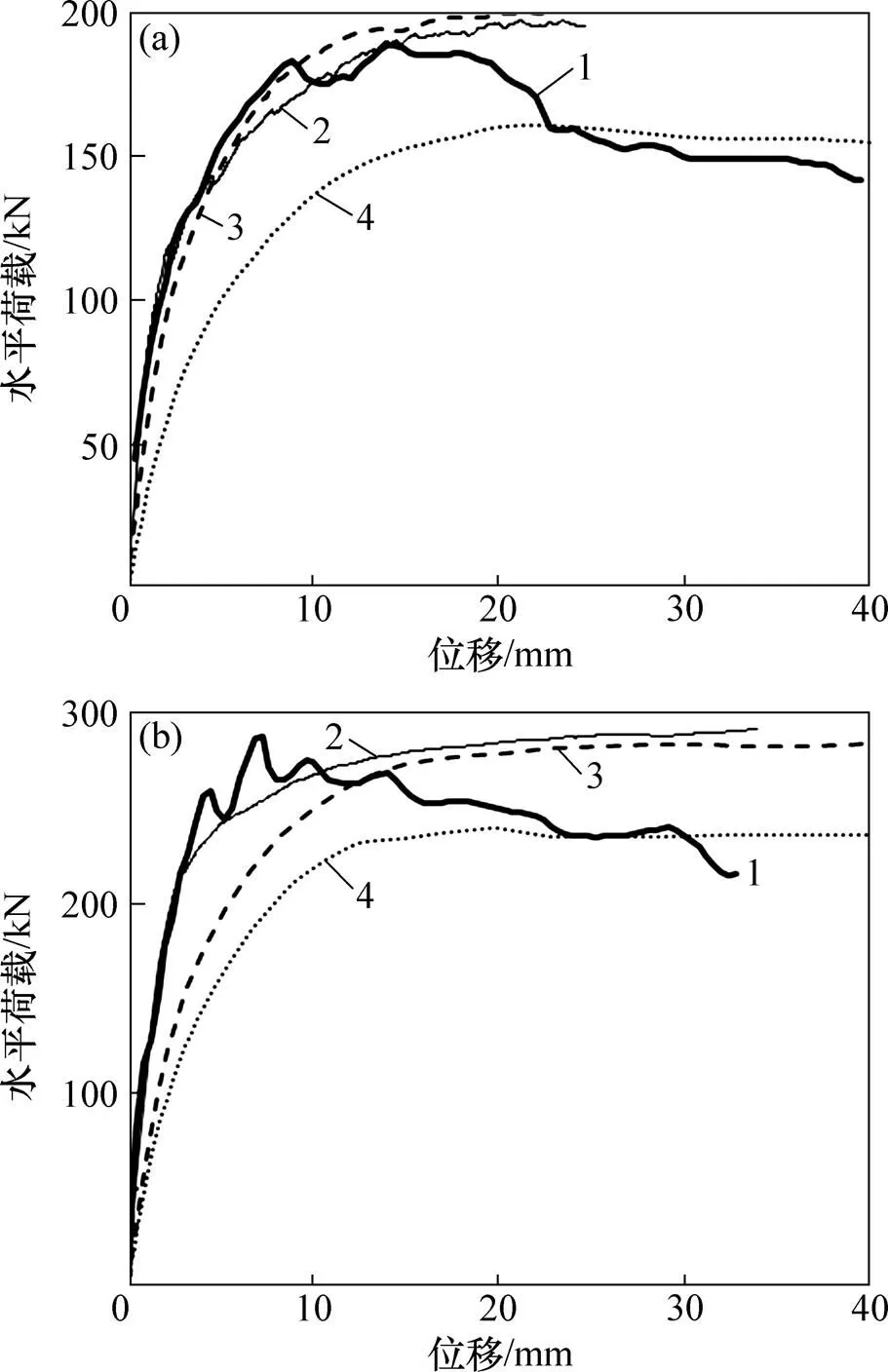
(a) 构件8；(b) 构件9

5 结论

1) 在等效对角斜撑杆模型的基础上，结合震害实例中填充墙顶部与框架梁柱节点接触处的砖砌体在大震作用下通常会被压碎的情况，将等效斜撑杆与框架柱的接触位置下移一定的距离，提出一种新的简化计算模型。在该模型的基础上进行受力分析和理论公式推导，给出了等效斜撑墙片宽度的计算公式。等效斜撑杆与框架柱接触位置的经验计算公式则是通过设计一系列框架填充墙构件进行有限元模拟，并对结果进行统计回归的方法得到。由此可以建立一种改进的等效单杆斜撑简化模型，与震害实际更相符。

2) 实体单元模型可以很好的模拟框架填充墙构件的受力情况，但计算单元多，计算时间长且不容易收敛。按本文所介绍的等效简化模型的数值模拟结果与实体单元模型计算结果和实验所得实测数据三者之间吻合得很好，采用等效简化模型不仅大大节省了计算成本，同时也使得带填充墙的框架结构整体模型的大规模时程分析计算成为可能。

3) 该简化计算模型存在一定的局限性，即只适用于在大震作用下，填充墙角部砖砌体被压碎这一破坏模式的模拟计算。在弹性阶段，填充墙与框架梁柱之间的传力方向是按对角线方向传递的，此时采用已有的对角斜撑模型即可。只有在构件进入非线性后，框架填充墙构件才会普遍出现填充墙与框架柱接触处最大应力区域下移的情况。对于处于高烈度区、严重破坏且符合本文所述的破坏模式的框架填充墙结构，采用本文所介绍的简化有限元模型进行分析更符合震害实际，模拟结果也更准确。

[1] 叶列平, 曲哲, 马千里, 等. 从汶川地震框架结构震害谈“强柱弱梁”屈服机制的实现[J]. 建筑结构, 2008, 38(11): 52−67. YE Lieping, QU Zhe, MA Qianli, et al. Study on ensuring the strong column−weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake[J]. Building Structure, 2008, 38(11): 52−67.

[2] POLYAJCOV S V. On the interactions between masonry filler walls and enclosing frame when loaded in the plane of the wall[J]. Translations in Earthquake Engineering Research Institute, 1956, 32(2): 1−25.

[3] 金焕.填充墙RC框架结构地震破坏机理及关键抗震措施研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2014: 35−47. JIN Huan. Research on seismic failure mechanisms and key aseismic measures for masonry-infilled RC frame structures[D]. Harbin: Institute of Engineering Mechanics, 2014: 35−47.

[4] SUN Baitao, YAN Peilei, CHEN Xiangzhao. New characteristics of intensity assessment of Sichuan Lushan“4.20”Ms7.0 earthquake[J]. Earthquake Engineering and Engineering Vibration, 2014, S1(13): 123−139.

[5] HOLMES M. Combined loading on infilled frames[J]. Proceedings of the Institution of Civil Engineers, 1963, 25(5): 31−38.

[6] SMITH B S, CARTER C. A method of analysis for infilled frames[J]. Proceedings Institution of Civil Engineers, 1969, 44(1): 31−48.

[7] SANEINEJAD A, HOBBS B. Inelastic design of infilled frames[J]. Journal of Structural Engineering, 1995, 121(4): 634−650.

[8] TUCKER C J. Predicting the in-plane capacity of masonry infilled frames[D]. USA: The University of Tennessee. College of Civil Engineering, 2007: 57−69.

[9] 孙柏涛, 阎培雷, 王明振, 等. 四川省芦山“4.20”7.0级强烈地震建筑物震害图集[M]. 北京: 地震出版社, 2014: 11−13. SUN Baitao, YAN Peilei, WANG Mingzhen, et al. Earthquake damage atlas of Sichuan Lushan“4.20”Ms7.0 earthquake[M]. Beijing: Earthquake Publishing House, 2014: 11−13.

[10] KOUTROMANOS I, STAVRIDIS A, SHING P B, et al. Numerical modeling of masonry-infilled RC frames subjected to seismic loads[J]. Computers and Structures, 2011, 89(1): 1026−1037.

[11] MEHRABI A B, SHING P B, SCHULLER M P, et al. Experimental evaluation of masonry-infilled RC frames[J]. Journal of Structural Engineering, 1996, 122(3): 228−237.

[12] GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010, Code for design of concrete structures[S].

[13] 刘桂秋. 砌体结构基本受力性能的研究[D]. 长沙: 湖南大学土木工程学院, 2005: 21−25. LIU Guiqiu. The research on the basic mechanical behavior of masonry structure[D]. Changsha: Hunan University. College of Civil Engineering, 2005: 21−25.

[14] ACI 318M—05, Building code requirements for structural concrete[S].

[15] CHEN W F. Plasticity in reinforced concrete[M]. New York：McGraw-Hill Book Co, 1982: 29−38.

[16] ACI530—02, Building code requirements for masonry structures[S].

[17] 金晓飞, 高松召, 杨晓杰, 等. 内嵌墙板钢框架等效单斜撑简化模型[J]. 哈尔滨工业大学学报, 2013, 45(6): 16−21. JIN Xiaofei, GAO Songzhao, YANG Xiaojie, et al. Equivalent single strut simplified model for steel frames with embedded retaining wall[J]. Journal of Harbin institute of technology, 2013, 45(6): 16−21.

[18] 阎红霞. 楼板和填充墙对RC框架结构抗震性能的影响[D]. 北京: 北京交通大学, 2012: 121−133. YAN Hongxia. Influences of slabs and infill walls on seismic performance of reinforced concrete frame structures[D]. Beijing: Beijin Jiaotong University, 2012: 121−133.

(编辑 陈爱华)

Equivalent diagonal bracing model of a frame-filled wall

DENG Hongyu1, SUN Baitao1, 2

(1. College of Space Technology and Civil Engineering, Harbin Engineering University, Harbin 150001, China;2. Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China;3. School of Water Conservancy and Civil Engineering, Northeast Agricultural University, Harbin 150030, China)

Based on the existing equivalent diagonal strut model, combined with the actual earthquake damage phenomena that the brick masonry between the top of the infill wall and the beam-column connections is often crushed during a strong earthquake, and changing the contact position between the equivalent bracing wall and column, a new calculation model was generated. Through theoretical derivation, the formulae for calculating the contact length between the equivalent bracing wall and column was given. Using the ABAQUS finite element simulation, an empirical formula for the reasonable contact position between the equivalent bracing wall and column was determined. Finally through comparing the finite element model calculation results with the experimental result, the validity of the simplified modeling method was verified. The results show that the traditional diagonal strut model underestimates the horizontal bearing capacity of the infill-frame, and the new model is more consistent with the seismic damage of frame structure in Lushan earthquake. The model has reference significance to seismic analysis of frame structure.

masonry infill panel; reinforced concrete frame structure; equivalent strut mode; shear strength; stiffness

10.11817/j.issn.1672−7207.2017.02.023

TU31

A

1672−7207(2017)02−0440−08

2016−03−15；

2016−06−10

国家自然科学基金资助项目(91315301)；地震行业科研专项(201508026-01，201508010-06)(Project(91315301) supported by the National Natural Science Foundation of China; Projects(201508026-01, 201508010-06) supported by Earthquake Industry Research)

邓宏宇，博士，讲师，从事结构抗震研究；E-mail：dengblue@163.com