跳棋系统中的关键算法
张阳+黎素珍

摘要:计算机博弈是当下在人工智能范畴内一个十分重要并且十分有挑战性的课题,是人工智能领域的重要分支。人工智能在棋类游戏中的应用十分广泛。目前,对于五子棋,国际象棋,中国象棋等棋牌类游戏的计算机博弈软件有很多且智能水平都相对较高,而高水平跳棋软件在国内并不多见。该文在对大量相关文献的分析和研究的基础上,具体研究了跳棋博弈软件的博弈树搜索算法、评估函数。提出了三种不同搜索效率的算法来实现分级博弈,评估算法使用TD-BP算法。论文主要研究了以下几个方面的问题:第一,根据走法生成所构造的博弈树,研究了一些广泛使用的博弈树搜索算法,并介绍了一些改进的搜索算法,在设计中结合部分搜索算法进行使用。第二,研究了主要包括静态估值函数和其他具有机器自学习能力的评估函数,在实际设计中,将BP神经网络与增强学习算法结合使用。
关键词:计算机博弈;搜索算法;分级博弈;评估函数
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2016)33-0070-04
1机器博弈系统关键要素
机器博弈系统的设计是将现实中的棋牌类游戏通过计算机语言表达,并通过计算机强大的存储能力和计算能力使计算机拥有较高的棋力水平。
在机器博弈中,最核心的思想就是对博弈树节点的评估函数和对博弈树搜索方法的结合使用。
机器博弈的基本思想确定一个机器博弈系统的基本构成如下:
1) 知识表示,可以用来描述当前棋局中各个棋位上的落子情况,各棋子之间的关系及棋子与某棋位之间关系等信息。博弈系统可以从中读取当前棋局的状态信息,知识表示往往是机器博弈系统值非常基础但是不可或缺的一部分。
2) 走法产生机制,主要在某一棋局状态下用来产生整个博弈树,即在当前棋局下,生成走棋方可选择的所有走棋方案。在博弈树的任意一个节点上,走法产生机制可以产生这个节点的所有子节点,各子节点再产生孙节点,通过逐层生成,最后生成完整的博弈树。
3) 搜索算法,主要用来在博弈树中的所有合法走法中选出一个利益最大的走法,即最优路径。
4) 评估函数,根据某一棋局的具体特征对当前棋局进行评估并量化,为搜索算法的选择提供依据,从而通过搜索算法找出最优走法。
2 跳棋软件搜索算法的设计
2.1跳棋博弈系统的搜索算法与分级博弈
本文主要对跳棋系统的分级博弈进行设计与实现。分级博弈的控制有两种设计方式:
1)使用不同的搜索函数,通过搜索效率与搜索的准确度的差别来区分博弈等级。
2) 使用相同的搜索函数,并通过不同准确度的评估函数来区分搜索函数的准确度,从而实现分级博弈。
本文主要研究设计使用不同的搜索函数来实现不同级别的人机博弈。
由于在跳棋游戏中博弈树的深度不可估计,所以在搜索时深度要达到博弈树的最终深度基本是不可能的,而且跳棋系统在实际使用时,要考虑到网络延迟,服务器的负载能力等因素,为了不影响用户的游戏体验,所以在设计搜索函数时,设定一个搜索时间上限t,使用迭代加深的搜索算法,在t时间内,各个博弈级别的搜索函数将当前所能搜索到的最优解作为最终方案。根据服务器不同的性能设置不同的搜索时间上限t。
根据本章上述小结对各种博弈树搜索算法的优劣分析与比较,本文设计了三种博弈树搜索算法。三种搜索算法如下:
1)负极大值与迭代加深相结合算法,使用该算法来实现初级博弈水平的博弈树搜索,该算法的部分伪代码如下所示:
在该算法中,虽然使用了迭代加深搜索算法来控制搜索的深度,但是在某一深度搜索时,该搜索算法没有使用任何剪枝技术,造成搜索时间比较长,搜索深度不能达到理想深度。其实此算法与传统的广度优先算法相比并没有任何优势,甚至在搜索的时间复杂度上更复杂,但是考虑到实现过程中的控制方便,使用了迭代加深的搜索算法。
在初级水平的跳棋系统中,该搜索算法的搜索结果与实际最优解往往相差很大,计算机棋手的走子的水平也相对较低。
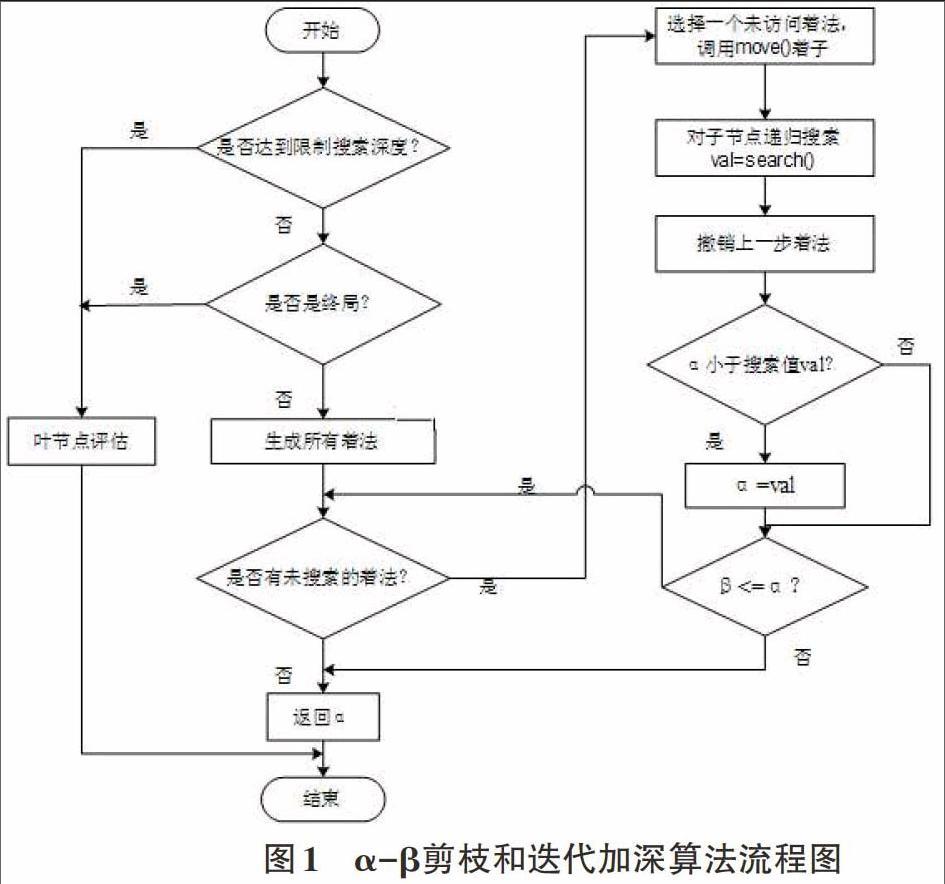
2)采用了α-β剪枝搜索算法和迭代加深算法相结合的算法作为本系统的搜索算法,该算法在初级博弈水平的搜索算法的基础上结合了迭代加深算法。在规定的搜索时间内,在深度不断增加的情况下对博弈树进行循环搜索,在搜索深度达到temp时,将该层节点进行排序,并从根节点开始深度为temp+1的搜索,在搜索过程中,从temp深度的搜索结果中已排序的最优节点开始优先搜素,进行α-β剪枝,搜索完毕后再对搜索节点再次排序,如此循环搜索,直到达到搜索时间限制或者得到最优解。该算法的流程图如图1所示。
该算法与1)中的算法相比,在搜索过程中结合了α-β剪枝的搜索方法。由于在某一深度的搜索过程中,对该深度的节点进行评估排序,在深度增加后的搜索过程中会优先搜索更优的节点,所以该算法的剪枝的效果非常好,效率也会大大提高。
该算法在2)中算法的基础上与置换表启发算法相结合,在搜索博弈树过程中,将搜索过的节点信息,包括节點评估值、深度、当前棋局状态以及最优节点信息保存在置换表中。搜索时,在某一深度搜索中,如果遇到置换表中存在相同的棋局状态,则直接在置换表中提取信息,选择最优节点进行下一深度的搜索。另外使用了渴望搜索算法替换了普通的α-β剪枝搜索算法,由于本算法使用了置换表启发,所以渴望搜索中的期望搜索值可以比较精确,所以在搜索效率上会有很大提升。
该算法与2)中算法相比,减少了迭代加深算法在各个深度搜索时对节点进行评估排序的消耗,考虑到博弈树的宽度,在数据库中搜索置换表的信息产生的消耗往往比在某一层中队所有节点进行评估排序的消耗小的多。另外,随着搜索的深度不断增加,对无用节点的搜索也会相应增多,所以使用置换表能够很好的提高搜索效率。但是,该算法比较依赖于置换表中信息的数量与准确性,所以,需要为跳棋软件提供大量学习样本进行训练,才能体现出该算法的优势。
在本节中,主要设计三种博弈树算法来实现分级博弈,通过控制搜索时间来区分搜索结果的优劣。
本文设计的三种搜索算法都使用到了迭代加深算法。从表面上看,该搜索算法在循环搜索的过程中会对浅深度的博弈树节点重复搜索。但在博弈树中,随着深度的增加,节点数呈指数倍增长,所以对浅深度节点的多次遍历造成的冗余可以忽略不计。并且在实际使用过程中,在限制的搜索时间内,对搜索深度的估算不切实际,在不同的棋局局面下搜索的深度都不相同。所以,使用迭代加深的搜索算法思想效果比较好,搜索效率并不比广度优先搜索算法慢很多,而它的空间复杂度却和深度优先搜索算法差不多,比广度优先算法小很多。
3 跳棋系统评估函数的设计
在博弈树的搜索中,因为计算机的资源有限和对机器反应的实时性有一定的要求,所以机器搜索往往不能达到很深的层次。因此可以机器搜索博弈树的过程中,搜索达到一定深度时,对当前棋局进行评估,从而机器可以根据评估值的优劣来选择具体的走法[1]。
棋局评估就是对当前局面状态信息进行量化成计算机能够识别的机器语言,计算机利用量化信息对当前局面进行推理、判断及评估,评估出当前局面的优劣,进而做出行动决策。对于一个具体的博弈对象来说,局面评估是影响机器求解是否准确的关键[2]。
3.1静态估值方法
静态估值算法是指对于任何一个棋局状态,根据人类对该棋类的了解,选取出对当前棋局状态优劣有影响的几个因素,并根据这几个因素对棋局的影响力大小,给它们分配对应的权值,以下是静态估值方法的形式化公式:
设y是最终要得到的评估值,xi为影响棋局优劣的各个因素,wi为对应的特征xi对棋局影响力的权值。
在静态估值函数中,决定静态估值函数的主要有四个因素:
棋子价值的评估:在一些棋类中,因为各棋子存在走法限制,所以棋子的种类的不同决定了该棋子的价值,比如在象棋中,车和马的价值就不同,在跳棋游戏中,因为各个棋子在走法上不存在什么差异,所以初始的价值都是相同的。
棋子在棋盘中位置的评估:几乎在所有棋类中,棋子在棋盘中的位置不同,棋子相应的价值也会不一样。比如在跳棋中,处于敌方阵营的棋子的价值最大,距离地方阵营越近的棋子其价值也越大。
棋子灵活性的评估:棋子的灵活性主要体现在该棋子可以有多少种走法,每一种走法也都有相应的价值。
棋子位置关系评估:棋子之间的关系是评估算法中非常重要的一个因素,在博弈时,己方的一个棋子可能对对方造成威胁,也有可能对对方形成帮助。在跳棋博弈中,如果一个棋子可以被对方某棋子当做跳的桥,则该棋子的价值应该降低,而若该棋子可以被己方其他棋子当做跳棋的桥,则该棋子的价值应该增加。若该棋子占据了对方棋子要跳棋的落点位置,则该棋子的价值也应该得到增加,相反,若占据了己方其他棋子跳桥的落点位置,则该棋子的价值应该得到削减。
但是任何一种棋类棋局的评估的要素往往错综复杂,人为基本上不可能考虑完全并对应每个特征并给出合理的权值,肯定会有所误差。然而由于在大部分搜索算法中,博弈树搜索的过程是先搜索到某一深度,根据其评估值,再由下向上回推到根節点,从而得出搜索的结果路径,所以如果在某一层的某个节点处发生评估值误差,可能会引起上级节点处的决策误差而选择错误的分枝,通过层层向上传播到根节点,搜索算法最后将会得到一条错误的路径,而且该错误也是不能挽回的。
虽然静态估计值有上述很多缺点,但其在机器博弈的实际应用中,可以利用静态估值算法构造一个简化的机器博弈系统,该系统可以用来与具有机器学习能力的机器博弈系统对弈,为该机器博弈系统提供学习模式,从而提高其评估函数的准确性。
由上面所述可以知道,仅仅根据人对棋类知识的了解与下棋的经验来确定评估函数,不仅开销较大而且得到的评估值往往不够精确,从而会使得博弈树的搜索结果准确度降低。
3.2 TD-BP学习算法
在机器博弈的实际运用中,棋局千变万化,所以提供给机器学习的学习模式是有限而且不一定满足要求的,而且样本的输入也对系统造成了很大的负担。
增强学习(Reinforcement Learning and Control)是非监督式的学习方法,在机器博弈中运用十分广泛。增强学习不依赖于学习样本,而是在与环境的交互中进行学习[3]。增强学习的基本原理:agent在某一状态下对环境进行动作action,环境随之改变,根据环境改变是否有益,环境根据一个回报函数给以agent一个奖赏值,经过多次的与环境交互,agent从而获得一个奖赏值最高的策略。增强学习是一种与人类学习方式最为相近的学习方式,具有很高的应用研究价值。
瞬时间差分(Temporal Dierence Learning)学习是一种经典的增强学习算法,是蒙特卡洛方法和动态规划方法的融合[4]。与BP神经网络算法不同的是,瞬时间差分算法不依赖于教师信号,可以直接从经验中学习,并且可以通过与环境的交互来及时修正权值与误差。
由于BP神经网络有比较好的学习和泛化能力,可以弥补TD算法泛化能力差的缺陷。BP神经网络是有监督的学习,即对每个输入样本都要求有期望输出,输入样本和期望输出构成学习样本,但是在博弈过程,能够知道期望输出的仅仅是最后获胜棋局的前一棋局状态,而在博弈过程中的中间棋局状态无法获得期望输出,如果单纯以棋局状态与最终结果作为训练样本,这种方式是不可取的,因为博弈的中间棋局状态的变化太大,此时如果结合TD算法,可以正好弥补了应用在跳棋博弈中BP神经网络的有教师信号学习的缺陷,TD学习算法不需要通过期望输出来进行权值调整和误差修改,而是利用后面的局面状态来估计和分析当前的局面,可以对博弈过程中的任何一个棋局进行学习,把BP学习模式转换为无监督式学习。TD-BP算法主要思想是利用预测误差的方法来调整神经网络各连接的权值,通过对多个局面进行学习分析,得到更为准确的评估值,提高BP神经网络与现实的拟合度。假设观察的结果序列是X1,X2...Xm并且Z是观测到的最终结果,Xi对应某一i时刻的观测结果,对应这m个观测的结果,使用评估函数进行评估,可以得到p1,p2...pm,m个Z的估计。现假设每一个Z的估计都是关于观测结果的函数,由于BP神经网络属于有教师学习,根据上一小结所述,BP神经网络把观测结果与最终观测结果Z做比较,用标准输出来产生误差e。根据误差e,从输出方向输入方逐层修改权值,即:

