B-S和二叉树两种期权定价模型在财险定价中的应用与比较

李子耀，黄洪瑾

（安徽财经大学，安徽蚌埠233040）

一、财产保险与期权的异同

（一）财产保险与期权的相同点

第一，两者的标的物具有相似性。财产保险合同的标的物是财产，在本质上，期权合约的标的物是金融资产，从这方面来说，财产保险合约与期权合约的标的物具有相似性。

第二，两者的法律约束相似。保险合同是投保人与保险人就双方权利义务关系而签订的协议，当合约被履行或者超过合约的规定期限时，投保人与保险人之间的权利义务关系即刻解除。期权合约也是如此，期权的买方可以在期权到期之前根据实际情况选择是否行使自己的权利，权利的行使时间取决于期权合约的种类，但是若买方在期权到期之前不行使权力，期权合约便自动失效。

第三，参与双方的权利义务关系相似。在财产保险中，投保人通过支付相对较少的保费将因未来标的物遭受损害给自己带来的经济损失风险转嫁给保险人，若标的物在未来发生了特定的风险事故，投保人就会获得相应的补偿；反之，投保人则损失少量的保险费。在期权中，期权的买方通过支付期权费获得在规定期限内按照约定的价格买入或卖出一定数量资产的权利，根据实际情况，若执行期权对自己有利，买方就会行使自己的权利以获得较高的收益；反之，买方就会放弃行使权利，这样损失的也不过是少量的期权费，而可能获得的收益却是较高的。

（二）财产保险与期权的不同点

第一，两者转移的风险不同。财产保险转移的是纯粹的损失风险，而期权转移的则是市场风险。

第二，两者的执行价格不同。财产保险的执行价格取决于标的物遭受损失的程度以及保险合同中约定的赔偿上限，是不确定的；而期权的执行价格则是在双方在交易时就在期权合约中确定下来的一个固定的价格。

第三，两者的执行次数不同。财产保险中，在约定的时间与保险金额的限度内，如果特定的风险事故多次发生，则保险合同可以被执行多次；而期权合约在约定的时间内，最多只能被执行一次或者不执行。

第四，两者赔偿的执行方式不同。财产保险的投保人必须拥有相应的实物资产且必须具有保险利益时才能投保，且只有在保险事故发生时才能获得相应的赔偿；而期权的双方可以在不拥有标的资产的情况下借期权套利，到时只需要支付价差即可［1］。

二、期权定价模型应用于财险定价中的可行性分析

（一）影响期权与财产保险价格的主要因素相同

下面以美式看跌期权为例来说明期权与财产保险价格具有相同的影响因素。

第一，行权价格。对看跌期权而言，行权时的收益等于期权的行权价格减去标的资产的市场价格，所以在其他条件不变的情况下，期权的行权价格与看跌期权的价格呈正向变化。期权中的行权价格即财产保险中的保额，保额与保险费也同样呈正向变化，但是需要注意的是，财产保险中的保额最高不得超过保险标的本身的价值。

第二，合约的有效期。对于美式看跌期权而言，由于它可以在期权到期日前的任何时间执行，所以期权的有效期越长，期权买方获利的机会就越多，而买方承担的风险就越高，从而期权的价格就越高。在财产保险中也是如此，保险期限越长，承保人承担的风险越高，保险费用越高。

第三，标的资产价格的波动率。波动率是反映标的资产未来价格变动的不确定性的指标，波动率越大，则期权到期时标的资产的市场价格涨跌到对期权多头有利的可能性也就越大，期权的价格也就越高。在财产保险中，标的资产价格的波动率可以看做是保险标的所面临的风险大小，保险标的所面临的风险越大，则保险的价格越高。

（二）两者的价值函数图像相似

下面继续以看跌期权为例来说明两者具有相似的价值函数图像。

在看跌期权中，可以作出如图1所示的价值示意图。在图1中，P代表看跌期权的权利金，X代表执行价格，S为标的资产的市场价格。当S≥X时，多头处于亏损状态，且最大损失不随着S的变化而变化，恒等于权利金；当XP＜S＜X时，多头处于亏损状态，且亏损随着S的增加而增加，但最多不超过权利金；当S=X-P时，多头的损益为0；当S＜X-P时，多头处于盈利状态，且盈利随着S的减小而增加，当S趋于0时，多头盈利接近X-P。

在财产保险中，保费相当于看跌期权中的权利金P，而保险金额就相当于执行价格X，这样我们可以作出如图2所示的财产保险的价值函数图像。可以看出，看跌期权和财产保险的价值函数图像大致相同，这也为将期权定价模型运用在财产保险的定价中提供了理论依据［2］。

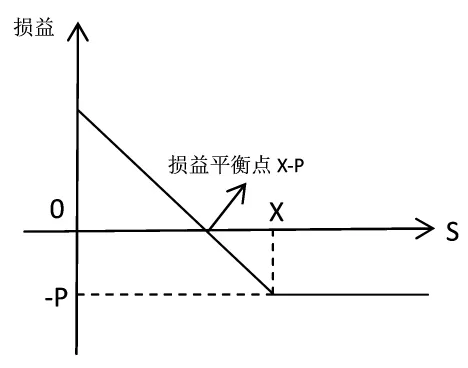
图1 看跌期权的价值图

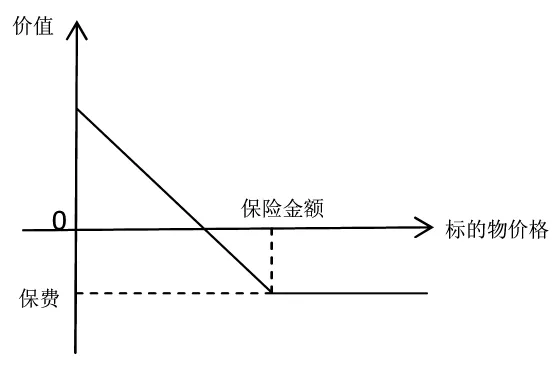
图2 财产保险的价值图

三、B-S期权定价模型与二叉树期权定价模型简述

（一）B-S期权定价模型

20世纪70年代初，布莱克（Black）和斯科尔斯（Scholes）提出了著名的布莱克斯-科尔斯期权定价模型（简称B-S期权定价模型）。后来，默顿（Merton）进一步弱化了B-S期权定价公式所依赖的假设条件，使得这一模型在现实生活中得到了进一步的推广。

B-S期权定价模型有如下基本假设：①股票价格满足随机微分方程：dS=μSdt+σSdz，其中μ和σ都为常数；②市场没有卖空限制；③无交易费用和税收，即市场是没有摩擦的；④所有证券都可以无限细分；⑤在期权有效期内，标的股票没有股利发放；⑥不存在无风险套利机会；⑦无风险利率为一已知常数；⑧期权只能在到期日执行，即此模型只适用于欧式期权。

基于上述假设，他们推导出计算期权价格的基本公式如下：

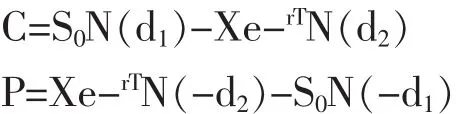
其中，

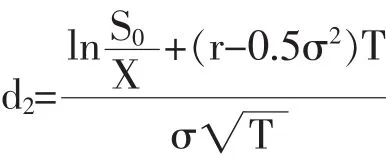
公式中，C为看涨期权的理论价格；P为看跌期权的理论价格；S0为标的资产的当前价格；N（d1）、N（d2）分别为 d1、d2的累计概率分布函数；X 为执行价格；T为期权的有效期（以年为单位）；r为无风险利率；σ为标的资产的波动率。

（二）二叉树期权定价模型

二叉树期权定价模型是由考克斯（Cox）、罗斯（Ross）和鲁宾斯坦（Rubinstein）在1979年提出的一种经典的期权定价的数值方法，与B-S期权定价模型相比，它较为直观简单，不需要太多的数学知识就可以应用。

二叉树模型的基本思想是利用离散的模型来模拟资产价格的连续运动，然后利用均值和方差匹配来确定相关参数，最后从二叉树图的末端一直往回倒推求出当前期权的合理价格。

基于这一思想，他们推导出期权价格的计算公式为：

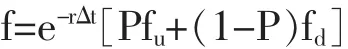
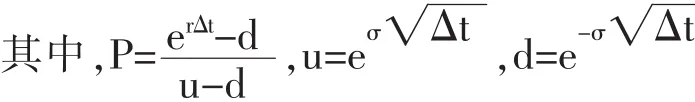
公式中，f为期权的价格；fu为标的资产价格上升时期权的回报；fd为标的资产价格下降时期权的回报；P为标的资产上升的概率；r为无风险利率；Δt为以年为单位的二叉树每期的时间间隔；σ为标的资产的波动率。

四、B-S模型和二叉树模型在财险定价中的实证分析

下面以某保险公司的家庭财产综合险为例，分别利用B-S期权定价模型和二叉树模型进行保费的仿真计算。

在这里，我们假设标的资产的可能价格为5万元、10万元、15万元、20万元；免赔率为 5‰、10‰、20‰、30‰；资产波动率为 3%、5%、7%；到期时间为 1年；选用2016年记账式附息（一期）国债的年利率2.32%为无风险利率。

将上述假设的数据分别代入B-S期权定价公式，我们可以计算出不同情况下的价格，如表1至表4所示。

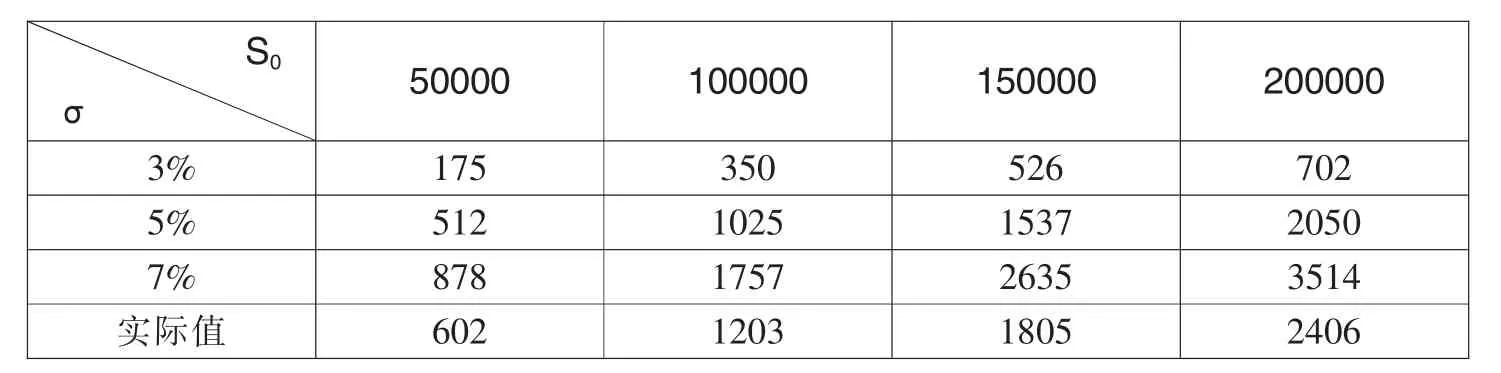
表1 B-S模型计算出的免赔率为5‰时的价格表 单位：（元）

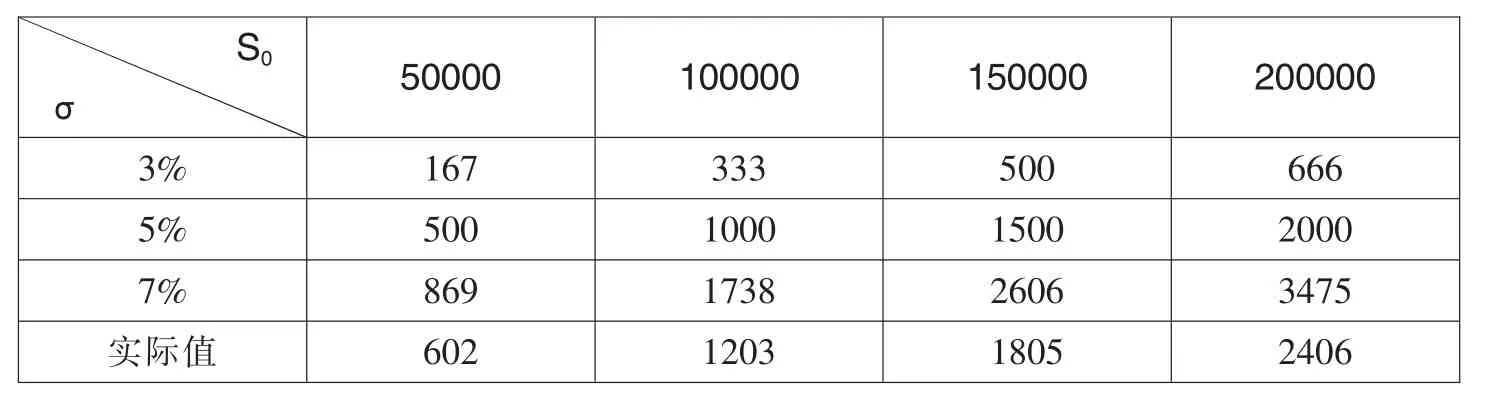
表2 B-S模型计算出的免赔率为10‰时的价格表 单位：（元）

表3 B-S模型计算出的免赔率为20‰时的价格表 单位：（元）

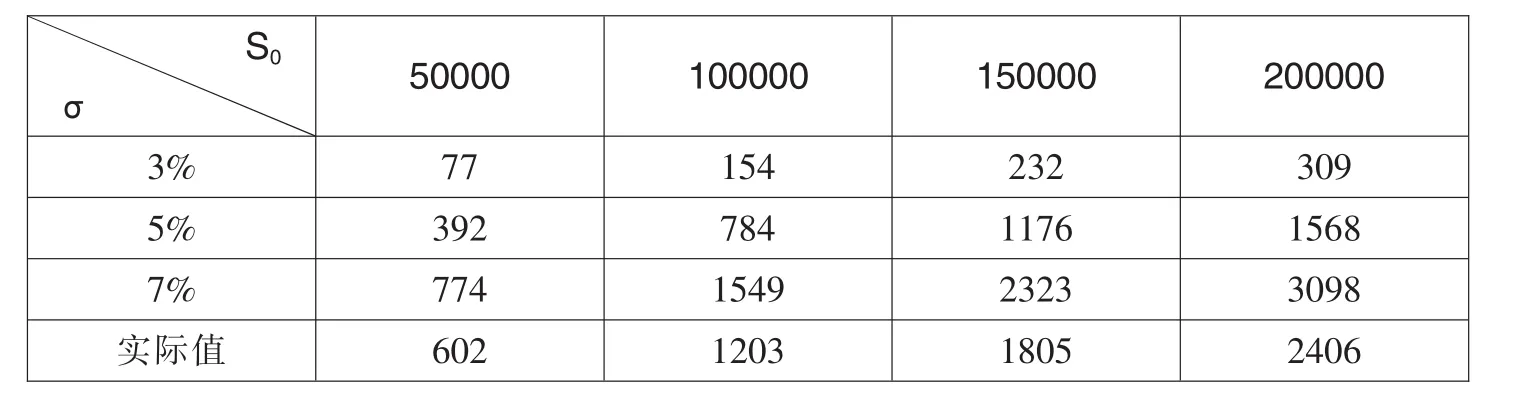
表4 B-S模型计算出的免赔率为30‰时的价格表 单位：（元）

同理，我们可以利用二叉树模型计算出不同情况下的价格如表5至表8所示。

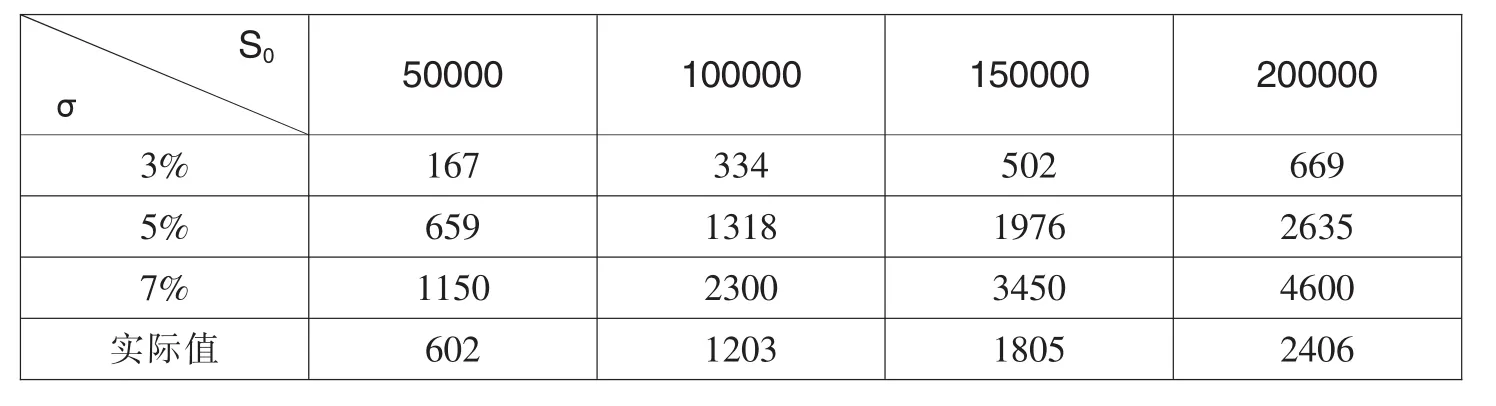
表5 二叉树模型计算出的免赔率为5‰时的价格表 单位：（元）

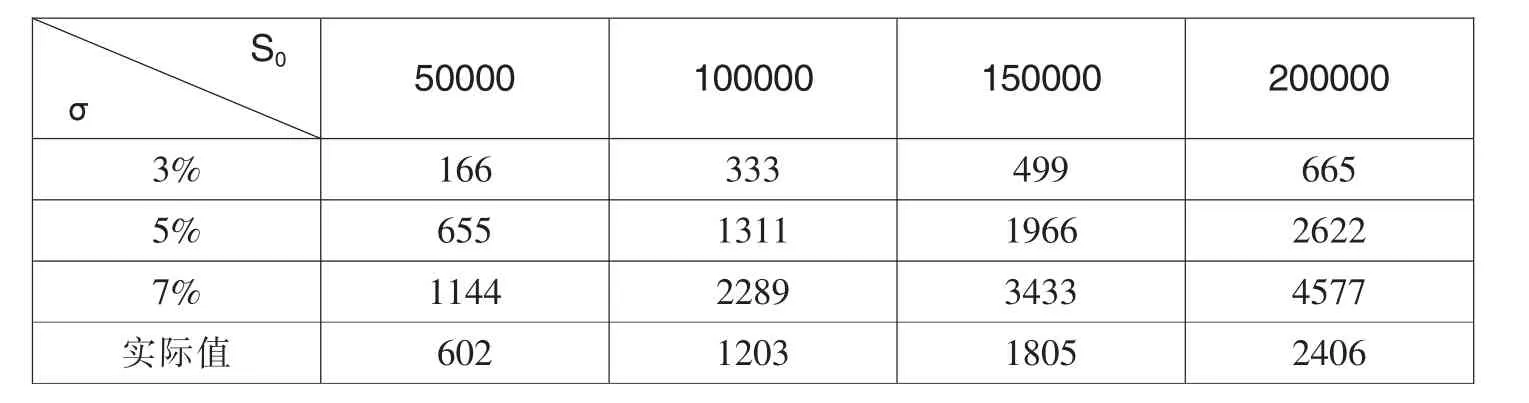
表6 二叉树模型计算出的免赔率为10‰时的价格表 单位：（元）

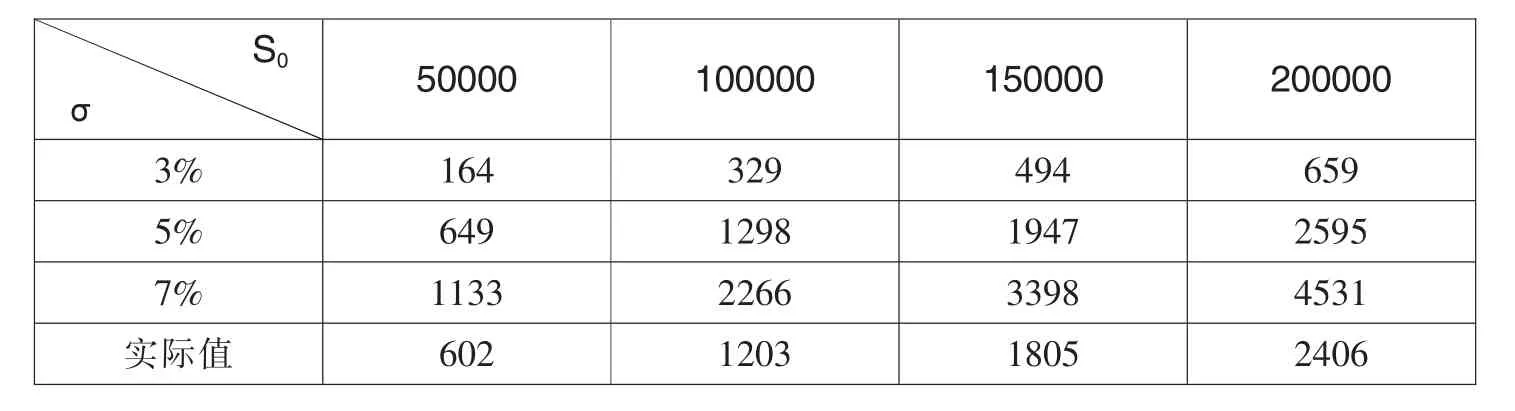
表7 二叉树模型计算出的免赔率为20‰时的价格表 单位：（元）

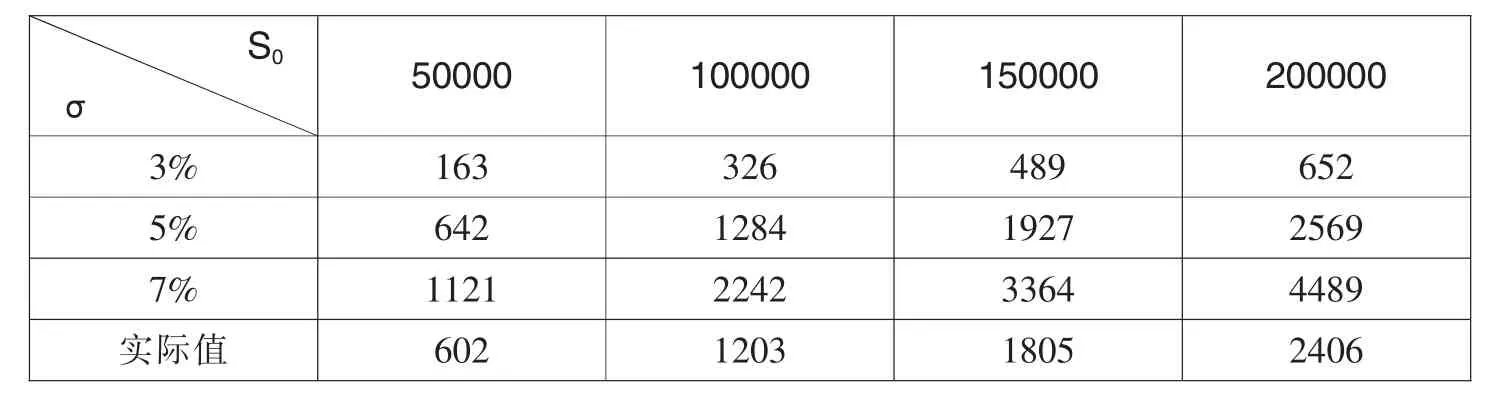
表8 二叉树模型计算出的免赔率为30‰时的价格表 单位：（元）

为了更加直观地比较B-S模型计算出的理论价格、二叉树模型计算出的理论价格与真实值之间的关系，我们把上述计算出的数据绘成如图3至图6的折线图，图中横坐标表示标的资产价值，纵坐标表示计算出的保费，不同的资产波动率已在图中标出。

图3 免赔率为5‰时的价格图

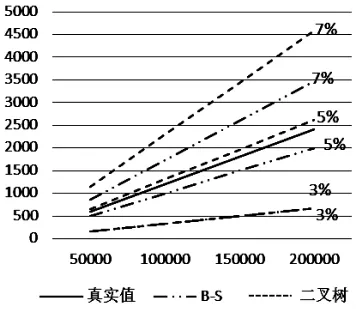
图4 免赔率为10‰时的价格图

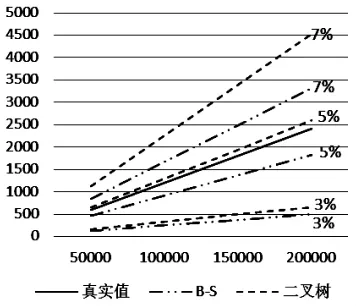
图5 免赔率为20‰时的价格图

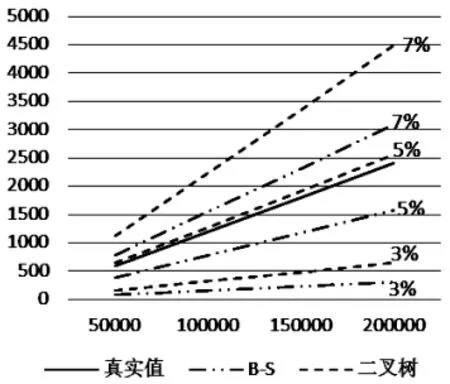
图6 免赔率为30‰时的价格图

从图3至图6中我们可以得出以下结论：①利用这两种模型计算出的理论价格与真实价格的变化趋势相一致，且两者之间有着比较明显的线性关系，这说明两者的拟合性较好；②资产波动率为5%时两种模型计算出的理论价格更接近真实值；③在其他条件不变的情况下，随着免赔率的增加，B-S模型中资产波动率为7%的理论价格越来越接近真实值，资产波动率为5%和3%的理论价格与真实值逐渐偏离；而在二叉树模型中，随着免赔率的增加，资产波动率为7%和5%的理论价格越来越接近真实值，特别是在资产波动率为5%的情况下，理论价格与真实值十分接近；④标的资产价格较低时，理论价格与真实值的差值较小，随着标的资产的价格增加，两者的差值逐渐变大。

五、两种期权定价模型的比较

第一，从这两种期权定价方法的求解角度看，B-S期权定价模型属于解析法，而二叉树期权定价模型属于数值法。B-S期权定价模型在期权的交易策略中给出了较为清晰的定量分析，得到了一个确定的解析解，在期权的数量较少时，利用B-S期权定价模型较为方便［3］。但是B-S模型在很多情况下无法得到期权价值的解析解，这个时候就要用到数值方法，但二叉树模型的计算量大且效率较低，从这一点上看，利用B-S模型进行财产保险的定价较为简便。

第二，从应用的方面来看，二叉树定价模型的应用范围较广。B-S模型只适用于期权到期执行的情况，即只能为欧式期权定价而不能应用在美式期权上，而二叉树模型是基于标的资产在一段时间内的变化而不是一个时间点上的价格，所以二叉树模型可以用在任意时间行权的美式期权的定价上以及可在一系列特定时间行权的百慕大期权的定价上。由于保险索赔发生的时间不确定，所以从这方面来看，应用二叉树模型较为符合财产保险的特点。

第三，和B-S模型相比，二叉树模型的透明度较高且能够根据实际情况快速作出调整。在二叉树图中我们可以清楚地看到每一步的结果，并且可以很容易地理解这种定价思想，而在B-S模型中则很难看到标的物价格和期权价值的变化［4］。

六、结 论

通过以上实证分析可知，将期权定价模型运用在财产保险的定价中是科学合理的，由于这两种期权定价模型各有其优缺点，所以在实际应用中我们可以根据不同情况选用不同的方法，也可以将这两种模型结合运用使得计算出的保费更加合理。将这两种模型运用在财险的定价中也有着不可避免的缺陷，比如无法将管理成本、佣金等影响保费的因素体现在公式中等，但是这种方法仍可以为财产保险的定价提供一些新思路。

［1］朱良成.简评期权定价思维和保险精算思维的相互关系［J］.新经济，2014（Z1）：11-12.

［2］张骋.期权定价在保险中的适用性探讨［J］.中国证券期货，2011（8）：29-30.

［3］万换林.期权定价理论及方法探析［J］.延安大学学报（自然科学版），2012（2）：28-32.

［4］于德胜，张晓娇.浅谈实物期权两种定价模型的比较［J］.现代经济信息，2011（13）：211-212.