Gompertz模型在大坝沉降安全监测中的应用

王开拓，辛全才，蔡生如

(1.青海民族大学建筑工程学院，青海 西宁 810007;2.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100;3.青海引大济湟水电建设有限公司，青海 西宁 810000)

0 引言

在大坝的安全监测工作中经常要对大坝的各种监测量进行预测，预测的准确性对大坝的安全评估起着重要作用［1］。在各种预测项目中，大坝的沉降与不均匀沉降产生的裂缝严重影响着坝体的安全运行，因此，沉降量是大坝的主要监测、控制项目，也是评价大坝安全和坝体质量的主要指标［2］。目前常用的大坝沉降预测模型有指数模型、双曲线模型、灰色理论 GM(1，1)模型、Verhulst模型［3］、遗传算法和神经网络法［4］等，每种方法都有其优缺点，其中指数模型和双曲线模型的应用较为简单，方便工程师掌握，但这两种模型并不能较好地模拟大坝的整个沉降过程，灰色理论GM(1，1)模型在后期预测时误差一般较大，遗传算法和神经网络应用复杂，一般工程师难以掌握。本工程采用Gompertz模型来预测大坝的沉降量，分析其准确性，该模型具有形式简单、使用方便的特点。

1 Gompertz模型与坝体沉降

1.1 Gompertz模型

Gompertz(龚帕兹)模型是由英国统计学家与数学家B.Gompertz提出的，具有3个参数，呈S形，早期主要用于模拟植物的生长高度，后来在生物学、经济学、统计学和工程学等领域内应用广泛，其基本数学表达式为

式中，a、b、c为参数;t为时间序列;y为对应不同时间t的数据预测值。

Gompertz模型具有3个典型阶段，以植物生长为例，在初期阶段，植物生长缓慢，速率较小;待植物生长到一定程度时，为快速生长阶段;到生长后期，生长已基本完成，生长速率降低，其高度最终处于在某一稳定数值上。植物的这种生长规律能够较好地模拟大坝的沉降特性。在具体应用时，根据大坝沉降观测数据，代入式(1)中，由数学算法将参数a、b、c拟合出来，当t→∞时的函数值即为大坝的最终沉降量，即参数a值。目前估算参数a、b、c的方法有多种，如三段法、Bryant法、二次对数法、拐点法、多项式拟合法、高斯最小二乘法、非线性回归最小二乘法等［5］。

1.2 沉降特性

为了把控坝体的质量和确保大坝的安全运行，对坝体及坝基进行沉降监测是最为常用的监测手段，目前坝体监测大多采用电磁式沉降仪和水管式沉降仪，坝体表面可以利用布设简易观测桩，利用水准仪或全站仪等进行监测。沉降监测一般沿坝体布设若干监测断面，在每个监测断面上布置监测点。如沿坝高布置在3个高程处，分别设在1/3、1/2、2/3坝高处。根据大坝的沉降观测数据分析其沉降特性是最为可靠的手段。

随着坝体的填筑，上覆重力越来越大，坝基逐渐产生沉降。从坝体填筑初期至填筑完成，坝基沉降大致经历3个阶段:①大坝填筑初期，填筑面积较大，受施工因素等影响，填筑高度和填筑速率较小，在坝基内引起的附加应力相对较小，沉降量相对较小，沉降缓慢;②大坝填筑中期，施工较为快速，填筑速率较高，填筑高度较大，大坝快速沉降，为大坝的主沉降阶段;③大坝填筑晚期，整个坝体基本完成，坝高增加缓慢，在坝基内引起的附加应力已基本不再增加，沉降趋缓，随着坝体填筑完毕后，沉降也基本完成，最终稳定在某一数值。大坝的这种沉降特性与Gompertz模型的3个阶段正好吻合，因此可以采用该模型来预测大坝的沉降量。

1.3 适用性验证

为了分析Gompertz模型在大坝沉降预测中的适用性，以及分析相对其他传统预测方法(双曲线模型、幂函数模型与对数函数模型)的优缺点，选取了某大坝的沉降观测数据(图1)，根据该数据对其沉降进行预测。由图1可知，Gompertz模型的预测曲线与沉降观测结果较好吻合，能够较好地适应大坝沉降3个阶段的特性，其预测精度要比其他传统模型好，由此可以判断Gompertz模型能够较好地预测大坝的沉降。

图1 Gompertz模型预测大坝沉降的适用性验证

2 实例应用

2.1 岭下溪水库大坝沉降预测

福建省岭下溪水库位于东溪支流庵下溪中游处，大坝在霞葛镇岭下溪村附近。汇雨面积为140 km2，水库正常蓄水位为183.4 m高程，库容为1 590 m3。该工程为混凝土浆砌石重力坝，副坝为均质土石坝。整个大坝包括引水隧洞、压力管道和水电站等建筑物。该重力坝平均高度为54.5 m，大坝长178 m，溢流段设置5个溢流孔，每孔净宽10 m，每个溢流孔均设有10 m×6.4 m弧形闸门扇，溢流堰堰顶高程为177.5 m。坝基为花岗岩风化残积粘性土，厚3.4～12.0 m，下部为强风化花岗岩和中风化花岗岩，深度未揭露。

为确保该坝体的施工质量和后期的安全运行，在整个大坝填筑过程中对其沉降量进行了观测，观测仪器采用电磁式沉降仪，填筑完毕后在坝顶布设沉降观测桩，利用水准仪对其进行观测。其中，坝中3个断面处坝基(桩号分别为K0+030、K0+102和K0+143)的沉降观测结果见图2。采用Gompertz模型对该监测结果进行预测，利用Matlab编写参数拟合程序，其中，K0+030处的3个参数拟合值分别为 a=－949.384 3、b=3.967 9、c=0.116 3;K0+102处的3个参数拟合值分别为a=－811.322 2、b=4.780 0、c=0.140 7;K0+143处的3个参数拟合值分别为a=－765.063 8、b=7.063 4、c=0.135 1。K0+030～K0+143监测断面处，坝基沉降越来越大，主要原因是后者的花岗岩风化残积土厚度要比前者大，即压缩土层的厚度大3.5 m;另外，后者的填筑高度比前者高2.7 m，因此在上部坝体荷载作用下，坝体沉降量要大121 mm。

该坝基沉降的实测数据与Gompertz模型的预测结果几乎完全重合，表明Gompertz模型具有较好的预测精度。当t→∞时，K0+030、K0+102、K0+143监测断面处的最终沉降量分别为949、811、765 mm。

图2 岭下溪水库大坝沉降预测结果

有时为了需要提前知道后期的沉降情况，工程可利用前期的沉降监测数据来预测后期的沉降结果。以最后一次观测数据为例，当利用不同时间的观测数据时，预测时间为53个月时的沉降值，结果汇总于表1。其中，误差=(预测值－实测值)/实测值×100%，取绝对值。可以看出，当利用较短时间的观测数据时，预测误差较大，随着观测时间越来越长，利用的观测数据越来越多，预测精度越来越高。当利用到35个月的观测数据时，3个监测断面处的预测误差均在5%以内。

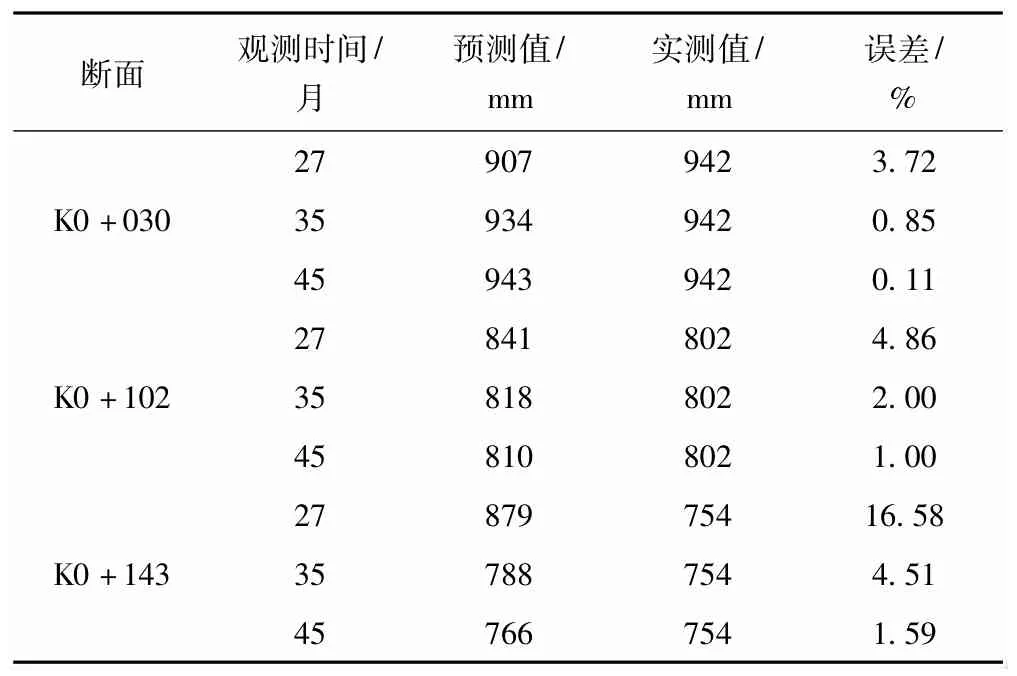
表1 利用不同观测时间时的预测结果

2.2 某混凝土面板坝沉降［2］

某混凝土面板坝最大坝高处，在坝顶下游侧设置了一条竖直测线，于40、70、100 m高程处分别安装了3层沉降仪观测点，其编号分别为 T01、T02、T03，并在坝顶处安装了表面沉降观测点T04。该坝于2002年8月1日开始填筑，在2003年3月底，坝体填筑到40 m高程后安装埋设沉降观测点T01，至2003年7月底，填筑到70 m高程时，安装T02观测点，5个月后，填筑到100 m高程时，安装T03观测点。以上述4处沉降观测点的实测数据为例，采用Gompertz模型预测不同时间的沉降量，预测结果汇总于表2。可以看出，各个监测点在不同时间时的预测精度均较高，最大误差为4.70%。

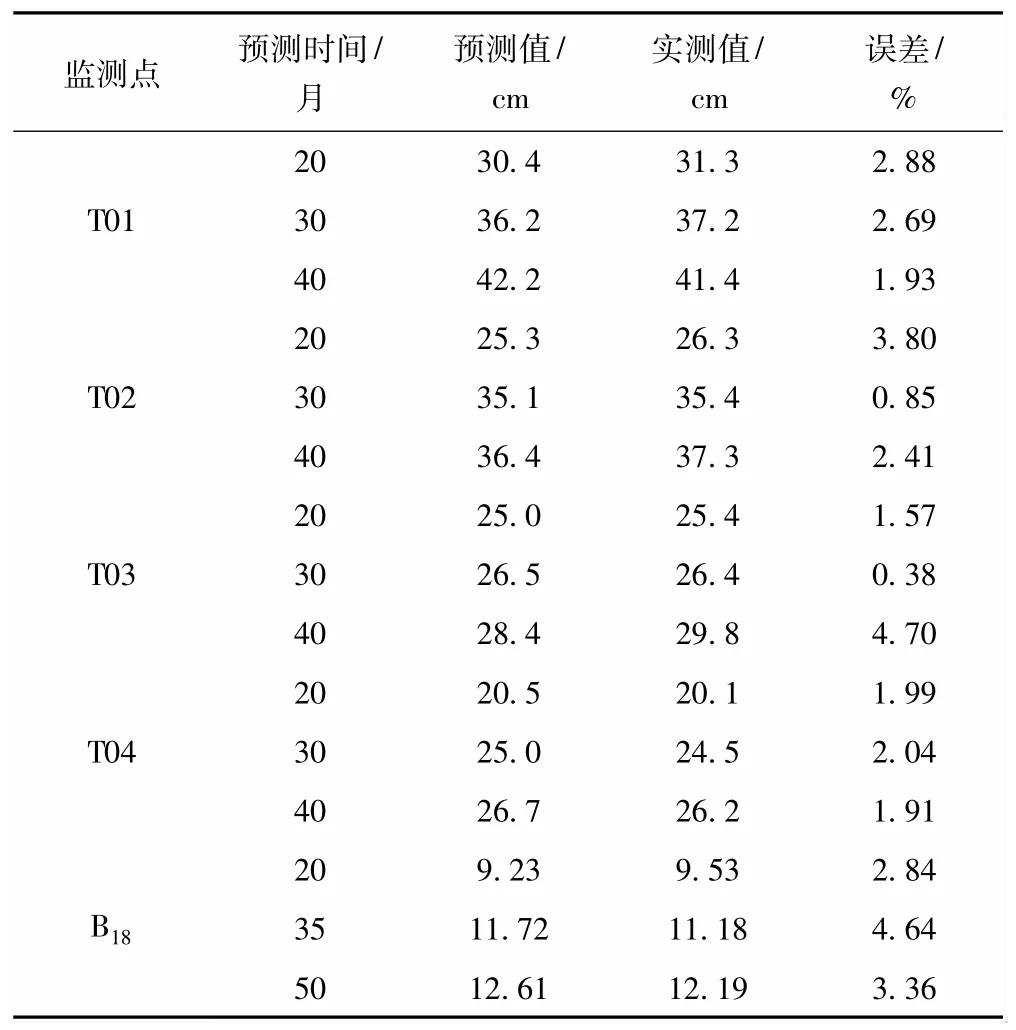
表2 两座大坝的沉降预测结果

2.3 某土石坝沉降［6］

文献［6］给出了某土石坝沉降观测点B18的沉降观测数据，结合其数据利用Gompertz模型预测观测时间在20、35、50个月时的沉降量，结果见表2，可知沉降观测点B18各个时间的预测结果与实测结果也非常接近，最大误差也控制在5%以内。

3 结论

针对大坝沉降的特点，提出采用Gompertz模型来预测其沉降量，通过验证发现Gompertz模型比传统的预测模型的预测精度要高。结合3个工程实例的观测数据，利用Gompertz模型对其沉降量进行了预测，结果发现预测值和实测值非常接近，最大误差均控制在5%以内。当利用前期观测数据预测后期沉降量时，随着观测时间越来越长，利用的观测数据越来越多，预测精度逐渐提高。

［1］金永强，顾冲时，于鹏．变权组合预测模型在大坝安全监测中的应用［J］．水电自动化与大坝监测，2006，30(5):60-62．

［2］王法西，张彬，赵峰．土石坝沉降及实测资料分析计算［J］．大坝与安全，2011(4):19-22．

［3］宋彦辉，聂德新．基础沉降预测的Verhulst模型［J］．岩土力学，2003，24(1):123-126．

［4］李玉花，黄林．BP神经网络在软土地基沉降预报中的应用［J］．岩土工程界，2007，10(5):30-32．

［5］杜勇立．单桩承载力预测的PSO-Gompertz模型研究［J］．公路工程，2012，37(5):87-91．

［6］朱忠荣，蔡启龙，寇国祥．组合预测模型在土石坝沉降分析中的应用［J］．水利与建筑工程学报，2005，3(1):53-55．