关于高中数学几何解题技巧之“数”“形”结合策略
陈樱芷
摘要:数学是一門研究数量关系和空间形式的学科,它在一定程度上深刻的反映了社会规律和自然规律。在高中数学学习的过程中都伴随有数学思想方法,它是整个高中数学学习不可或缺的内容。作为数学思想中最重要的方法之一,数形结合方法很好的使“数”和“形”联系到一起,将高中数学知识从不同的角度展现出来,而且还能够解决高中数学内容里的很多问题。
关键词:高中数学;几何;解题技巧;数形结合
高中阶段的学习过程是学生创新思维培养的重要时期,它有利于学生形成数学的创新思维。培养学生的数学创新思维,实际上是通过创新意识来感染和熏陶学生,帮助学生将所学习到的数学知识重新组合,最终形成新设想和新发现。解析几何在高考中占有非常大的比例,其难易程度低于函数部分,而且几何的解题一般具有技巧性。在解题的过程中合理正确的使用数形结合方法能够在很大程度上提高高中数学几何的成绩。
1高中数学中应用数形结合方法的原则
因为高中数学的题目变化万千,在解题的时候不能形成统一固定的方法和模式,在高中阶段解决几何问题过程中应用数形结合的方法,学生应该与自身的认知和学习的特点相符合,而且还必须要体现其学习价值,具体遵循的原则包括:首先,要遵循等价性的原则,即“数”与“形”在转换的时候必须使其对应的代数性质和几何性质保持一致,也就是说某道题的数量关系和图像表示必须具有一致性;其次,要遵循双向性原则,在解题的时候不仅要探索其代数的抽象,而且还要直观的分析其几何图形,代数关系的运算和表示避免了几何图形的局限性,而几何图形却更加直观;最后,还要遵循实践创新原则,高中数学思想方法非常的抽象,在解题的过程中是不可能复制和照搬的,所以学生在学习高中数学的过程中必须要对传统的学习方式和学习内容进行改革和创新,培养自己的数学思维能力。2数形结合的解题思想
数形结合思想实际上就是将题目中已知的“数”与对应的“形”结合起来,通过直观简单的图形将抽象复杂的数学语言转化成易于理解的数量关系,然后再结合抽象思维和形象思维,达到以数解形或以形助数的目的,化简单为复杂,变抽象为具体,最终实现解题方法的优化。
在解决解析几何相关的题目时,首先必须要明确问题与条件之间的位置关系和数量关系,并将其一一对应,从而快速准确的解决对应的几何题目。实际上,如果能够将数形结合方法熟练的掌握,并可以做到举一反三时,那么所有这类型的题目都能够轻易的找到解题思路了。要想将数形结合的解题方法熟练掌握,就必须将以下各种关系理顺:首先,三角函数和复数等与几何元素和几何条件为背景的概念;其次,题目已知的代数方程和等式中所要明显表达的含义;再次,图像与函数的对应关系、方程与曲线的对应关系;最后,数轴上点与实数的对应关系。3高中几何解题中数形结合方法的具体应用
3.1在三角函数中的应用
高中数学学习的重点内容是由数形结合、空间形式、数量关系等构成的,而三角函数是一种描述周期运动的模型,它是数形结合思想的产物。下面通过例题分析运用数形结合方法解决三角函数问题。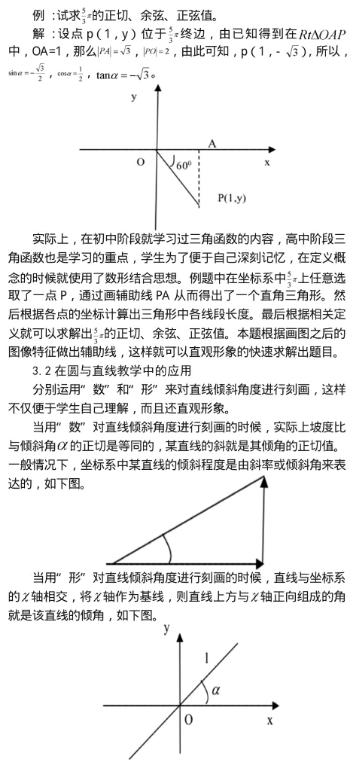
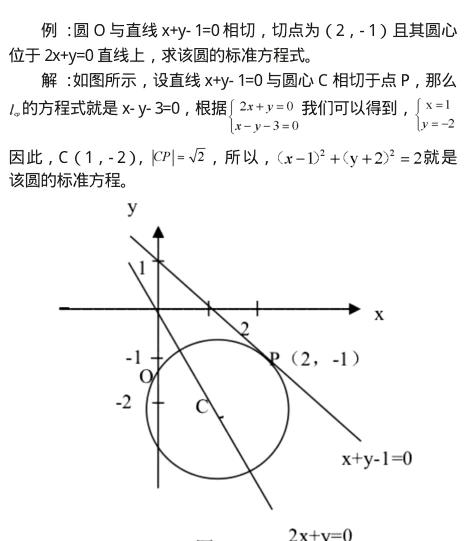
数形结合的思想在解决高中数学中圆类题目的时候具有非常大的作用,一般情况下,几何中的圆类问题基本上包括标准方程式、直线与圆位置关系以及圆与圆位置关系等内容。例如,在求解直线与圆的位置关系的过程中,可以首先建立直角坐标系,从而将圆与直线的位置直观的表现出来,然后再根据数形结合的思想求解出直线与圆心之间的距离,对比该距离与半径之间的大小判断出直线与圆的位置关系。
结语:学生在解决高中数学几何问题的过程中,应该加强对数形结合方法的应用,这样能够在一定程度上使自己的思维方式由静态变成动态,培养自身联系、变化、运动的观点来思考问题。学生在学习的过程中通过应用数形结合的方法能够培养自己分析和解决问题的能力,是其在解决问题时能够准确找到题目中数和形的连接点,然后再巧妙的将其结合起来。由此可知,数形结合方法在高中数学的几何解题中具有非常重要的作用,它是数学方法和数学思想的核心部分,每位高中学生都应该在学习过程中应用数形结合的方法。
参考文献
[1]姚爱梅.高中数学教学中数形结合方法的有效应用[J].学周刊,2011,12:50.
[2]李红梅.例谈数形结合在高中数学中的应用[J].新课程研究(基础教育),2010,05:177—178.
[3]陈益周.数形结合方法应用于高中数学教学的实践研究[J].兰州教育学院学报,2015,04:165—166.
[4]刘桂玲.数形结合思想方法在高中数学教学中的应用分析[J].中国校外教育,2015,13:106.

