基于复合模型动力蓄电池SOC估算

高顺荣， 谢慕君

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

蓄电池是电动汽车的心脏，需要对它管理和研究。在实际生活中用的很普遍的就是磷酸铁锂电池，因为它有很多其它电池不具备的优势。荷电状态(SOC)是蓄电池的一个重要指标，为了提升蓄电池的使用功效，有必要得到确切的SOC估测值。实际情况中对电池的使用有很多种要求，这就促使人们用许多不同的方式来获得确切的SOC，如安时计量法[1]、开路电压法[2]、卡尔曼滤波法[3]等；文中针对安时计量法不能估算电池初始状态及存在积累误差的问题，应用安时计量法、开路电压法及扩展卡尔曼滤波法相结合对电池SOC进行估计。通过安时计量法表达式离散化获得电池状态方程，引入电流系数及温度系数，获得电池的复合模型，再采用EKF估算磷酸铁锂电池的SOC。

1 基本原理

1.1 蓄电池SOC的概念

SOC定义为蓄电池目前剩余电量与在同样的放电前提下100%的电池能放出总容量的比值:

(1)

式中:Cd----剩余电量；

Ci----电池能放出的总容量；

CR----电池放出的电量。

1.2 安时计量法

安时计量法来计算SOC，不需要考虑磷酸铁锂电池里面的化学反应和结构变化，只需通过对电流的积分就能知道SOC。安时计量法表示如下：

(2)

式中:SOC(t)----电池在t时的SOC；

SOC(t0)----电池在t0时的SOC；

C0----电池的额定容量；

i----t时的电流；

η----i对应的充放电效率。

安时计量法在现实使用中存在一些问题：

1)SOC(t0)不容易获得，假如SOC(t0)计算不精确的话，最后计算出的值也会有些偏差；

2)由于电池的容量特征，电流i和温度T都会影响到电池的实际释放容量。

因此，为了获得确切的SOC，就要解决这两方面的问题。

1.3 开路电压法

电池停止工作以后，里面的电化学反应也会稳定下来，它的电压会逐渐达到一个恒定值，其中这个不变的电压就是电池的等效电动势(E)，再根据E-SOC关系就能知道SOC(t0)的值。

1.4 卡尔曼滤波法

KF能确切地估计SOC，在SOC的估算中，把电流和温度作为输入量，电池的端电压作为输出量，SOC作为状态变量[4]。磷酸铁锂电池是非线性系统，因此，采用EKF来估测SOC，EKF所使用的系统状态空间模型为[5]：

状态方程：

xj+1=h(xj,uj)+ωj

(3)

观测方程：

yj=g(xj,uj)+υj

(4)

式中：h(xj,uj)、g(xj,uj)----分别为状态转移函数和观测函数；

ωj----系统的状态噪声；

υj----系统的测量噪声。

2 复合模型的建立

在安时计量法中，为了考虑放电电流的大小和温度对电池实际释放容量的影响[6]，引入等效电流系数和温度系数，表达式如下：

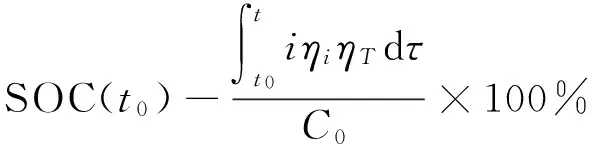
(5)

2.1 等效电流系数ηi

因为电池容量特征对SOC估测的干扰，把等效电流系数代入安时计量法中；1897年Peukert总结出一个公式，也称为Peukert方程，它主要是关于蓄电池恒流放电电流和持续时间的关系[7]。

int=Const

(6)

式中：i----放电电流；

t----充满的电池持续放电到截至电压的时间；

n----与电池类型有关的常数，取n=0.989 25[8]；

Const----和电池活性物质有关的固定值。

Ci=it表示电流为i时的可用容量，将它代入式(6)，得：

Ci=Const×i1-n

(7)

(8)

(9)

联合式(8)和式(9)可以解得：

(10)

再结合式(7)可求得等效电流系数ηi：

(11)

2.2 温度系数ηT

环境温度对电池容量也有干扰，一般来讲，随着周围温度的上升，电池释放的容量会有所增加，现在经常采用经验公式来描述温度与容量的关系[9]。

CT=C20[1+mT(T-20)]

(12)

式中:CT----T时的容量；

C20----20 ℃时刻的容量；

mT----常数，通常为0.006～0.008。

设

ηT=[1+mT(T-20)]-1

则有

若以20 ℃为标准，则C20就是额定容量C0。

2.3 模型建立

使用EKF估测电池SOC时，需要采用电池模型。把修正后的安时计量法式(5)用泰勒级数展开[10]，得：

(13)

其中，SOC是状态变量xj,得到了复合模型的状态方程：

(14)

复合模型的观测方程是由三种简单的电化学模型组合得到。

Shepherd模型:

(15)

Unnewehr universal模型:

yg=E0-Rig-Kixg

(16)

Nernst模型：

yg=E0-Rig+K2lnxg+K3ln(1-xg)

(17)

将Shepherd模型、Unnewehr universal模型和Nernst模型的模型函数多项式进行相加，统一模型参数，得复合模型的观测方程：

K3lnxj+K4ln(1-xj)

(18)

式中:ij----j时刻的电流；

yj----端电压；

R----固定阻值；

K0----磷酸铁锂的开路电压；

K1、K2、K3、K4----磷酸铁锂的模型参数，依据实验数据，再通过最小方差法计算获得涉及到的参数值。

3 估测电池SOC

根据上述过程创立模型，设计复合模型的卡尔曼滤波算法获得SOC[11]。

3.1 模型的选择

考虑环境温度T和电流i因素以后，得到修正后的电池复合模型的状态方程和观测方程如下：

xj+1=h(xj,uj)+ωj=

(19)

yj=g(xj,uj)+υj=

K3lnxj+K4ln(1-xj)+υj

(20)

3.2 系统动态特性匹配系数的确定

把电池模型的状态方程和观测方程用Taylor级数展开，并利用Jacobin矩阵求解得到模型匹配系数。状态方程里面的系数值为：

(21)

(22)

观测方程的动态匹配系数为：

(23)

(24)

另外，系统输入的求解表达式为：

uj=ij

(25)

通过上述推导可知状态方程：

xj+1=Ajxj+Bjuj+ωj

(26)

观测方程为：

yj=Cjxj+Djuj+υj

(27)

在具体过程中用Dω表示过程噪声误差，Dυ是观测噪声误差，EKF执行过程如图1所示。

图1 EKF的流程图

4 方法验证与分析

为了检验基于复合模型的EKF,可以很好地计算磷酸铁锂电池组的SOC,用实验室的磷酸铁锂电池组测量电池的SOC，历时600 s，采样间隔3 s，得到SOC的变化值。间隔30 s的部分实验数据见表1。

表1 部分实验数据

针对观测方程式(18)中的参数，令参数向量

ρ=[K0,R,K1,K2,K3,K4]T

矩阵

E=[e1,e2,…,eN]

矩阵E的列向量

定义向量

Y=[y1,y2,…,yN]

模型观测方程可等效为

Y=Eρ

因此，利用已知的Y和E就可以求出参数向量ρ，即

ρ=(ETE)-1ETY

其中，磷酸铁锂电池组的模型参数计算值[12]见表2。

表2 模型参数

在SOC理论算法推导的基础上，采用Matlab进行仿真实验，检验基于复合模型的EKF能很好地计算磷酸铁锂电池组的SOC。从仿真实验看出，采用EKF估算出复合模型的SOC值，根据时间的变化可以很快地逼近测量值，如图2所示。

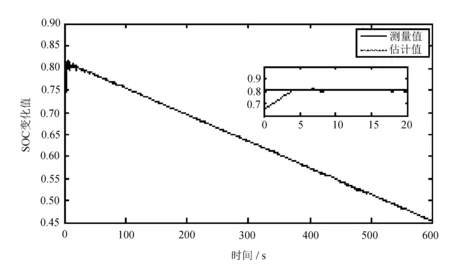
图2 SOC计算值与实验值的对比

将复合模型计算的SOC仿真结果与实验室的测量值进行对比，误差刚开始还有点明显，但减小的非常迅速，这在一定程度上也表明,基于复合模型的卡尔曼滤波算法具有很好的初值收敛性，误差曲线如图3所示。

图3 SOC误差曲线

5 结 语

通过安时计量法表达式离散化获得了磷酸铁锂电池组的状态方程，引入等效电流系数和温度系数实现电池容量的修正，建立了电池组的非线性复合模型，应用扩展卡尔曼滤波法估计电池SOC，解决了安时计量法不能估算电池初始状态和存在累积误差的问题。仿真实验表明,该方法能很好地逼近实验室电池组SOC测量值，且可行有效。

[1] 詹世安.磷酸铁锂电池荷电状态估算方法研究[J].电源技术,2015(8):1620-1622.

[2] X Zhang, X Wang, W Zhang, et al. A simplified li-ion battery SOC estimating method[J]. Transaction on Electrical & Electric Materials,2016,17(1):13-17.

[3] 李慧,肖伟,骆万博.电池剩余电量SOC估计[J].长春工业大学学报,2017,38(1):73-78.

[4] L Gregory. Plett. Extended Kalman filering for battery management systems of LiPB-based HEV battery packs[J]. Journal of Power Sources,2004,134:252-292.

[5] A Jossen, V Spath, H Doring, et al. Reliable battery operation-a challenge for the battery management systems[J]. Journal of Power Sources,1999,84:283-286.

[6] 张金龙.动力电池组SOC估算及均衡控制方法研究[D].天津:天津大学,2011.

[7] 崔立丰,高飞,王永武,等.磷酸铁锂动力电池Peukert方程修正模型的研究[C]//第六届中国智能交通年会暨第七届国际节能与新能源汽车创新发展论坛.2011.

[8] 仝猛,卢兰光,欧阳明高,等.Peuker方程的适用性分析及基于二阶段放电法的Peukert模型修正[J].机械工程学报,2010,46(10):121-125.

[9] 齐国光,李建民,郏航,等.电动汽车电量计量技术的研究[J].清华大学学报:自然科学版,1997,37(3):46-49.

[10] 朱敏.基于电动车电池组SOC估计方法的研究[D].郑州:河南师范大学,2014.

[11] 何灵娜.基于卡尔曼滤波的动力电池SOC估计算法设计[D].杭州:浙江工业大学,2014.

[12] 徐杰.基于卡尔曼滤波的动力电池组SOC精确估计[D].杭州:杭州电子科技大学,2009.