一种电能计量设备运维作业动态优化模型及算法

唐若笠++方彦军

摘 要：针对电网企业传统模式下运维作业所存在的任务分配不科学、路径规划不合理和无法实时响应动态需求等问题，提出了一种新的动态优化模型及求解算法.该模型能够对运维作业的任务点数量、实时路况、运维人员属性与数量、决策者偏好等外部条件予以实时动态响应，满足电网企业日常管理工作需求.此外，针对模型特点提出一种基于解空间分割的粒子群算法（PSO-SSD）进行运维作业路径优化.仿真实验表明，本文所提出的动态优化模型及PSO-SSD算法能够在不同问题规模下保持优良性能，实现电能计量设备运维作业的实时动态优化，有效提升电网企业管理工作效率.

关键词：电能计量设备；运维作业；动态优化；粒子群算法

中图分类号：TP18 文献标志码：A

Research on Dynamic Optimization Model and Algorithm

of Electric Meters Operation and Maintenance Task

TANG Ruoli1， FANG Yanjun2

（1. School of Energy and Power Engineering， Wuhan University of Technology， Wuhan 430063，China；

2. Department of Automation，Wuhan University，Wuhan 430072， China）

Abstract：As influenced by the improved requirement of electric meters operation and maintenance task （EM-OMT）， the traditional mode is not applicable to the new management needs any more. In terms of the existing problems in the traditional operation mode， for instance， the unscientific allocation of tasks， the unreasonable planning of path and no response to the dynamic requirements in time， a novel dynamic optimization model and algorithm was proposed. The quantity of tasks， real time traffic condition， attribute and quantity of workers， and preference of the decision maker as well as some other outside conditions can be responded dynamically by the proposed model， which satisfies the daily requirement of power grid enterprise effectively. Furthermore， considering the characteristics of the model， a novel PSO with Solution Space Decomposition（PSO-SSD） algorithm was also proposed and applied to the path optimization. Simulation result shows that the proposed dynamic optimization model and PSO-SSD algorithm can obtain a good performance on different scale of problems， and provide the dynamic optimization of electric meters operation and maintenance task， which significantly improves the management efficiency of power grid enterprise.

Key words：electric meters； operation and maintenance task； dynamic optimization； particle swarm optimization

隨着网络化、信息化技术在电力行业的深入推广，传统的电能计量设备运维作业模式早已无法满足新的需求，其存在的任务分配不科学，路径规划不合理，作业过程耗时长、能耗高，以及无法实时动态响应决策变化等问题，严重影响电网企业的日常管理工作效率.

目前国内外关于电能计量设备运维作业优化的相关研究主要是通过信息化、网络化技术的应用，替代传统手工与经验作业模式，并未涉及统筹时间、路程、能耗、效率等要素的优化及动态调整问题.如南方电网公司进行了电能计量运维现场作业信息系统的研制，并在佛山供电局计量中心进行试点应用[1].广东电网公司东莞供电局也开展了基于移动作业终端的电力计量设备运维管理系统研制工作[2]，在移动终端上实现了计量装置的定位导航、设备信息展示以及现场辅助交互等功能.然而，目前关于电能计量设备运维作业优化的研究尚无法切实满足电网企业的管理需求，有必要进一步研究合理、高效的运维作业优化方案，在充分考虑时间、路程、能耗、效率等要素的前提下，科学分配运维任务，合理规划作业路径，进而降低运维作业成本，对于提升电网企业运维工作效率具有重要意义.

本文围绕电能计量设备运维作业动态优化模型及算法展开研究，重点关注电网企业实际管理需求，建立能够对任务点数量、实时路况、运维人员属性与数量、决策者偏好等外部条件予以实时动态响应的优化模型，并针对模型特点提出高效的求解算法，以实现电能计量设备运维作业的实时、动态优化.

1 电能计量设备运维作业管理需求分析

电网企业每日需对一定数量且分布于不同位置的计量设备进行运维作业.为提高管理效率，降低工作成本，电网企业进行电能计量设备运维作业优化管理的具体需求包括以下几方面：

1）根据每日出勤作业人员人数以及业务能力的不同，科学地进行任务量分配；

2）将规划路径的路程长度、交通状况等要素纳入评价标准，综合考虑时间、路程、能耗最优，实现对运维作业路径的实时优化；

3）当个别作业人员出现特殊情况无法继续完成运维任务，或有新的作业人员加入运维工作时，要求优化模型能够实时地实现作业人员的调入和调出，并同时保证任务分配与路径规划的最优；

4）在运维工作进行过程中，当出现新的任务点需要被处理时，要求能够将其实时加入当日运维任务，并安排合适的人员对其进行操作；

5）要求优化模型能够实时输出并更新各运维人员的有序任务列表和行进路线，并以一定方式发送至对应作业人员的手机APP终端，以指导其作业过程.

2 电能计量设备运维作业动态优化模型

为进行电能计量设备运维作业动态优化管理，首先应建立相应的优化模型，以实现对电网企业上述管理需求的实时响应.本文提出的优化模型包括任务编解码以及在其基础上建立的动态优化目标函数与算法编解码，三者共同构成了电能计量设备运维作业动态优化的完整数学模型.

2.1 动态优化模型的任务编解码

所谓任务编解码，是指实现实际问题（即各运维人员有序任务列表）与数学模型之间的转化，且要求能够对实际需求予以响应.本文采用将各运维人员有序任务列表首尾相接并在连接处添加分隔符的方式进行任务编解码.具体地讲，以N个运维任务点，P个出勤作业人员为例，则优化向量为：

x=（x1，x2，x3，…，xN），xi∈{1，2，3，…，N} （1）

式中：xi为对应任务点序号.所有xi的取值不重复，即优化向量x总是1， 2， …， N的一个排列.

每日可根据运维任务量及实际出勤人员人数、业务能力的不同，按照一定原则科学指定各作业人员的任务数量.假设根据任务量、出勤人数以及业务水平等要素指定的任务量分配情况为：运维人员编号1-P对应的任务量依次为n1，n2，…，nP，则优化向量x的前n1维表示1号作业人员的有序任务列表，之后的n2维表示2号作业人员的有序任务列表，且第n1维与第n1+1维之间添加分隔符，以此类推.每一作业人员都分别依次执行其有序任务列表中的任务序号，则每一组优化向量x都能够解码为P个有序的任务路径，即一套完整的作业任务分配和路径规划方案，如图1所示.可见，该方式能够通过调整参数N，P以及分割符位置，实现对任务点数量、运维人员属性与数量的动态响应.

2.2 动态优化模型的目标函数

2.2.1 路况系数

定义路况系数（c）以反映不同的交通状况对运维路径规划产生的影响.具体地讲，首先将实时路况分为通畅、缓行、拥堵和严重拥堵4个等级，分别与平均车速60，30，10以及3 km/h相对应.在只考虑时间而不考虑能耗的情况下，各路况所对应的路况系数应为平均车速的倒数比，即

ct1：ct2：ct3：ct4=160：130：110：13=1∶2∶6∶20（2）

式中：ct1，ct2，ct3，ct4分别表示通畅、缓行、拥堵、严重拥堵4种路况在仅考虑时间要素下的路况系数.可见，当缓行、拥堵、严重拥堵的路程分别低于通畅路程的2倍、6倍与20倍时选择绕行，以保证时间最短.然而，在综合考虑能耗的情况下，这显然不是一种合理的方案.

按照车辆平均油耗与时速的对应关系，在只考虑能耗的情况下，各路况所对应的路况系数应为不同车速下的平均油耗比.本文按式（3）进行取值：

ce1：ce2：ce3：ce4=1∶1.5∶2.5∶4（3）

式中：ce1，ce2，ce3，ce4分别表示通畅、缓行、拥堵、严重拥堵4种路况在仅考虑能耗时的路况系数.

进一步地，定义时间权重pt与能耗权重pe对这两个要素进行加权求和，电网企业可根据实际情况对权重值进行动态调整，以响应决策者偏好，这也进一步体现出“动态优化”的概念.综上所述，路况系数的定义如式（4）所示：

ci=ptcti+pecei，i=1，2，3，4；s.t.pt+pe=1 （4）

2.2.2 代价矩阵

在每一次运维路径规划之前，首先按照式（5）与式（6）所示生成代价矩阵：

C=r11·c11r12·c12…r1N·c1Nr21·c21r22·c22…r2N·c2NrN1·cN1rN2·cN2...rNN·cNN （5）

C0=r01·c01r02·c02…r0N·c0Nr10·c10r20·c20…rN0·cN0（6）

式中：rij （i， j=1，2，…，N）为第i个任务点至第j个任务点的路径长度（0表示运维中心）；cij为对应路径的路况系数；N为当日需要运维的任务点数量.

注意到，由于路况系数的非对称性，任意两点之间往返的路径代价并不一定相同，即代价矩阵C为非对称矩阵，这使得2-opt等常规启发式算法不再适用，也在一定程度上增加了采用智能算法求解该问题的难度.

2.2.3 目标函数

最后，根据图1所示编解码方式中分隔符的位置，解碼出各作业人员的行进回路，并依次加总所有闭合回路的综合代价系数，作为整个作业方案对应的目标函数值，如式（7）所示：

f（x）=∑Pi=1[ρ0xi1+∑ni-1s=1（ρxisxi（s+1））+ρ0xini]（7）

式中：P为当日出勤的作业人员数量；ni表示第i号作业人员的运维任务量；ρxisxi（s+1）为代价矩阵C的对应元素，xis与xi（s+1）分别为第i号作业人员任务列表中第s及第s+1个任务点；ρ0xi1与ρ0xini为代价矩阵C0的对应元素，xi1与xini分别为第i号作业人员任务列表中第1个及第ni个任务点.

2.3 动态优化模型的算法编解码

由上述任务编解码方式及目标函数可以看出，该模型目标函数值的计算采用离散方式进行.考虑到大多数智能算法均基于连续数值运算，本文拟建立一种变量维度间相对大小排序的算法编解码方式，以实现算法与模型的对接.具体地讲，对于算法中某一连续编码的个体x，在计算其目标函数值前首先对其各维度的变量数值按照相对大小进行排序，并同时标注序号，然后将每一维度的数值转换为相应的序号，进而个体x能够被转换为式（1）所示的1至N的排列形式.此外，可通过设置较高的连续编码个体x 的運算精确度（如10-5），使排序过程中个体x出现相等维度变量值的概率几乎为零，进而保证排序操作的顺利进行.

以目标任务点数量N=10，出勤作业人员数量P=2为例，每一维度变量取值范围设置为[-1， 1]，计算个体x的目标函数值时的算法编解码过程如图2所示，其中0表示运维中心.

x=（-0.924 15，-0.401 4，0.516 25，0.141 87，0.229 57，

0.984 75，0.844 55，0.591 97，0.015 97，-0.804 58）

3 电能计量设备运维作业动态优化算法

随着智能算法的提出与不断发展，其已形成诸多不同的算法分支[3-5].其中，粒子群算法（Particle Swarm Optimization， PSO）由于规则简单且性能良好，被国内外学者进行不同程度改进并成功应用于解决各类优化相关的技术问题[6-8].

本文针对上述模型特点，提出一种基于解空间分割的粒子群算法（PSO with Solution Space Decomposition， PSO-SSD），以解决电能计量设备运维作业的动态优化问题.由于2.3节所提出的算法编解码采用相对大小排序的方式进行，这在一定程度上放大了解空间，进而增加了算法的求解难度.PSO-SSD采用解空间分割的方式对不同维度变量分别求解，并定义参考向量（Context Vector， CV）进行子空间相互之间的信息传递与解空间重构.具体地讲，以D维问题为例，初始化规模为NP的种群P，则P为NP×D的矩阵.将矩阵P按列随机分为K组，即P = [PS1， PS2， … ， PSK]，且K=D/s，s为每一组包含的变量数目，即每一子问题的规模.PSO-SSD采用动态组规模机制，即s从预先设定好的组规模序列S中随机初始化，如S={1， 2， 5， 10， 20， 50}，且算法每一代判定当前最优解是否有进化，若有则保持s不变，若无则s从序列S中重新选取.

按上述方式进行分割后，D维解空间被拆分为K个s维子空间，进而D维种群P的进化被转化为K个s维子种群PSi （i = 1， 2， …， K）的协同进化.算法每一代依次遍历各子种群，且子种群内部按具体算法规则进化每一粒子个体.由于各子问题仅对应原始D维问题的部分变量，无法直接计算子种群个体的目标函数值.PSO-SSD定义参考向量解决这一问题：D维参考向量由其各维度对应的子种群最优个体构成，每一子种群在计算其个体的目标函数值时，所缺维度全部由CV对应维度变量值进行填补.

此外，PSO-SSD采用高斯分布生成每一粒子个体的新位置，如式（8）所示.其中，X（i/j）t+1表示第j个子种群中第i个粒子在第t代时生成的t+1代新位置；Pl（i/j）t与Pg（i/j）t分别表示该粒子对应的个体最优与全局最优（与子种群j的变量相对应）；N（0， 1）为标准正态分布（高斯分布）.综上所述，PSO-SSD算法流程如表1所示.

X（i/j）t+1=12（Pl（i/j）t+Pg（i/j）t）+

N（0，1）Pl（i/j）t-Pg（i/j）t（8）

4 电能计量设备运维作业动态优化仿真

分析

为验证本文所建立模型及优化算法的有效性，采用不同规模的运维优化问题进行数值实验，并与若干性能优良的智能算法进行对比分析.

4.1 实验参数设置

分别以15个任务点3人出勤、50个任务点5人出勤以及100个任务点10人出勤为例进行实验，并依次记为：Problem15，Problem50，Problem100.任务点及运维中心的位置坐标在0～50 km内随机初始化，时间权重pt取0.3，能耗权重pe取0.7，则路况系数取值及其随机初始化概率如表2所示.

选取基本PSO[9]以及CCPSO2[10]，SaDE[11]等算法进行对比实验.对于Problem15，所有算法种群规模设为50，算法终止条件设为目标函数达到最大调用次数max_FES=2×106；对于Problem50与Problem100，种群规模设为200，终止条件为max_FES=5×107.各算法对于不同问题均独立重复运行25次.参数设置如表3所示.其中，S为PSO-SSD及CCPSO2的组规模序列，p为CCPSO2的速度选择概率[10]；c1， c2为PSO加速度因子，ω为其惯性权重[9]；CRm， Fm为SaDE算法中选择因子CR与变异因子F的高斯分布均值，σCR，σF分别为对应高斯分布的标准差[11].

4.2 Problem15仿真分析

对于15个任务点3人出勤的问题，设各作业人员任务量按照n1=n2=n3=5进行分配.首先基于枚举法（A1515=15！≈1.31×1012次目标函数调用）计算得到Problem15的理论最优解为（7， 9， 14， 13， 1， 6， 2， 4， 3， 11， 15， 10， 5， 8， 12），其与各算法优化结果的对比情况如表4所示.可见，对于较小规模的Problem15求解，PSO与CCPSO2误差较大，SaDE误差相对较小，而PSO-SSD能够准确给出等同于枚举法的理论最优解，但其所消耗的计算资源仅为2×106，远低于枚举法的1.31×1012.

4.3 Problem50仿真分析

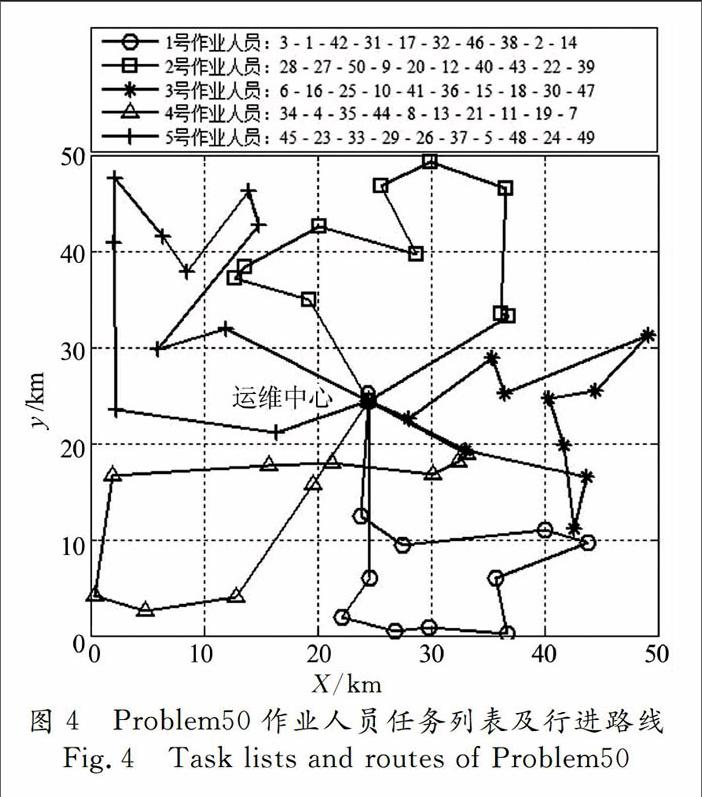
对于50个任务点5人出勤的问题，设各作业人员任务量按照n1=n2=n3=n4=n5=10进行分配.枚举法需A5050=50！≈3.04×1064次目标函数调用才能给出理论最优解，在可接受的时间范围内已无法完成.将Problem50作为理论最优解未知问题进行优化，各算法计算结果如表5所示，对应的进化曲线如图3所示，其中纵坐标f表示目标函数值，横坐标FES-pop表示目标函数调用次数与种群规模的比值.此外，各算法与PSO-SSD在5%显著性水平下的Wilcoxon秩和检验结果的p值与h值同样列于表中.可见，当问题规模增至50维时，包括SaDE在内的算法性能退化较快，而PSO-SSD依然能够保持较好的优化性能.基于PSO-SSD一次运算给出的最优解，Problem50各运维作业人员的任务列表及行进路线如图4所示.

4.4 Problem100仿真分析

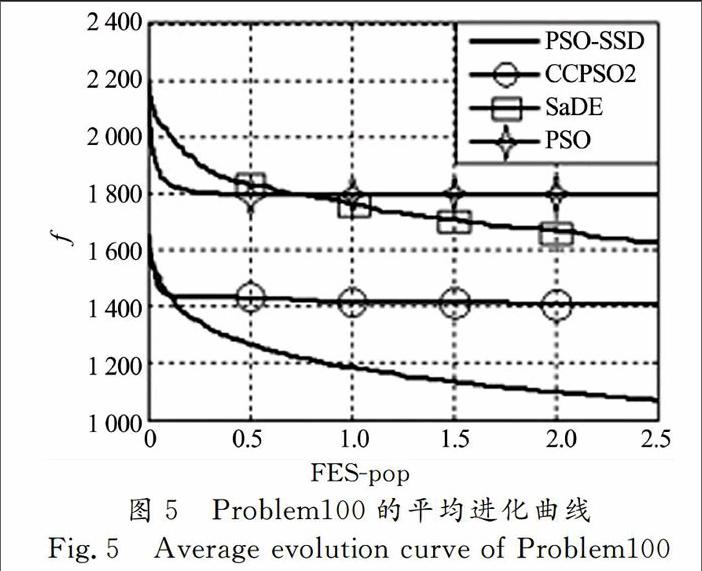
对于更大规模的Problem100，即包含100個任务点并有10人出勤，设考虑到不同人员的业务能力，任务量按10，10，10，10，10，18，15，6，6，5进行不均匀分配.各算法优化结果及进化曲线分别如表6及图5所示.可见，对于维数较高的Problem100，PSO及SaDE算法退化严重，而针对大规模问题设计的CCPSO2算法优化性能反超SaDE.PSO-SSD算法依然能够保证优良性能，完成100维的电能计量设备运维作业实时优化.

4.5 电能计量设备运维作业的动态优化

为验证本文所提模型与算法对电网企业动态要求的响应情况，以12个任务点4个作业人员为例进行动态优化仿真实验.具体动态任务过程设置如下：

1） 作业人员前往各自首个任务点开始作业时，4号人员完成其首个任务后需临时撤离；

2） 4号人员撤离后，触发更新操作，未完成任务依据业务能力按照n1=n2=3，n3=2进行分配；

3） 2号作业人员完成其首个运维任务并触发更新操作，此时选中路径的路况并未出现显著变化；

4） 1号作业人员完成其首个运维任务并触发更新操作，此时某一选中路径的路况出现严重拥堵.

采用PSO-SSD对上述问题进行求解，算法参数设置同Problem15，动态优化结果如图6所示.其中：（1），（2），（3），（4）分别表示各作业人员，1至12表示各任务点，0表示运维中心，“*”表示对应作业人员当前所处的任务点.由图6可以看出模型与算法对上述动态过程的响应如下：

1） 首先根据任务量、人员数量、路程以及实时路况等要素给出最优路径方案：1号人员0-11-8-4-0；2号人员0-6-7-1-0；3号人员0-3-5-12-0；4号人员0-9-10-2-0（如图6（a）所示）.

2） 当各作业人员分别前往各自首个任务点后，4号作业人员完成其首个任务即9号点后撤离，算法重新给出最优路径方案：1号人员11-8-4-12-0；2号人员6-7-1-5-0；3号人员3-10-2-0（如图6（b）所示）.可见，4号人员未完成的10号与2号任务点被3号人员接替，而原本3号人员未完成的5号与12号任务点分别被1号与2号人员接替.

3） 当2号人员完成其首个任务即6号点并触发更新操作后，由于被选中路径的路况并未发生显著变化，算法重新给出的最优路径方案不变，2号人员继续前往其下一个任务即7号点（如图6（c）所示）.

4） 当1号人员完成其首个任务即11号点并触发更新操作后，由于被选中路径中11号任务点至8号任务点路径出现严重拥堵，算法重新给出的最优路径方案为：1号人员11-4-8-12-0；2号人员7-1-5-0；3号人员3-10-2-0（如图6（d）所示）.可见，1号人员对其运维路径11-8-4进行了调整，变为11-4-8，从而规避了11-8的拥堵路段.

5） 各作业人员按上述方式重复运行算法，更新作业路径并依次完成剩余任务，最终全员返回运维中心，当日运维作业结束.

综上所述，本文所提出的模型与算法能够实时响应任务点数量、实时路况、运维人员属性与数量、决策者偏好等外部条件的变化，给出当前条件下符合要求的全局最优路径，满足电网企业对于电能计量设备运维作业日常管理工作的各项要求，进而实现运维作业的实时动态优化.

5 结 论

本文基于对电网企业电能计量设备运维作业动态优化管理的需求分析，建立了运维作业动态优化模型并提出基于解空间分割的PSO-SSD优化算法.仿真结果表明，所建立的模型能够对任务点数量、实时路况、运维人员属性与数量、决策者偏好等外部条件予以实时响应，且PSO-SSD算法针对不同规模的运维作业动态优化问题求解性能良好，二者共同实现电能计量设备运维作业的实时动态优化，对于提升电网企业日常管理工作效率具有重要意义.

参考文献

[1] 刘欣欣， 梁旭常， 刘攸坚， 等. 电能计量设备运维现场作业信息系统的研制[J]. 电测与仪表， 2014， 51（22）： 12-16.

LIU Xinxin， LIANG Xuchang， LIU Youjian，et al. Development of the on-site information system for the electric energy metering operations[J]. Electrical Measurement & Instrumentation， 2014， 51（22）： 12-16. （In Chinese）

[2] 李朔宇， 田纯青， 梁超慧. 基于移动作业终端的电力计量装置运维管理系统[J]. 现代计算机， 2014， 29： 69-72.

LI Shuoyu， TIAN Chunqing， LIANG Chaohui. Power metering device operation and maintenance management system based on mobile operations terminal[J]. Modern Computer， 2014， 29： 69-72. （In Chinese）

[3] TANG Ruoli， FANG Yanjun. Modification of particle swarm optimization with human simulated property[J]. Neurocomputing， 2014， 153： 319-331.

[4] 吳亮红， 王耀南， 袁小芳， 等. 多目标优化问题的差分进化算法研究[J]. 湖南大学学报：自然科学版， 2009， 36（2）： 53-57.

WU Lianghong， WANG Yaonan， YUAN Xiaofang， et al. Research on differential evolution algorithm for MOPs[J]. Journal of Hunan University：Natural Sciences， 2009， 36（2）： 53-57. （In Chinese）

[5] 巩敦卫， 陈健， 孙晓燕. 新的基于相似度估计个体适应值的交互式遗传算法[J]. 控制理论与应用， 2013， 30（5）： 558-566.

GONG Dunwei， CHEN Jian， SUN Xiaoyan. Novel interactive genetic algorithm for estimating individual fitness based on similarity[J]. Control Theory & Applications， 2013， 30（5）： 558-566. （In Chinese）

[6] KUMAR N，VIDYARTHI D P.A model for resource- constrained project scheduling using adaptive PSO[J]. Soft Computing， 2016， 20（4）： 1565-1580.

[7] GUEDRIA N N.Improved accelerated PSO algorithm for mechanical engineering optimization problems[J]. Applied Soft Computing， 2016， 40： 455-467.

[8] 任毅如， 张田田， 曾令斌. 基于遗传算法的潮流能水轮机翼型优化设计[J]. 湖南大学学报：自然科学版， 2015， 42（10）： 59-64.

REN Yiru， ZHANG Tiantian， ZENG Lingbin.Tidal turbine hydrofoil design method based on genetic algorithm[J]. Journal of Hunan University ：Natural Sciences， 2015， 42 （10）： 59-64.（In Chinese）

[9] EBERHART R C，KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro-Machine and Human Science. Nagoya，1995： 39-43.

[10]LI X D，YAO X. Cooperatively coevolving particle swarms for large-scale optimization[J].IEEE Transactions on Evolutionary Computation， 2012， 16（2）： 210-224.

[11]QIN A K，SUGANTHAN P N. Self-adaptive differential evolution algorithm for numerical optimization[C]//2005 IEEE Congress on Evolutionary Computation. Edinburgh：IEEE， 2005（1/3）： 1785- 1791.