模块化多电平变流器输出电流谐波抑制策略

荣飞+田新华+黄守道+王辉

摘 要：最近电平逼近是模块化多电平逆变器（MMC）常用的调制方法之一，当模块数偏少，或者调制电压过低时，输出电流会产生畸变.从原理上分析了MMC输出电流谐波畸变产生的原因，然后提出了一种抑制MMC输出电流谐波的控制方法.该方法对输出电流进行分频提取后通过PI调节器得到反相谐波电压，最后将反相谐波电压叠加到调制电压上获得总的参考电压.所提出的方法简单可行，易于实现.仿真分析和实验结果表明，采用本文所提出的方法，模块化多电平变流器输出电流的畸变得到较好的抑制.

关键词：谐波抑制；稳压控制；最近电平逼近；模块化多电平变流器；广义积分器

中图分类号：TM46 文獻标志码：A

Harmonic Suppression Strategy of Output

Current for Modular Multilevel Converter

RONG Fei，TIAN Xinhua，HUANG Shoudao，WANG Hui

（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Abstract：Nearest level modulation is a common modulation method for Modular Multilevel Converters （MMC）. As the number of modules is few or the modulation voltage is low， the output current is distorted. Firstly， this paper theoretically analyzes the reason why the harmonic of output current is distorted in MMC， and then proposes a control method to suppress the harmonics. The method extracts the harmonics of output current， and through a proportional integral regulator， the negative harmonic voltages is obtained. Lastly， the harmonic voltages are added to the modulation reference voltage. The purpose of this method is to obtain the total reference voltage. The proposed method is simple， feasible， and easy to implement. The simulation and experimental results show that the distortion of the output current of MMC is suppressed by the proposed method.

Key words：harmonics suppression； voltage control； nearest level modulation； modular multilevel converter； generalized intergrator

模块化多电平变流器采用子模块级联形式，每个子模块由单独的电容和开关器件构成，避免了大量开关器件的直接串联，具有良好的输出特性，且不存在动态均压的问题，非常适合高压直流输电领域[1-4].

传统的MMC控制方法主要集中在调制策略和控制策略的改进上.最常用的调制方法有最近电平逼近调制和载波移相调制.载波移相调制策略受到载波频率的限制，要求各子模块都采用频率相同、相位不同的载波，即每个子模块的载波不同，这对于电平数较多的系统而言过于复杂，并且要求每个子模块开关频率相同[5-7].最近电平逼近不需要载波信号，非常适合MMC结构.当输出的电平数比较多时，可获得比较好的调制波形.但是，由于最近电平逼近是用阶梯波对调制波进行逼近，在一个周期内采用的阶梯波个数有限，使得MMC的输出电流存在很大的谐波[8-10].因此，研究消除由最近电平逼近调制所带来的谐波具有重要的实际意义.

基于上述问题，本文提出了一种抑制模块化多电平变流器输出电流谐波的方法，对输出电流进行分频提取后通过PI调节器得到反相谐波电压，最后将反相谐波电压叠加到调制电压上获得总的参考电压.该方法操作简单，易于实现.

1 模块化多电平变流器的谐波分析

1.1 模块化多电平变流器的拓扑结构

MMC的结构如图1所示.系统采用三相六桥臂拓扑结构，每相包括上、下两个桥臂，每个桥臂由N个SM子模块和1个电感L串联而成，通过增加子模块单元的数量即可以实现对主电路的扩容.每相上桥臂的N个SM子模块和1个电感L依次串联，每相下桥臂的电感L和N个SM子模块依次串联，上桥臂和下桥臂连接点引出相线；3条相线接入公共电网.

MMC子模块单元通常采用单相半桥结构，每个子模块单元相当于一个可控的电压源，由2个IGBT管T1和T2，2个二极管D1和D2和一个电容C构成.子模块共有 3种运行状态：

1）当T1导通，T2关断时，处于投入状态，子模块输出电压为储能电容电压Uci，当Ism>0时，子模块电容处于充电状态，当Ism<0时，子模块电容处于放电状态.

2）当T1关断，T2导通时，处于切除状态，子模块输出电压为0，不管Ism是大于零还是小于零，子模块电容处于保持状态.

3）当VT1与VT2均关断，用于换流器子模块充电或故障时开关器件闭锁，处于闭锁状态，正常情况下不会出现此状态.

通过给IGBT适当的触发脉冲，控制子模块的工作模式，使得子模块单元输出的电压值不同，从而实现上下桥臂电压的叠加.通过对模块化多电平变流器（MMC）单相的分析，每相输出电压表达式为：

Uq=-Uqp-LdIqpdt+12UdcUq=Uqn+LdIqndt-12Udc （1）

式中：q=a，b，c，表示a，b，c三相；Uq为相电压；Uqp为该相上桥臂子模块电压之和；Uqn为该相下桥臂子模块电压之和；Iqp为该相上桥臂电流；Iqn為该相下桥臂电流.

由MMC相关知识可得：

Uqp=12Udc-Uq-12LdIqdt-UcircqUqn=12Udc+Uq+12LdIqdt-Ucircq （2）

1.2 谐波分析

最近电平逼近（Nearest Level Modulation，NLM）调制是模块化多电平常用的调制方法之一，在任意时刻，通过设置MMC的下桥臂和上桥臂需要投入的子模块数来形成阶梯波，就可以逼近调制波，如图2所示.

由于是采用NLM方法来逼近调制波，即用阶梯波来逼近调制波，因此也不可避免地带来了不小的谐波.下面通过傅里叶分解阶梯波来对这种情况下的谐波进行分析.

根据数学知识可知，如果给定的周期函数f（t）满足狄里赫条件，即：①周期函数极值点的数目为有限个；②间断点的数目为有限个；③在一个周期内绝对可积，它就能展开为一个收敛的傅立叶级数.如图2所示，其输出的阶梯波是可以进行傅里叶分解的，分解如下：

f（t）=A02+∑

SymboleB@k=1Akmcos kω1t+φkAkmejφk=2T∫T0f（t）e-jkω1tdt （3）

式中：k=0，1，2，3，…；T为周期；A0/2为周期函数f（t）的恒定分量；Amcos （ω1t+φ1）称为1次谐波（或基波分量），其周期或频率与原周期函数f（t）相同；其他各项（k>1）统称为高次谐波.

假设图2中阶梯波的周期T=2π，并且有：

fα=-fα+T/2fT/2-α=fα（4）

Akmejφk=2T∫T0f（t）e-jkω1tdt=

2T∫T/20fte-jkω1tdt+∫TT/2fte-jkω1tdt=

21--1kT∫T/20fte-jkω1tdt （5）

当k为偶数时，Akmejφk=0，说明该阶梯波中不含偶次谐波分量；当k为奇数时，

Akmejφk=4T∫T/20f（t）e-jkω1tdt=

4T∫T/40f（t）e-jkω1tdt+∫T/2T/4f（t）e-jkω1tdt=

4T∫T/40f（t）e-jkω1t+e-jkπ-kω1tdt=

-8jT∫T/40f（t）sin （kω1t）dt=

-4jπ∫π/20f（t）sin （kω1t）dt （6）

令θi为第一个1/4周期内第i个阶梯波的电角度，s为第一个1/4周期内的阶梯波的个数，式（6）可化简为：

Akmejφk=-4jπ∑s-1i=1∫θi+1θifθisin （kω1t）dt+

∫π/2θsfθssin （kω1t）dt=4jkπ×

∑s-1i=1[fθicos （kω1θi+1）-

f（θi）cos （kw1θi）]-fθscos （kω1θs）（7）

Akm=4kπ（∑s-1i=1[f（θi）cos （kω1θi+1）-

f（θi）cos （kω1θi）]-f（θs）cos （kω1θs））（8）

式中：Akm为谐波幅值，即当k取不同数值时，就得到了不同次谐波幅值.

以16电平为例，设调制波ua=420 sinωt，假设用最近电平逼近时，触发脉冲是等间隔触发，从而可知：

θi+1-θi=π/16， i=1，3，5，7f（θi）=60iω1=2πf1=100π （9）

通过计算化简可得，Akm=（4×60）/kπ=240/kπ，忽略9次及9次以上奇数次谐波，可得3次谐波含量如下：

Ak3/Ak1+Ak3+Ak5+Ak7=19.89%（10）

2 谐波抑制策略

从式（10）可以看出，谐波含量较大，故而需要采取一定的措施来减小谐波含量.一般通过增加电感来进行滤波，这需要增大电感的体积并提高工程成本，本文采用广义积分器进行控制.

当给定的参考信号为常量或者直流信号时，控制器只要包含一个常规的积分器就能保证系统无稳态误差.当参考信号为具有某一频率的周期信号时，常规的积分器会导致系统存在稳态误差.广义积分器是一种针对非直流信号的积分器，采用广义积分器可以对非直流信号进行无稳态误差跟踪[11].当给定信号中包含了除频率ω外的其他正弦信号时，通过广义积分器本身的特性，只得到频率为ω的正弦信号的期望积分信号，而其他正弦信号的积分信号等于零，即广义积分器具有频率选择性.

本文将输出的电流经过陷波器提取出3次谐波，5次谐波，7次谐波，计算反相谐波电压并叠加到参考电压，从而有效抑制MMC的输出电流谐波.

MMC谐波抑制的整体控制框图如图3所示，以A相为例：

1）检测MMC A相输出电流Ia，获取其3次谐波分量Ia3oh，5次谐波分量Ia5oh，7次谐波分量Ia7oh；并将它们分别与0比较，经过广义分频 PI调节器得到A相抑制谐波的调制分量Uaref1，Uaref2，Uaref3.

Uaref1=0-Ia3oh×Kp1+Ki1×1/s （11）

Uaref2=0-Ia5oh×Kp2+Ki2×1/s（12）

Uaref3=0-Ia7oh×Kp3+Ki3×1/s （13）

式中：1/s为积分因子.

Kp1=0.8，Ki1=100

Kp2=0.6，Ki2=120

Kp3=1.2，Ki3=200

2）检测A相所有SM子模块的电容电压，并求和Uac，即

Uac=∑Ni=1Uci（14）

3）将Uac与其参考电压比较后，经过PI调节器得到该相環流参考值Iacirref；将Iacir与其参考值比较后，经过PI调节器得到稳压控制的输出量Uaref4，公式如下：

Iacirref=Uac-Uacref×Kp4+Ki4×1/s（15）

Uaref4=Iacirref-Iacir×Kp5+Ki5×1/s（16）

式中：Kp4=1.1；Ki4=85；Kp5=2；Ki5=200.

设模块化多电平变流器该相输出电压参考值为Uaref5，则A相总的调制电压Uaref为：

Uaref=Uaref1+Uaref2+Uaref3+Uaref4+Uaref5（17）

4）采用最近电平逼近进行调制，得到A相各个SM子模块的控制信号.B，C相控制方法类似.

3 仿真分析

3.1 参数设置

为了验证本文所提出的控制方法的可行性以及与传统控制方法相比所具有的优势，分别对系统的稳态过程和暂态过程进行了仿真.仿真参数如表2所示.

3.2 稳态结果

3.2.1 传统控制时稳态分析

仿真中MMC调制电压参考值设定为400 V，仿真结果如图4所示.从图4可以看出，A相输出电流基波幅值为19.05 A，输出电流畸变率为5.34%，桥臂环流振荡范围为3.1～5.1 A，根据傅里叶分解可知，直流分量为4.07 A，2次谐波分量为0.52 A，2次谐波含量为10.4%.子模块电容电压波动范围为97.3～102.9 V，交流纹波含量为2.8%.

3.2.2 本文所提方法稳态仿真分析

采用本文所提出的控制方法，得到的仿真波形如图5所示.由图5可知，A相输出电流基波幅值为19.3 A，输出电流畸变率为3.91%，桥臂环流振荡范围为3.7～5.3 A，根据傅里叶分解可知，直流分量为4.18 A， 2次谐波分量为0.39 A，2次谐波含量为7.8%.子模块电容电压波动范围为97.4～102.8 V，交流纹波含量为2.7%.与传统的控制方法相比，输出电流畸变率由5.34%降低到3.91%，2次谐波含量由10.4%下降到7.8%，子模块电容电压交流纹波含量基本保持不变.

3.3 暂态分析

3.3.1 传统控制时的暂态分析

仿真中，当系统达到稳定后，在0.1 s时， MMC调制电压突然由400 V降低到200 V， 采用传统的控制方法得到仿真结果如图6所示.从图6中可以看出，大约1个周波后系统达到新的稳定.达到新的稳定后，输出电流基波幅值由19.05 A变为8.694 A，总畸变率由5.34%变为13.57%，这是由于调制电压降低后，逆变器输出电平随之降低引起的.桥臂环流在-2～4 A之间振荡，根据傅里叶分解可知，直流分量为0.72 A， 2次谐波分量为0.22 A，2次谐波含量为14.7%，子模块电容电压在95.7～104.1 V之间波动，交流纹波含量为4.2%.

3.3.2 本文所提方法暂态仿真分析

采用本文所提出的控制方法，得到的波形如图7所示.从图7可以看出，大约1个周波，系统即可达到稳定，动态调节过程中基本无超调.达到新的稳态后，输出电流基波幅值由19.3 A变为9.346 A，总畸变率由3.91%变为11.88%，也是由于调制电压降低后，逆变器输出电平随之降低引起的.桥臂环流在-2～4.2 A之间震荡，根据傅里叶分解可知，直流分量为0.81 A， 2次谐波分量为0.19 A，2次谐波含量为12.7%，子模块电容电压在96.1～104.2 V之间波动，交流纹波含量为4.05%.与传统的控制方法相比，本文所提出的方法在暂态过程中，输出电流畸变率降低，子模块电容电压交流纹波含量和桥臂环流中的3次谐波含量基本没有变化.

4 实验验证

为了验证本文提出的控制方法的可行性，在实验室搭建了单相9电平的MMC原型样机，如图8所示.逆变器每个桥臂各8个SM子模块，桥臂电感为8.4 mH，直流侧电压为400 V，负载为一个可调电阻.实验中采集了子模块电容电压互感器的输出信号，互感器变比为26.4∶1.为了便于观察电压纹波，示波器仅仅显示了局部电压图.逆变器的每个子模块的额定工作电压为50 V，调制比给定为0.9，逆变器外接14.4 Ω的电阻负载.

图9为采用传统方法时MMC的输出电流波形图和采用本文所提方法时MMC的输出电流波形图，输出电流的谐波是由于MMC输出电平数较低产生的.图9中，输出电流波形图的纵坐标为5 A/格，对测量数据分析可知，图9（a）中输出电流基波幅值为11.2 A，总畸变率为7.63%，图9（b）中输出电流基波幅值为12.2 A，总畸变率为5.21%，由此可知，采用本文控制方法比传统控制方法输出电流畸变率低.

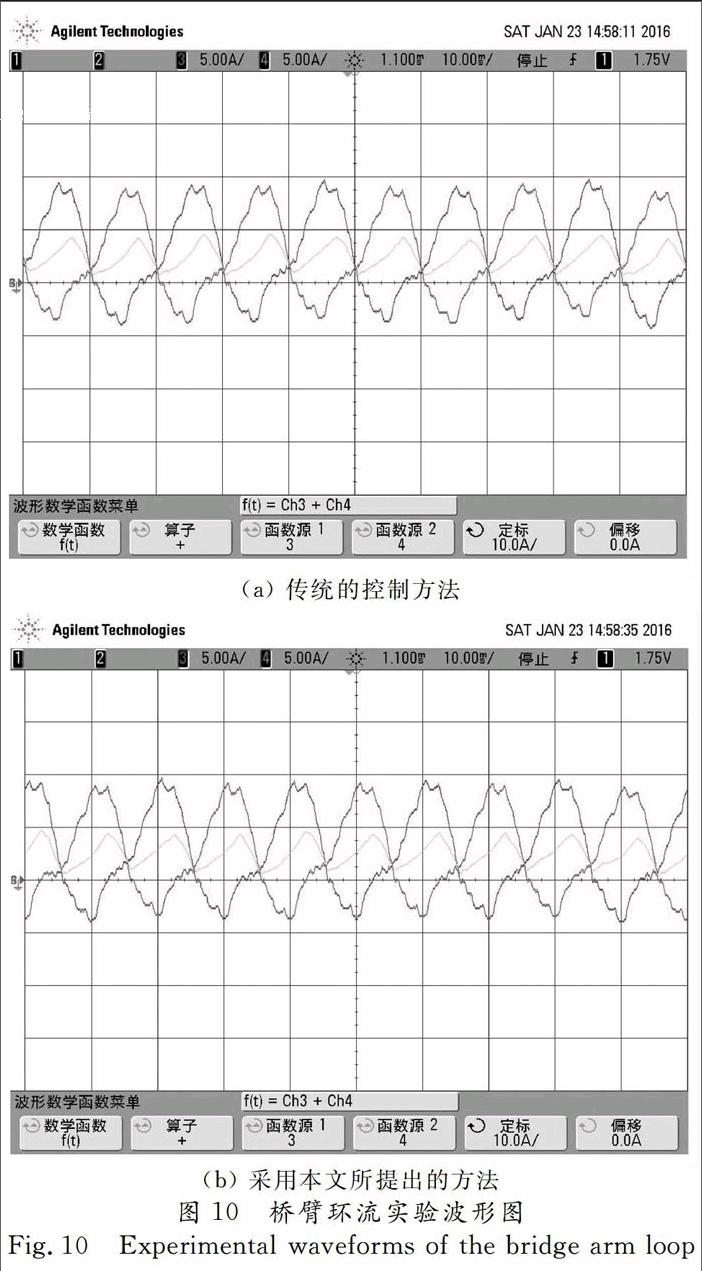
图10为采用传统方法时MMC的桥臂环流波形图和采用本文所提方法时MMC的桥臂环流波形图.图10中，上、下桥臂电流的纵坐标为5 A/格，由于桥臂环流的值为上下桥臂电流之和的二分之一，故桥臂环流定标为10 A/格.结合示波器对上下桥臂电流的求和操作得到桥臂环流波形，图10（a）中桥臂环流在1.1～4.93 A之间振荡；图10（b）中，桥臂环流在1.08～4.95 A之间振荡.由此可知，本文控制方法与传统控制方法相比，桥臂环流幅值变化不大.

图11为采用传统方法时子模块电容电压波形图和采用本文所提方法时子模块电容电压波形图.实验中采集了子模块电容电压互感器的输出信号，互感器变比为26.4∶1.为了便于观察电压纹波，示波器仅仅显示了局部电压图.子模块电容电压波形图中纵坐标为50 mV/大格，12.5 mV/小格，图11（a）中电容电压的波动范围占据了7小格（对应87.5 mV），由互感器变比可知，此时子模块电容电压的波动为2.31 V，故交流纹波含量为2.31%.图11（b）中电容电压的波动范围也占据7小格，说明采用本文的控制方法没有使子模块电容电压交流纹波含量变大.

5 结 论

本文提出了一种抑制模块化多电平变流器输出电流谐波的方法.该方法对输出电流进行分频提取后通过PI调节器得到反相谐波电压，最后将反相谐波电压叠加到调制电压上获得总的参考电压.本文提出的方法控制简单、易实现，与传统控制方法相比，谐波抑制效果明显，并且保证了模块化多电平变流器均压和稳压的正常运行.仿真及实验结果验证了本文所提出的控制方法的可行性和有效性.

参考文献

[1] 索之闻，李庚银，迟永宁，等.一种基于子模块混合型模块化多电平换流器的高压大功率DC/DC变换器[J].中国电机工程学报，2015，35（14）：3577-3585.

SUO Zhiwen， LI Gengyin， CHI Yongning， et al. A cell-hybrid modular multilevel converter based high-voltage high-power DC/DC converter[J].Proceedings of the CSEE，2015，35（14）： 3577-3585. （In Chinese）

[2] 張建坡，赵成勇，孙海峰，等. 模块化多电平换流器改进拓扑结构及其应用[J].电工技术学报，2014，29（8）：173-179.

ZHANG Jianpo， ZHAO Chengyong， SUN Haifeng， et al. Improved topology of modular multilevel converter and application[J]. Transactions of China Electrotechnical Society，2014， 29（8）： 173-179.（In Chinese）

[3] 韦延方，卫志农，孙国强，等. 一种新型的高压直流输电技术—MMC-HVDC[J]. 电力自动化设备，2012，7：1-9.

WEI Yanfang， WEI Zhinong， SUN Guoqiang， et al. New HVDC power transmission technology：MMC-HVDC[J]. Electric Power Automation Equipment，2012，7：1-9.（In Chinese）

[4] 赵成勇，胡静，翟晓萌，等. 模块化多电平换流器桥臂电抗器参数设计方法[J]. 电力系统自动化，2013，37（15）：89-94.

ZHAO Chengyong， HU Jing， ZHAI Xiaomeng， et al. A parameter design method of bridge arm reactor in modular multilevel converter [J]. Automation of Electric Power Systems，2013，37 （15）：89-94.（In Chinese）

[5] 赵昕，赵成勇，李广凯，等. 采用载波移相技术的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报，2011，31（21）：48-55.

ZHAO Xin， ZHAO Chengyong， LI Guangkai， et al. Submodule capacitance voltage balancing of modular multilevel converter based on carrier phase shifted SPWM technique[J]. Proceedings of the CSEE， 2011， 31（21）：48-55.（In Chinese）

[6] 李笑倩，宋强，刘文华，等. 采用载波移相调制的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报，2012，32（9）：49-55.

LI Xiaoqian， SONG Qiang， LIU Wenhua， et al. Voltage balancing control by using carrier phase-shift modulation of modular multilevel converters[J].Proceedings of the CSEE，2012，32（9）：49-55.（In Chinese）

[7] 公铮，伍小杰，王钊，等. 基于载波移相调制的模块化多电平变换器变频运行控制[J]. 中国电机工程学报， 2015， 35（11）：2822-2830.

GONG Zheng， WU Xiaojie， WANG Zhao， et al. Frequency operation control of modular multilevel converter based on carrier phase-shift modulation[J]. Proceedings of the CSEE， 2015， 35（11）：2822-2830. （In Chinese）

[8] 管敏渊，徐政，屠卿瑞，等. 模块化多电平换流器型直流输电的调制策略[J]. 电力系统自动化，2010，34（2）：48-52.

GUAN Minyuan， XU Zheng， TU Qingrui， et al. Nearest level modulation for modular multilevel converters in HVDC transmission[J]. Automation of Electric Power Systems，2010， 34（2）：48-52.（In Chinese）

[9] 管敏渊，徐政，潘伟勇，等. 最近电平逼近調制的基波谐波特性解析计算[J]. 高电压技术，2010，36（5）：1327-1332.

GUAN Minyuan，XU Zheng，PAN Weiyong， et al. Analytical calculation of fundamental wave and harmonic characteristics for nearest nearest level modulation[J]. High Voltage Engineering，2010，36（5）：1327-1332.（In Chinese）

[10]肖浩，高桂革，曾宪文，等. 改进的最近电平逼近调制策略在模块化多电平变流器中的应用[J]. 上海电机学院学报，2015，18（2）：70-76.

XIAO Hao ，GAO Guige，ZENG Xianwen， et al.Modified nearest level modulation for modular multilevel converter[J]. Journal of Shanghai Dianji University，2015，18（2）：70-76.（In Chinese）

[11]涂春鸣. 新型谐振阻抗型混合有源滤波器PITHAF研究[D]. 长沙：中南大学信息科学与工程学院，2003.

TU Chunming. Resonant impedance type hybrid active filter[D]. Changsha： College of Information Science and Engineering， Central South University，2003.（In Chinese）