模块化产品族的共享模块筛选方法

侯文彬+单春来+于野+张红哲

摘 要：针对在模块化平台中筛选共享变量的问题，受协同优化算法使用一致性约束函数对各子优化问题进行一致性统筹的启发，提出一种基于一致性约束的优化算法.在系统级优化中使用非支配排序的遗传算法NSGA-Ⅱ对该多目标优化问题进行求解后得到Pareto解集，利用模糊聚类算法对解集中的每组解进行综合性能的评价并选优，根据最终筛选出的最优解即可实现共享变量的筛选.相比以往常用的基于经验或灵敏度的方法，该方法更严格地在子学科优化中以车身性能为目标函数，在系统级优化中进行共享度的优化，并且可根据系统级优化结果筛选出局部共享变量.以SUV、两厢掀背车和三厢轿车为算例，使用该方法有效地筛选出3款车型的全局共享变量、局部共享变量和非共享变量，对该方法的可行性和有效性进行了验证.

关键词：一致性约束；协同优化；模糊聚类；模块化；产品族

中图分类号：U462.1 文献标志码：A

Selection Method of Sharing Modules for Modular Product Family

HOU Wenbin1，SHAN Chunlai1，YU Ye1，ZHANG Hongzhe2

（1. School of Automotive Engineering， Dalian University of Technology， Dalian 116024，China；

2. School of Mechanical Engineering， Dalian University of Technology， Dalian 116024，China）

Abstract：For sharing modules selection in the modular platform design， an algorithm based on constraints was proposed， which was inspired by Collaborative Optimization using the constraints to coordinate the System Level Optimization and Sub-system Level Optimization. In this algorithm， NSGA-Ⅱ was used in the System level to solve the Multidisciplinary Design Optimization problem， and a Pareto set was gotten. By using the fuzzy set theory to evaluate each equation in the Pareto set， the optimum solution was easily picked out， and the sharing modules selection was realized in this way. At last， this method was verified by using an application example constituted by involving a SUV， a hatchback， and a sedan.

Key words：consistency constraints； collaborative optimization； fuzzy set theory； modular； product family

随着汽车生产的全球化，制造水平的日益提高，以零部件超前发展为重心的模块化技术已经成为时下各大汽车制造厂商的核心技术，模块化产品族的设计制造方式也无疑是企业获得持续竞争力的最关键的内容[1-2].模块化设计作为新型产品平台构建的主要策略，以零部件标准化和多样化的方式提高了产品族内不同产品之间的零部件共享度并保证了产品的多变性[3].

Torstenfelt等[4]基于模块化平台的产品族中各类模块给出了相关定义.在将同产品族内产品的各零部件根据某些方法进行归类并划分为模块之后可以发现，某一产品除了使用个性化模块以突出自己的独特性能外，有相当一部分相似性很高的结构存在.在这些相似性结构中，有些模块可以不加任何改變就在同产品族下的所有产品之间进行通用，按以往的研究，称这些模块为共享模块；某些模块仅可以在一部分产品间使用，可将其定义为局部共享模块；此外还有些模块，虽然在各产品中具有较高的结构相似性，但其尺寸参数、材料参数等差异较大，不可以在不同产品间进行互换，这些模块则作为非共享模块存在.在模块化设计中，模块划分的主要任务就是确定模块的分割方式，并从这些相似性结构中筛选出共享模块和局部共享模块.

在以往的模块化研究中，各研究者和研究机构分别从不同的研究方向和角度推动了模块化研究的进程.如在模块划分的研究中，Simpson等[5-6]采用遗传算法，用多目标优化权衡产品族内各零部件的共性和特性后进行产品平台的模块化设计，提出可以通过划分市场来确定共享变量的比例因子进以确定共享结构和个性结构的参数化设计；Algeddawy等[7]采用层次聚类的方法对设计结构矩阵进行划分；Bhandare等[8]以产品族的成本模型为基础，根据设计变量对产品族整体性能的灵敏度确定共享变量以及非共享变量；Fellini等[9]进行了多年的研究，采用分级目标传递法（Analytical Target Cascading， ATC）对汽车平台下的车型进行了分级并提出了在性能函数约束下的平台一体化的选择方法.在优化方面，Torstenfelt等人[10]利用移动渐进线法（Method of Moving Asymptotes， MMA）对3个基于同一平台车型的白车身进行了优化，得到了较好的优化结果，然而他们所使用的内部软件TRINITAS 很难得到广泛应用，而且他们并未对如何选取平台共享模块进入深入研究；Ferguson等人[11]将同一产品族下的汽车视为可重构模型，提出利用多层次的多学科优化方法进行汽车设计，理论方法较简单，但是可以得到切实有效的应用.在平台整体性设计方面，Li等[12]将平台定义为参数化可调节的柔性平台，基于数据流分析提出一种使用设计结构矩阵和模糊聚类方法进行模块结构设计的方法； Liu等[13]通过网络分析法（Analytic Netwo Process， ANP）和目标规划方法对产品平台方案进行决策.

虽然在以往研究工作者的工作中，针对模块划分的方法以及同产品族内多车型同步优化都有很多较成熟的研究，但关于如何从划分后的模块中以最大共享度和最优化车身性能为依据筛选出共享模块和非共享模块的研究仍然较少.现阶段广泛使用的方法依然是在设计阶段依据经验或需要进行选取，通过不同部件的灵敏度最终确定优化变量[14-15].然而，这种方法较难定义足够明确的筛选标准，且并不能严格地以提高车身性能和模块共享度为优化的目标，得到的结果是否可以在这两方面达到最优尚且需要商榷，尤其注意的是，很难根据结果筛选出局部共享变量.针对这些问题，本文对协同优化算法的结构进行了调整，提出一种基于一致性约束函数和模糊集合理论的筛选共享变量的方法，可以较快捷地对产品族内的各类模块进行筛选.

1 协同优化算法

协同优化算法CO （Collaborative Optimization）是一种在工程上广泛应用的多学科优化方法（Multidisciplinary Design Optimization，MDO）.该算法在1994年由斯坦福大学的Kroo等人[16]首次提出.协同优化的主要思想是将复杂系统的优化问题分解成一个系统级优化问题和多个子系统级的学科优化问题，通过简化学科之间的关系来处理各学科之间的耦合.在进行子系统级的优化时，可以暂时不考虑其他学科的影响，只考虑当前子学科的约束.学科级优化的优化目标是使该学科的优化结果与系统级优化提供给该学科的目标值的差异达到最小，而各个学科级优化结果之间的不一致性由系统级优化进行协调，通过系统级优化和学科级优化之间多次迭代减小各学科之间的不一致性，最终得到一个符合学科间一致性要求的系统最优设计方案[17]，计算流程如图1所示.由于该方法对现代工程设计应用有良好的适应性，故该方法成为应用最普遍的多学科设计优化方法之一[18].

一般来说，协同优化是在系统级优化层次中优化每一子目标函数的同时综合考虑其他子目标函数的结果，使各子目标函数之间的优化结果能够一致.可以证明，如果变量的值一致则为最优解[19]，因此协同优化算法的系统级和学科级之间有较好的收敛性，很好地解决了许多实际中非线性优化及组合优化难题.例如，某标准工程优化问题的数学模型[20]如式（1）所示，f（x）代表优化目标函数，gu（x）代表问题中的不等式约束，hv（x）代表问题中的等式约束.

min f（x）

s.t. gu（x）≤0， u=1，2，…，m

hv（x）=0，v=1，2，…，n（1）

对于多目标优化问题，f（x）可以是多个函数；对于大于等于0的不等式约束，可以在gu（x）前添加负号转化为标准形式，而不等式约束和等式约束总可以相互转化，如通过采用式（2）进行相互转换.

gu（x）+a2=0， a≥0

hv（x）-b2≤0， b≥0（2）

在实际工程应用中，目标函数f（x）以及约束gu（x），hv（x）往往比较复杂，对于复杂约束或复杂目标等问题，可以根据协同优化的思想，将式（1）分解为相对简单的一个系统级优化和多个子系统级学科优化两个层次.

1）系统级优化.

min f = f（z）

s.t.

Ji（z，p）=∑n1j=1zij-pij2=0

i=1，2，…，N（3）

2）学科级优化（第i个学科）.

min Ji（x，p）=∑n1j=1xij-pij2

s.t. gid（x） ≤0， hie（x）=0 （4）

式中：目标函数f为系统级目标函数，通常是原优化问题的优化目标并根据实际加以分解[21].原優化问题式（1）中的优化变量x分派到不同的学科式（4）中进行优化，而不同学科中的相同变量x间往往存在冲突，因而将其传递回系统级优化式（3）中作为统筹变量p进行一致性优化，优化后得到的z即为系统级的优化结果，传递回学科级优化中进行下次迭代.J作为学科级优化的优化目标和系统级优化的约束，保证系统级和学科级之间的一致性，即为一致性约束，一般采用二范数进行定义.系统级与学科级之间的关系为：

pij=x*ij， qij=zij（5）

2 多级一致性约束优化算法

2.1 提出背景

对同一产品族内的不同车型进行可共享变量的筛选时，除了要最大化车身部件共享度（即共享的模块越多越好）外，还要综合考虑到各车型的质量、弯曲刚度和扭转刚度等各方面的性能，同时要兼顾产品平台的整体优化结果和各个车型的单独优化结果，才能保证在产品族内最大化共享度的同时提升车辆的性能.通过选取可共享的变量进而提高共享度的同时，不能降低各车型原有的性能.以往的方法大多是根据设计者的经验或车型定位的要求选取，或者根据对各部件的尺寸变量的灵敏度大小进行选取（对车身性能灵敏度高的部件作为平台优化变量优先设计，灵敏度低的则作为单车优化变量）.但这种方法很明显不以共享度或车身性能为目标函数，不能严格保证共享度的最大化或车身性能的最优化，且难以对局部共享变量进行筛选.针对这样的缺点，受协同优化方法中使用一致性约束函数统筹各子系统之间以及子系统与系统级之间关系的启发，对协同优化方法的结构进行调整，得到一种以共享度和车身性能为目标函数的基于一致性约束函数的优化方法.

虽然对产品族的优化需要以平台整体性能为最终优化目标，但依然需要兼顾到所有车型，因而可将各单个车型作为子学科，在子学科内以当前车型的性能为优化目标函数，即认为当所有车型性能都达到最优时，该模块化平台达到最优.由于在协同优化算法的整体结构下，各子学科优化问题具有良好的学科自治性，同时在自变量之间不存在严重耦合的前提下，系统级优化很容易对各子学科进行协调统一，因而该算法结构对产品族优化问题具有很好的适应性.

2.2 算法结构

将筛选共享变量的问题划分为系统级优化和子系统级优化两个层次，设置所有通用性结构的尺寸及属性等参数为初始参数，从中进行共享模块和局部共享模块的筛选.由前文可知，一致性约束的作用是用来统筹系统级和子系统级之间的变量一致性关系，在协同优化算法中通过约束其为零或小于某一小值使各子优化问题达到协同.如果将该约束转变为目标函数并求其可能达到的最小值，则可以通过优化后的结果评价对应自变量的差异程度：如果差异值很小，则该变量对应的模块可以作为共享模块在各车型之间进行通用，如果差异值较大，则对应的模块应作为个性化模块进行单独设计制造.

将协同优化算法流程调整为多级一致性约束优化算法，如图2所示.将协同优化算法中的一致性约束J作为系统级优化目标进行优化，并在得到最终结果后根据值的大小进行筛选.在优化过程中系统级变量p的取值范围应保持在对应部件的可制造尺寸范围内，可以在保证可制造性的同时，避免系统最优点在约束边界上时优化算法往往会收敛于一个不满足子学科约束的最优值的问题.

在子系统级优化中，每个子问题都对应一种车型的一种或几种工况，以评价车身性能的函数f（x）为优化目标，该车型在各工况下的相应约束为约束.将各子系统优化后的自变量x值传递回系统级优化进行一致性统筹，得到的系统级优化解z统一代回各子系统内进行下一轮迭代，直至最后系统级优化收敛.

很多研究已经表明，在协同优化算法中，由于引入了一致性约束，会导致原问题的非线性程度加强，且由于变量之间存在耦合，一致性约束条件通常很难满足，因而会引起很多巨大的困难且计算不易收敛，即由于某一自变量在不同子学科中进行优化时的优化方向相反导致公式（5）在计算迭代的过程中发散[22-23].但对于本文所要解决的筛选共享变量的问题，由于同产品族下的各车型之间存在基础框架的相似性和大部分尺寸的相近性，不会导致结果出现特别严重的耦合现象，即很少会出现某车型下某一变量的变化会优化该车型的性能却导致另一车型性能变差的情况，因而该算法计算迅速，不会出现收敛性方面的困难.如在对某产品族内三款不同车型约束其弯曲或扭转刚度后对白车身质量进行轻量化优化时，选取白车身侧围构件为主要研究对象，其中相似性结构的14根梁结构的灵敏度几乎完全一致，具体数值如表1所示.

由灵敏度的一致性可以判断，在以这14根梁为优化变量，以刚度为约束函数，质量为目标函数进行优化时，不会有导致计算不收敛的耦合现象出现.后文算例仍以这三款车型为例，具体模型以及梁结构的编号可详见本文第4节.另外，由于协同优化方法用一致性约束“强制”使各子学科优化问题内对应的优化变量一致，即“强”令（zij-pij）2等于零或小于某一微小值，容易造成计算的困难，而本文进行调整之后的方法将一致性约束函数更改为优化目标函数，根据优化后的结果对各子学科优化问题内对应的优化变量的一致性进行判断，约束较协同优化算法更“弱”，因而不会有协同优化问题中常见的计算困难和收敛困难.

本文提出的多级一致性优化算法在几何意义上可用图3表示.工程中的优化问题大多为多目标优化问题，该类问题的解为对应优化空间中的一个解集，构成一个Pareto曲线前沿.如图3所示，在A，B两个不同产品以相同的性能为优化目标函数（如最大化刚度、最小化质量等）进行优化后，产品A和产品B各自存在一条Pareto前沿曲线，可根据对产品定位各自对性能需求的权重占比从曲线上进行选择.如果在性能定位所允许的区间内，产品A和产品B对应的变量1和变量2存在完全一致或相差不多的区间，即如图3中放大的虚线框内所示的差值为零的点以及差值放松到某一微小值的点，则可认为在该区间内该变量所代表的零部件可以在这2个产品之间进行通用，该变量即为共享变量.本文提出的方法就是用来寻找所有自变量所对应的这一放大区间，通过系统级优化的结果判断该区间是否存在.

3 基于模糊集合理论的解集选优

对于多层次优化算法，系统级优化应对各子系统优化进行统筹[24]，而传统的基于梯度算法要求目标函数和约束函数总是光滑的，在系统级优化问题中并非总是满足，会导致算法可靠性差.研究表明，进化算法仅需适应度函数值进行操作，不需要求导，不要求设计空间连续，有较好的全局搜索性，最为适合[25].本文所述方法使用改进的非支配排序的遗传算法NSGA-Ⅱ进行求解.

使用NSGA-Ⅱ算法对多目標优化问题进行求解，所得到的并非是单个确定解，而是一条前沿曲线上的Pareto解集，因而需要从该解集中根据需要选择一个确定的最优解作为最终结果[26].前文所述用来筛选变量的算法中，目标函数及自变量数量较多，人工依次选优缺少依据且工作量较大.本文采用一种基于模糊集合理论的Pareto解集选优方法[23]，从而迅速得到最优解.

4 算例验证

4.1 模型建立及校验

为验证上述方法的有效性，本文以同一产品平台下的SUV、两厢掀背车和三厢轿车三款车型的白车身侧围为研究对象进行模块筛选.由于为同一产品族内的车型，因而在结构上有较大相似性，该算例中的3个车型的除尾部不同、SUV在纵向高度上略高、两厢掀背车和三厢轿车的发动机舱略长外，其他结构的尺寸基本一致.计算模型采用梁单元模型，由某车型的详细模型简化而来，如图4所示.

为确保计算结果的正确性，对简化的梁单元模型进行对标.分别计算详细模型（壳单元模型）和简化模型的弯曲刚度、扭转刚度和低阶模态，加载方式如图5所示.其中，梁单元模型单元尺寸30 mm，网格数量4 000个，详细模型使用壳单元尺寸10 mm，网格数量32万个.弯曲载荷为左右各1 000 N，扭转载荷为1 800 N，计算后的对比结果如表2所示.其中，在概念设计阶段，一般以车身梁结构确定车身结构的低阶模态参数等指标.在本次模拟中，为了避免简化模型中板结构所产生的局部模态，所以在简化模型的基础上去掉板单元进行模拟，由于去掉了板单元，所以主要只针对整体模态进行了对比.由表3中结果可以看出，详细模型和概念模型的计算结果趋势一致且误差在接受范围内.

4.2 共享变量筛选

从以上3个车型的车身侧围筛选出可共享的子部件，侧围结构如图6所示.按照概念设计阶段的设计方法，该产品族车型的车身侧围可以由14根梁结构构成，每根梁均可简化为等截面的矩形梁，以两个边的长度a，b和厚度t1， t2为主要变量.在实际制造过程中，虽然某些部件的厚度尺寸不同，但只需更换原材料和不同型号的板材而模具可以通用，因此t1和t2不作为系统变量进行筛选，只作为子学科优化变量参与车身性能的优化.由于建模时车身特征的不同，在进行筛选之前就可以确定9和11只可能为两厢掀背车和三厢轿车之间的局部共享变量，而不能与SUV进行共享.

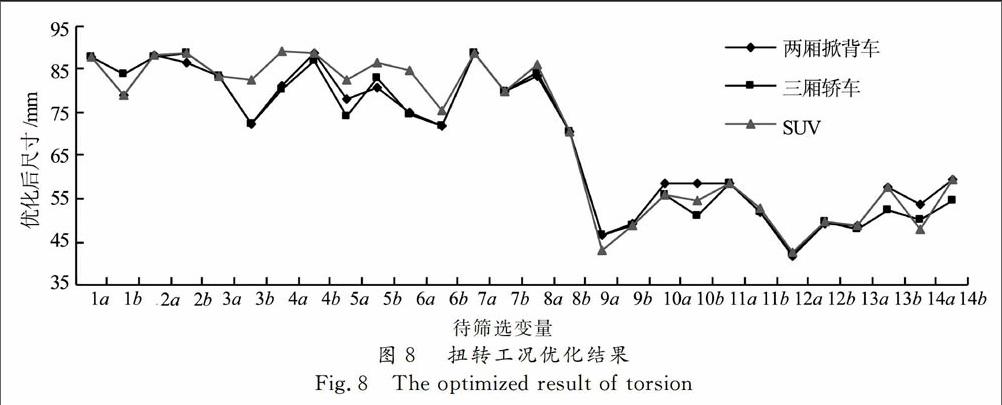
针对弯曲工况和扭转工况分别使用第2节所述方法进行优化，在遗传算法中定义种群规模200个，迭代200代，交叉概率0.8，突变概率0.005，以车身变形时的最大变形量以及车身的质量作为车身性能的优化目标函数，按照第3节所述方法从中选优，最终得到2个工况下不同梁的a和b的优化结果分别如图7和图8所示.图中横坐标为优化变量，如3b代表图6中简化梁3的b尺寸.由图7中结果可以进行变量筛选，如3个车型所对应的1b变量结果重合，则应对应为共享变量；SUV的6a变量与另2车型相差较多，对应为两厢掀背车和三厢轿车的局部共享变量.图8中3个车型的5a变量结果离散，对应为非共享变量.

4.3 筛选结果

从图7和图8所示的结果中可以进行最终筛选，最终共享情况由2个工况的筛选结果取交集，如表3所示.在本算例中将侧围的每个梁结构部件均视为一个可以进行单独制造并根据需要进行共享的模块，当某一模块的2个设计变量a，b均为共享变量时，则将该梁作为共享模块.

为简明起见，在图9中用数字标明分块制造的部件（即模块），并在表3中对这些模块进行共享情况的说明.表3中，h-s代表两厢掀背车和三厢轿车的侧围之间的共享部件；h-v代表两厢掀背车和SUV的侧围之间的共享部件；s-v代表三厢轿车和SUV之间的共享部件.在使用以往常用的基于灵敏度的筛选方式时，较易根据各梁的灵敏度的大小进行排序得到全局共享结构为1，2，5，7，8，然而对于局部共享变量很难进行筛选，往往只能依据经验进行判断，甚至直接定义为非共享变量.

5 结 论

本文根据传统的协同优化算法进行了结构上的调整，得到一种多级一致性约束优化算法，使用改进的非支配排序遗传算法NSGA-Ⅱ在系统级进行统筹，对迭代收敛后得到的Pareto解集进行基于模糊集合理论的解集选优，得到最优解.将该方法应用在汽车模块化平台产品族的共享变量筛选上，其意义是与最优解相对应的模块部件在不同车型之间可以进行通用共享，成为共享模块.相对于以往所使用的基于灵敏度筛选共享变量的方法，本文提出的方法在子学科优化中进行车身性能的优化，在系统级优化中进行共享度的最大化，除了能够筛选出全局共享变量外还能够确定局部共享变量，能够得到更加明确的结果.本算法将一致性约束函数作为系统级的最终优化目标函数，避免了协同优化算法中的计算困难、不易收敛等问题.

参考文献

[1] 吴永明，侯亮，祝青园，等.基于产品族的核心模块严谨分析与评价方法[J].农业机械学报， 2014， 45（4）：294-303.

WU Yongming， HOU Liang， ZHU Qingyuan， et al. Evolution analysis and evaluation for core module based on product family[J]. Transactions of the Chinese Society for Agricultural Machinery， 2014， 45（4）：294-303.（In Chinese）

[2] 王毅，范保鲜.新产品开发中的动态平台战略[J]. 科技管理， 2004，25（4）：97-103.

WANG Yi， FAN Baoxian. Dynamic platform strategy in new product development[J]. Science Research Management， 2004，25（4）：97-103.（In Chinese）

[3] 魏巍，梁赫，許少鹏.基于人工免疫改进算法的文件产品平台模块划分[J].计算机集成制造系统，2015，21（4）：885-893.

WEI Wei， LIANG He， XU Shaopeng. Module division method of robust product platform based on improved artificial immune algorithms[J].Computer Integrated Manufacturing Systems， 2015， 21（4）：885-893.（In Chinese）

[4] TORSTENFELT B， KLARBRING A. Conceptual optimal design of modular car product families using simultaneous size， shape and topology optimization[J]. Finite Elements in Analysis and Design， 2007， 43：1050-1061.

[5] SIMPSON T W， DSOUZA B. Assessing variable levels of platform commonality within a product family using a multi-objective genetic algorithm[C]//Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. Reston Va，USA： AIAA，2002，9：1-10.

[6] JIAO J， SIMPSON T W， SIDDIQUE Z.Product family design and platform-based product development： a state of the art review[J]. Journal of Intelligent Manufacturing，2007，18（1）：5-29.

[7] ALGEDDAWY T， ELMARAGHY H. Optimum granularity level of modular product design architecture[J].CIRP Annals-Manufacturing Technology，2013，62（1）：151-154.

[8] BHANDARE S，ALLADA V.Scalable product family design： case study of axial piston pumps [J].International Journal of Production Research，2009， 47（3）： 585-620.

[9] FELLINI R， KOKKOLARAS M， PAPALAMBROS P.Quantitative platform selection in optimal design of product families， with application to automotive engine design[J].Journal of Engineering Design，2006， 17（5）：429-446.

[10]TORSTENFELT B， KLARBRING A.Conceptual optimal design of modular car product families using simultaneous size， shape and topology optimization [J].Finite Elements in Analysis and Design，2007，43：1050-1061.

[11]FERGUSON S， LEWIS K.Designing a family of reconfigurable vehicles using multilevel multidisciplinary design optimization[J].Structural Multidisciplinary Optimization，2009，39（2）：171-186.

[12]LI Zhongkai， CHENG Zhihong， FENG Yixiong， et al. An integrated method for flexible platform modular architecture design[J].Journal of Engineering Design，2013，24（1）：25-44.

[13]LIU E， HSIAO S W. A decision support system for product family design[J]. Information Sciences，2014，281（10）：113-127.

[14]袁焕泉，陈东，张琪，等.基于平台模块化的汽车车身前期优化技术研究[J]. 机电工程， 2015， 32（9）： 1181-1185.

YUAN Huanquan， CHEN Dong， ZHANG Qi， et al. Previous optimization of car body based on platform and modularization[J]. Journal of Mechanical & Electrical Engineering， 2015， 32（9）： 1181-1185.（In Chinese）

[15]魏巍，梁赫，许少鹏.参数化产品族递进式优化设计方法[J]. 北京航空航天大学学报， 2015， 41（9）： 1600-1607.

WEI Wei，LIANG He，XU Shaopeng.Parametric product family progressive optimization design approach[J].Journal of Beijing University of Aeronautics and Astronautics， 2015， 41（9）： 1600-1607.（In Chinese）

[16]KROO I， ALTUS S，SOBIESZCZANSKI-SOBIESKI J，et al.Multidisciplinary optimization methods for aircraft preliminary design[C]//American Institute of Aeronautics and Astronautics，1994，4325：697-707.

[17]IAN P S.Multidisciplinary design using collaborative optimization[D].Palo Alto：Stanford University，1998.

[18]劉克龙，姚卫星，余雄庆.几种新型多学科设计优化算法及比较[J]. 计算机集成制造系统，2007，13（2）：209-216.

LIU Kelong， YAO Weixing， YU Xiongqing. Some new algorithms for multidisciplinary design optimization and their comparison[J]. Computer Integrated Manufacturing Systems， 2007， 13（2）： 209-216.（In Chinese）

[19]KROO I， MANNING V. Collaborative optimization： status and directions[C]//8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Long Beach， CA： AIAA，2000：AIAA-2000-4721.

[20]陳俊岭，阳荣昌，马人乐.大型风电机组组合式塔架结构优化设计[J].湖南大学学报：自然科学版，2015，42（5）：29-35.

CHEN Junling， YANG Rongchang， MA Renle. Structural design optimization of a composite tower for large wind turbine systems[J]. Journal of Hunan University：Natural Sciences，2015，42（5）：29-35.（In Chinese）

[21]魏峰涛，宋俐，李言，等.改进的多学科协同优化方法[J].计算机集成制造系统，2013，19（9）：2116-2122.

WEI Fengtao， SONG Li， LI Yan， et al. Improved multidisciplinary collaborative optimization method[J]. Computer Integrated Manufacturing Systems，2013，19（9）：2116-2122.（In Chinese）

[22]杨希祥，杨慧欣，江振宇，等.基于支持向量回归机和粒子群算法的改进协同优化方法[J]. 湖南大学学报：自然科学版， 2011，38（3）： 34-39.

YANG Xixiang， YANG Huixin， JIANG Zhenyu，et al. Improved collaborative optimization based on support vector regression and particle swarm optimization[J].Journal of Hunan University：Natural Sciences，2011，28（3）：34-39.（In Chinese）

[23]朱崎峰，宋保维.一种快速收敛的多学科协同优化方法[J].计算机集成制造系统，2014，20（5）：1013-1019.

ZHU Qifeng， SONG Baowei. Multidisciplinary collaborative optimization with fast convergence characteristic[J].Computer Integrated Manufacturing Systems，2014，20（5）：1013-1019.（In Chinese）

[24]LIN J G. Analysis and enhancement of collaborative optimization for multidisciplinary design[J]. American Institute of Aeronautics and Astronautics Journal，2004，42（2）：348-360.

[25]任毅如，张田田，曾令斌.基于遗传算法的潮流能水轮机翼型优化设计[J].湖南大学学报：自然科学版，2015，42（10）：59-64.

REN Yiru，ZHANG Tiantian， ZENG Lingbin.Tidal turbine hydrofoil design method based on genetic algorithm[J]. Journal of Hunan University：Natural Sciences，2015，42（10）：59-64.（In Chinese）

[26]ABIDO M A.Multi-objective evolutionary algorithms for electric power dispatch problem[J].IEEE Transactions on Evolutionary Computation， 2006， 10（3）：315-329.