基于Tikhonov正则化与模型减缩技术的虚拟迭代载荷反求

张邦基+周守玉+谢庆喜+张农

摘 要：将模型减缩技术应用于动态响应的求解，基于Tikhonov正则化载荷反求方法， 在迭代过程逐步修正载荷信号，使系统的响应逼近期望响应信号，最终精确反求出载荷信号.算例表明，该方法相对于传统Tikhonov方法，既保留了良好抗噪特点，同时又提高了峰值载荷处的反求精度，从而使得整体反求精度更高.

关键词：载荷反求；正则化；虚拟减缩；迭代方法

中图分类号：TP391.9 文献标志码：A

Load Identification of Virtual Iteration Based

on Tikhonov Regularization and Model Reduction

ZHANG Bangji，ZHOU Shouyu， XIE Qingxi，ZHANG Nong

（State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University， Changsha 410082， China）

Abstract： The model reduction technique was applied to solve the dynamic response. In order to make the system show the actual responses of the expected signals， the iteration procedure was then used to modify the load signals based on Tikhonov regularization load identification. Furthermore， the accuracy of the load signals was identified. The comparison of the proposed method with the traditional Tikhonov method shows that the proposed method can retain a good anti-noise characteristic， and improve the precision of load identification. The accuracy of the load identification by the proposed method is much higher than that of the traditional method.

Key words：load identification； regularization； virtual reduction； iterative methods

工程振动问题备受关注，结构动态载荷的精确获取可为工程结构的振动分析、疲劳分析等提供基础，然而因经济性或技术条件的限制，许多情况下载荷难以通过直接测量的方式获取，如汽车车身所受的激振力、轮船行驶时受到的波浪式冲击载荷等.因此利用载荷反求方法间接获取激振载荷具有重要意义.

载荷反求是通过系统响应和振动特性来反求结构所受载荷，是动力学第二类反问题[1].国内外学者针对动态载荷反求的理论和技术研究做了很多工作[2-4].传统的反求方法有时域法与频域法两大类[5]，随着计算机技术的发展，遗传算法[6]、神经网络[7]等新方法被应用于载荷反求领域.Kim等人[8]利用结构动力学关系构建载荷反求动力学方程，通过频响函数求逆法进行载荷反求，用奇异值分解法（SVD）改善频响函数求逆过程中的矩阵病态问题；Choi等人[9-10]运用最小二乘的Tikhonov正则化方法解决矩阵的病态问题，在提高载荷反求结果稳定性与抗干扰性方面效果良好，并对比分析了不同正则化参数选择方法对载荷反求精度的影响.国内在正则化反求法方面做了很多研究[11-13]，其中应用较广的是Tikhonov正则化反求法.郭荣等[14]综合运用Tikhonov正则化与奇异值分解的反求方法，有效提高了结构载荷反求精度.

然而Tikhonov等正则化反求法存在其自身的缺陷，由于该方法对反求载荷有平滑的作用，导致在响应测试噪声水平较高，或者系统线性程度不高的情况下，在反求信号的峰值处将很难得到较好结果[12].对此，结合文献[15]中室内试验台架驱动文件生成方法，提出新的载荷反求方法.其基本流程是，将Tikhonov正则化所反求的载荷重新激励系统，将获得的响应与真实期望响应对比，通过误差反馈补偿来逐步修正Tikhonov正则化反求法所得到的载荷信号，以提高在载荷峰值处的反求精度.考虑到在实际工程中，所研究的对象往往是复杂结构仿真模型，迭代中頻繁的正向求解过程相当耗时，甚至导致反求过程难以实现.对此，本文结合模型减缩技术，对大型有限元结构进行降阶处理，得到规模较小的等价模型，在保证响应计算精度的同时，极大缩短正问题的求解时间，提高计算效率.

1 虚拟迭代载荷反求原理

1.1 Tikhonov正则化理论

对于线性系统，在待反求载荷f（t）的作用下，系统的响应可以由单位脉冲响应函数与动态载荷的卷积分形式表示为：

y（x，t）=∫t0G（x，t-t）f（t）dt（1）

式中：y（x，t）为结构测点x处的响应，可以是位移、速度、加速度等；f（t）为载荷的时间历程；G（x，t）是相应的载荷作用点到响应点的Green函数，即单位脉冲响应.

考虑零初始条件系统，可将式（1）中的卷积分在时域内进行n个等间隔时间点离散，可化为一组线性方程组：

1.2 迭代反求算法

當线性时不变系统响应噪声水平不高时，采用最优正则化参数的Tikhonov方法可较精确地反求激励载荷，但是当系统响应噪声水平较高时，即使是最优的正则化参数，也难以平衡解的逼近性与稳定性这对矛盾；且在工程实际中，系统的各个环节，如汽车的衬垫等连接部件，在一定程度上都存在非线性因素，导致反求难度增大.对此，采用迭代的方法，根据响应误差反馈补偿，逐步修正所求载荷信号，使其达到要求[16].

首先，对一个已知系统，其响应信号Yδ，由上述Tikhonov正则化方法反求，计算出初始载荷信号为：

1.3 减缩技术

载荷的迭代反求过程，需要反复计算仿真系统的动响应，仿真系统通常用有限元的方式表达.但对于有限元模型，通常网格越密仿真精度越高，但密集的网格会导致响应求解时间增长，尤其在反复迭代计算过程中，正问题的求解时间过长是影响迭代的重要因素.对此，采用模型减缩技术，对原始有限元模型进行降阶等效，再对降阶模型进行迭代响应计算，从而解决计算精度与计算效率之间的矛盾.本文采用的减缩方法是IRS[19]方法.

IRS 减缩方法是一种基于 Guyan静力减缩法并考虑惯性力影响的改进方法.系统的运动方程可以表示为：

1.4 迭代收敛条件

上述Tikhonov迭代正则化算法可用流程框图表示，如图1所示.

2 数值算例

为了验证上述迭代法对Tikhonov正则化反求结果的优化作用，以及模型减缩技术对迭代效率改善的正确性与有效性，下面给出几种不同载荷形式的算例进行仿真对比分析.选用一块带约束的平板，在ABAQUS中建立如图2所示的有限元模型，平板一边两端用螺栓夹紧固定，模型中平板的弹性模量为210 GPa，密度为7.85 g/cm3，厚度为4 mm，边长为500 mm.

2.1 模型减缩应用及结果分析

为提高响应计算速度以及迭代效率，对该模型进行减缩降阶，在确保模型精度不受影响的情况下，用近似的低阶模型代替原来复杂的高阶系统模型来进行迭代反求.对该有限元模型，质量矩阵和刚度矩阵通过ABAQUS被直接导出，在模型上选取包括激振点与拾振点在内共 176个节点，用IRS减缩法在 MATLAB 中对平板模型进行模型减缩，并用模态置信度（MAC值）分析减缩前后模型模态振型吻合程度，验证该减缩模型的精度[20].

2.1.1 减缩前后振型对比

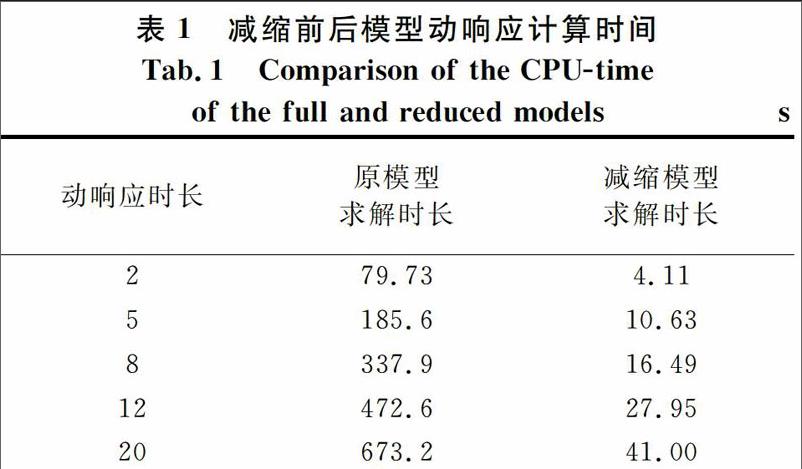
2.1.2 动响应计算效率分析

在载荷反求过程中往往需要反复多次求取系统响应，因此动响应计算效率是衡量反求实际效果的重要标准.分别对算例原模型、IRS减缩模型求动态响应，比较相同时间历程的动态响应所消耗实际CPU时间，结果如图4所示.

由此可见，相比于原模型，IRS减缩模型大大减少了动响应计算时间，因此，模型减缩很大程度上提高了计算效率，所需计算响应时间历程越长，效果越明显.在本文数十次迭代计算动态响应过程中，IRS模型减缩技术的应用将极大地提高迭代计算响应效率.

2.2 载荷反求对比分析

在板面节点308#施加垂直于板面的单位载荷，选取响应节点62#垂直板面方向速度作为响应（如图2所示）.首先计算载荷点到响应节点对应的Green函数；再以不同形式载荷下的响应，进行载荷反求；最后对仿真得到的响应数据加入一定水平的随机噪声来模拟测试误差.此时带噪声的速度响应可用下式来表示：

式中：Y（t）为仿真得到的速度响应；std（Y（t））为速度响应Y（t）的标准差；lnoise为噪声水平的百分数；rand（-1，1）是区间-1，1的随机数[12].

在速度响应中加入15%的模拟噪声，首先用传统的Tikhonov正则化方法进行载荷反求，以L曲线法确定最优正则化参数，得到待求载荷，计算反求精度；再以此反求载荷，作为初始激励载荷，用上述虚拟迭代方法修正载荷信号，进行反求优化，以达到精度要求；最后对比优化前后载荷反求精度.

选用不同频率、不同幅值周期正弦、正弦扫频（10～100 Hz）、三角波以及随机激励等形式的激振力激振进行载荷反求，反求结果如图5-图9所示.

由图5-图9可以看出，对不同形式的激励，在一定噪声水平情况下，传统的L曲线法确定最优参数的Tikhonov正则化方法能够很好地抑制噪声对反求结果的干扰，具有很强的稳健性.但在载荷峰值处，反求误差较大，反求整体精度受影响，这主要是由于正则化方法对反求载荷有平滑的作用，使得该方法在载荷峰值难以得到准确的反求结果.Tikhonov正则化方法对这几种载荷反求的加权误差为8.0%左右.而本文提出的迭代Tikhonov正则化方法不仅能够继承传统正则化方法反求结果稳健性的优点，同时还可以改善其在载荷峰值处反求结果，提高反求精度，反求结果加权误差最低可降至2.0%.迭代Tikhonov正则化方法无论对确定信号还是随机载荷激励都有很好的反求精度，且对如图9所示中的高频载荷段迭代反求也有很高的精度.

3 结 论

本文在传统Tikhonov正则化反求方法的基础上，提出了一种新的迭代改进方案.结合有限元算例和模型减缩技术，分别采用传统Tikhonov方法和本文迭代方法对三角、正弦以及随机载荷等激励进行载荷反求.结果表明：

1）本文提出的基于Tikhonov正则化迭代反求方法不仅能够继承传统Tikhonov正则化反求法有效抑制噪声的特点，同时还可以提高其在峰值载荷处的反求精度，整体反求精度高；

2）应用模型减缩技术可以提高动响应求解效率，有助于载荷反求迭代过程的开展，最终又快又好的求得激励载荷.

参考文献

[1] MARCHUK G I. Methods of numerical mathematics[M]. Berlin： Springer-Verlag， 1975： 16-18.

[2] 孫兴盛，刘杰，丁飞，等.基于矩阵摄动的随机结构动态载荷识别技术[J].机械工程学报，2014， 50（13）：148-156.

SUN Xingcheng， LIU Jie， DING Fei， et al. Identification method of dynamic loads for stochastic structures based on matrix perturbation theory[J]. Journal of Mechanical Engineering， 2014， 50（13）： 148-156.（In Chinese）

[3] 彭凡，马庆镇，肖健，等.整体平动自由结构载荷时域识别技术研究[J].振动与冲击，2016， 35（6）：91-95.

PENG Fan， MA Qingzhen， XIAO Jian， et al. Load identification technique in time domain for free structures with overall translation[J]. Journal of Vibration and Shock， 2016， 35（6）： 91-95.（In Chinese）

[4] SANCHEZ J， BENAROYA H. Review of force reconstruction techniques[J]. Journal of Sound and Vibration， 2014， 333（14）： 2999-3018.

[5] 胡寅寅，率志君，李玩幽，等.设备载荷识别与激励源特性的研究现状[J].噪声与振动控制，2011（4）：1-5.

HU Yinyin， LV Zhijun， LI Wanyou， et al. Status QUO of study on machine，s load identification technique[J]. Noise and Vibration Control， 2011（4）： 1-5.（In Chinese）

[6] 刘杰，许灿，李凡，等.基于λ-PDF 和一次二阶矩的不确定性反求方法[J].机械工程学报，2015， 51（20）：135-143.

LIU Jie， XU Can， LI Fan， et al. Uncertain inverse method based on λ-PDF and first order second moment[J]. Journal of Mechanical Engineering， 2015， 51（20）： 135-143.（In Chinese）

[7] 莫旭辉，韩旭，钟志华.基于渐近神经网络的汽车前轮定位参数反求[J].湖南大学学报：自然科学版，2008， 35（6）：18-22.

MO Xuhui， HAN Xu， ZHONG Zhihua. Identification of front wheel alignment based on the progressive neutral NETW ORK method[J]. Journal of Hunan University：Natural Sciences， 2008， 35（6）： 18-22.（In Chinese）

[8] KIM Y C， NELSON P A. Optimal regularisation for acoustic source reconstruction by inverse methods[J]. Journal of Sound and Vibration， 2004， 275（3）： 463-487.

[9] CHOI H G， THITE A N， THOMPSON D J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J]. Journal of Sound and Vibration， 2007， 304（3/5）： 894-917.

[10]CHOI H G， THITE A N， THOMPSON D J. A threshold for the use of Tikhonov regularization in inverse force determination[J]. Applied Acoustics， 2006， 67（7）： 700-719.

[11]张磊，曹越云.总体最小二乘正则化算法的载荷识别[J].振动与冲击，2014， 33（9）：159-164.

ZHANG Lei， CAO Yueyun. Load identification using CG-TLS regulariztion algorithm[J]. Journal of Vibration and Shock， 2014， 33（9）： 159-164.（In Chinese）

[12]韩旭，刘杰.时域内多源动态载荷的一种计算反求技术[J].力学学报，2009， 41（4）：595-602.

HAN Xu， LIU Jie. A computational reverse technique for multi source dynamic loads in time domain[J]. ACTA Mechanica， 2009， 41（4）： 595-602.（In Chinese）

[13]常晓通，阎云聚.基于Green函数和正则化的动态载荷识别方法[J].振动、测试与诊断，2014， 34（1）：124-129.

CHANG Xiaotong， YAN Yunju. Dynamic load identification method based on Green function and regularization[J]. Journal of Vibration，Measurement & Diagnosis， 2014， 34（1）： 124-129.（In Chinese）

[14]郭榮，房怀庆.基于Tikhonov正则化及奇异值分解的载荷识别方法[J].振动与冲击，2014， 33（6）：53-58.

GUO Rong， FANG Huaiqing. Novel load identification method based on the combination of Tikhonov regularization and singular value decomposition[J]. Journal of Vibration and Shock， 2014， 33（6）： 53-58.（In Chinese）

[15]HAY N C， ROBERTS D E. Road simulators： the iterative algorithm for drive file creation[C]//2006 SAE World Congress.Detroit， Michigan， 2006： 2006-2011.

[16]陈栋华，靳晓雄，周鋐.汽车室内道路模拟试验系统控制算法的研究[J].噪声与振动控制，2006（1）：31-35.

CHEN Donghua， JIN Xiaoxiong， ZHOU Hong. Study on contorl algoirthm for vehicle road simulation test system[J]. Noise and Vibration Control， 2006（1）： 31-35.（In Chinese）

[17]杜永昌.车辆道路模拟试验迭代算法研究[J].农业机械学报，2002， 33（2）：5-7.

DU Yongchang. Research on iteration algorithm used for vehicle road simulation[J]. Transactions of the Chinese Society of Agricultural Machinery， 2002， 33（2）： 5-7.（In Chinese）

[18]汪斌，过学迅，李孟良.基于迭代学习控制的道路模拟算法[J].汽车工程，2010， 32（8）：686-689.

WANG Bin， GUO Xuexun， LI Mengliang. Road simulation algorithn based on iterative leaming control[J]. Automotive Engineering， 2010， 32（8）： 686-689.（In Chinese）

[19]O'CALLAHAN J C. A procedure for an improved reduced system （IRS） model[C]//Proceedings of the 7th International Modal Analysis.Las Vegas： Union College Press， 1989： 17-21.

[20]禇志刚，夏金凤，王光建.循环对称结构重根模态振型相关性修正[J].机械工程学报，2014， 50（23）：60-64.

CHU Zhigang， XIA Jinfeng， WANG Guangjian. Correlation correction for doublet mode shapes of cyclic symmetric structures[J]. Journal of Mechanical Engineering， 2014， 50（23）： 60-64.（In Chinese）