基于量本利分析法的房地产开发项目经济评价

朱朦++于凤光+沈聪

摘要： 量本利分析法通过研究分析项目产量、成本、利润三者之间的关系，得到项目方案的盈亏平衡点，从保本角度来反应项目投资风险。本文将量本利分析法与房地产项目开发相结合，将其运用于房地产开发项目前期决策阶段，为房地产开发项目的成本控制、项目风险预测、企业经营状态等提供参考，为决策提供科学合理的依据。

Abstract： Through the research and analysis of the relationship among project yield， cost and profit， the amount of principal and interest analysis gets the breakeven point of the project to reflect the risk of project investment from the perspective of capital protection. This paper combines quantity cost profit analysis with real estate development to use them in the prophase decision stage of the real estate development projects to provide references for the cost control， project risk prediction， enterprise management status of the real estate development projects and provide scientific and reasonable basis for decision-making.

关键词： 量本利分析；房地产；项目开发

Key words： principal and interest analysis；real estate；project development

中图分类号：F293.3 文献标识码：A 文章编号：1006-4311（2017）07-0029-04

0 引言

当今房地产行业竞争激烈，房地产开发企业必须对项目进行准确的前期决策及经济评价。量本利分析法在多个领域中广泛应用，但在房地产开发中应用较少。本文将量本利分析法并结合Excel拟合的非线性模型运用到房地产开发项目的前期决策阶段，分析得到开发项目保本开发量，最佳开发量，经营安全率，企业成本费用控制等，为房地产开发项目前期决策及经济评价提供科学合理的依据。

1 房地产开发相关概念

1.1 房地产的含义

房地产包括房产与地产，是指土地及其定着在土地之上的建筑物和其他附属物的总称[1]。进行房地产概念界定的原则：①房产和地产二者耦合不可分离。②一般情况下，房地产概念中的“地”是指承载用地。③一般情况下，房地产界定需从房屋建筑出发。④房地产的定义（内涵）具有层次性。

综合上述可将房地产定义为：房地产是指土地、建筑物和其他附属物所衍生出的各种财产权利。

1.2 房地产开发的基本概念

房地产开发的概念是房地产开发企业根据城市规划对国有建设用地进行房屋建设、基础设施的行为。

房地产开发首先要依据城市规划，坚持全面规划，合理布局，经济效益与社会效益兼顾。房地产开发具有综合性、长期性、时序性、地域性、风险性等特性。

2 量本利分析法的基本概念、原理及一般模型

2.1 量本利分析法的基本概念

“量”即为数量。在一般情況下，量为销售数量，为了方便研究和分析，我们有时把销售数量等于生产数量。

“本”即为成本。我们把总成本划分为固定成本和可变成本。一般情况下，在一定的生产规模内，固定成本是不随产品产量的变动而变动的成本，可变成本是随产品产量的变动而变动的成本[3]。

“利”即为利润。在生产经营活动中产生的盈利，在数值上利润=销售收入减-销售税金及附加-总成本 （总成本=固定成本+可变成本）。

2.2 量本利分析法的基本原理

量本利分析法是通过研究及分析数量、成本和利润之间的关系，找出项目方案在盈利与亏损临界点时产量、单价、成本的临界值，盈亏临界点即为保本点。反映了在一定的生产经营状态下项目方案的产量、利润与成本的平衡关系[4]。

2.3 量本利分析法的一般模型

2.3.1 线性量本利分析法模型

从图2中可以看出， 销售收入R与总成本C的交点，即为盈亏平衡点（Break Even Point，BEP），BEP对应的横坐标Q0即为盈亏平衡时的产量，其对应的纵坐标R0即为盈亏平衡时的销售收入。当产量QQ0时，R>C，即盈利。盈亏平衡点的Q0越小，企业保本点越低，盈利空间越大，生产经营风险越小。

2.3.2 非线性量本利分析法模型

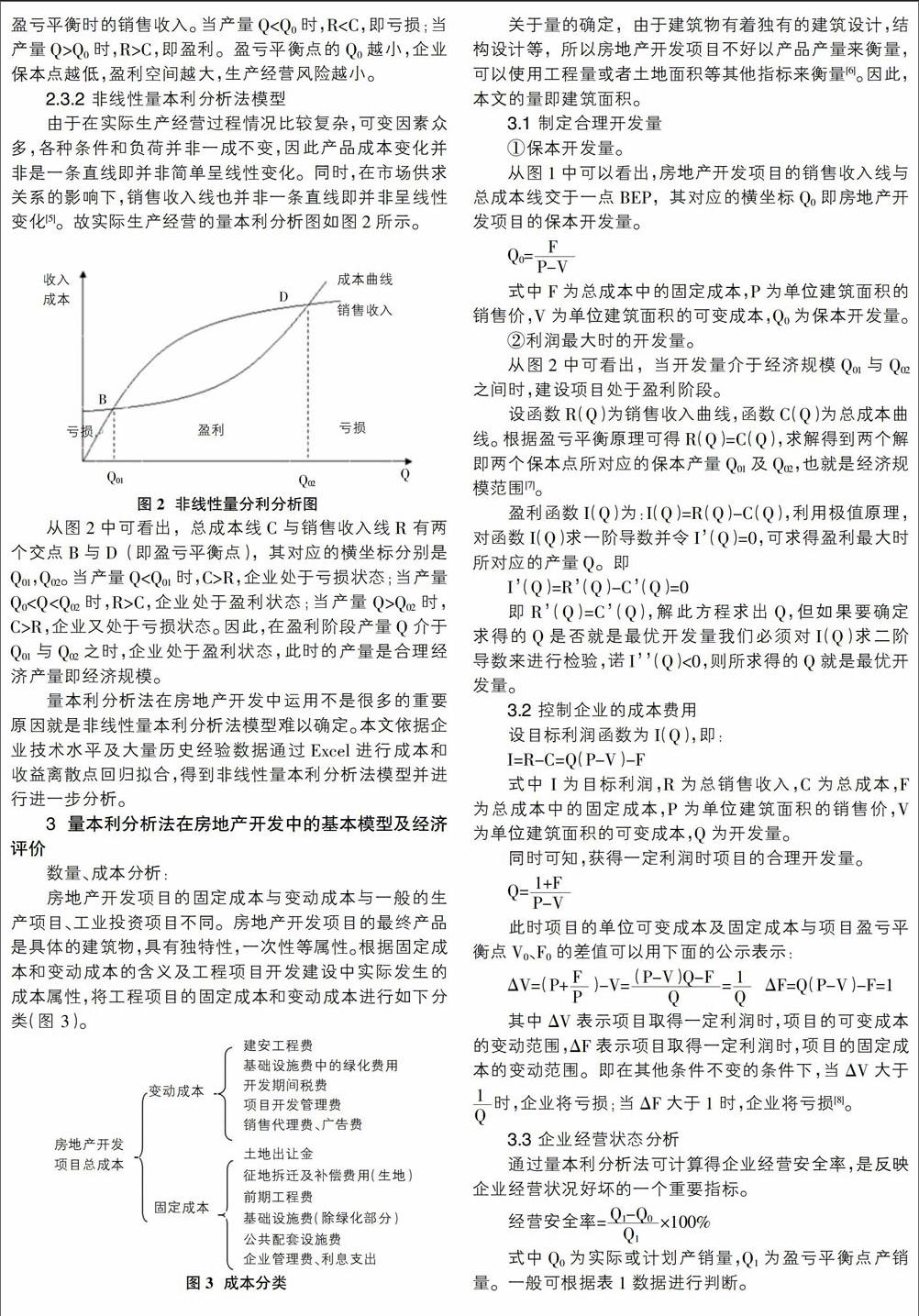
由于在实际生产经营过程情况比较复杂，可变因素众多，各种条件和负荷并非一成不变，因此产品成本变化并非是一条直线即并非简单呈线性变化。同时，在市场供求关系的影响下，销售收入线也并非一条直线即并非呈线性变化[5]。故实际生产经营的量本利分析图如图2所示。

从图2中可看出，总成本线C与销售收入线R有两个交点B与D（即盈亏平衡点），其对应的横坐标分别是Q01，Q02。当产量QR，企业处于亏损状态；当产量Q0C，企业处于盈利状态；当产量Q>Q02时，C>R，企业又处于亏损状态。因此，在盈利阶段产量Q介于Q01与Q02之时，企业处于盈利状态，此时的产量是合理经济产量即经济规模。

量本利分析法在房地产开发中运用不是很多的重要原因就是非线性量本利分析法模型难以确定。本文依据企业技术水平及大量历史经验数据通过Excel进行成本和收益离散点回归拟合，得到非线性量本利分析法模型并进行进一步分析。

3 量本利分析法在房地产开发中的基本模型及经济评价

数量、成本分析：

房地产开发项目的固定成本与变动成本与一般的生产项目、工业投资项目不同。房地产开发项目的最终产品是具体的建筑物，具有独特性，一次性等属性。根据固定成本和变动成本的含义及工程项目开发建设中实际发生的成本属性，将工程项目的固定成本和变动成本进行如下分类（图 3）。

关于量的确定，由于建筑物有着独有的建筑设计，结构设计等，所以房地产开发项目不好以产品产量来衡量，可以使用工程量或者土地面积等其他指标来衡量[6]。因此，本文的量即建筑面积。

3.1 制定合理开发量

①保本开发量。

从图1中可以看出，房地产开发项目的销售收入线与总成本线交于一点BEP，其对应的横坐标Q0即房地产开发项目的保本开发量。

式中F为总成本中的固定成本，P为单位建筑面积的销售价，V为单位建筑面积的可变成本，Q0为保本开发量。

②利润最大时的开发量。

从图2中可看出，当开发量介于经济规模Q01与Q02之间时，建设项目处于盈利阶段。

设函数R（Q）为销售收入曲线，函数C（Q）为总成本曲线。根据盈亏平衡原理可得R（Q）=C（Q），求解得到两个解即两个保本点所对应的保本产量Q01及Q02，也就是經济规模范围[7]。

盈利函数I（Q）为：I（Q）=R（Q）-C（Q），利用极值原理，对函数I（Q）求一阶导数并令I（Q）=0，可求得盈利最大时所对应的产量Q。即

I（Q）=R（Q）-C（Q）=0

即R（Q）=C（Q），解此方程求出Q，但如果要确定求得的Q是否就是最优开发量我们必须对I（Q）求二阶导数来进行检验，诺I（Q）<0，则所求得的Q就是最优开发量。

3.2 控制企业的成本费用

设目标利润函数为I（Q），即：

I=R-C=Q（P-V）-F

式中 I为目标利润，R为总销售收入，C为总成本，F为总成本中的固定成本，P为单位建筑面积的销售价，V为单位建筑面积的可变成本，Q为开发量。

3.3 企业经营状态分析

通过量本利分析法可计算得企业经营安全率，是反映企业经营状况好坏的一个重要指标。

式中Q0为实际或计划产销量，Q1为盈亏平衡点产销量。一般可根据表1数据进行判断。

通过安全经营率可反映房地产企业经营状况好坏，安全性高低等，使项目前期决策更加的科学、合理。

4 案例分析

本项目总建筑面积16363平方米，其中地上总建筑面积10523平方米，地下总建筑面积5840平方米。房地产开发项目总成本如表2。住宅每平米售价23000元/m2，共10523平方米；车库售价12000元/个，共124个；地下储藏室售价5000元/m2，共1191.06平方米。

4.1 保本开发量

由表2可知本项目固定成本为13976.86万元，总变动成本为7455.14万元，因为总建筑面积是16363平方米，可得单位可变成本为4556.10元/平方米。

再进行平均单价估算：

住宅收益即地上收益，23000 Q10523=237215790.00元，平均价格23000元/m2；

地下收益，12000Q124+5000Q1191.06=20835300.00元；平均价格3567.69元/m2；

总收益=237215790.00+20835300.00=25805.11万元

地上建筑比例=10523/16363=0.643097；

地下建筑比例=5840/16363=0.356903；

本项目计划开发量（Q1）为16363m2>12144.86m2，及Q1>Q0，所以本项目可行。

4.2 企业经营状态分析

由表1可知，26%∈[25%，30%]，即本项目的经营状态为较安全。

4.3 企业成本费用控制

本项目的目标利润I为4373.11万元，建筑面积Q为16363平方米。盈亏平衡点时固定成本为13976.86万元，单位可变成本为4556.10元/平方米。得：

也就是说在其他条件不变的情况下，项目的可变成本在盈亏平衡点V0即4556.10元/平方米的基础上涨幅不得超过2672.56元/平方米，否则企业将亏损；项目的固定成本在盈亏平衡点F0即13976.86万元的基础上，涨幅不得超过4373.11万元，否则企业将亏损。

4.4 最佳开发量

诺要求得最佳开发量，就要知道销售收入曲线的函数式R（Q）和总成本曲C（Q）。根据本企业自身的技术水平和大量经验数据估算出相应建筑面积下的开发成本和收益。本案例在根据本公司现有的开发技术水平和参考大量经验数据后，在前期估算出相应建筑面积下的开发成本和收益。通过Excel分别对大量的成本和收益离散点进行回归拟合，得到销售收入函数R（Q）和总成本函数C（Q）。如图4 成本、收益、利润回归曲线图所示。虽然该图并没有从（0，0）点开始计算，但是我们所要求的是非线性量本利分析在两个保本点之间求最大盈利值，因此所选取的建筑面积范围（包含两个保本点）已满足计算要求。虽然个别点偏离回归曲线，但是整体回归函数不受个别点影响，所得回归函数正确可用。

由图4可得，通过计算机拟合的回归函数分别为：

成本C（Q）=0.0007Q2-21.251Q+190912

销售收入R（Q）=-0.0002Q2+9.5887Q-68471.08

则利润函数为：

I（Q）=R（Q）-C（Q）=-0.0002Q2+9.5887Q-68471.08-0.0007Q2+21.251Q-190912=-0.0009Q2+30.839Q-259383.1

即利润函数I（Q）=-0.0009Q2+30.839Q-259383.1

利用极值原理得I（Q）=-0.0018Q+30.839，并令其等于0，得Qm=17132.78。

但诺要检验所求得的Q是否就是最大盈利时的最优开发量，还必须通过对I（Q）求二阶导数并进行檢查。

I（Q）=-0.0018<0，由极值定理得Qm是I（Q）在所选取你范围内的最大值。即本项目根据非线性量本利分析法所求的最佳开发建筑面积为17132.78平方米，此时利润最大为I（Qm）=4795.79万元。目前本项目的开发建筑面积是16363平方米，总销售收入是25805.11，所得总利润是销售收入减去总成本，为4373.11万元。即在最佳开发量时比现在净利润增加4795.79-4373.11=422.68万元。

5 结语

房地产市场竞争日益激烈，房地产开发企业必须对项目进行准确的经济评价及前期决策，必须对项目的运作采取相应的措施进行有效的管控。这是当今房地产开发企业取得项目成功开发的关键。

在房地产开发项目的前期决策阶段，应用量本利分析法，依据市场行情及企业以往项目开发历史数据进行项目经济评价，得到开发项目保本开发量，最佳开发量，企业经营安全率，企业成本费用控制等，提高房地产开发项目前期决策水平。

参考文献：

[1]周小平，熊志刚.房地产开发与经营[M].北京：清华大学出版社，2010.

[2]王新芳.房地产开发成本控制研究[D].西安：西安科技大学， 2008.

[3]许婷华，曲成平，杨淑娟.建设工程经济[M].武汉大学出版社，2014.

[4]黄有亮.工程经济学（第二版）[M].南京：东南大学出版社，2006.

[5]毛义华.工程经济学[M].浙江大学出版社，2014.

[6]孟君娜.建设工程经济[M].武汉理工大学出版社，2014.

[7]宋宁.探讨量本利分析法在利润成本决策中的应用[J].中国外资，2013（11）：15-16.

[8]汪景仁.量本利分析法在施工管理中的应用[J].水科学与工程技术，2005（05）：5-7.

[9]赵青.试论量、本、利分析法在工程管理中的应用[J].中国建设信息，2001（31）：43-46.