基于FLUENT的滴灌条件下土壤水分入渗数值模拟
祁毓婷,郑德聪,王璟,薛楠,高洁
(山西农业大学 工学院,山西 太谷 030801)
基于FLUENT的滴灌条件下土壤水分入渗数值模拟
祁毓婷,郑德聪*,王璟,薛楠,高洁
(山西农业大学 工学院,山西 太谷 030801)
[目的]研究滴灌过程中土壤水分的入渗规律对合理滴灌与作物增产有重要意义。[方法]本文采用Fluent软件对行距为50 cm的滴灌种植模式计算求解。[结果]通过模拟得到土壤水分入渗的速度分布云图与各点水分分布云图。模拟结果与实际试验结果基本一致,入渗速度随入渗深度和宽度的增加而减小,水平方向和垂直方向的平均入渗速度分别为2.73×10-4m·s-1、2.24×10-4m·s-1,水平方向入渗速度较大;水分到达距地面10 cm深处作物根部所需时间大约为100~120 min;入渗时各点土壤含水率增速随时间下降,随宽度和深度的增加而减小。[结论]模拟结果表明,数值模拟能够较好地反映滴灌条件下土壤水分入渗规律,为确定最优种植模式提供理论指导。
Fluent;滴灌;土壤;水分入渗;数值模拟
滴灌作为一种新型节水灌溉技术已广泛应用于各种作物灌溉当中。合理的滴灌模式能够提高作物产量,同时也能节省灌溉用水[1]。研究滴灌过程中水分在土壤中的入渗规律对优化滴灌模式有重要意义。 王成武等[2]采用人工配置试验土壤的方法,研究了不同滴灌条件下水分在土壤中的分布形式。冀荣华等[3]和李耀刚等[4]分别使用HYDRUS-2D和HYDRUS-3D软件对负压灌溉和涌泉根灌进行数值模拟,得到了不同灌水半径和不同灌水定额下土壤水分入渗规律。但对于在一定行距和灌水定额下土壤水分入渗速度、水分到达作物根部所需时间以及水分入渗后各点土壤含水率的分布规律还鲜见报道。
本文采用Fluent软件对行距50 cm、灌水定额每箱4 L条件下土壤水分入渗过程进行数值模拟和试验,通过模拟得到土壤水分入渗的速度分布云图以及入渗各点水分分布云图,分析云图中各点的土壤含水率,对照试验所得数据,研究滴灌后水分随时间的入渗规律。
1 基本理论和方法
1.1 模拟基本理论
土壤是一种多孔介质,由无数形状不规则且排列错综复杂的固体颗粒组成,水分在土壤中的运动是复杂且多变的[5],因此在模拟过程中采用多孔介质模型。模拟原理为动量守恒原理,对于不可压缩流体,要在模拟过程中启用能量方程[6]。由于入渗过程是水在土壤孔隙中的流动,土壤介质孔隙大小不一,分布错综复杂,故对流体产生较大阻力,Fluent在对其模拟时应在原有动量方程的基础上增加一个动量源项,该项由粘性损失项和内部损失项组成[7],能够真实反映土壤介质对水分流动的实际阻力。
1.2 模型建立
滴灌属于点源入渗[8],假定土壤为均质土壤,在各向同性的条件下可以将三维入渗模型简化为二维入渗模型[9]。由于本试验在室内进行,故不考虑水分蒸发和降水对土壤水分入渗的影响。采用ICEM软件建立数学模型,模型最大水平宽度为作物种植行距50 cm,最大垂直距离根据田间试验所测数据选取40 cm。滴灌带置于土壤水平面中心处,滴孔水源入渗宽度为4 cm。所建模型为二维模型,故将速度入口直径简化为入口宽度D。建立模型如图1所示。

图1 土壤水分入渗示意图Fig.1 Diagram of water infiltration
图1中O为坐标原点,O'为滴灌带中心,ABCD为数值模拟区域,ab为水源入渗宽度。数值模拟区域水平距离X/cm为闭区间[-25,25],垂直距离OO'=40 cm,ab=4 cm。
1.3 边界条件设置
分别设置进口速度(velocity-inlet)、出口压力(pressure-outlet)和温度(temperature)等边界条件。由于滴灌过程较缓慢,且滴孔较小,所以采用试验测量的方法来确定模型的进口速度。在水头压力为0.04 MPa的条件下,分别选取3处滴孔测量其60 s内的滴灌量Q/m3,根据滴灌量Q/m3,以及水源入渗宽度D/m由公式(1)计算其进口速度v,每处滴孔测量3次,共测9次。测量结果如表1所示。
v=4Q/πD2t
(1)

表1 各点滴灌速度测量值
由表1中各点进口速度取其平均值可得,进口速度v=4.23×10-4m·s-1。
出口压力为标准大气压P=1.01×105Pa,温度为室内温度T=298 K。
1.4 数值模拟
本次模拟的区域条件为多孔介质(porous),均匀划分模型区域网格。多孔介质模型粘性阻力系数和惯性阻力系数由土壤特性确定其值,土壤孔隙率[10]为0.4。模拟采用时间步长为0.01 s,共模拟120 min。
2 滴灌土壤入渗试验
2.1 试验材料与装置
选取山西省太谷县侯城乡杨家庄试验区石灰型褐土为试验土壤,其质地为中壤土,配比为有机质含量约18.7 g·kg-1,全氮含量约1.56 g·kg-1,速钾含量约0.15 g·kg-1。
试验装置主要包括:滴灌带灌水系统,由滴灌带、水泵、控制测量仪表、干管、精密压力表、闸阀、流量调节器和滴头组成;DHG-9023A型电热恒温鼓风干燥箱;土钻;铝盒;电子天平,量程500 g,精度0.01 g;塑料土箱,80 cm×60 cm×40 cm(长×宽×高),土箱内放置土壤深度为40 cm。
2.2 试验方案
本试验于室内进行,试验前将所取土壤风干,使其初始含水率保持在5.1%~5.3%之间[11]。在塑料土箱中装土,滴灌带置于土壤上表面,位于土箱中央,调节滴灌带灌水系统,设置试验初始参数,水头压力为0.04 MPa,滴灌带流量大约为2 L·h-1。开始滴灌后,分别在距滴灌带滴孔水平方向双侧5、10、15、20、25 cm处取点,其俯视图如图2所示。每隔30 min用土钻在各点取土,每点取土深度为20 cm。分别取出土钻中深度为5、10、15、20 cm处的相同质量土壤,通过公式(2)计算土壤含水率并记录数据。试验通过测量滴灌后不同时间各点土壤含水率大小,确定土壤水分的运移情况。
(2)
式中:θ为土壤含水率/%;ω1为湿土与铝盒重量/g;ω2为干土与铝盒重量/g;ω为铝盒重量/g。

图2 试验测试点分布俯视图Fig.2 Distribution of testing points in top view 注:1.塑料土箱 2.取土样点 3.滴灌带 4.滴孔Note:1.Soil box of plastic 2.The point of sample soil 3.Drip tape 4.The hole of drip tape
3 结果与分析讨论
3.1 模拟结果分析
图3为100 min时水分入渗速度分布云图,表示滴灌100 min时各点的水分入渗速度。由图3可见,在距滴孔相同距离的水平方向与垂直方向上,距滴孔越远,入渗速度越小;比较其速度大小,并根据不同速度所占比例计算速度平均值,得到水平方向的平均入渗速度vx=2.73×10-4m·s-1,垂直方向的平均入渗速度vy=2.24×10-4m·s-1,水平方向的入渗速度总体大于垂直方向。滴灌初期,土壤初始含水率较低,土壤入渗能力大,入渗较快。随着水分的不断入渗,土壤含水率增大,其渗透力减小,入渗变慢。

图3 入渗速度分布云图Fig.3 The counter of infiltration velocity
图4(a)~(d)分别为开始滴灌30、60、90、120 min后土壤水分入渗的水分分布云图。由图4可见,水分入渗范围随时间逐渐变大,30 min时水分到达水平方向约8 cm处,入渗深度约5 cm;60 min时水分到达水平方向约15 cm处,入渗深度约10 cm;90 min时水分到达水平方向约20 cm处,入渗深度约15 cm;120 min时水分到达水平方向约25 cm处,入渗深度约20 cm。由此可估计,在行距为50 cm的种植模式下,作物位于距滴灌带滴孔水平距离25 cm处,经过100~120 min水分可到达作物根部。
在滴灌过程中,入渗各点的土壤含水率随时间不断增大[12],根据图中土壤含水率的变化梯度可得,水平方向的土壤含水率增速大于垂直方向。随着种植深度和宽度的增加,土壤含水率增速减小。由此可得,种植行距越大,水分到达作物根部所需时间越长。
3.2 实测结果分析
图5为不同深度各点土壤含水率随时间变化的曲线图,其中的5条曲线分别代表距滴灌带滴孔水平距离5、10、15、20、25 cm处的土壤含水率变化。由图5可见,随着滴灌进行,土壤各处的含水率均明显增大,但增速没有明显规律;滴灌100~120 min后,水分能到达距滴灌带滴孔水平方向

图4 不同时间水分入渗分布云图Fig.4 Contours of water infiltration in different time(a)t=30 min;(b)t=60 min;(c)t=90 min;(d)t=120 min
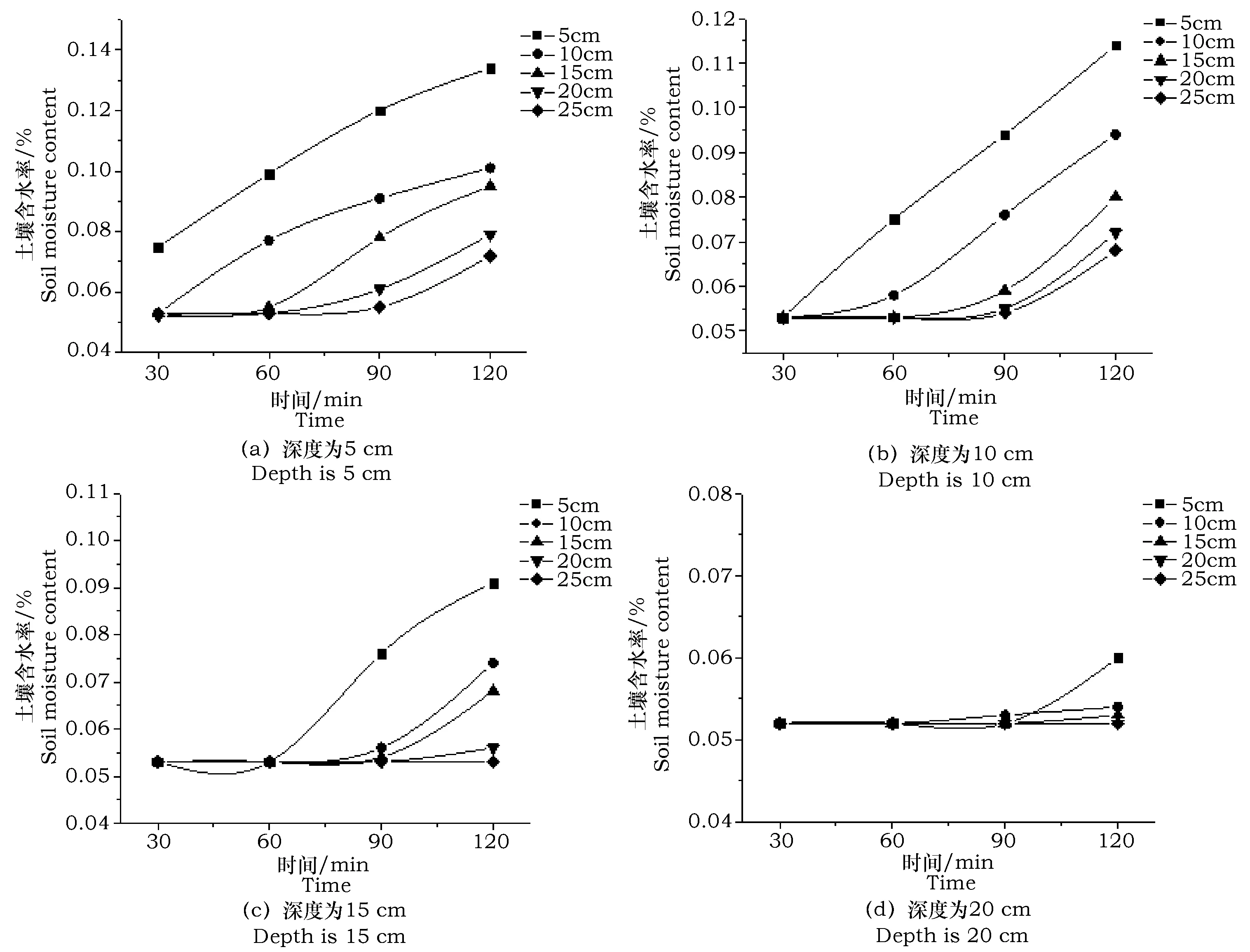
图5 不同深度各点土壤含水率随时间变化曲线Fig.5 Soil moisture content variation with time in different depth
25 cm、深度为10 cm处,因此在行距为50 cm、种植深度为10 cm的种植模式下,滴灌100~120 min后水分能到达作物根部。
3.3 结果有效性验证
由模拟结果与实测结果的分析比较可知,模拟值与实测值较为接近。其结论基本一致,因此模拟结果能够较好的反映实际入渗过程。造成误差的原因与土壤初始含水率及试验过程中取土准确性等因素有关。且本次试验为室内试验,未种植作物,所以模拟过程中不考虑水分蒸发、降雨以及作物根部对水分的吸收等因素影响,在今后的研究中需进一步讨论。
4 结论
(1)各点土壤水分入渗模拟值和实际试验值基
本一致,所建模型能够较好地模拟滴灌条件下土壤水分入渗规律,可以用于研究滴灌条件下的土壤水分入渗规律。
(2)滴灌时水分在水平方向的入渗速度总体大于垂直方向的入渗速度,水平方向和垂直方向的平均入渗速度分别为vx=2.73×10-4m·s-1和vy=2.24×10-4m·s-1。
(3)滴灌100~120 min后,水分能够初步到达水平方向25 cm、垂直方向10 cm处。行距为50 cm的种植模式下水分到达作物根部10 cm处所需时间大约为100~120 min。
[1]王成武,戈振扬.滴灌条件下土壤渗流分形特性研究[J].昆明理工大学学报,2007,32(1):105-107.
[2]张志刚,李宏,李疆,等.地表滴灌条件下滴灌量对土壤水分入渗再分布过程的影响[J].农业现代化研究,2016,37(1):174-181.
[3]冀荣华,王婷婷,祁力钧,等.基于HYDRUS-2D的负压灌溉水分入渗数值模拟[J].农业机械学报,2015,46(4):113-119.
[4]李耀刚,王文娥,胡笑涛.基于HYDRUS-3D的涌泉根灌土壤入渗数值模拟[J].排灌机械工程学报,2015,31(6):546-552.
[5]黄昌勇.土壤学[M].北京:中国农业出版社,2005:78-79.
[6]韩占中.FLUENT—流体工程仿真计算实例与分析[M].北京:北京理工大学出版社,2009:84-85.
[7]唐家鹏.FLUENT14.0超级学习手册[M].北京:人民邮电出版社,2013:434-435.
[8]郑园萍.滴灌条件下土壤水分入渗过程模拟试验研究[D].杨凌:西北农林科技大学,2008.
[9]雷志栋,杨诗秀.非饱和土壤水一维流动的数值计算[J].土壤学报,1982,19(2):141-152.
[10]李晓斌,孙海燕.不同土壤质地的滴灌点源入渗规律研究[J].科学技术与工程,2008,8(15):4292-4295.
[11]赵西宁,吴发启.土壤水分入渗的研究进展和评述[J].西北林学院学报,2004,19(1):42-45.
[12]Zhang Zhenhua, Cai Huanjie,Guo Yongchang, et al. Experimental study on factors effecting soil wetted volume of clay loam under drip irrigation[J].Transactios of the CSAE,2002,18(2):17-20.
(编辑:李晓斌)
Numerical simulation of drip irrigation soil water infiltration laws on Fluent
Qi Yuting, Zheng Decong*, Wang Jing, Xue Nan, Gao Jie
(CollegeofEngineering,ShanxiAgriculturalUniversity,TaiguShanxi030801,China)
[Objective]Research in the process of the drip irrigation infiltration laws of soil water infiltration has important significance for reasonable drip irrigation and crop yield increase.[Methods]This text used Fluent software to simulate the drip irrigation planting patterns of 50 cm space to calculate the soil water infiltration.[Results]It got the contours of velocity distribution and moisture distribution. Simulation results and actual test results were in agreement.Infiltration velocity decreased with the increase of infiltration depth and width. The average infiltration rate of horizontal direction and vertical direction were 2.73×10-4m·s-1and 2.24×10-4m·s-1, horizontal infiltration rate was greater than the vertical infiltration rate; it needed about 100~120 min for water to arrive the depth of 10cm at crop roots; the soil moisture content in each point decreased over time, and with the increase of width and depth, the soil moisture content decreased. [Conclusion]The results showed that the numerical simulation can reflect the rule of soil water infiltration under drip irrigation. It provided theoretical guidance for determining the optimal planting pattern.
Fluent, Drip irrigation, Soil, Infiltration, Numerical simulation
2016-06-20
2016-10-18
祁毓婷(1992-),女(汉),山西忻州人,硕士研究生,研究方向:节水灌溉理论与技术
*通信作者:郑德聪,教授,硕士生导师。Tel:0354-6288906;E-mail:Zhengdecong@126.com
S275.6
A
1671-8151(2017)02-0141-05

