广义时滞系统稳定和镇定的严格线性矩阵不等式判据
张雪峰, 潘红燕, 薛定宇(东北大学 . 理学院; . 信息科学与工程学院, 辽宁 沈阳 110004)
广义时滞系统稳定和镇定的严格线性矩阵不等式判据
张雪峰a, 潘红燕a, 薛定宇b
(东北大学 a. 理学院; b. 信息科学与工程学院, 辽宁 沈阳 110004)
用构造P矩阵和Lyapunov直接稳定性方法,用简便的严格线性矩阵不等式(LMIs)给出了线性广义时滞系统的稳定和镇定判定条件. 得到了广义时滞系统的容许性严格LMI充分条件; 给出了两类状态反馈控制器来保证闭环系统的稳定性,因为所得LMIs判据中只需解出一个未知正定矩阵Q,故该LMIs判据简化和改进了已有结果;给出了仿真实例来验证所得判据的有效性.
广义时滞系统; 稳定性; 镇定性; 严格线性矩阵不等式
线性广义时滞系统也叫描述时滞系统、隐式时滞系统或者时滞微分代数系统,在过去的几十年里一直备受关注.并且它在工程系统中应用广泛,比如:化工过程、气动系统中的长距离输电线等.动态系统中时滞的出现将导致系统性能不佳[1-2],而且广义时滞系统的镇定和稳定性比正常系统的要复杂得多.然而经过大量学者们长期不懈的努力,广义时滞系统的研究取得了一系列进展.
早年文献[3]研究了广义系统,被大多数人所认可.文献[4]讨论了有状态时滞和参数不确定性的广义系统的鲁棒稳定性和镇定性问题.文献[5]用有等式约束的LMIs给出了状态时滞广义系统的稳定性和镇定性条件. 文献[6]研究了带有范数有界不确定性的广义时滞系统的时滞依赖稳定性判据.
近三年来广义时滞系统也一直是个热门话题.在文献[7]中,作者用严格LMIs给出了广义系统的容许性充要条件.文献[8]用线性Lyapunov泛函和正系统证明了时变时滞系统的稳定性.文献[9] 研究了离散广义时滞系统的一个新的容许性判据.在文献[10]中,作者用中立系统方法,通过LMIs 研究了一类变时滞线性广义系统的容许性问题. 而文献[11]用简便的LMIs解决了线性和离散广义系统的容许性问题.有趣的是,文献[12]研究了一类广义时滞不确定的网络化串级控制系统的镇定性和H∞控制问题.文献[13]研究了有状态饱和的广义时滞系统的时滞依赖H∞鲁棒指数稳定和记忆状态镇定问题.
尽管对于广义时滞系统稳定性的研究已有很多结果,但很少是简便和有效的. 其中文献[5]给出了广义时滞系统的稳定和镇定性的LMIs判据,但是这些LMIs不是严格的,而且包含两个未知矩阵P和Q. 正如我们所看到的,大部分已知LMIs判据都有等式约束,而它会导致计算机摄入误差.因此,亟需找到一个在数值计算上易处理的和可靠的广义时滞系统稳定性的LMI判据.本文受文献[14]的启发,用依赖于矩阵E的任意可逆矩阵M和N构造P,使未知矩阵减少为一个Q, 并使得LMIs是严格的.用此方法,我们给出了严格的和程序参数自由的LMI容许性判据,然后又用严格LMIs给出了闭环系统的两类不同的状态反馈控制器,由仿真实例可知文章中得到的LMIs都是简便可行的.
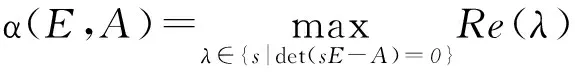
1 广义时滞系统的严格LMI稳定性判据
考虑如下线性广义时滞系统:
其中,x(t)∈Rn是系统状态变量,u(t)∈Rl是控制输入,E∈Rn×n是奇异矩阵,假设rank(E)=m
当τ=0时,广义时滞系统(1)退化为一般广义系统:
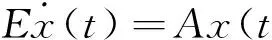
(2)
记为(E,A).
方便研究起见,下面首先给出广义时滞系统的容许的定义.
定义1[5]① 广义时滞系统(1)是正则和无脉冲的,如果对应系统(2)是正则,无脉冲的.
② 广义时滞系统(1)是稳定的,若对任意ε>0,都存在δ(ε)>0使得φ(t)满足sup‖φ(t)‖<δ(ε),其中-τ ③ 广义时滞系统(1)是容许的,若它是正则,无脉冲和稳定的. 为了得到想要的判据,知识准备如下: 引理1[3]设(E,A)是正则的,并且存在两个可逆矩阵M1和N1使得两式M1EN1=diag(I,J)和M1EN1=diag(A0,I)成立,则有 ① (E,A)是无脉冲的当且仅当J=0; ② (E,A)是稳定的当且仅当α(A0)<0; ③ (E,A) 是容许的当且仅当J=0,α(A0)<0, 引理3[5]考虑函数φ:R+→R,若φ在是一致连续且 则 φ(t)→0,t→∞. 当且仅当 引理5[5]广义系统(2) 是容许的当且仅当存在矩阵P使得 引理6[14]广义系统(2) 是容许的,若对于可逆矩阵M和N满足条件 使得 PTA+ATP<0. 其中,rank(E)=m,P=MTN-1. 下面给出广义时滞系统的严格LMI稳定性判据. 定理1 连续广义时滞系统(1)是容许的,如存在可逆矩阵M和N满足 和矩阵Q>0, 其中rank(E)=m,使得 证明 定理条件成立的前提下,运用引理4到式(3)可得 (4) 然后式(4)前后分别乘以N-T和N-1,并且令P=MTN-1得 易得 因此,由引理6可知(E,A)是容许的, 则根据定义1得广义时滞系统(1)是正则和无脉冲的.以下将证明广义时滞系统的稳定性: 其中,ηt=η(t+β),β∈(-τ,0]. 那么,可得函数V(ηt)沿着系统(1)轨迹对时间的微分如下: 若N1≠0,令 显然有 因此有 结合引理2和引理3得: ‖η1(t)‖=0,t→∞, 所以用证明上式的方法可证得: ‖η2(t)‖=0,t→∞. 当N1=0时,由类似方法也可得到结论 ‖η1(t)‖=‖η2(t)‖=0,t→∞. 故由定义1可知,广义时滞系统(1)是稳定的.综上所述,结合不等式(6)和定义1,显然可得系统(1)是容许的.定理得证. 推论1 连续广义时滞系统(1)是容许的,如果存在可逆矩阵M和N满足 和矩阵Q>0, 其中rank(E)=m,使得 证明 假设推论条件满足,结合引理4,用M-1和M-T分别左,右乘以式(12),且设P=NM-T可得: 用定理1的证明方法,结合引理5结论易得.证明完成. 对于广义时滞系统来说,找到一个控制器来保证它的稳定性,正则性和无脉冲性是很重要的. 考虑系统(1)及下面两种不同的状态反馈控制器: 运用控制器(14)到系统(1),可得闭环系统如下: 考虑闭环广义时滞系统(16),结合定理1和推论1,即可得想要结论. 定理2 对于系统(1)存在一个状态反馈控制器(14)使得闭环系统(16)是容许的,若存在适维矩阵Z1使得: 其中,Ξ1=NTATMT+MAN+MQMT+ u1(t)=Z1N-1x(t). (18) 下面运用控制器(15)到系统(1)可得闭环系统: 显然,对于闭环系统(19)有以下结论成立. 定理3 对于系统(1),存在状态反馈控制器(15)使得闭环系统(19)是容许的,如果存在适维矩阵Z2,Y和Q>0使得下面的不等式成立: 证明 结合引理4,把式(21)代入式(20),并用M-1和M-T分别左右乘之,最后记P=NM-T,则式(20)化为 因此由定理1和推论1,结论可证. 下面给出三个仿真实例,来验证所得结论的有效性. 例1 考虑系统(1),其参数如下: 其中矩阵M和N是通过文献[14]中的简单MATLAB命令,由LMI工具箱求得的,命令如下: n=3;OP=rref{[E,eye(n)]}; M=op(:,n+1:2*n);y=op(:,1:n)′; z=rref{[y,eye(n)]};N=z(;,n+1:2*n)′. 另一方面,由多项式det(sE-A)=(s+2)×(s+3)的解不全为零可知系统(1)是正则的;并且deg(det(sE-A))=rank(E)=2,也就是说系统(1)是无脉冲的;又因为多项式det(sE-A)=(s+2)(s+3)=0的根是-2和-3,显然实部都是负的,故系统(1)是稳定的;综上可得,系统(1)是容许的. 例2 考虑有如下参数的系统(1): 用MATLAB的LMI工具箱中的′feasp′命令解定理2中的式(17),所得可行解如下: 图1 例2中的闭环广义时滞系统状态图Fig.1 Statechart of closed-loop generalized time-delay system in example 2 由图1容易看出,反馈控制器(18)能使闭环广义时滞系统的状态镇定,因此所得状态反馈控制器是有效的. 由增益矩阵K2和L可得闭环广义时滞系统的状态曲线如图2.很容易看出,大约10 s内闭环广义时滞系统就可以被控制器(21)所镇定. 图2 例3中的闭环广义时滞系统状态图Fig.2 Statechart of closed-loop generalized time-delay system in example 3 本文研究了连续广义时滞系统的稳定和镇定问题,用构造矩阵变量和Lyapunov函数的方法,以严格线性矩阵不等式的形式给出了包含该系统稳定性的容许性判据,并设计出两类有效的状态反馈控制器以镇定不稳定系统,从图2中的状态曲线可以看出所设计控制器是有效的,并且由于所得LMIs中矩阵变量较少,因此用MATLAB中LMI工具箱解起来简便可行,便于应用. [1] SHAO Y Y,LIU X D,SUN X. A delay decomposition approach toH∞admissibility for discrete-time singular delay systems[J]. Information Sciences, 2014,279:893-905. [2] WU Z G,PARK J H,SU H Y. Delay-dependent passivity for singular Markov jump systems with time-delays[J]. Communications in Nonlinear Science and Numerical Simulation, 2013,18(3):669-681. [3] DAI L. Singular control systems[M]. New York: Springer-Verlag, 1989. [4] XU S Y,DOOREN P V,STEFAN R,et al. Robust stability and stabilization for singular systems with state delay and parameter uncertainty[J]. IEEE Transactions on Automatic Control, 2002,47(7):1122-1128. [5] XU S Y,LAM J. Robust control and filtering of singular systems[M]. Berlin: Springer-Verlag, 2006. [6] GAO H L,BU-GONG X U,ZHANG Y G. Delay-dependent robust stability criteria for two classes of uncertain singular time-delay systems[J]. IEEE Transactions on Automatic Control, 2007,52(5):880-885. [7] CHADLI M. Darouach M. Further enhancement on robust, control design for discrete-time singular systems[J]. IEEE Transactions on Automatic Control, 2014,59(59):494-499. [8] MAZENC F,MALISOFF M. Stability analysis for time-varying systems with delay using linear Lyapunov functionals and a positive systems approach[J]. IEEE Transactions on Automatic Control, 2016,61(3):771-776. [9] FENG Z,LI W,LAM J. New admissibility analysis for discrete singular systems with time-varying delay[J]. Applied Mathematics & Computation, 2015,265(C):1058-1066. [10] LIU Z Y,LIN C,CHEN B. Admissibility analysis for linear singular systems with time-varying delays via neutral system approach[J]. ISA Transactions, 2016,61:141-146. [11] ZHANG X F,CHEN Y Q. Improvement of strict LMI admissibility criteria of singular system: continuous and discrete[C]∥2015 ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Boston, Massachusetts, USA, August 2-5, 2015:1-4. [12] DU Z P,YUE D,HU S L.H∞stabilization for singular networked cascade control systems with state delay and disturbance[J]. IEEE Transactions on Automatic Control, 2014,10(2):882-894. [13] MA Y C,FU L.H∞robust exponential stability and memory state feedback control for uncertain singular time-delay systems with saturating actuators[J]. IET Control Theory & Applications, 2016,10(3):328-338. [14] ZHANG X F. Stability and stabilization of singular systems: strict LMI sufficient conditions[C]∥Proceedings of the 10th World Congress on Intelligent Control and Automation, 2012:1052-1055. 【责任编辑: 肖景魁】 Strict LMIs Conditions for Stability and Stabilization of Singular Delay Systems ZhangXuefenga,PanHongyana,XueDingyub (a. College of Science, b. College of Information Science and Engineering, Northeastern University, Shenyang 110004, China) The stability and stabilization criteria of continuous singular delay systems are presented by strict linear matrix inequalities(LMIs). Strict LMIs admissibility criteria are presented including stability of singular delay systems. Two class of state feedback controllers are given to guarantee that the given singular delay system is admissible. In the considered LMIs criteria, only a positive definite matrixQneeded to be solved without involving additional matrices. For this reason, the merit of obtained LMIs criteria is that they simplify and improve the existing results. Numerical examples are given to verify the effectiveness of the criteria. singular delay systems; stability; stabilization; strict LMIs 2016-09-02 国家自然科学基金资助项目(61673094). 张雪峰(1966-),男,辽宁辽阳人,东北大学副教授,博士; 薛定宇(1963-),男,辽宁沈阳人,东北大学教授,博士生导师. 2095-5456(2017)01-0082-05 TP 13 A
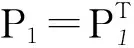
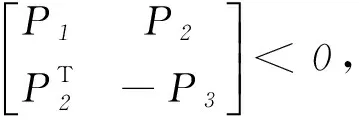
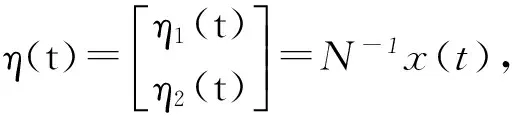
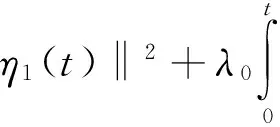
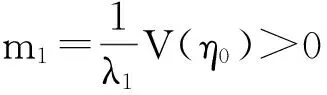
2 广义时滞系统的严格LMI镇定性判据
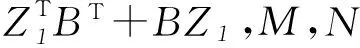
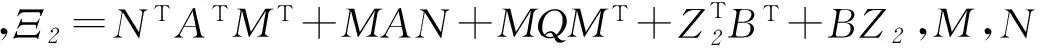
3 仿真实例
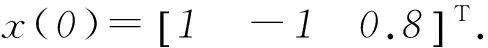
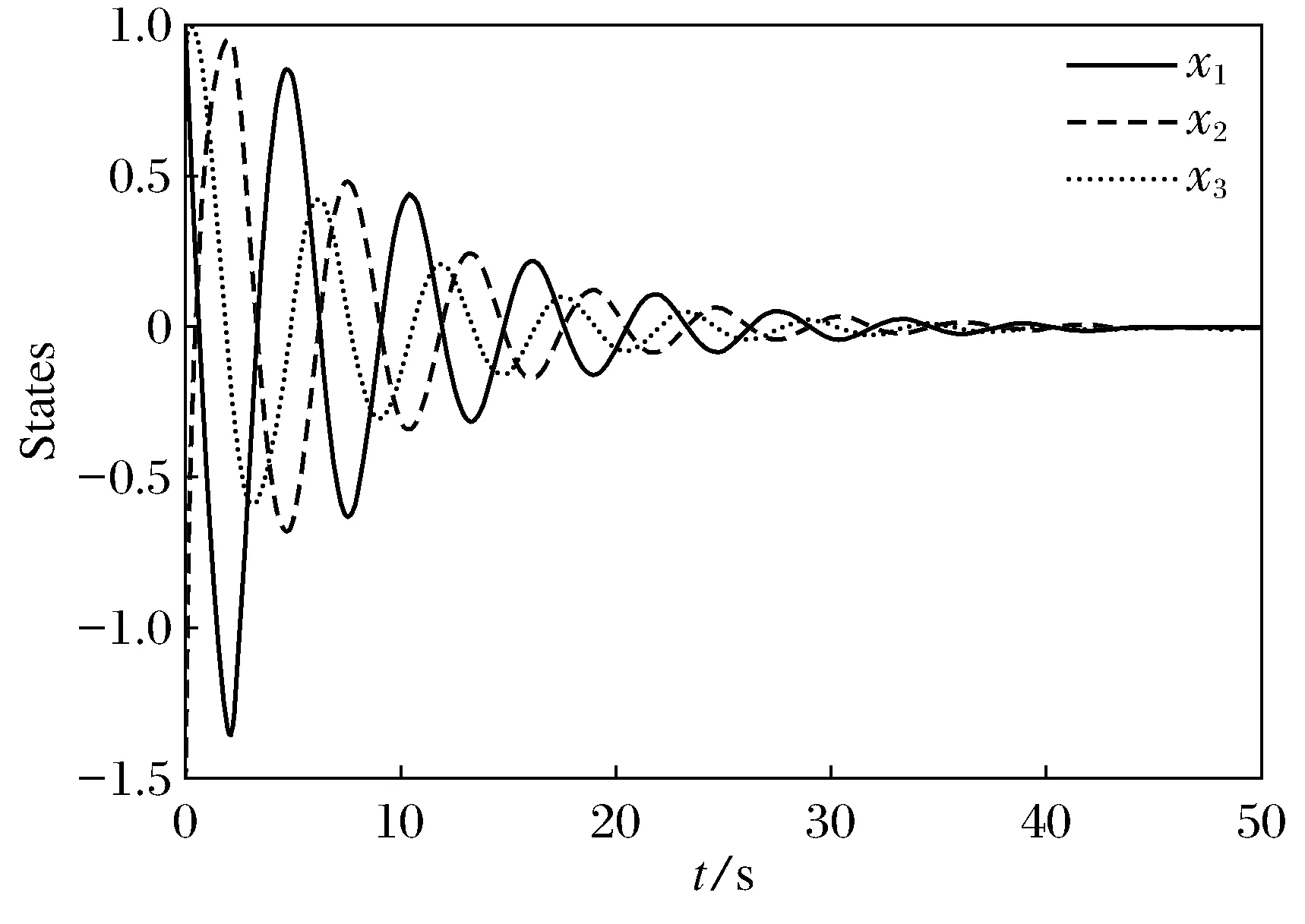
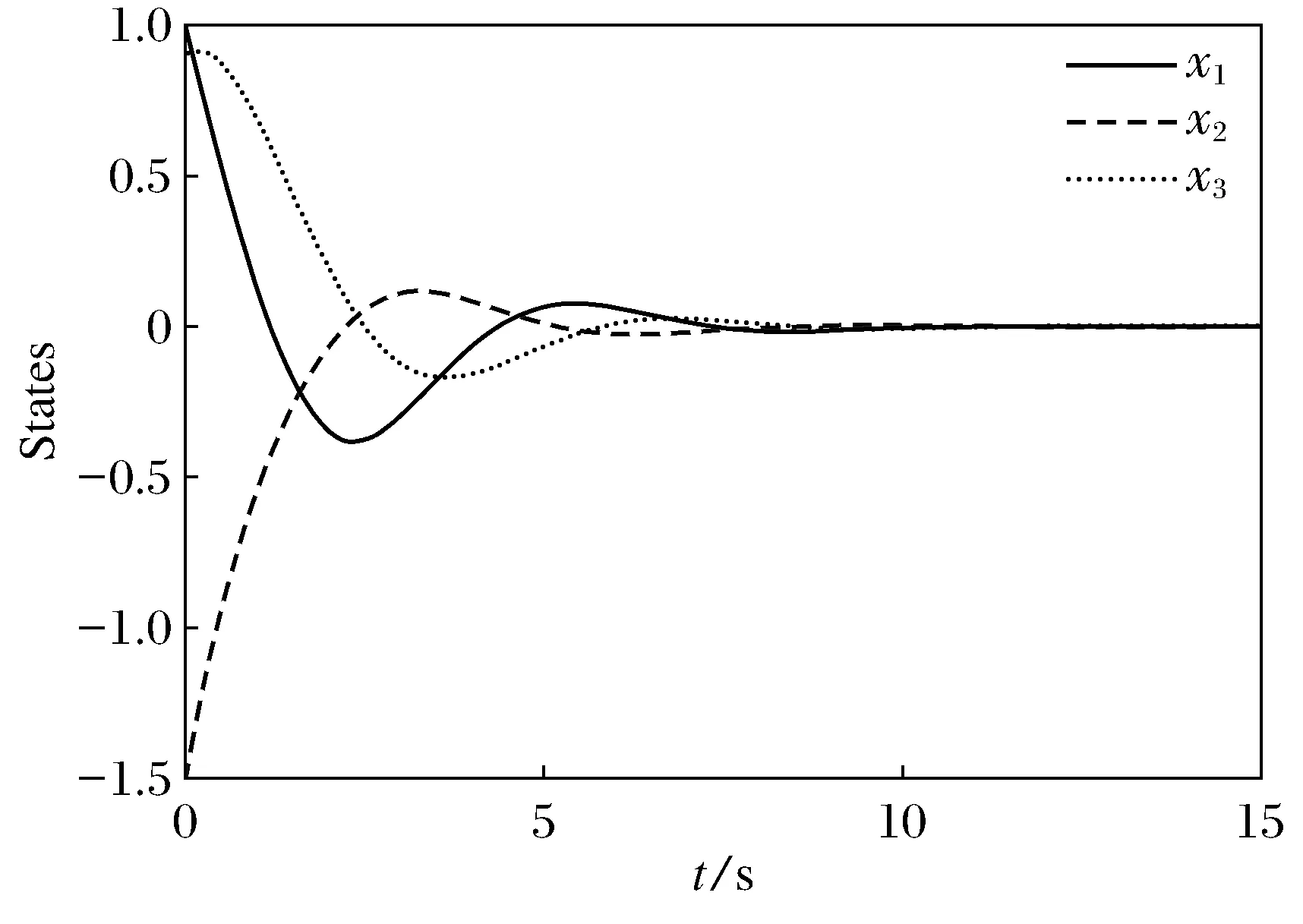
4 结 论

