基于复合滑动窗口数据流动态离散度加权算法

岳晓宁, 丁 宇(沈阳大学 . 师范学院, . 信息工程学院, 辽宁 沈阳 110044)

基于复合滑动窗口数据流动态离散度加权算法

岳晓宁a, 丁 宇b
(沈阳大学 a. 师范学院, b. 信息工程学院, 辽宁 沈阳 110044)

采取实时迭代方式,提出了基于数据流复合滑动窗口模式下动态统计量加权算法.该算法保留了数据流历史数据特征信息,解决了由于数据流长度无界而无法存储全部数据问题,并提高了存储空间有效利用率.通过引入动态统计量,尝试性探索由于抽样理论使得传统统计学不适用于大数据领域的解决思路.算法实验结果表明该算法具有较好性能.

数据流; 滑动窗口; 离散度; 抽象理论; 实时

随着信息技术的不断发展,获取和储存数据信息的能力不断增强,大数据应用越来越普及,很多领域都受到了大数据分析的影响.为了研究和利用这些以指数速度快速增长的数据资源,我们必须研究更有效的数据分析技术[1].许多专家学者为此做了大量的研究工作[2-4],Nature和Science等科学期刊就关于大数据带来的挑战和机遇这个专题相继出版专刊来探讨[5].

在大数据时代研究对象不再是随机抽样,而是全体数据集,通过抽样而使数据量达到传统统计学的统计分析能力范围是很难实现的,它也给传统统计学带来了巨大的挑战.数据流是一种新的大数据模式,数据流数据信息不再是永久储存,具有连续、无限、瞬时等特点.目前有关数据流问题的一些算法往往感兴趣的不是所有的数据,而是最近到达的部分数据,这样得到的计算结果描述的只是最近达到数据信息特征,数据流的历史数据信息特征将被永远丢失,而有些实际问题历史数据信息特征对后面的数据是有一定影响的,所以保留历史数据信息特征也是十分必要的.而针对这个问题的研究目前还极少见.

本文基于按数据输入时间先后顺序定义的复合滑动窗口数据处理模式[6],以均值和方差为例,提出一种结合传统统计学理论,描述大数据特征的动态统计量算法.

1 数据流及其特征

设数据流为按着出现时间递增序列排列的序列集

Ω={s1,s2,…,st,…}.

st为t时刻出现的序列元素.该数据流可以被认为是一个随着时间延续而无限增长且“以高速度输入数据”的动态数据集合.因此对数据流数据的实时存储、实时传输、实时计算等有一定难度.数据流只能对短时间到达的数据进行分析与处理,并且只能做短时间的存储,或一定时间后数据信息永久丢失,所以很难再提取到“历史数据”.对数据流的计算方式不能采用传统的计算模式,是因为数据流数据的本身特点.数据流的连续、无限、瞬时等特点使得在对其进行处理与分析采取的方式是有限和一次性存储与提取、实时快速处理、不精确结果等.

2 数据流滑动窗口离散度算法研究

2.1 复合滑动窗口结构

如果数据收发都会维护一个数据链路层的数据帧序列,这个序列被称作窗口[7].收发两端的窗口都遵守某一规则不断地向前滑动,因此又称为滑动窗口协议.滑动窗口是一种流量控制技术,发送数据一方的窗口规格由数据接收方来控制,其目的是控制数据输入速度过快,导致数据接收端溢出,同时控制数据流拥塞发生.

定义数据流滑动窗口的方法有两种,一是以事先规定好的顺序读取一次数据序列定义的滑动窗口,二是按数据输入时间先后顺序定义的滑动窗口[7].本文以后一种滑动窗口定义方式为例,研究数据流离散度的算法,即以Ω[t-UT:t]为基本滑动窗口,复合滑动窗口Ω[t-nUT:t]数据流Ω的离散度算法,t,UT具有相同单位.

2.2 离散度算法研究

集中趋势和离散趋势是数据描述性分析的重要内容,是数据分布的基本特征.集中趋势反映的是各观测值之间所具有的共同趋势及水平.离散趋势反映的是各观测值偏离中心程度.建立度量集中趋势和离散趋势的统计量模型是描述数据分布特征的常用统计手段.

集中趋势和离散趋势有多种测量方法,每一种方法的选择,可根据数据类型及集中趋势测度值的不同来决定.本文以数据流均值和方差为例,就一维离散型数据流复合滑动窗口实时离散度算法进行研究.

设数据流Ω时刻t所出现时间序列集为{X1,X2,…,Xn(t)},出现序列数据元素总数为n(t),由传统统计学理论定义数据流序列数据均值为

数据流序列数据方差为

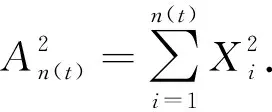
设t0为计时初始时间,在第k个UT时间间隔结束时刻,数据流已出现的时间序列数据总数为nk=n(t0+kUT),则第k+1个UT时间间隔结束时刻,数据流已出现的时间序列数据均值为

该时刻数据流已出现的时间序列数据方差为

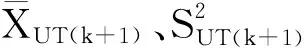
若所有基本滑动窗口内的时间序列集均值和方差都是有界的,令

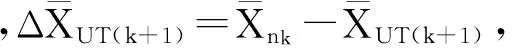
其中,

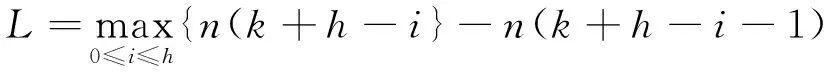
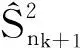
由上述可得出下面定理.

定理1 设复合滑动窗口ΩUT[t-ST:t] 在第k个UT时间间隔结束时刻数据流已出现的时间序列数据元素总数为nk=n(t+kUT).设nk+1-nk,且

(1)n(k+h-i)-n(k+h-i-1)有界;

(2) 数据流序列数据均值与方差有界.

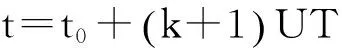
实时方差估计值为

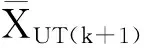
2.3 数据流实时离散度算法性能分析

由式(1)和式(2)可以看出,数据流时间序列数据实时均值是由数据流总体均值和窗口均值的动态加权平均值,且权数恰是所占的动态数据量比重;数据流时间序列数据实时方差为数据流总体方差和窗口方差的动态加权平均值,再加上一个修正项.

该算法的特点与优势:

(2) 本算法采取的是由基本窗口序列数据均值和方差进行动态加权迭代,对数据流的数据信息只在计算基本窗口序列数据均值和方差时提取一次,适应于数据流的特点;

(4) 数据流总体动态均值算法性能不受复合滑动窗口影响,是无误差算法.

数据流总体动态方差算法误差为

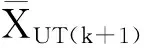
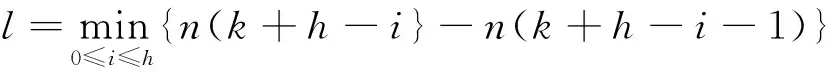
不能过小.

(5) 时间过长的历史数据信息对当前数据信息的影响变小,或消失,即当nk+h过大的时候,数据流较前期的数据信息对现有的数据信息关联度变小,所以可以重新设定计时初始时间t0,重新进行迭代.

3 算法应用

本算法可以应用到大数据技术的许多算法中.以关联规则挖掘算法为例.

关联规则中的一个重要的参数支持度是指X和Y同时出现的频率,即概率;置信度是已经出现X的情况下,出现Y的频率,即条件概率.如果设X和Y为随机变量且取值为1和0,则支持度为随机变量

本算法还可以应用到许多大数据技术与均值和方差相关联的算法中.

4 算法实验结果

本文从某一维匀速数据流中随机取50 000数据元, 设该数据流的数据输入速度为1 000数据元/s. 采用复合滑动窗口数据处理模式, 并设定基本滑动窗口时间间隔UT=1s, 即nk+1-nk=1 000. 运用本文设计的离散度动态加权算法, 可求该数据流动态均值和方差结果. 表1为第4个到第18个滑动窗口所采集的数据计算结果.

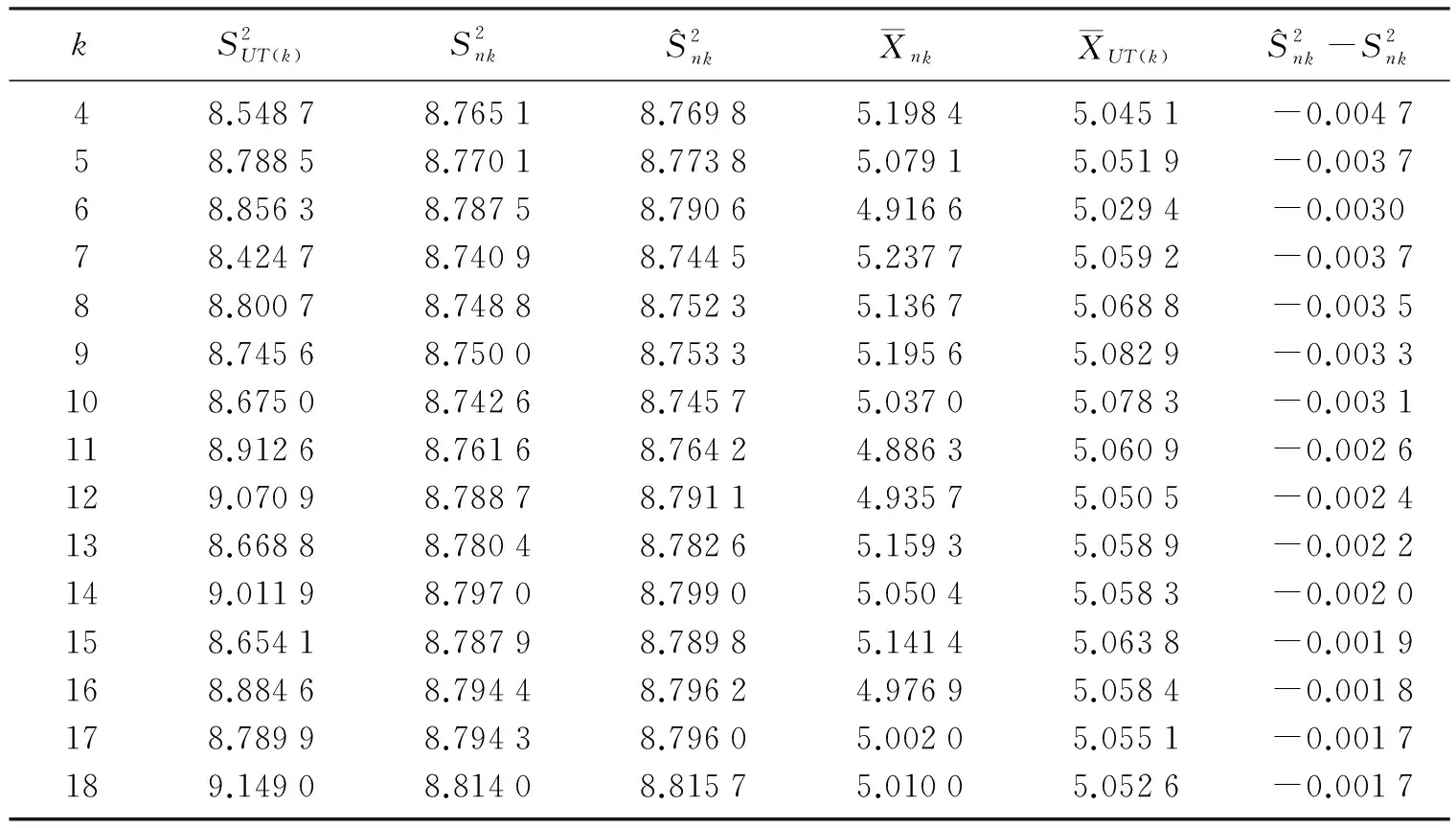
表1 离散度动态加权算法计算结果Table 1 The results of dynamic weighting algorithm for dispersion

图1显示方差动态加权算法估值误差在前几个基本滑动窗口的计算结果还有些波动,随着滑动窗口的移动,误差趋于零的趋势显著.

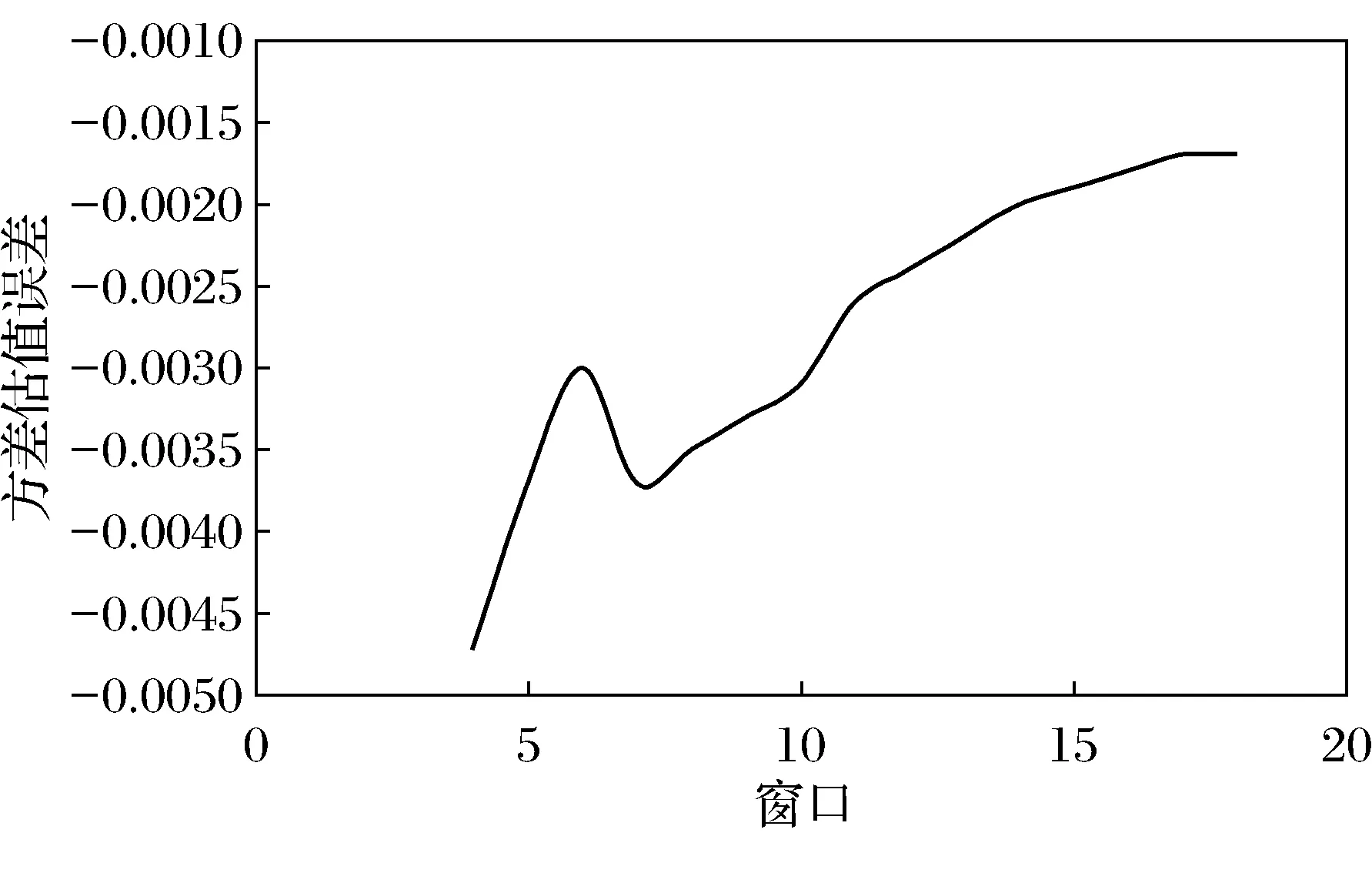
图1 方差估值误差Fig.1 The estimation error of valuation

5 结 论

传统统计学的抽样理论已不适应大数据时代的数据特征,所以传统统计学要想在大数据时代下继续发挥作用,必须改进和发展适应大数据新时代的“抽样”理论.本算法的提出对传统统计学的抽样理论重构有非常重要的理论意义.

[1] 覃雄派,王会举,杜小勇,等. 大数据分析: Rdbms与Mapreduce的竞争与共生[J]. 软件学报, 2012,23(1):32-45. (QIN X P, WANG H J, DU X Y, et al. Big data analysis: competition and symbiosis of Rdbms and Mapreduce[J]. Journal of Software, 2012,23(1):32-45.)

[2] 陈冬玲,曾文. 频繁模式挖掘中基于CFP的应用模型[J]. 沈阳大学学报(自然科学版), 2015,27(4):296-300. (CHEN D L, ZENG W. Application model based on CFP in mining frequent patterns[J]. Journal of Shenyang University(Natural Science), 2015,27(4):296-300.)

[3] 王群,朱小英,关郁波. 大数据背景下审计工作面临的挑战与启示[J]. 沈阳大学学报(社会科学版), 2016,28(1):35-37. (WANG Q, ZHU X Y, GUAN Y B. Challenge and enlightenment for auditing work in big data age[J].Journal of Shenyang University (Social Science), 2016,28(1):35-37.)

[4] Committee on the Analysis of Massive Data, Committee on Applied and Theoretical Statistics, Board on Mathematical Sciences and Their Applications, et a1. Frontiers in massive data analysis[M]. Washington: National Academies Press, 2013.

[5] 靳小龙,王元卓,程学旗. 大数据的研究体系与现状[J]. 信息通信技术, 2013,7(6):35-42. (JIN X L, WANG Y Z, CHENG X Q. Research system and status of big data[J]. Information and Communication Technology, 2013,7(6):35-42.)

[6] ZHU Y, SHA S D. StatStream:statistical monitoring of thousands of data streams in real time[C]∥VLDB’02 Proceedings of the 28th international conference on Very Large Data Bases, 2002:358-369.

[7] 钟颖莉,李金宝,王伟平,等. 数据流上的复合滑动窗口聚集算法[J]. 计算机工程与应用, 2006,42(14):187-191. (ZHONG Y L, LI J B, WANG W P, et al. Aggregate algorithms of compound sliding window over data streams[J]. Computer Engineering and Applications, 2006,42(14):187-191.)

【责任编辑: 肖景魁】

Dynamic Dispersion Weighted Algorithm for Data Stream Based on Compound Sliding Window

YueXiaoninga,DingYub

(a. Normal School, b. School of Information Engineering, Shenyang University, Shenyang 110044, China)

Using the real time iterative method, a dynamic statistical weighted algorithm based on the compound sliding window over data streams is proposed. This algorithm preserves the characteristic of historical data of the data stream, and solves the problem that the data stream cannot store all data due to the unbounded data stream length and improves the effective utilization rate of the storage space. Through the introduction of dynamic statistics, trying to explore the solution that the sampling theory makes the traditional statistical method is not suitable for the field of big data. The simulation results show that the algorithm has good performance.

data stream; sliding window; discrete degree; abstract theory; real time

2016-12-06

国家自然科学基金资助项目(61503274); 沈阳市科技计划项目(F14-129-9-00).

岳晓宁(1962-),女,辽宁沈阳人,沈阳大学教授,博士.

2095-5456(2017)01-0078-04

O 236

A