高阶残差修正GM(1,1)区间预测模型及其应用
张 磊,孙长青
(1.中国人民解放军66021部队,天津 301900; 2.沈阳工程学院 机械学院,沈阳 110136)
【基础理论与应用研究】
高阶残差修正GM(1,1)区间预测模型及其应用
张 磊1,孙长青2
(1.中国人民解放军66021部队,天津 301900; 2.沈阳工程学院 机械学院,沈阳 110136)
提出了一种Markov高阶残差修正GM(1,1)区间模型,在GM(1,1)模型的基础上对拟合数据残差项的绝对值运用Markov模型进行数据拟合,通过将残差项叠加的方式逼近数据真实值。根据残差项的正负状态构建了预测区间,并通过数值模拟论证了预测区间的适用范围与合理性,运用Markov模型对预测区间进行了修正和改进,给出了Markov高阶残差预测区间的表达式。分析结果表明,模型弱化了灰色发展系数的取值条件,并且计算修正残差的阶数越高,预测区间结果可靠性越高,避免了根据概率大小选择预测结果所产生的预测风险,提高了预测结果的可靠性。
GM(1,1)模型;残差修正;Markov模型;需求预测
随着我国“软科学”的逐步发展和普及,运用各类数学模型进行需求预测的方法在决策领域发挥着日益重要的作用。与此同时,对于模型的精度和合理性方面的要求也越来越高。
基于传统概率统计理论所构建的数学模型往往要求数据变化存在某种规律或者服从某种概率分布,这使预测变得非常困难。以新型装备的备件需求量为例,因其投入使用速度的加快,以及装备使用环境的复杂性,影响备件需求预测数量的因素非常之多,很难从中找到数据的变化规律。灰色GM模型能够较好地处理“小样本”、“贫信息”等不确定性系统的预测问题[1],在各个领域得到广泛应用[2-4]。但当数据变化跳跃性较大时,GM(1,1)模型预测结果会产生较大误差。不少学者通过修正GM(1,1)模型产生的残差,提高GM(1,1)模型的预测精度,特别是Markov模型,具有无后效性的优点,非常适合预测GM模型残差的变化,因此近几年来相关研究比较活跃,如王秋萍等[5]将Markov残差修正的灰色GM(1,N)模型运用于预测粮食产量,宋强等[6]运用Markov修正模型预测机床切削力等。在运用GM(1,1)模型做备件和维修器材需求预测方面也有类似研究,赵平等[7]提出了运用Markov残差修正的灰色GM(1,1)模型预测装备维修器材消耗情况,王铁宁等[8]运用加权Markov修正模型对预测结果进行修正,均取得非常理想的效果。
然而,运用Markov相关模型解决GM模型产生的残差,并最终得出预测值的方法却存在部分缺陷。比如,Markov模型要求将GM模型产生的残差人为地划分状态区间,其划分标准不一将在较大程度上影响模型精度[8-9]。同时,Markov模型最终得到的仅仅是其结果数值处于某一状态的概率值,在取得概率较大状态结果的同时,忽略了其他状态结果的可能性,甚至有可能使预测结果更加偏离真实值,为决策增加风险因素。单一的预测结果不利于为多样性决策提供有力支撑。
因此,本文在“区间预测”思想的基础上[10],通过求解高阶残差对拟合值进行修正并构建预测区间,通过数值模拟论证了GM(1,1)高阶残差区间模型在提高预测精度上的有效性,运用Markov模型对模型进行了改进,给出了高阶残差预测区间的表达式。为保障决策提供了较为“大胆”和相对“保守”的预测结果,有效提高了运用Markov模型修正GM(1,1)预测结果的可靠性。
1 GM(1,1)模型的建立
1.1 模型基本原理
由定义可知,{x(0)(k)}为原始序列,GM(1,1)模型的可以描述为
(1)

1.2 边界条件的确定
(2)
2 残差修正区间模型
2.1 残差修正模型
根据原始数据序列和GM(1,1)模型的拟合值序列,可以定义残差序列
(3)
由于式(3)为绝对值形式,在残差修正GM(1,1)模型中,不同时滞下残差修正模型可以表达为
(4)

(5)

a1和b1分别为拟合1阶残差时的系数。
2.2 高阶残差GM(1,1)区间模型
同理,在对GM(1,1)模型拟合的数据进行1次残差修正后,为提高拟合精度,仍然可以在修正后的序列基础上继续进行残差拟合修正,即
(6)
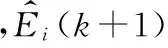
由式(4)可以看出,残差的正负影响着预测值的准确与否,将式(5)中的δ(k+1)带入式(6),便得到了高阶残差修正模型。在理想状况下,这种模型拟合精度非常高(这一点在实例分析中说明)。因此,从决策的实际角度来看,可以考虑预测的真实值落在某一区间:

2.3 数值模拟
分别令a=0.1,0.2,…,0.7,取k=1,2,…,10,按照x(k)=eak构造指数序列,将前6位数作为已知序列,运用式(1)和式(2)进行计算,并运用式(3)~式(6)构造预测区间。将后4位数作为预测对比值,计算结果如表1所示。

表 1 1阶残差区间预测模型模拟

2.4Markov修正区间模型
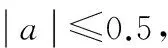
当序列变化的幅度较大时(即R0较大时),便会造成灰度区间过大和侧重方向无法体现等问题。
根据残差变化情况判断,其正负变化过程存在Markov链的变化特点,于是便可以根据残差的正负关系划分Markov链的状态:将残差符号为正时的状态定义为状态1,残差符号为负时的状态定义为状态2。在预测时,根据不同状态概率的大小取定符号,即
(7)
其中,pk+1(j)为在k+1时刻,处于状态j的概率,j=1,2。
由式(7)可知,在实际预测时,不能忽略δ(k+1)取不同值的可能性,特别是pk+1(1)与pk+1(2)相差不大时,预测便存在“赌博”的特性。然而区间形式的预测结果却能很好地弥补这一缺陷,可以将1阶残差预测区间改进为
这一数值反映了原始数据跳跃变化的幅度大小,由模拟区间可以看出,当数据跳跃变化的幅度逐渐减小时,预测区间将逐渐缩短,预测区间和拟合值都将收缩为传统GM(1,1)模型的预测值。
同时显然有
ipk + 1(2) +ipk + 1(1) = 1
当考虑1阶残差修正的情况下,由式(8)可知,当1pk + 1(1)→1时,有1pk + 1(2)→0。此时变为
当1pk + 1(2)→1时,有1pk + 1(1)→0。此时模拟空间变为
此时,模拟区间预测结果类似于传统模型的预测结果。
3 实例分析
以文献[8]中的装备备件统计数据为例,2004—2013年备件S需求数量序列为
x(0)={86,91,102,91,103,101,93,94,107,99}
因为该数据引自文献[8],故在此不再进行级比检验。同时,为便于进行数值说明,保留小数点后4位小数。
3.1 3阶残差GM(1,1)模拟
将式(9)代入式(1)~式(6),计算前3阶残差修正模型,计算结果如表2所示。
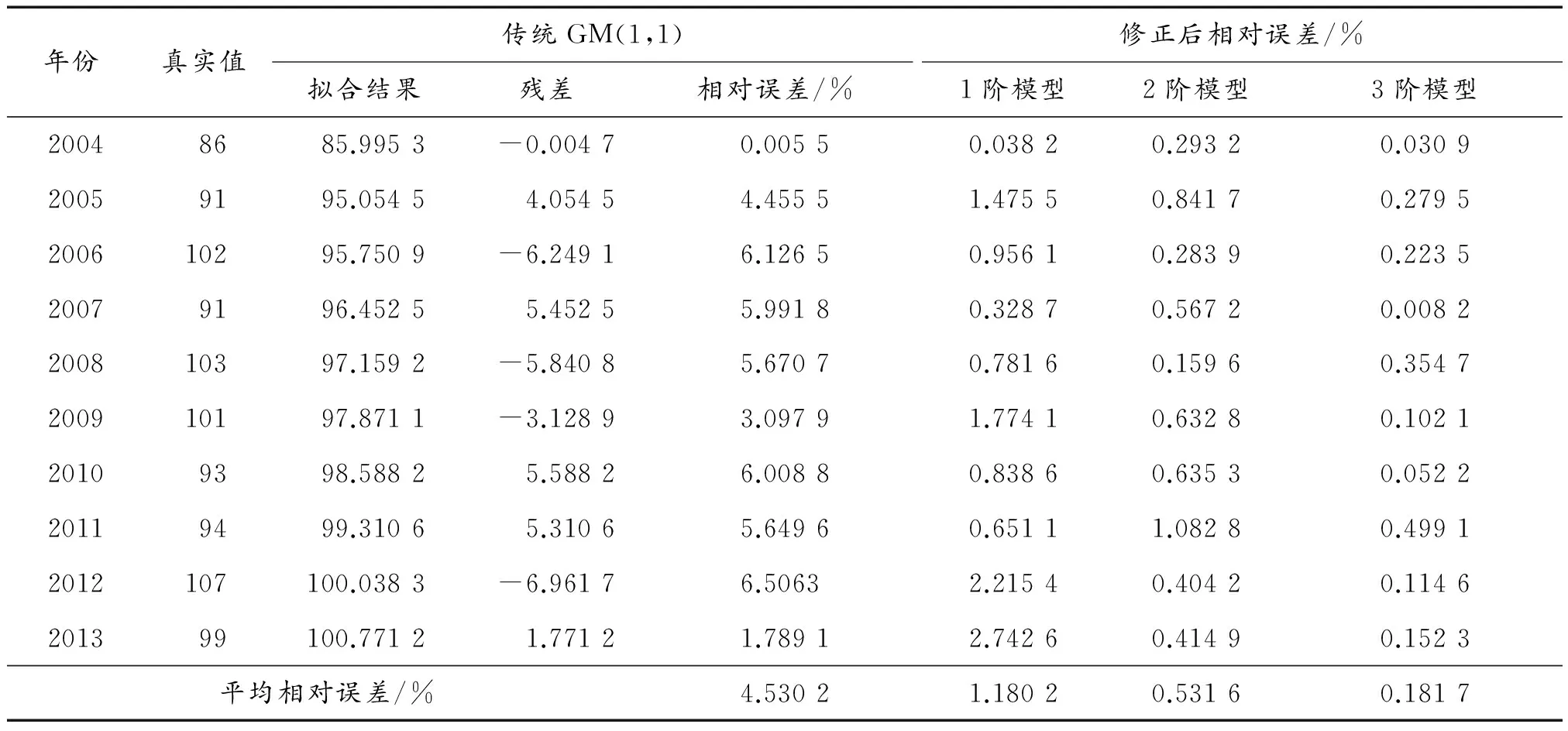
表2 GM(1,1) 模型拟合结果以及各阶残差修正拟合结果
由表1可以看出,由于数据变化幅度较大,传统GM(1,1)的相对误差较大,达到4.53%。同时可以看到,残差计算阶数越高,平均相对误差越小,拟合值与真实值之间就越接近,从备件需求数量拟合的角度来看,3阶残差模型拟合出的数值几乎与真实值完全一致。因此可以认为,只要阶数m足够大,且模型发展系数a无较大变化,即在没有新的突变因素的干扰下(如设备操作环境没有大幅度变化、设备操作方式没有大幅度改变等),以m阶残差修正后的GM(1,1)区间必将涵盖序列在k+1时刻的真实值,即:[93.856 6, 109.162 7]。
然而,这一区间不能体现决策时残差正负的倾向性,而且区间长度太长,无形当中降低了决策的可操作性,因此采用Markov模型预测残差正负的变化情况。
3.2 Markov修正区间
如前文所述,将残差符号为正时的状态定义为状态1,残差符号为负时的状态定义为状态2。根据表2中各阶残差变化的次数统计并建立一步状态转移矩阵:
初始状态概率为:
其中,iP为第i阶残差的一步状态转移矩阵。再由切普曼-柯尔莫哥洛夫方程计算各步长的状态转移矩阵,最后计算不同时刻下的状态概率,计算结果如表3所示。

表3 各阶残差计算不同状态概率的计算结果
计算可得预测区间为:[98.034 9, 105.687 9]。
因此在这个预测区间里较大胆的预测值为98,而较为保守的预测值为106。
4 结论
2) 当数据跳跃变化的幅度逐渐减小时,预测区间将逐渐缩短,预测区间和拟合值都将收缩为传统GM(1,1)模型的预测值。当其中一个状态对应的转移概率无限接近于1时,该模型将退化为类似传统模型。
3) 在无突变因素影响的前提下,计算残差阶数越高,数据拟合的平均相对误差就越小。从实际运用的角度来看,如果计算阶数足够高,相对误差可以忽略不计。在没有新的突变因素的干扰下,以高阶残差修正后的GM(1,1)区间必将涵盖序列预测的真实值。
4)区间式的预测结果很好地避免了根据概率大小选择预测结果所产生的预测风险,同时为决策提供了较为大胆和相对保守的预测值,提高了预测结果的可靠性。
[1] 刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2014.
[2] 资道根.基于灰色GM(1,1)模型的跨境电子商务发展前景预测分析[J].数学的实践与认识,2015,45(1):96-105.
[3] LIU Sifeng,Hu Mingli,Forrest Jeffrey,et al.PROGESS OF GREY SYSTEM MODELS[J].Transaction of Nanjing University of Aeronautics and Astronautics,2012,29(2):103-111.
[4] 郭敏,蓝金辉,李娟娟,等.基于灰色残差GM(1,N)模型的交通数据流恢复算法[J].交通运输系统工程,2012,12(1):42-47.
[5] 王秋萍,闫海霞,闫建波.Markov残差修正的灰色GM(1,N)模型在粮食产量预测中的应用[J].西安理工大学学报,2009,25(3):347-350.
[6] 宋强,朱艳芳,李华.基于灰色残差修正模型的机床切削力预测与仿真[J].机械工程与自动化,2008(6):47-49.
[7] 赵平,刘宝平,黄栋.一种用于装备维修器材消耗预测的灰色残差修正模型[J].四川兵工学报,2014,35(5):62-65.
[8] 王铁宁,朱域,陈晓晨.基于灰色加权马尔科夫的备件需求预测[J].装甲兵工程学院学报,2015,29(3):8-13.
[9] 李雪梅.灰色关联分析与GM(1,1)模型优化的研究与应用[D].南京:南京航空航天大学,2011.
[10]吴利丰,刘思峰,闫书丽.区间灰数序列的灰色预测模型构建方法[J].控制与决策,2013,28(12):1912-1915.
[11]刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践,2000,20(5):121-124.
(责任编辑 杨继森)
Higher-Order Residual Error Corrected GM(1, 1) Interval Prediction Model and Its Application
ZHANG Lei1, SUN Chang-qing2
(1.The No. 66021stTroop of PLA, Tianjin 301900, China;2.School of Mechanical and Engineering, Shengyang Institute of Engineering, Shengyang 110136, China)
The interval prediction GM(1, 1) with Markov higher order residual error correction was proposed. Based on prediction results of GM(1, 1), the absolute residual error was calculated by markov, and the true value was approximated by superposition of residual error items. the prediction interval was constructed, and the suitable range and rationality of model were discussed. Finally the Markov model was used to improve the prediction interval model and the equation was given and discussed. The model softens the restrict range of development coefficients; and the higher order residual error correction is used, the less mean relative error is obtained, and the more reliable the prediction result is. The prediction risk caused by which prediction result is selected according to its state probability is avoided; and the reliability of prediction is improved.
GM(1, 1) model; residual error correction; Markov model; demand prediction
2016-09-27;
2016-10-25
国家自然科学基金资助项目(51371173)
张磊(1983—),男,助理工程师,博士,主要从事装备精确保障研究;孙长青(1978—),男,讲师,博士,主要从事机械强度和合金材料研究。
10.11809/scbgxb2017.02.039
张磊,孙长青.高阶残差修正GM(1,1)区间预测模型及其应用[J].兵器装备工程学报,2017(2):177-181.
format:ZHANG Lei, SUN Chang-qing.Higher-Order Residual Error Corrected GM(1, 1) Interval Prediction Model and Its Application[J].Journal of Ordnance Equipment Engineering,2017(2):177-181.
TJ01;N941.5
A
2096-2304(2017)02-0177-05

