五度圈中的音、音列、音阶及其数理关系
杜亚雄
摘要:对五度圈中的音、音列、音阶及其内在的数理逻辑关系进行探讨,指出了从五度圈中相邻音中所取的数量及其作为不同音级的可能性之间和所含“宫音”数量之间的规律。前者可用“鱼合八”“鱼合七”“鱼合六”加以说明,后者则可用“x(音列或音阶中音的数量)-4=宫音数量”的公式进行概括。
关键词:五度圈;音列;数理逻辑
中图分类号:J613.6 文献标识码:A 文章编号:1004-2172(2016)04-0023-05
五度圈又称“五度循环”(circle offifth),即按五度关系,从C音开始,沿顺时针或反时针方向,依次历经其他11个音,最后回到C音的圈。顺时针是往属方向进行上五度循环,反时针是往下属方向进行下五度循环。如下图所示:
如果用五度相生律,从C音开始经历11个音之后,所生出的#B比C高一个古代音差,即24音分,只能构成“五度螺旋”(spiral of fifth),不能循环,因此中国古代之始发律“黄钟”不能还原。朱载堉为使“黄钟”能够还原,发明十二平均律,并在《乐学新说》一书中首先提出了五度循环的原理。
《尚书》中有“同律度量衡”的说法,《吕氏春秋》中指出:“音乐之所由来者远矣:生于度量,本于太一。”可见先民很早就注意到了音乐和数学之间的密切关系。十二平均律的发明不仅是音乐学的成果,也是数学的成果,为我们从数理逻辑方面探索乐理中的一些问题开辟了广阔道路。然而长期以来,我国音乐理论界却忽视了从这方面进行研究,把一些从数理逻辑上看根本不是问题的问题搞成了问题,且争论不休,得不出结论。如20世纪80年代,黄翔鹏先生提出“同均三宫”的理论后,音乐学界争论激烈。有人认为这一理论的提出对我国传统音乐研究和基本乐理建设都有很深远的意义。也有人认为“同均三宫”根本就是“假象和错觉”。目前,音乐学界对此尚未取得共识。
数理逻辑是数学和逻辑学相结合的综合学科,它用数学方法研究形式逻辑问题,并将推理过程用数学公式进行运算,从而得出结论。本文尝试采用数学方法对五度圈上的音、音列、音阶的关系进行探讨,试图证明一些乐理的基本原理。为便于讨论,首先说明有关音、音列、音阶和“宫”的概念。
郑玄说:“宫商角徵羽,杂比曰音,单出曰声”可见在汉代,单个音级称为“声”,若干“声”放在一起称为“音”。现代汉语中仍保留了这种用法,如在“五声音阶”和“七声音阶”等词组中,“声”指单个音级,“音”由数“声”构成。现代汉语中的“音”也可指单个音级,如“宫音”“商音”,还可以指某一类曲调,如“花音”“苦音”“欢音”“哭音”。本文中的“音”指单个音级。
欧洲乐理认为多于一个音级,便能构成音阶,有二声音阶(ditonic scale)、三声音阶(tritonic scale或trichord)、四声音阶(tetratonic scale或tetrachord)的概念。因有“五行学说”的传统,我国音乐理论界普遍认为够“五声”才能叫“音階”,只有二个、三个或四个音的组合称为“音列”,本文亦将它们称为“音列”。
我国音乐理论界一般承认“五声音阶”和“七声音阶”,至于“六声音阶”是不是一个真实、独立存在的概念,则有争论。笔者认为“六声音阶”是客观的存在,本文将讨论“五声”“六声”和“七声”三种不同的音阶。
中国乐理中所使用“宫”字的意义通常有三:(一)阶名之一,即“宫声”或“宫音”,它历来被视为众“音”之首,被称作“音主”,在中国音乐中具有重要地位。无论是五声还是七声音阶,一旦宫音的高度位置确定,其它各音(如商、角等)的高度也就都确定下来了。本文中称“宫”的这层意义为“宫音”。“宫音”统领着下面所说“宫系”。(二)自起始律到相生第六次所得的那一律,七个律位排成的七声音阶构成“一宫”,通常以起始律命名,如“黄钟宫”“林钟宫”等。由于我国古代以“正声音阶”为标准,今天以西洋大调式结构相同的“下徵音阶”为标准,如果将“黄钟”相当于西洋音名中的“C”,古代的“黄钟宫”相当于今天的“G宫”下徵音阶而不是“C宫”正声音阶。(三)指与第二项“宫音”高度相同的各五声或七声调式构成的“宫系统”。后两个层面上的“宫”都具有调高的意义,本文都称为“宫系”。正如前面说的,“宫系”由“宫音”统领,没有“宫音”,也就没有“宫系”
一
五度圈中每个“音”在音列、音阶中的地位,依靠它与其他“音”的关系决定,其中存在着严格的数理关系。
在五度圈上任取一个“音”,它便可能是五声音阶或六、七声音阶中的任何一个音。在五声音阶中有五种可能性,从首调唱名法讲(下同),可能是do,可能是re,也可能是mi、sol或la。在六声音阶中有六种可能性,七声音阶中的可能性有七种,可能是do,可能是re,也可能是mi、fa、sol、la或者是ti。此时,不可能明确它是“宫音”还是其他任何音。在用五度圈上相邻的音构成两音列、三音列和四音列三种情况下,“宫音”也是不可能确定的。
如果在五度圈上取相邻的两个音,这两个音之间只能构成纯五度及其转位纯四度的音程。此时,比起只有一个音来,当作不同音级的可能性便减少一种。如取“C-C”两音,在五声音阶中有“do-sol”“la-mi”“sol-re”“re-la”四种可能性。在六声音阶中多一种可能性,可能是“fa-do”,也可能是“mi-ti”。在七声音阶中就又多了一种可能性,即“fa-do”和“mi-ti”都有。
如果在五度圈上取相邻的三个音,这三个音之间可以构成纯五度、纯四度和大二度、小七度的音程。当作不同音级的可能性比“二音列”更少一种。如取“C-G-D”三个音,在五声音阶中有“do-sol-re”“sol-re-la”“re-la-mi”三种可能性。在六声音阶中也多一种可能性,即可能是“fa-do-sol”,而在七声音阶中就又多了一种可能性,即可能是“la-mi-ti”。黎英海先生在《汉族调式及其和声》一书中以陕北民歌《绣荷包》为例,指出其中的“g-c-d”三个音可能是“徵-宫-商”、也可能是“商-徵-羽”或“羽-商-角”。因为他认为“在任何调式中宫音总不可省去”,所以说《绣荷包》是徵调式。其实在为这一曲调配和声时,也不妨把它看成是羽调式或商调式,这样选择性多些,色彩也会更为丰富。
如果在五度圈上取相邻的四个音,它们之间可以构成的音程是纯五度、纯四度、大二度、小七度、小三度、大六度,比起“三音列”来,作为不同音级的可能性又要更少一种。如取“C-G-D-A”四个音,在五声音阶中有“do-sol-re-la”“sol-re-la-mi”两种可能性。在六声音阶中多一种可能性,七声音阶中比六声音阶还多一种可能性。黎英海先生曾以一首由G-A-C-D四个音构成的、长江流域的山歌为例,并指出因为曲调中“没有出现角音”,“可能是徵调,也可能是商调”。按照黎先生“宫音不能省去”的理论,这首歌是“徵调式”。然而,如果在配和声时,把它商调式来处理,也没有什么不妥之处。
如果在五度圈上取相邻的五个音,在第一个音和第五个音之间就会形成一个大三度,这大三度音程就形成了中国乐理中的“宫一角关系”。此时,這五个音作为不同音级的可能性比“四音列”更少一种,在五声音阶的情况下,只有“do-re-mi-sol-la”一种可能性。在六声音阶中多一种可能性,七声音阶中比六声音阶还要多一种。这时,也只有在这时,“宫音”的位置就明确了。
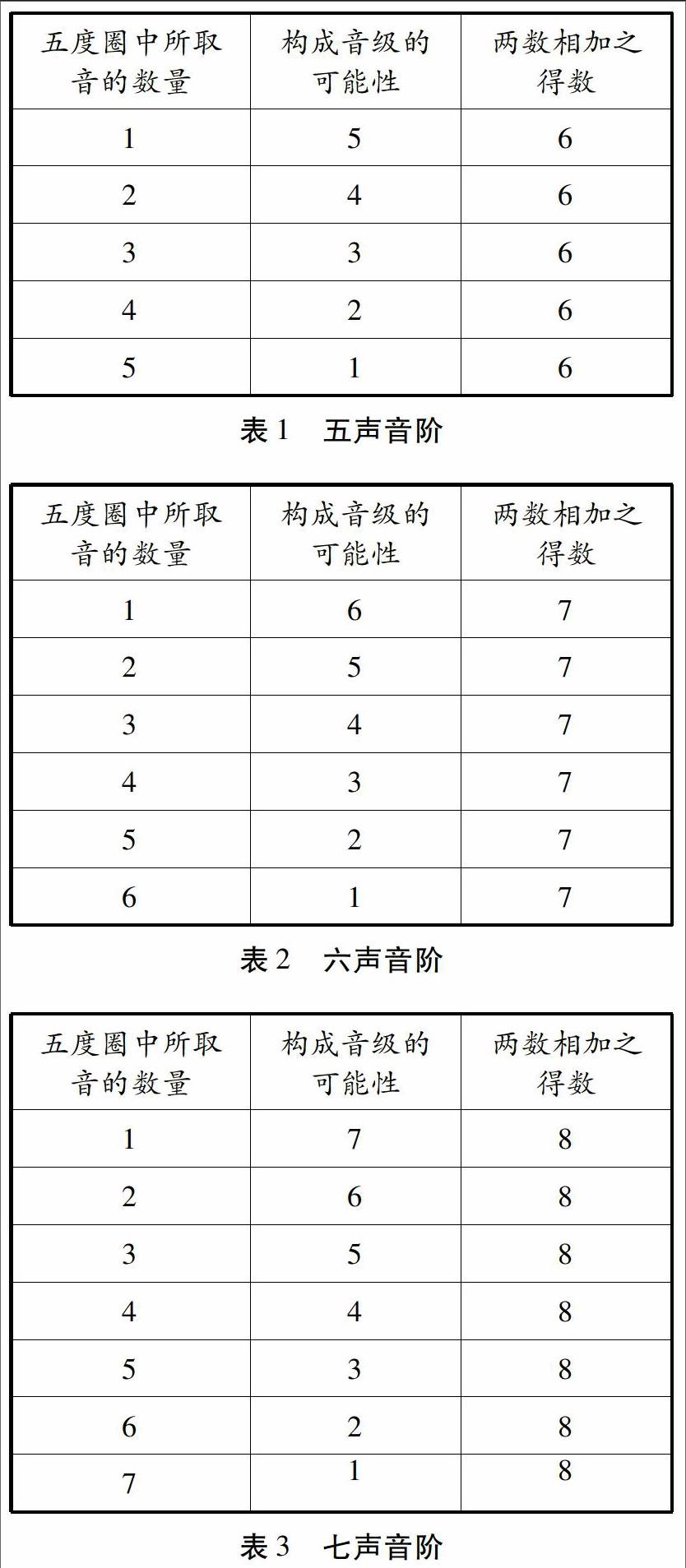
至此,我们便可以发现在五度圈中所取音的数量及其作为不同音级可能性之间的数理逻辑关系,即:音的数量及作为不同音级的可能性的数量相加为音阶中的音级数加一。若为七声音阶,其得数应为“8”,六声音阶应为“7”,五声音阶是“6”。如表1、2、3所示:
在我国传统音乐中,有一种称为“鱼合八”的结构形式,每个乐句都有八个谱字,分两个部分,第一部分递增,谱字分别为1-3-5-7,第二部分递减,谱字数分别为7-5-3-1,两个部分相加总是8,故名“鱼合八”。如谱例1所示:
谱例1
表1、2、3中显示出的数理逻辑结构与“鱼合八”一致,在七声音阶的条件下为“鱼合八”,六声音阶为“鱼合七”,而五声音阶则是“鱼合六”。
二
在五度圈中取相邻的音构成音列、音阶及其所含的“宫音”的数量,也有严格的数理逻辑关系,而且和上述五度圈中所取音的数量及构成音级的可能性密切相关。正如前文所述,如果在五度圈中取相邻的四个音,它们之间不能构成“宫一角”关系,因此会有“do-sol-re-la”“sol-re-la-mi”两种不同的解释。然而在五度圈上取相邻的五个音,在第一个音和第五个音之间就会形成一个大三度,这大三度音程就形成了中国乐理中的“宫-角关系”,这样“宫音”的位置就定下来了,在五声音阶的条件下,便只能有一种可能性了。
如果在五度圈中取相邻的六个音,在第一个音和第五个音之间和在第二个音及第六个音之间就能构成两对“宫-角”关系,便可能有两“宫音”和与之相应的两个不同的“宫系”存在于这个六声音阶中,如“c-g-d-a-e-b”即可能是“do-re-mi-fa-sol-la”(G宫)也可能是“do-re-mi-sol-la-ti”(C宫)。这两种六声音阶中的第一种在欧洲乐理中称为“自然六声音阶”(natural hexachord),第二种则称为“硬六声音阶”(hard hexachord)。
谱例2是一首著名的蒙古族民歌,从谱面上看是六声音阶,笔者1987年在匈牙利李斯特音乐学院教学时,曾要求同学们演唱它。匈牙利采用首调唱名法,故同学们将第一小节第一个音符唱“la”。在我国,用首调唱名法演唱第二行时,仍按两个升号的调来唱,前两个音符唱“do-fa”。匈牙利学生却把第二行的第一、二个音符都唱成“do”,因为按照欧洲的“首调唱名法”,从这一小节第二个音起,已转入一个升号的调,必须要改换唱名法。匈牙利学生的唱法说明,用五度圈中取相邻的六个音构成的六声音阶,按照欧洲乐理的规范,也可以有两个“宫音”和两个“宫系”。
谱例2
如果在五度圈上取相邻的七个音,在第一个音和第五个音、在第二个音和第六个音和在第三个音和第七个音之间就会形成三个大三度。这三个大三度音程都可以形成“宫一角关系”,在这个七声音阶中便会有三个“宫音”和它们所统领的“宫系”。如“c-g-d-a-e-b-#f”,即可能是“do-re-mi-fa-sol-la-ti”(G宫)也可能是“do-re-mi-#fa-sol-la-ti”(C宫)还可能是“do-re-mi-fa-sol-la-bti”(D宫)。这三“宫系”之间“音主”的位置必然是五度圈上的第一、二、三音,它们之间的关系也必然是纯五度、纯四度和大二度,其实这就是“同均三宫”。关于什么是“均”,黄翔鹏先生说:“在‘五度圈的连续音高序列中摘取七律(古书中叫做‘以七同其数)构成音阶(古书中也把七声音阶称做‘七律),这七个律高所构成的绝对音高位置与各律间相对的音程关系的总和就是‘均。这个定义如果不好理解,我们只好简单化地说,‘均就是七律在‘五度圈中的位置。”
如果在五度圈上,任选连续的8个音,就可以构成4个大三度音程,它们分别处于第一个音和第五个音、第二个音和第六个音、第三个音和第七个音、第四个音和第八个音之间。如果任选连续的9个音,就可以构成5个大三度音程,它们分别处于第一个音和第五个音、第二个音和第六个音、第三个音和第七个音、第四个音和第八个音、第五个音和第九个音之间。如果任选连续的10个音,就可以构成6个大三度音程。选11个音,就可以构成7个大三度音程。其内在的数理逻辑是五度圈中所取音的数量减去数字4,便构成能够形成“宫音”和“宫系”的数量。如表4所示:
如果在五度圈上,任选连续的11个律位,可构建7个“宫系”。最后生成的5律,在十二平均律的条件下,转换为等音,就可以建立12个“宫系”。这12“宫系”,就是在西方乐理中12个调。在每个上面建立一个大调和一个小调,就是以图一中显示的那些音为主音的24个大小调。
从表4中不难看出,从五度圈上所取的音的数量和能构成“宫音”及其统领的“宫系”的数量成正比,三个数字之间的关系是:“音列”所包含的“音”数量减4,就得到这些“音”可能构建的“宫系”的数量。
小结
“鱼合八”“鱼合七”“鱼合六”以及“同音列数宫系”的现象应当是放之四海而皆准的,古今中外,在采用五度相生律的各民族的音乐中,应当没有、也不会有例外。
从五度圈中所取的“音”的数目和它们在音列、音阶中所充当音级的可能性为反比。所取的“音”的数目越少,可能性越多。所取的“音”的数目越多,可能性则越少。
从五度圈中所取的“音”的数目和出现“宫音”以及由其所统领的“宫系”数目之间为正比,“音”的数目越多,“宫音”的数目越多;低于四个音,“宫音”便不能确定,“宫音”需要有5个音才能确定,之后每增加一个音,就增加一个“宫音”。黄翔鹏先生提出“同均三宫”理论,也应当被包含在“同音列数宫系”的法则中,“同均三宫”的理论只涉及了一个在五度圈上取7个音的情况,并没有论及取6个音或超过7个音时的情况。
既然“鱼合八”“鱼合七”“鱼合六”以及“同音列数宫系”的现象在中国音乐和欧洲音乐中都存在,就应当在乐理课中介绍,这对音乐理论建设和音乐创作实践都有会有所裨益。
责任编辑:李姝