基于改进布谷鸟算法的随机最优潮流
周 前,卫 鹏,刘超君
(1. 江苏省电力试验研究院有限公司,江苏南京211103;2. 国网重庆市电力公司,重庆402260)
基于改进布谷鸟算法的随机最优潮流
周 前1,卫 鹏1,刘超君2
(1. 江苏省电力试验研究院有限公司,江苏南京211103;2. 国网重庆市电力公司,重庆402260)
面对各种智能算法在优化问题的应用中出现的问题,提出一种基于量子计算和混沌局部搜索的布谷鸟算法。混沌局部搜索采用切比雪夫映射产生的混沌数列,以产生的新最优个体替代原始最优个体,并利用量子旋转门更新其余个体,达到更快收敛并跳出局部解的效果。以随机最优潮流问题作为修正布谷鸟算法的应用场景,考虑分布式电源和负荷的随机性,建立随机最优潮流的机会约束模型,机会约束的处理采取修正变量上下限的方式。以IEEE33节点为算例,对比了4种不同智能算法的计算结果和收敛情况,验证了修正的布谷鸟算法在随机最优潮流中收敛速度快,收敛结果好,稳定性好的特点。
量子计算;混沌局部搜索;布谷鸟算法;随机最优潮流;机会约束规划
0 引言
最优潮流是典型电力系统的优化问题,首先由Carpentier提出。由于最优潮流是确定性的问题,如确定性负荷、确定性电源出力、确定性网络结构。但是,由于近年来分布式电源的接入,导致系统中出现了大量不确定性参数[1],传统的最优潮流模型已经无法精确模拟,随机最优潮流由此诞生[2]。随机最优潮流将最优潮流和随机潮流结合在一起,以机会约束的方式联系二者,对随机最优潮流问题进行求解。
随机最优潮流问题中最重要的内容之一是求解最优潮流优化问题,传统的优化方法包括简化梯度法、内点法、解耦法,但是耗时长,收敛性差,对目标函数的要求高,易局部收敛等问题限制了这些算法大范围的应用,因此智能算法被广泛的应用于电力系统的优化问题中,比如遗传算法、粒子群算法、模拟退火法等。
布谷鸟算法(CS:cuckoo search algorithm)也是诸多智能算法之一,具有很强的应用前景,与粒子群算法、遗传算法相比较,布谷鸟算法具有:全局搜索能力强、收敛速度快、所含参数少、通用性和鲁棒性更好等优势[3]。但是存在收敛速度慢,容易陷入局部收敛等问题[4],为解决上述问题,利用量子计算和混沌局部搜索方法改进传统布谷鸟算法,并将其应用于IEEE30节点随机最优潮流问题,并将结果与粒子群算法、经典布谷鸟算法、遗传算法对比,得出改进布谷鸟算法的优越性。
1 基于量子计算和混沌局部搜索的布谷鸟算法
1.1 基本布谷鸟算法介绍
布谷鸟算法是一种新的全局寻优方法,布谷鸟在繁殖期间,采取的是寄生育雏的方式,首先将自己的卵产在寄主鸟的窝,让其孵化自己的卵,如果被发现,自己的卵就会被寄主踢出,这时布谷鸟需要重新寻找寄主,假设被发现的概率为Pa。布谷鸟寻找新寄主采用的是levy飞行机制,是一种随机游走机制,步长满足重尾稳定分布[5]。布谷鸟算法的基本思路为:首先确定空间中每一个鸟窝的适应值,筛选出适应值高的鸟窝,然后利用levy飞行机制更新所有鸟窝的位置,继而判断鸟蛋在该鸟窝中是否会被寄主踢出,方法为:产生一个(0,1)之间均匀分布的随机数Pn,将其与鸟蛋被发现的概率Pa比较,如果Pn大于Pa,说明鸟蛋被发现,于是抛弃该鸟窝,寻找下一个更优的鸟窝。
一般的单目标优化问题可以表述为:
minf(X),s.t.X∈RD
(1)
式中:f为目标函数;X为候选解,设Xi=(xi,1,xi,2,…,xi,n)。则在布谷鸟算法中,X视为一个鸟窝。
Levy飞行机制描述如下:
根据Levy飞行机制,自变量通过下式进行更新:
(2)
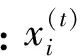
(3)
其中,随机数μ和v服从正态分布;β为在[1,2]之间的常数;Φ的表达式如下所示:
(4)
因此,自变量x可以由下式进行更新:
(5)
布谷鸟算法的求解步骤如下:
(1)初始化。对于每个鸟巢X,都存在n个自变量x,每个x拥有自己的上下限,xmax和xmin。在上下限之间取一个随机值作为每个自变量的初始值,按照这样的方式初始化所有的鸟窝。
(2)初始鸟窝适应值求解。根据适应度函数,求解每一个鸟窝的适应值。
(3)更新鸟窝。利用Levy飞行机制更新每个鸟窝的位置(即自变量的大小),并计算新的鸟窝的适应值,若比原来的高,则替换原来的鸟窝。
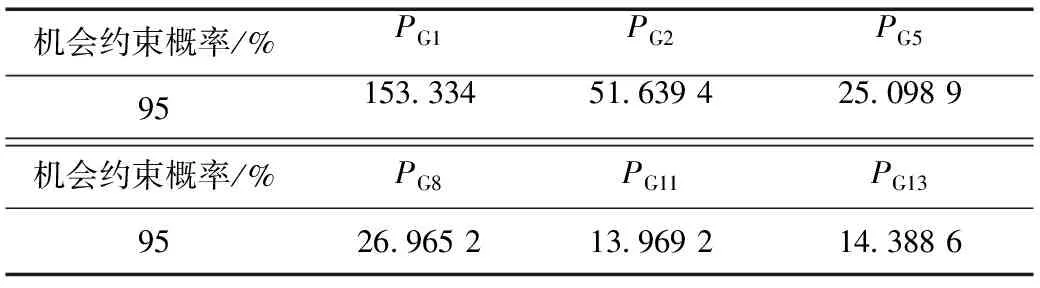
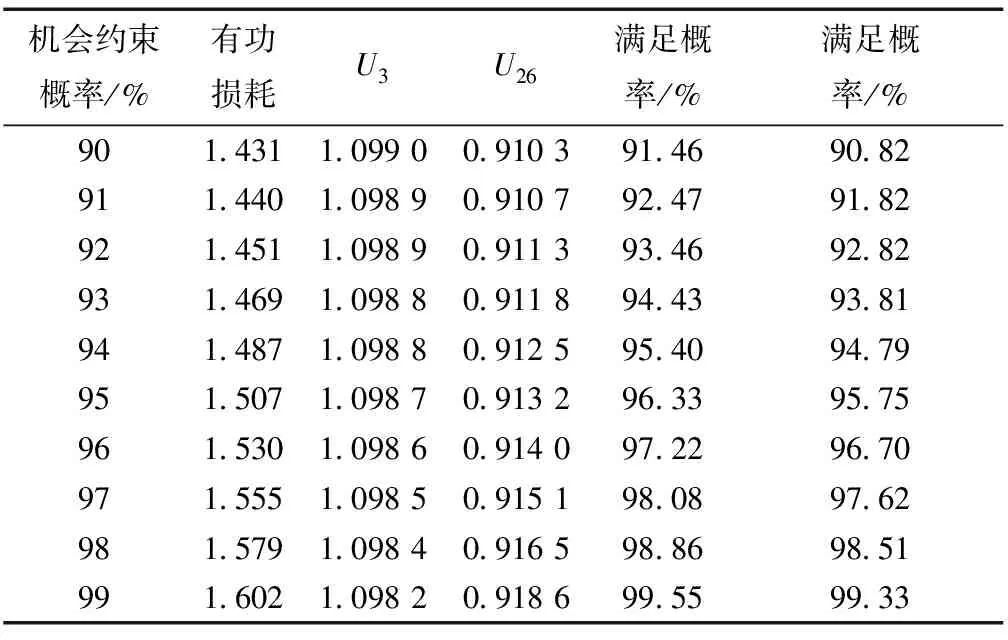
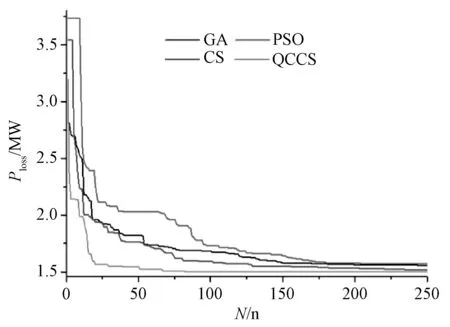
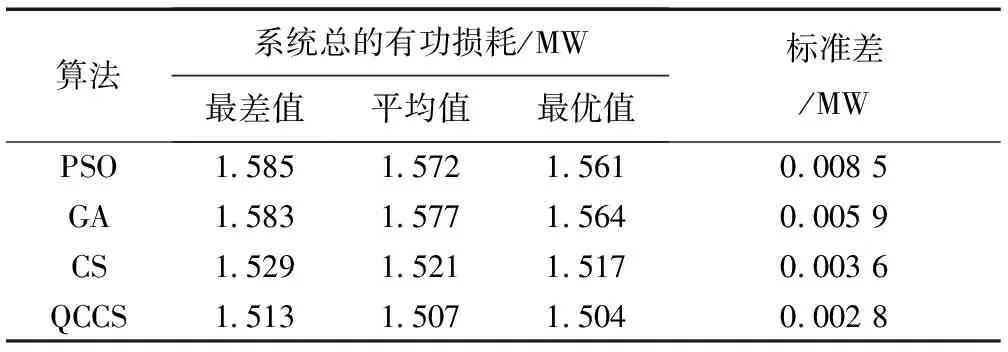
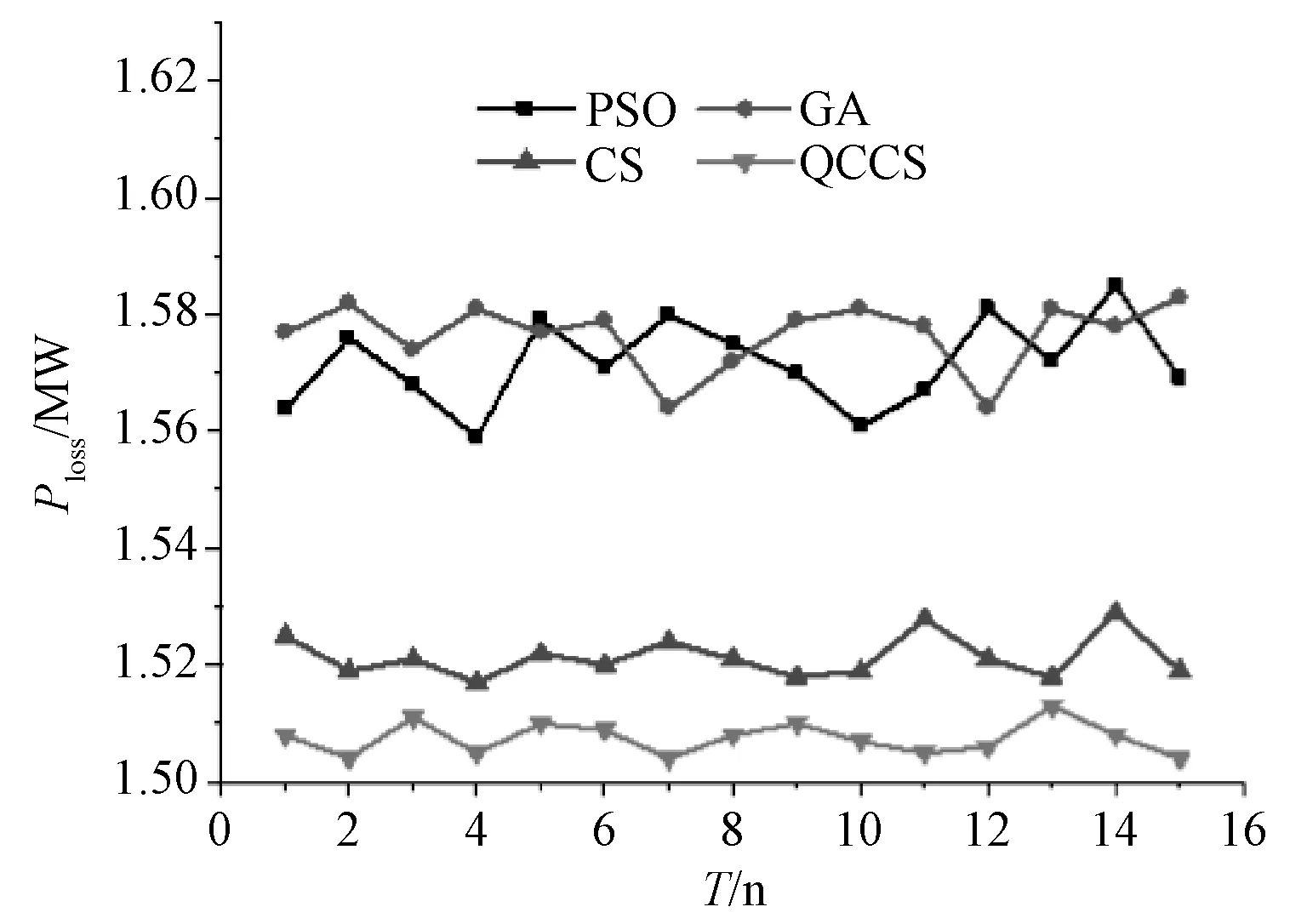
(4)对于新的鸟窝,产生一个[0,1]之间的随机数r,如果r (5)算法结束。如果迭代次数达到设定值,则选择当前鸟窝中最优的那个,作为目标函数的最优解,结束布谷鸟算法。 1.2 量子计算原理 为了解决传统布谷鸟算法收敛速度慢,种群多样性低的问题,本文将量子计算和传统布谷鸟算法结合,提出一种基于量子计算的布谷鸟算法。 量子比特位连接在一起形成量子比特位串,形式为 (6) 也可以表示为: (7) 其中,n为比特位数。如果用量子比特位来表示鸟窝,假设一个鸟窝是m维的,即有m个自变量,每个自变量用n位的量子比特来表示,那么可以用一个m×n位的量子比特来表示该鸟巢。 (8) 量子旋转门:量子比特位在量子旋转门的作用下实现量子进化,与随机变化不同,量子旋转能够实现朝着最优方向变化。量子进化可以表示为: (9) (10) 因此,变化后新的量子比特位为: (11) 1.3 混沌局部搜索 混沌局部搜索是在优化算法第k次迭代产生的种群中,选择适应度最高的个体,记为Zmax,在Zmax附近利用k次混沌局部搜索,产生新的k个个体,选择这k个个体和Zmax中适应度最高的作为该种群的最优个体。混沌局部搜索有助于算法跳出局部收敛,使解更接近最优。 本文在最优个体附近采用混沌序列生成新的个体,混沌序列采取切比雪夫映射: (12) 其中,α为调节系数,可任意设定。 局部混沌搜索步骤: (1)设定常数NC用于计算收缩系数。 (2)在布谷鸟算法第i次迭代时,寻找当前最优鸟窝,记为Xbest。 (3)给定(0,1)内的随机数Z1,根据式(12)产生和鸟窝维度一致的量子比特位Z,编码,二进制转十进制,形成新的鸟窝Xnew。 (13) (14) (4)新鸟窝的修正。根据式(13)计算收缩系数,对新的鸟窝进行修正。 (5)判断局部混沌搜索次数是否达到最大值k,否,返回第(2)步;是,比较k个新个体Xnew和Xbest的适应度,选择最优作为新的Xbest。 1.4 修正的布谷鸟算法步骤 (1)确定鸟窝的维度和每一维的比特数,用量子比特位表示鸟窝。 (2)初始化。用rand的方法,在(0,2π)内产生量子角θi的初始值,并将比特位的二进制编码转化为十进制,即为初始鸟窝的值。 (3)初始鸟窝适应值求解。根据适应度函数,求解每一个鸟窝的适应值。 (4)更新鸟窝。利用Levy飞行机制即式(15)更新每个量子角θi,通过量子角和实际值之间的关系确定新的鸟窝,计算其适应值,并与更新前的鸟窝对比,若适应值高,则替代更新前的鸟窝,反之,则保留更新前的鸟窝。 (15) (5)对于新的鸟窝,产生一个[0,1]之间的随机数r,如果r (6)选择并记录最优鸟窝。利用混沌局部搜索,更新最优鸟窝。以最优鸟窝为目标,生成每个量子比特位的量子旋转角Δθi,利用量子旋转门更新除最优鸟窝以外的其余鸟窝。 (7)判断是否达到迭代次数,若是,则返回最优的鸟窝,否则继续迭代。 2.1 最优潮流模型 与一般的最优潮流不同,随机最优潮流需要考虑系统电源和负荷的随机性,本文的随机最优潮流考虑负荷和分布式电源(光伏)的随机性,认为负荷服从正态分布[6],光伏服从Beta分布[7]。系统不等式约束考虑了发电机有功、无功,发电机电压幅值,节点电压,支路功率和电流。以系统网损最小为目标,建立目标函数如下所示: (16) 式中:Ploss为系统网损;gij为支路电导;Vi,Vj为首末节点电压幅值;δi,δj为首末节点电压相角;NB为节点数。 约束条件如下所示: (1)等式约束 (17) (18) 式(17)和式(18)为系统的功率平衡约束。 (2)不等式约束 (19) (20) (21) (22) (23) (24) 式中:PGi和QGi分别是发电机的有功和无功;VGi和Vi分别是发电机节点的电压和负荷节点的电压;Sij和Iij分别是支路功率和电流。各量在求解过程中必须满足维持在上下限之内。 (3)机会约束 将上述约束转化为机会约束的形式,即变量不要求完全满足约束条件,而是以一定概率满足约束条件,对应的机会约束表达式如下所示: (25) (26) (27) (28) 2.2 随机潮流模型 目前随机潮流的计算方法层出不穷[8-10],但是由于考虑了机会约束,需要得出状态变量的越限概率,为满足上述需求,本文采取了蒙特卡洛模拟法作为随机潮流的计算方法。 基于蒙特卡洛思想的随机潮流过程可以描述为: (1)建立系统随机变量的概率模型; (2)设定抽样次数m,根据概率模型抽样出一系列随机数; (3)将这些随机数分别代入确定性潮流计算中,进行m次潮流计算,得出结果。 2.3 机会约束处理 机会约束处理一般采取改变约束上下限的方式。对于本文的随机最优潮流,当受控变量不满足置信度时,缩小该量约束的上下限,重新进行最优潮流,产生在更小的约束范围内的结果,使后续的随机潮流得出的受控变量能够更大程度地满足置信度。 稳态系统的节点电压一般不会同时越上下限很多,其他受控变量也如此,因此,越限情况可由下式之一表述: (29) (30) 当出现式(29)的情况,用式(31)修改上下限。 (31) 当出现式(30)的情况,用式(32)修改上下限。 (32) 式中:xmin2、xmax2为更新后的受控变量x的上下限。 随机最优潮流步骤分为确定性最优潮流、随机潮流和根据随机潮流结果是否满足机会约束来修正确定性最优潮流约束条件3步。 其中,确定性最优潮流以IEEE30节点中PV节点的输出功率为自变量,作为布谷鸟算法的鸟窝,以2.1节中目标函数的倒数作为适应度函数,利用布谷鸟算法对该优化问题进行求解。随机潮流利用2.2节中的模型进行求解。约束的修正利用2.3节中机会约束处理的方法。 图1为基于优化布谷鸟算法的随机最优潮流问题求解流程。 图1 基于优化布谷鸟算法的随机最优潮流问题求解流程 (1)假定系统随机变量为定值,设为均值,用布谷鸟算法求解系统确定性最优潮流,得到一组优化方案。 (2)考虑随机变量的随机性,利用蒙特卡洛模拟法,求解该组优化方案下系统的随机潮流。 (3)从得出的受控变量(节点电压、发电机无功、支路功率、支路电流)随机数据中,判断是否满足机会约束,若满足,这组优化方案即为最终方案,结束计算;反之,进行第(4)步。 (4)判断是否达到最大迭代次数,是则停止计算;否则,对于违背机会约束的受控变量,利用式(31)和式(32)调整约束范围,返回第(1)步重新进行确定性最优潮流。 IEEE 30节点系统中包含6台发电机、4台变压器、2台无功补偿装置,系统拓扑结构和相关数据见文献[11]。各个节点电压的范围在0.9~1.1 p.u.之间,变压器的变比范围在0.95~1.05 p.u.之间,步长为0.01 p.u.,无功补偿装置的取值范围在0~0.4 p.u.之间,步长为0.01 p.u.。机会约束的概率p全部取95%,随机最优潮流结果见表1。 表1 p=95%时随机最优潮流结果 从表2中可以看出,随着机会约束概率的增大,系统有功损耗随之增大,体现了机会约束对最优潮流的约束作用。当机会约束概率为95%时,有功损耗比传统确定性潮流高了2.86%,是由于系统加入了随机变量,导致不得不缩小约束范围。从IEEE30系统中,选取靠近发电机的节点3和远离发电机的节点26,观察不同机会约束概率下它们的随机分布情况,可以看出计算结果趋于保守。 表2 不同约束概率下的计算结果 为了验证本文改进的布谷鸟算法优越性,本文比较了粒子群算法(PSO)、遗传算法(GA)、经典布谷鸟算法(CS)、基于量子计算和局部混沌搜索的布谷鸟算法(QCCS)4种方法,对比上述算例的计算速度情况。图2显示了4种算法的收敛速度,横坐标N为种群代数,纵坐标Ploss为系统功率损耗。 图2 IEEE30节点4种优化算法收敛对比图 从图2中可以看出: (1)QCCS算法收敛速度明显快于其他算法,基本在25代之前就收敛结束,而CS、GA和PSO则分别在80、120和160代之后才能够趋于稳定。 (2)趋于稳定时,收敛值从高到低的算法排序为PSO、GA、CS和QCCS,说明QCCS不仅收敛速度最优,而且收敛值也最优。 表3显示了各优化算法计算同一算例15次,结果的分布情况,包括最差值、平均值、最优值和标准差。 表3 4种算法总有功损耗对比 从表中可以看出: (1)QCCS的最差值最小,是由于每一次混沌局部搜索后,都使用量子旋转门更新种群中除最优以外的其余个体,导致所有个体都向最优个体靠近,体现了QCCS在收敛性方面的优势。 (2)QCCS的最优值最小,是由于得出每一代种群后,都会利用混沌局部搜索方法,更新最优个体,体现了QCCS的收敛速度和收敛值的优化。 (3)QCCS的平均值最小,说明了优化结果最佳。 (4)QCCS的标准差最小,体现了算法的稳定性。 图3为详细的4种方法15次运行的结果。横坐标T为运行次数,图中可以直观看出CS和QCCS的结果和稳定性都优于PSO和GA,而且与CS相比,QCCS具有一定的优化效果。 图3 IEEE 30节点15次运行的有功损耗结果 为解决传统布谷鸟算法收敛速度慢,易陷入局部解的问题,本文将量子计算理论和混沌局部搜索与传统布谷鸟算法结合,提出一种新的布谷鸟算法。并将其应用于随机最优潮流,分析比较其与粒子群算法、遗传算法、经典布谷鸟算法的计算结果。结果表明,修正后的布谷鸟算法收敛性和稳定性有所提升。 本文随机最优潮流采用的是机会约束的方式,将约束条件以机会约束的形式表现,随机潮流得出的越限变量通过修正上下限来更新最优潮流结果,使随机潮流和最优潮流很好地结合在一起,算例采用IEEE30节点,得出了不同的约束概率下的计算结果。 [1]李振杰, 袁越. 智能微网——未来智能配电网新的组织形式[J]. 电力系统自动化, 2009, 33(17): 42-48. [2]孙国强, 李逸驰, 向育鹏, 等. 计及风速时空相关性的含风电场电力系统动态随机最优潮流计算[J]. 中国电机工程学报, 2015, 35(17): 4308-4317. [3]张永韡, 汪镭, 吴启迪. 动态适应布谷鸟搜索算法[J]. 控制与决策, 2014, 29(4): 617-622. [4]翁振星, 石立宝, 徐政, 等. 计及风电成本的电力系统动态经济调度[J]. 中国电机工程学报, 2014, 34(4): 514-523. [5]冯登科, 阮奇, 杜利敏. 二进制布谷鸟搜索算法[J]. 计算机应用, 2013, 33(6): 1566-1570. [6]张新松, 顾菊平, 郭晓丽. 基于离散概率潮流的大风电接入后的电网规划[J]. 中国电力, 2014, 47(4): 128-133. [7]殷桂梁, 张雪, 操丹丹, 等. 考虑风电和光伏发电影响的电力系统最优旋转备用容量确定[J]. 电网技术, 2015, 39(12): 3497-3504. [8]徐青山,黄煜,刘建坤,等. 采用混合高斯模型及边缘变换技术的蒙特卡洛随机潮流方法[J]. 电力系统自动化, 2016, 40(16):23-30. [9]代景龙, 韦化, 鲍海波, 等. 基于无迹变换含分布式电源系统的随机潮流[J]. 电力自动化设备, 2016, 36(3): 86-93. [10]刘小团, 赵晋泉, 罗卫华, 等. 基于TPNT和半不变量法的考虑输入量相关性概率潮流算法[J]. 电力系统保护与控制, 2013, 41(22): 13-18. [11]蒋凌, 潘志, 成天乐. 含风电电力系统旋转备用的鲁棒优化方法研究[J]. 电力科学与工程, 2013, 29(4): 1-6. Stochastic Optimal Power Flow Based on Modified Cuckoo Search Algorithm ZHOU Qian1,WEI Peng1, LIU Chaojun2 (1. Jiangsu Electric Power Test Research Institute, Nanjing 211103, China;2. State Grid Chongqing Electric Power Company, Chongqing 402260, China) A chance-constrained programming model is established for stochastic optimal power flow considering of the randomness of loads and DGs. In this model, a modified cuckoo search algorithm is used to find the optimal solution. The algorithm is a combination of the cuckoo search algorithm, quantum computation and chaotic local search. The Chebyshev mapping is adopted to produce a chaotic sequence, and quantum rotating gate is used for better convergence. Using the stochastic power flow optimization problem as an application scenario and considering of the randomness of the distributed power as well as the load, a chance constrained model is then put forward in this paper. And the chance constraint is treated by modifying the upper and lower bounds of the variables. Taking IEEE33 node as an instance, four different intelligent algorithms are applied and calculation results and convergence performance are obtained. The results show that the modified cuckoo search algorithm can recognize local solution and has excellent convergence performance. quantum computation; chaotic local search; cuckoo search algorithm; stochastic optimal power flow; chance-constrained programming 10.3969/j.ISSN.1672-0792.2017.02.003 2016-10-05。 国家自然科学基金(51577028)。国家电网公司科技项目“新能源发电预测误差对电网安全运行影响评价方法研究”。 TM711 A 1672-0792(2017)02-0014-07 周前(1978-),男,高级工程师,主要从事电力系统运行分析和规划研究。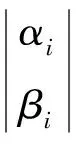
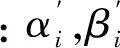
2 随机最优潮流模型
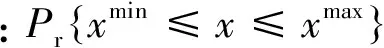
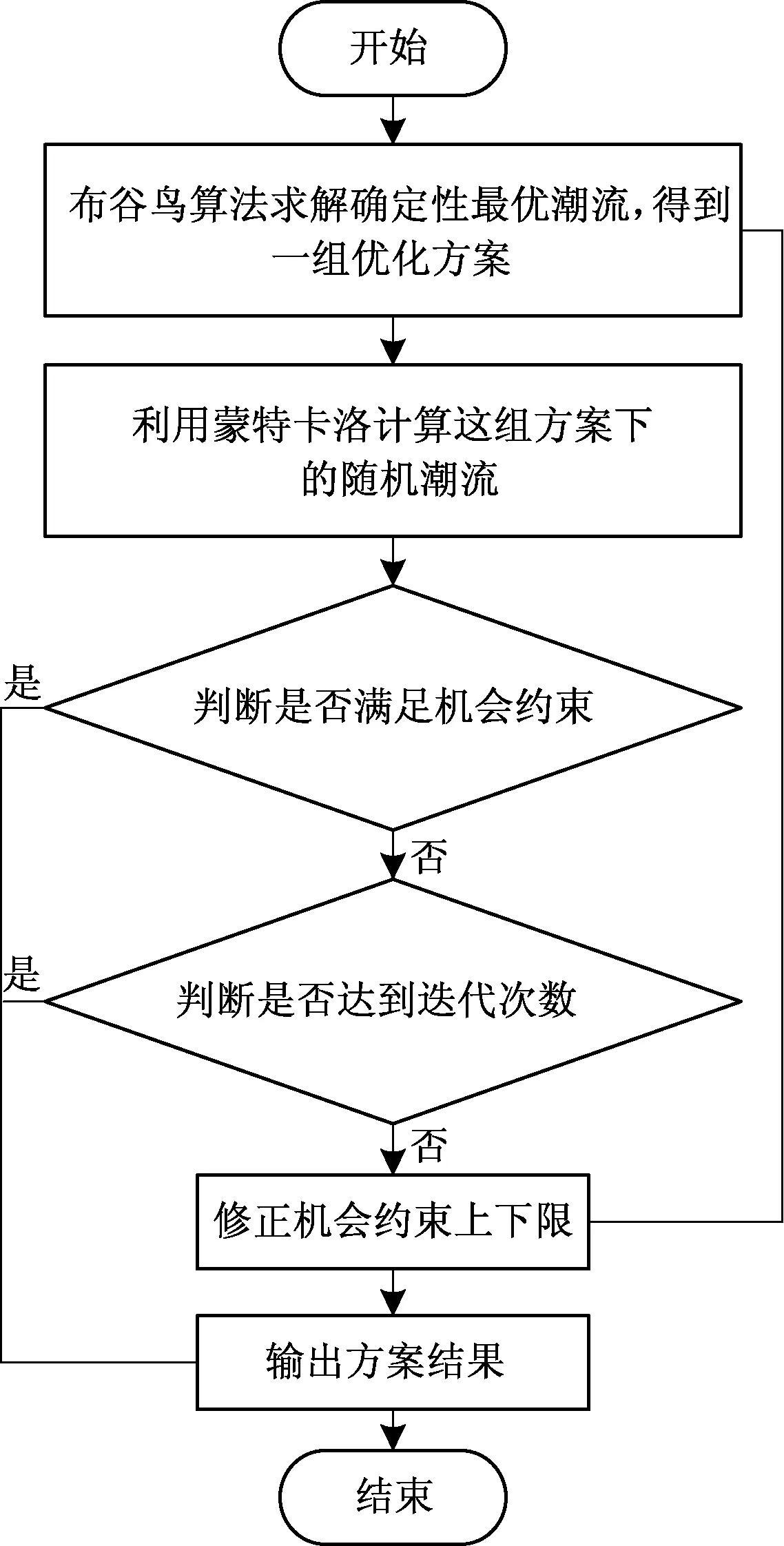
3 基于优化布谷鸟算法的随机最优潮流问题求解流程
4 算例分析
5 结论

