Deformation and failure analysis of river levee induced by coal mining and its influence factor
Meng Li , Jixiong Zhang, Nan Zhou, Qiang Zhang
1 Introduction
Currently, significant coal resources in China are buried beneath river levees. Therefore,the exploration of such coal resources is supposed to affect the normal use of river levees.When coal is mined, the equilibrium stress in those rocks around the coal resources is lost so as to result in the movement and fracture of overlying strata [Booth (1986); Qian, Xu and Shi (2003)]. Finally, the ground surface is damaged and subsides, which then causes the deformation and failure of river levees. At present, there is a paucity of research into the influence of mining on the stability of river levees. Wang et al. [Wang, Lian and Chen(2013)] studied the movement and deformation of river levees under the influence of mining by simulating surface ground movement during coal mining under river levees.By using a FLAC3D, Li et al. [Li, Hu, Chen and Yang (2008)] simulated the movement and deformation of the river levee of Nantuo River influenced by the mining of the 6123 working face in Baishan Mine (Anhui, China). Wang Lieping et al. [Wang, Hu, Chen,Chen and Li (2009)] predicted the mining subsidence of the southern river levee of Nantuo River lying on thick, unconsolidated, overburden using a probability integral method and FLAC3Dsoftware. Wu et al. [Wu, Wang, Yin, Sun, Jia and Li (2007)]investigated the influence of mining subsidence on the safety of dams by combining numerical calculations and field measurement. All these research projects focus on the deformation of river levees induced by mining. However, since many factors can influence the stability of river levees, a method to evaluate the stability of river levees induced by mining as well as the criterion to determine whether river levees are damaged or not is required. Therefore, based on the deformation characteristics of river levees under mining conditions, this research established a mechanical model for the deformation of river levees and proposed a failure criterion for river levees. After calculating the deformation and stress distribution in typical river levees, this work further analysed those factors which could influence the stability of river levees. This aimed to provide a theoretical basis for the prediction of the deformation and failure of river levees induced by mining.
2 Deformation characteristics of river levees induced by mining
Before the mining of underground coal, the underground stress state is in equilibrium.When the coal is mined out, the stress in the surrounding rocks is redistributed, resulting in the movement and fracture of overlying strata [Mohammad, Mohammad, and Abbas(2015); Cao, Zhou, Xu and Li (2014)]. Finally, these cracks develop, from the bottom up,to the ground surface, causing surface subsidence [Can, Kuscu, and Kartal (2012); Wang,Zhang, Guo, and Zha (2014)]. As a result, river levees in the range of surface subsidence are affected. This comes from their foundation and causes their deformation. When the deformation exceeds the capacity of a river levee to sustain it, damage ensues. The horizontal deformation of the surface is mainly attributed to the failure of river levees as their lateral tensile stiffness is small and they are easily cracked, which finally results in their failure. Figure 1 shows the mining-induced deformation characteristics of river levees.

Figure 1: Mining-induced deformation characteristics of river levees
3 Mechanical analysis of deformation and failure of river levees
3.1 Mechanical model
As surface subsidence basins enlarge and deepen with the advance of a working face,river levees at different positions on the subsidence basin are subject to different influences. Meanwhile, the deformation and stress at different positions of a river levee are different. Therefore, two coordinate [Tan and Deng (2004)] systems describing the surface subsidence and river levee subsidence, which are independent and interconnected,can be constituted to study the deformation and stress distribution of river levees under the influence of mining (Figure 2).
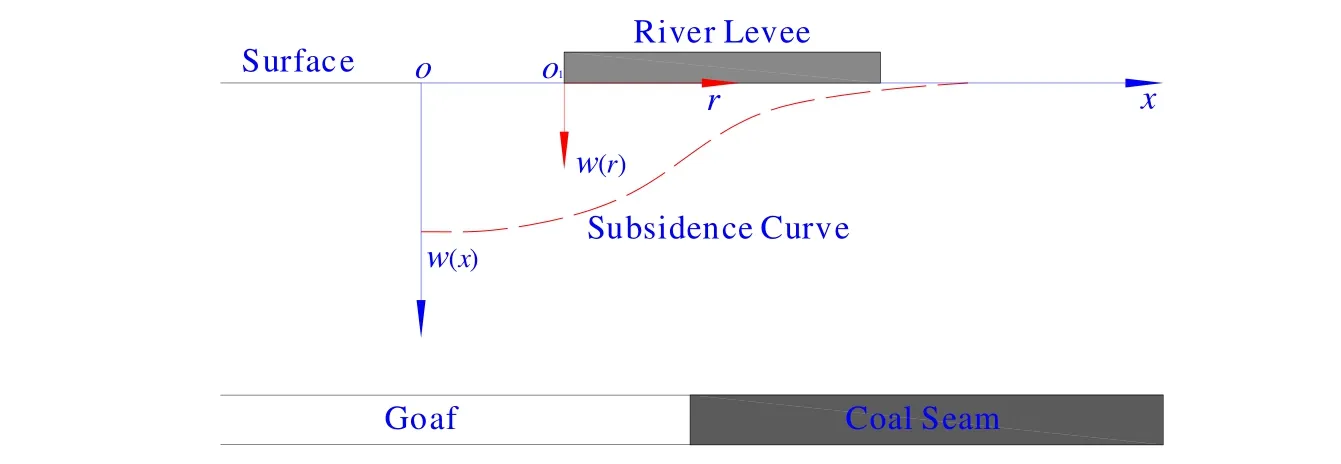
Figure 2: Coordinate systems for the river levee and the surface subsidence
Taking the maximum surface subsidence point o as the origin, a coordinate system (w(x)-o-x) for surface subsidence is established with the advancing direction of the working face as the x-axis which lies horizontally to the right, and the vertical, w(x)-axis which extends vertically downwards, represents the surface subsidence at point x. While by regarding the left-hand end o1 of the river levee, at x, to the maximum surface subsidence point o as the origin, a coordinate system (w(r)-o1-r) for river levee subsidence was established. Thereinto, abscissa r is consistent with the direction of the x-axis and the subsidence of any point r in the river levee is recorded as w(r). The corresponding values of surface subsidence are represented as w(x+r).
Since the deformation of river levees induced by mining is similar to that seen in beam bending problems, the river levee could be regarded as a beam on an elastic foundation.Based on Winkler foundation theory, the foundation subsidence is positively related to the foundation force.

Where, σ(r) is the subgrade reaction at any point on the foundation at the bottom of the river levee, while k represents the elastic foundation coefficient.
According to the theory of coal mining subsidence, a trigonometric function [Zou, Deng,and Ma (2003); Tan, and Deng (2007)] is applied to describe the surface subsidence curve:

Where, L is the half-basin length (the distance between the point of maximum subsidence and the boundary of the subsidence basin) and wmaxis the maximum value of surface subsidence.
3.2 Solutions to the mechanical model
The load on the river levee is the difference between its self-weight and the foundation force.

Where, q is the self-weight of the river levee.
Based on Winkler theory of foundation beams, the differential equation describing the flexure of a river levee on an elastic foundation is:

Where, E is the elastic modulus of the soil comprising river levee, and I is the moment of inertia of the cross-section of the river levee normal to the axis of bending.
By substituting Formula (2) into Formula (4), the differential equation governing flexure of the river levee can be rewritten as follows:
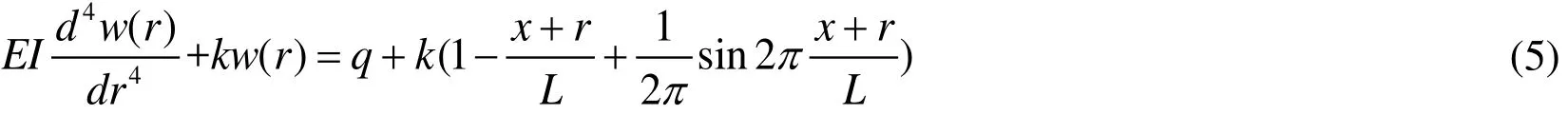
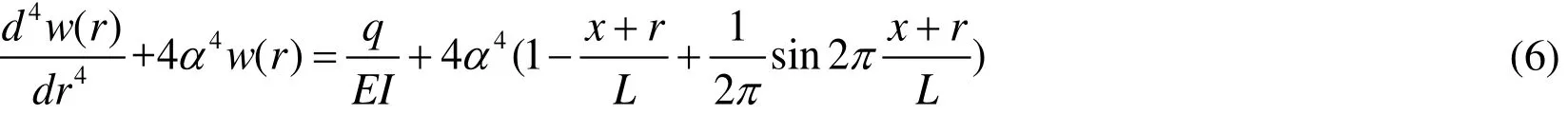
The solutions of the homogeneous differential equation (6) are composed of general and special solutions. By processing (6), the following subsidence formula for the river levee can be obtained:

Where, d1to d4are coefficients to be solved as determined by the boundary conditions.
Since the river levee is supposed to move with the subsidence of the surface, the two ends of the river levee can regarded as free. Then, the specific boundary conditions are acquired as follows:

Where, l is the length of the river levee.
By substituting the relevant parameters into (7), and combining this with the boundary conditions (8) for the river levee, the undetermined coefficients d1to d4can be found.
After subtracting the subsidence caused by the self-weight of the river levee, the subsidence thereof induced by mining can be acquired.
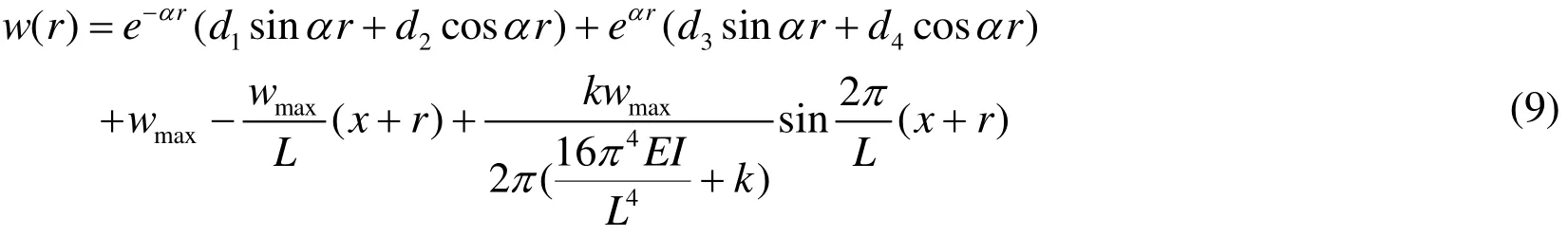
The corresponding surface subsidence is
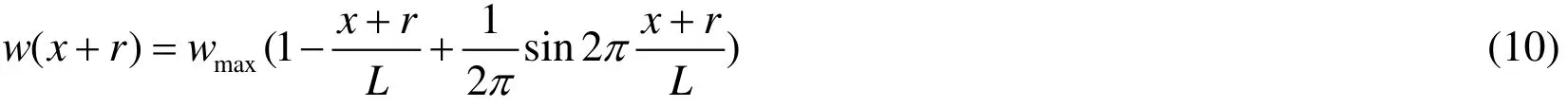
3.3 Failure criterion for a river levee
The stress in the river levee under the influence of mining is:

The bending moment in the river levee during mining is:
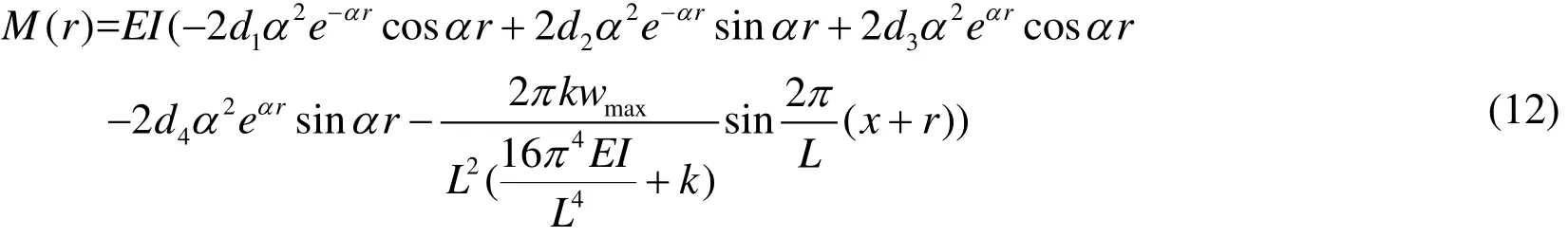
Horizontal tensile deformation is the main factor damaging the river levee, therefore the first strength theory is used to determine the failure of the river levee. Under the influence of mining, the maximum tensile stress in the river levee occurs at the bottom of the river levee, that is:

Where, Izis the moment of inertia of the section about the neutral axis of the beam, while b and h are the width and height of the river levee.
When the maximum tensile stress at the bottom of the river levee is larger than the tensile strength, the river levee is supposed to be damaged and:

Where, σtis the tensile strength of the river levee.
4 Analysis of examples
4.1 Calculation parameters
The deformation and failure of a river levee under the influence of mining was studied based on actual cases: the river levee was just under the 14120 working face and parallel to the advancing direction of the working face (Figure 3). According to the subsidence of the adjacent working face in this region after mining, the maximum surface subsidence wmaxof the river levee and the half-length L of the surface subsidence basin were set to 0.8 m and 300 m, respectively. In addition, the width b, height h, and length l of the river levee were 5 m, 8 m, and 120 m, separately. In addition, with the elastic modulus E and self-weight load q being 2.5 GPa and 0.16 MPa, the tensile strength σtof the river levee was 0.8 MPa. Moreover, the distance x between the river levee to the point of maximum subsidence was 30 m and the foundation coefficient k was 45 MN/m3.
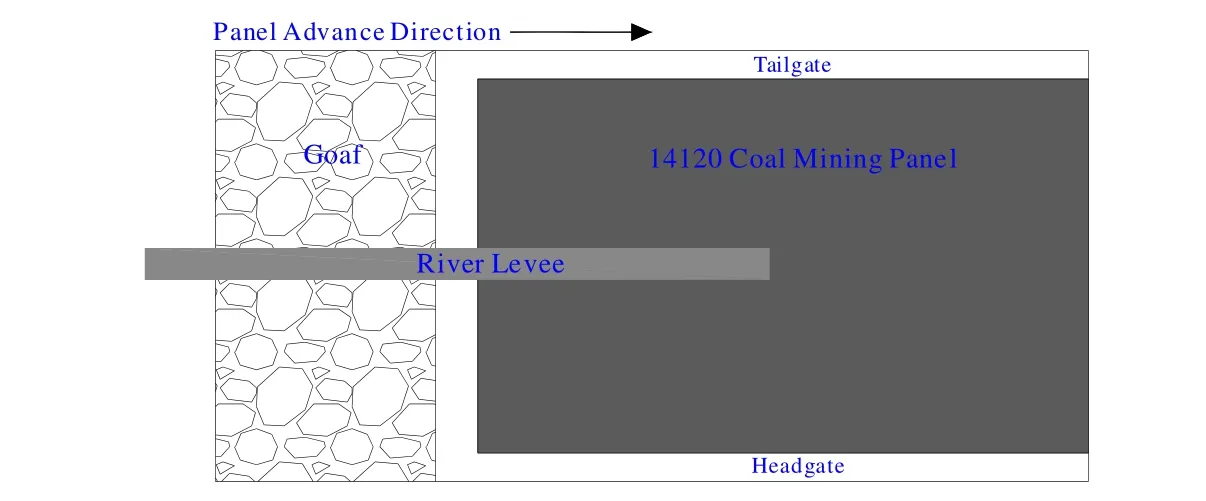
Figure 3: Positions of the river levee and the 14120 working face
4.2 Deformation and failure of river levees
Based on the boundary conditions in (8), d1to d4are obtained as follows by substituting the above parameters into (7):

The mining-induced subsidence of the river levee is acquired by substituting d1to d4into(9):
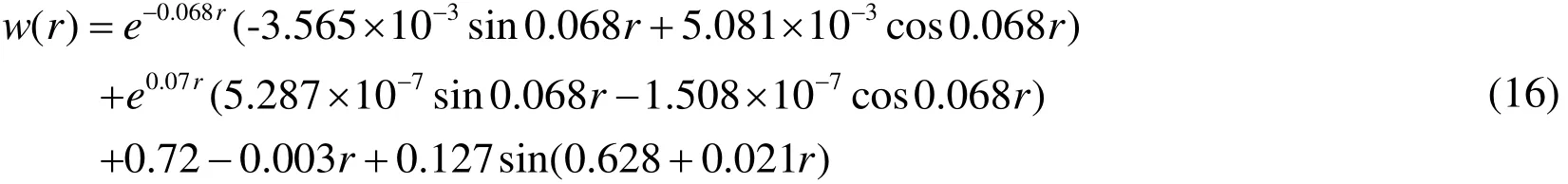
According to (16), the subsidence at different positions along the river levee is as shown in Figure 4.
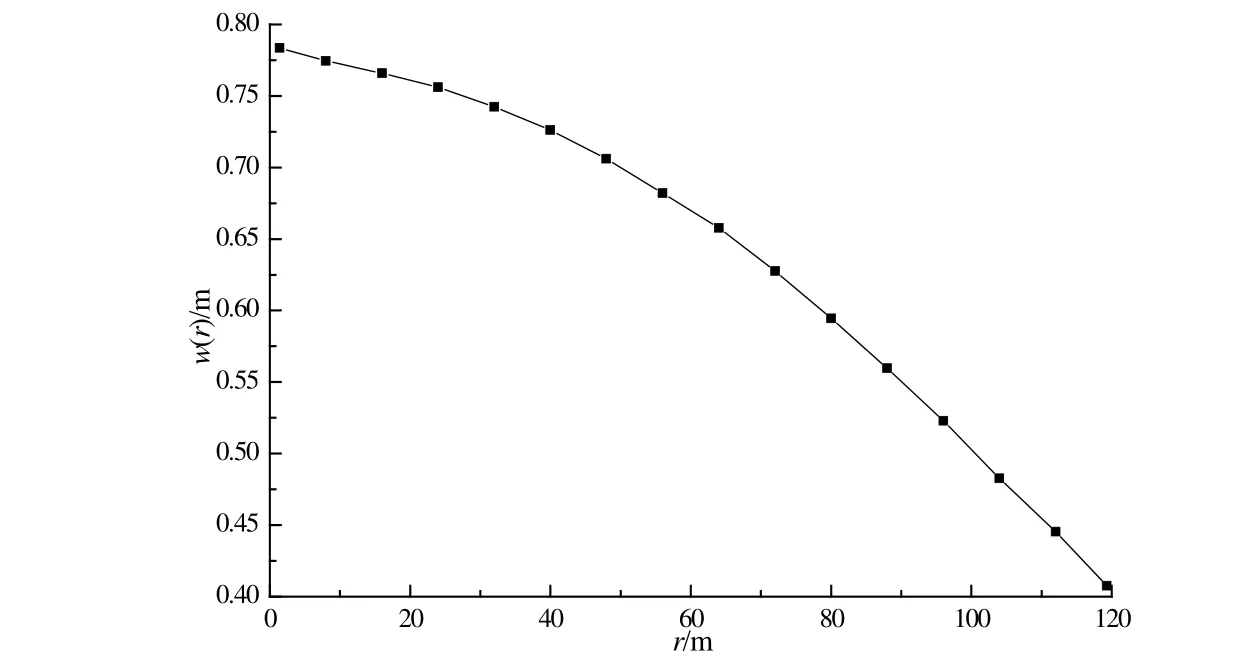
Figure 4: The subsidence of different positions along the river levee
Based on Figure 4, it can be seen that when the river levee is not influenced by mining,the maximum subsidence thereof is 0.78 m, which is found at the left-hand end of the river levee. Moving right along the river levee, the subsidence decreases continuously until reaching the minimum value of 0.41 m which is found at the right-hand end of the river levee. Furthermore, the tensile stress at the bottom of the river levee is given by (13)as:
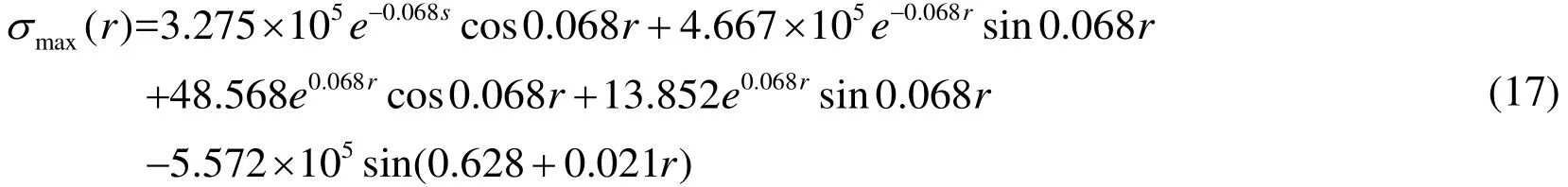
Based on (17), the tensile stress at different positions at the bottom of the river levee is as shown in Figure 5.

Figure 5: Tensile stress at different positions at the bottom of the river levee
As seen in Figure 5, the maximum horizontal stresses on the river levee at different positions are distributed in an arcuate manner. When the river levee is not influenced by mining, the maximum tensile stress at the bottom of the river levee is 0.58 MPa which is observed at a point 47 m from the left-hand end thereof. As the maximum tensile stress is less than the tensile strength of the river levee, therefore, according to the failure criterion in (14), the river levee is not damaged.
4.3 Analysis of the factors affecting levee subsidence
There are, in the main, three factors including the maximum surface subsidence, the halflength of the surface subsidence basin, and the foundation coefficient which can affect the deformation and failure of the river levee. Therefore, the influence of these factors on the stability of the river levee is analysed as follows.
(1) The maximum surface subsidence
Figure 6 shows the influence of the maximum surface subsidence on the stability of the river levee.
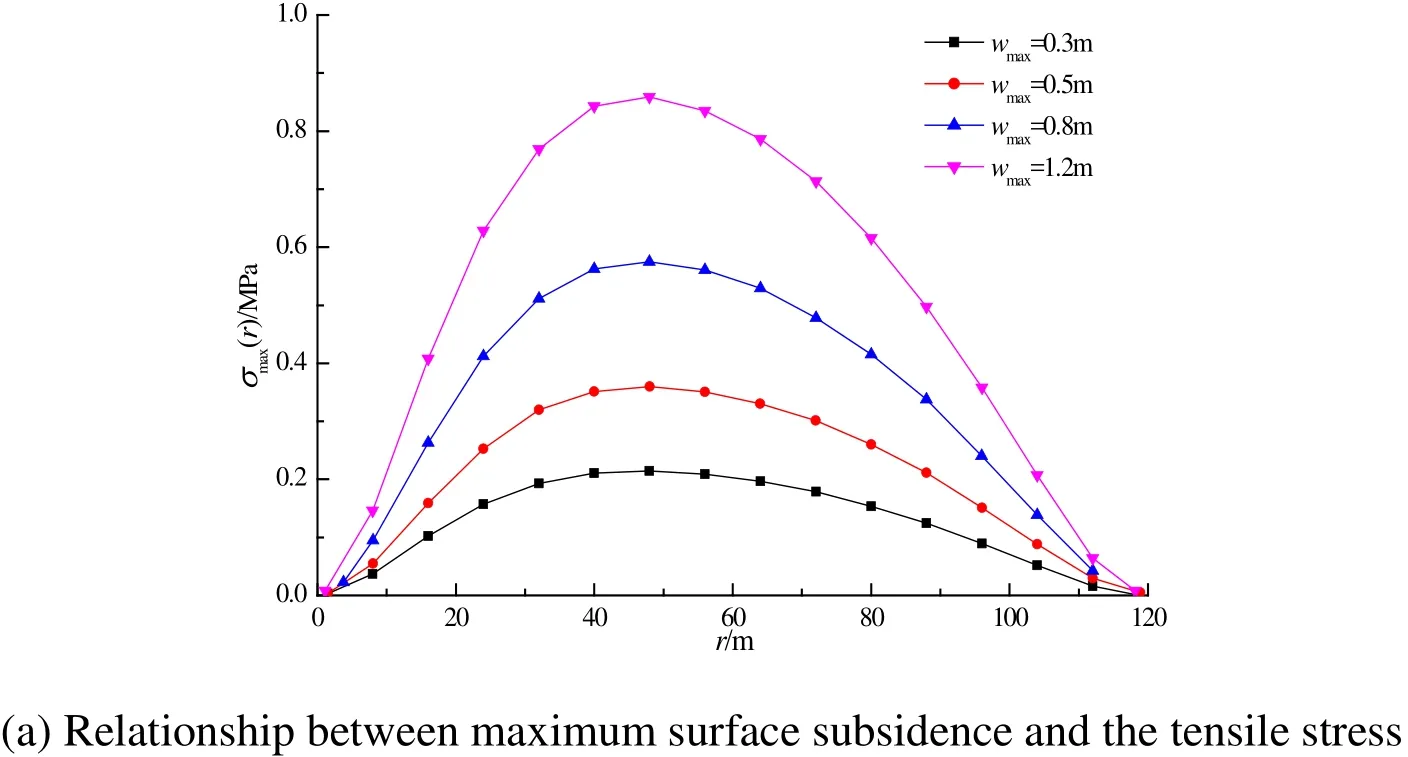
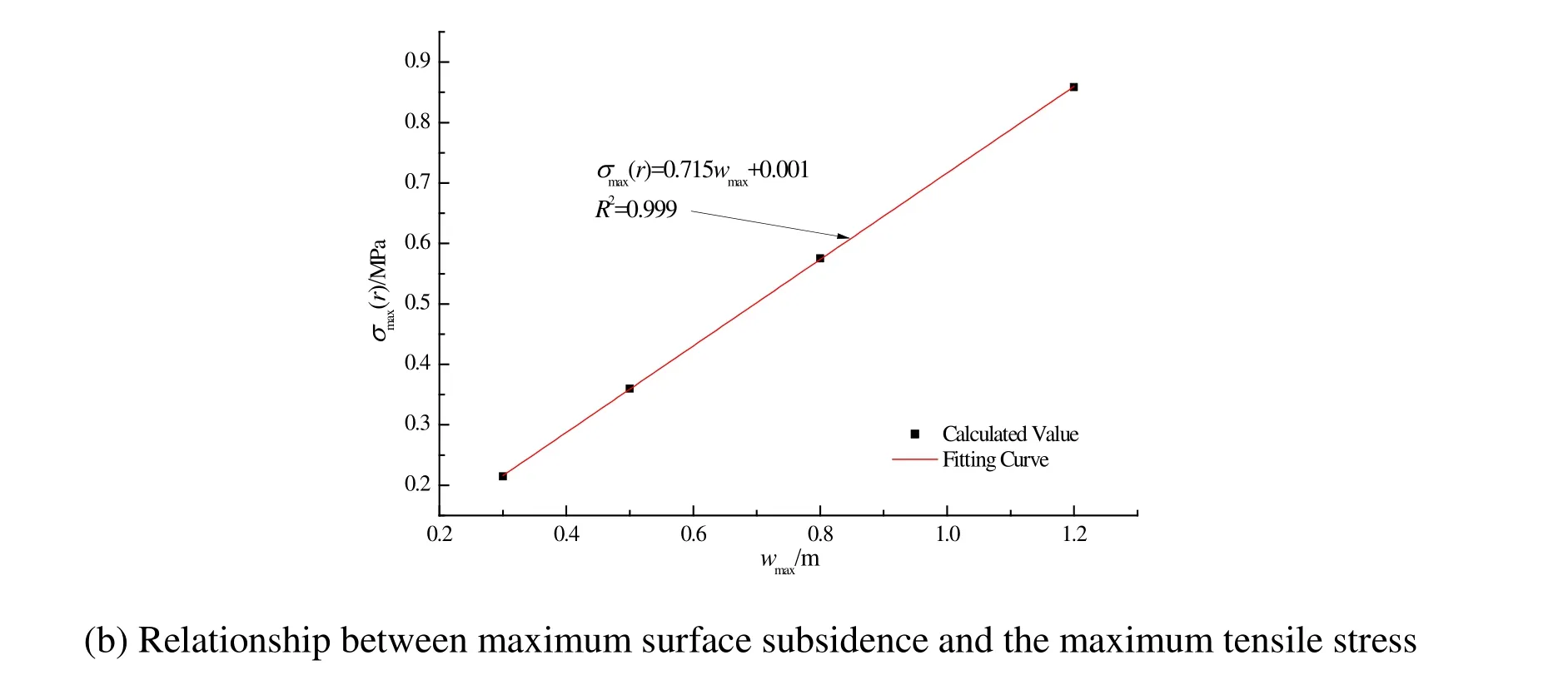
Figure 6: Influence of the maximum surface subsidence on the river levee
From Figure 6, it is seen that the maximum surface subsidence significantly influences the river levee: upon the gradual increase in maximum surface subsidence, the tensile stress at the bottom of the river levee continuously increases. The maximum surface subsidence of, and the maximum tensile stress on, the river levee are linearly related:when the maximum surface subsidence increases from 0.3 m to 1.2 m, the maximum tensile stress correspondingly increases from 0.215 MPa to 0.859 MPa. When the maximum surface subsidence reached 1.2 m, the river levee was damaged. Thus it can be seen that, reducing the height of the working face was beneficial in that it decreased the influence of mining on the river levee.
(2) The half-length of the surface subsidence basin
The influence of the half-length of the surface subsidence basin on the stability of the river levee is shown in Figure 7.
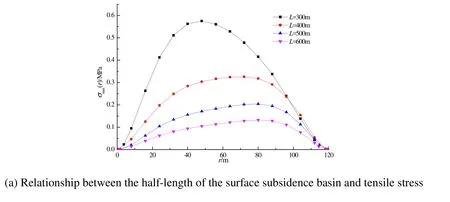

Figure 7: Influence of the half-length of the surface subsidence basin on the river levee
As shown in Figure 7, the half-length of the surface subsidence basin exerts a significant influence on the river levee: the tensile stress decreases with increasing half-length of the surface subsidence basin, but by decreasing amounts. The half-length of the surface subsidence basin and the maximum tensile stress on the river levee are fitted by a polynomial relationship: when the half-length of the surface subsidence basin increased from 300 m to 600 m, the maximum tensile stress decreased from 0.575 MPa to 0.132 MPa. Therefore, it can be seen that increasing the advancing length of the working face can decrease the influence of mining on the river levee.
(3) The foundation coefficient


Figure 8: Influence of the foundation coefficient on the river levee
Figure 8 shows the influence of the foundation coefficient on the stability of the river levee.By analysing Figure 8, it can be seen that the foundation coefficient exerts no obvious influence on the stability of the river levee. The tensile stress increases with increasing foundation coefficient. However, the amplitude of this increase gradually diminished.The foundation coefficient and the maximum tensile stress on the river levee had a polynomial relationship: when the foundation coefficient increased from 15 MN/m3to 100 MN/m3, the maximum tensile stress increased by only 0.021 MPa. Thus it can be seen that softening of the foundation was beneficial with regard to decreasing the influence of mining on the river levee.
5 Conclusions
(1) The lateral deformation of the ground surface (under tension) is the major factor leading to failure of such river levees. Since the river levees have poor resistance to lateral (tensile) deformation, cracks readily occur in river levees subject to tensile deformation: this ultimately damages them.
(2) Based on the deformation characteristics of typical river levees under the influence of mining, this research established a mechanical model of the deformation of a levee by using a typical surface subsidence function. Moreover, a failure criterion for the river levee was proposed.
(3) After the analysis of specific examples, the deformation and stress distributions were obtained for typical river levees under the influence of mining. When the maximum tensile stress at the bottom of the river levee was less than its tensile strength, the river levee was undamaged. Moreover, this research further analysed the influence of three key factors including: the maximum surface subsidence, the half-length of the surface subsidence basin, and the foundation coefficient, on the stability of a typical river levee.Results showed that reducing the mining height of the working face and the foundation coefficient, and increasing the advancing length of the working face, were beneficial to a reduction in the influence of mining on the river levee.
Acknowledgement Financial support for this work, provided by Project of Jiangsu Distinguished Professor (2015-29) and Jiangsu Province Fourth 333 Engineering(BRA2015311).
Booth, C. J. (1986): Strata-movement concepts and the hydrogeological impact of underground coal mining. Ground Water, vol. 24, no. 4, pp. 507–515.
Can, E.; Kuscu, S. and Kartal, M. E. (2012): Effects of mining subsidence on masonry buildings in Zonguldak hard coal region in Turkey. Environmental Earth Sciences, vol.66, no. 8, pp. 2503–2518.
Cao, Z. Z.; Zhou, Y. J.; Xu, P.; Li, J. W. (2014): Mechanical response analysis and safety assessment of shallow-buried pipeline under the influence of mining. CMES:Computer Modeling in Engineering & Sciences, vol. 101, no. 5, pp. 351–364.
Li, M.; Hu, K.; Chen, Z. Q.; Yang, R. (2008): Numerical simulation prediction study of surface subsidence caused by coal mining under the bank of Nantuo river. Journal of Anhui University of Science and Technology (Natural Science), vol. 28, no. 2, pp. 6–10.Mohammad, R.; Mohammad, F. H.; Abbas, M. (2015): Determination of longwall mining-induced stress using the strain energy method. Rock Mechanics and Rock Engineering, vol. 48, no. 6, pp. 2421–2433.
Qian, M. G.; Xu, J. L.; Shi, P. W. (2003): Mining Pressure and Ground Control. China University of Mining & Technology Press.
Tan, Z. X.; Deng, K. Z. (2004): Coordinating work model of ground, foundation and structure of building in mining area. Journal of China University of Mining &Technology, vol 33, no. 3, pp. 264-267.
Tan, Z. X.; Deng, K. Z. (2007): Study on change laws of additional ground reaction force of buildings in mining area. Journal of China Coal Society, vol. 32, no. 9, pp. 907–911.
Wu, X.; Wang, X. G.; Yin, Q. W.; Sun, Y. D.; Jia, Z. X.; Li, X. Q. (2007): Study on coal mining in seam under large reservoir areas. Journal of China Coal Society, vol. 32,no. 12, pp. 1273–1276.
Wang, L. P.; Hu, K.; Chen, Y. P.; Chen, Z. Q.; Li, M. (2009): Mining subsidence prediction of Nantuo river bank under condition of thick and unconsolidated overburden.Coal Science & Technology, vol. 37, no. 12, pp. 96–99.
Wang, C. J.; Lian, W. L.; Chen, Y. (2013): Deformation laws of river levees under the influence of mining. Energy Technology & Management, vol. 38, no. 3, pp. 159–162.
Wang, L.; Zhang, X. N.; Guo, G. L.; Zha, J. F. (2014): Research on surface subsidence prediction model of coal mining with solid compacted backfilling. Rock & Soil Mechanics, vol. 35, no. 7, pp. 1973–1978.
Zou, Y. F.; Deng, K. Z.; Ma, W. M. (2003): Mining Subsidence Engineering. China University of Mining & Technology Press.
 Computer Modeling In Engineering&Sciences2017年2期
Computer Modeling In Engineering&Sciences2017年2期
- Computer Modeling In Engineering&Sciences的其它文章
- TRISim: A Triage Simulation System to Exploit and Assess Triage Operations for Hospital Managers- Development, Validation and Experiment -
- Plane Vibrations in a Transversely Isotropic Infinite Hollow Cylinder Under Effect of the Rotation and Magnetic Field
- Uniform Query Framework for Relational and NoSQL Databases
- Devanagari Handwriting Grading System Based on Curvature Features
- Glass Fibre Reinforced Concrete Rebound Optimization
- Local and biglobal linear stability analysisof parallel shear flows
