借助几何直观发展小学生的数学能力
【摘要】在数学教学中,借助几何直观有助于发展小学生的概念表征能力、问题描述能力和分析推理能力,可以深化学生对数学知识本质的认识,提升他们的数学素养。几何直观不仅是适合小学生身心发展的教学策略和思想,更是一种有效的学习方法,需要教师智慧地将其融入教学。
【关键词】几何直观;数学能力;概念表征能力;问题描述能力;分析推理能力
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2017)09-0071-02
【作者简介】闫颖,江苏省邳州市福州路小学(江苏邳州,221300)教务处副主任,一级教师,邳州市青年名教师,徐州市骨干教师。
几何直观是指利用图形描述和分析问题,它可以把复杂的数学问题变得简明、形象,帮助学生直观地理解数学,有助于学生探索解决问题的思路,在整个数学学习过程中发挥着重要作用。无论是数学概念、法则的学习,还是数学问题的解决,教师都可以借助几何直观发展学生的数学能力。
1.借助几何直观,发展概念表征能力。
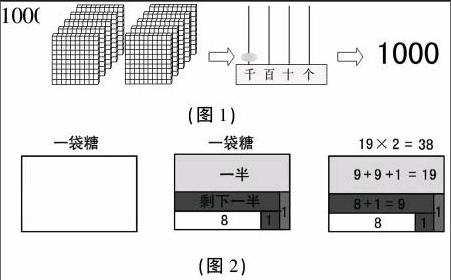
信息在人脑中有多种表征方式,而形象性的表征方式能有效促进学生对数学概念的理解。几何直观是一种特殊的、数学的直观,借助几何直观进行概念学习,是学生学习数学的有效途径。例如:教学苏教版二下《认识千以内的数》中“认识1000”时,教师一般引导学生认识10个1是10,10个10是100,10个100是1000,但是这样抽象的表述无法让第一学段的学生认识到1000究竟有多大。在教学中,教师应把教学重点放在1000的结构上,可以让学生通过数方格图,在脑中经历10个1是10,10个10是100,10个100是1000的过程。当学生头脑中形成了每层是100个小正方体,10层是1000个小正方体的形象时,让学生通过计数器表示出1000,最后学习如何书写“1000”这个数(如图1)。此时,学生对1000的认识才是深刻的。
2.借助几何直观,发展问题描述能力。
对小学生而言,以文字形式表述问题比较抽象。如果能把抽象的问题以直观图示的方式表示出来,把静态的文字转化为动态的图画,学生将易于发现条件与问题之间的关系。在教学中,教师可以引导学生合理运用画图策略,启发学生通过画几何图形来描述问题。如苏教版三上有这样一道思维拓展题:有一袋糖果,小红吃了这袋糖果的一半多1颗,小明吃了剩下糖果的一半多1颗,小强吃了剩下的8颗糖果,请问这袋糖果原来有多少颗?在解决这个问题时,如果不使用几何直观,学生很难形成清晰的表象与解题思路。教师可以引导学生通过画图,逐步还原题目中的条件(如图2),这将有助于学生快速地找到问题的正确答案。
几何直观在小学数学阶段应用很广泛,如使用线段图表示实际问题的数量关系,使用韦恩图(集合圈)表示长方形与正方形的关系,使用矩形图求面积,等等。
3.借助几何直观,发展分析推理能力。
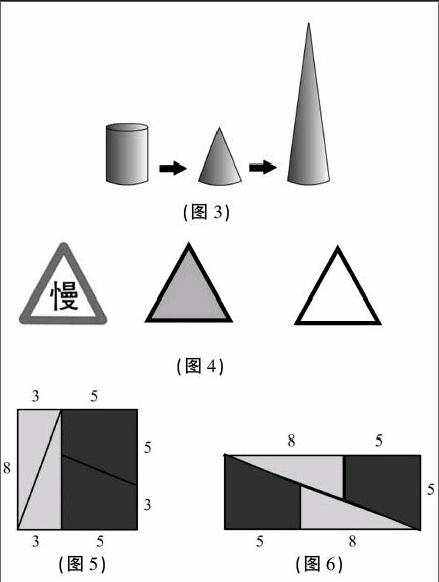
直观推理是数学直观的精髓。在教学中,教师应鼓励学生借助几何图形进行比较、分析和想象,让他们进行直观推理,进而探究出数学对象的结构和关系,建构数学结论。为了便于理解,学生可以在纸上画出相关图画和图表,将复杂的数学问题变形象,形成解决问题的思路。如苏教版六下有这样一道题:将一个底面积为9平方厘米,高为6厘米的圆柱体钢块熔铸成一个圆锥体。如果圆锥体和圆柱体的底面积相等,那么圆锥体的高是多少厘米?其实,在等底等高的情况下,圆柱的体积是圆锥体积的三倍。这道题的目的是考查学生能否活学活用知识,虽然难度不大,但是有相当多的学生并不理解此时圆柱与圆锥的高之间的关系,不能理解为什么圆锥体的高应当是18厘米。教师可以引导学生通过画图解决问题(如图3):
师:熔铸前后这两个形体有什么关系吗?
生:熔铸成的圆锥与圆柱体体积相等。
师:假设熔铸成的圆锥与圆柱体等底等高,那么这个圆锥体的体积与圆柱体体积有什么关系呢?
生:圆锥体的体积是圆柱体体积的三分之一。
师:如果要使圆锥与圆柱体体积相等,底面积不变,应当把圆锥怎么办呢?
生:只有把这个圆锥的高扩大三倍才能与圆柱体的体积相等,所以圆锥的高是18厘米。
对于正处于从形象思维向抽象逻辑思维过渡的小学生来讲,借助几何图形是比较有效的解决问题的策略。图像直观、形象、概括性强,有利于学生思考,如果学生能将某个问题转化成图像,就整体把握了这一问题。通过尝试画出草图,问题也就水到渠成地解决了。
4.避免几何直观的局限性。
借助几何直观可以帮助学生深入理解知识内涵,但在具体的运用中,应及时帮助学生从具体形象上升到抽象的数学概念,实现形象的剥离和认识的飞跃。例如:教学三角形、梯形、平行四边形和圆形等图形时,教师往往会让学生用硬纸板剪出这些图形。在这些直观形象的图形的暗示下,学生容易形成错误的认识:三角形就是三角形状这样的“平面”,平行四边形就是平行四边形状这样的“平面”,圆形就是一个圆面。在教学中,教师应及时抽象,将它们逐步过渡到抽象的几何图形。例如:在教学苏教版四下《认识三角形》时,教师可以先出示三角形实物,然后出示三条线段围成的图形,最终抽象出三角形的概念内涵(如图4)。
在发展学生直观思维的同时,教师应引导学生辩证地看待几何直观这一学习策略,避免将其“神圣化”。如解决下面这一问题时,学生将体验到几何直观的局限性:有一个边长为8厘米的正方形纸片,它的面积是64平方厘米。现在把这张纸片按图5所示剪开,把剪出的4个小块按图6所示重新拼合,就得到了一个长为13厘米、宽为5厘米的长方形,而这个长方形的面积是65平方厘米,比之前多出了1平方厘米,这是怎么回事?学生仅靠几何直观無法找出答案。
总之,几何直观能力的提升要从直观教学开始,教师要引导学生用画图的方法分析题意、解决实际问题,并逐步使学生将直观图形与数学语言、符号语言进行正确的转换。教师应有意识地安排教学,让学生反复练习,使几何直观这一思想方法转化为学生个体的学习习惯,如此,他们才能真正掌握和灵活运用这种数学思想方法。<\\Ysc02\d\邱\江苏教育\小学版\2017\02\KT1.TIF>

