基于LiDAR点云的地理电磁环境建模及仿真研究

王亚伟 钟选明 周亮 廖成

(西南交通大学电磁场与微波技术研究所,成都 610031)

引 言

随着信息化社会的发展,人们对通信质量的要求越来越高,无线电波作为信息传递的一种重要载体,其传播特性越来越受到人们的重视,准确地预测电波传播特性能够为基站的选址、网络的优化、电台的配置等提供有效的理论依据和工程指导[1]. 从20世纪70年代开始,国内外相关学者对电波传播特性预测展开了大量的研究工作,建立了很多的电波预测模型,如射线跟踪法、时域有限差分法等,但这些模型在处理复杂地理环境中的电波传播问题时难以在精度和效率之间达到一个很好的平衡. 由波动方程推导而来的抛物方程方法(Parabolic Equation Method, PEM)能够快速准确地处理复杂地表边界和复杂大气结构对电波传播的影响[2-3],在求解大区域复杂环境中的电波传播问题时得到了广泛的应用.

不规则的地形,多样化的地表覆盖物等是影响电波传播特性的主要因素. 目前,已有许多国内外学者基于抛物方程对地理环境中的电波传播问题展开了研究,Holm[4]、郭建炎[5]等人将森林视为有耗的介质层,采用二维抛物方程研究了不规则地形中森林覆盖环境下的电波传播问题,并与实测结果对比,验证了模型的正确性;张青洪[6]等人将森林看成空气和水的混合物,建立了森林等效介电常数模型,对抛物方程的森林模型进行了改进,这些研究一般考虑的地表环境比较单一,电磁建模也比较粗糙. 白瑞杰[7]等人基于数字高程模型对传播区域的电波特性做了预测分析,由于数字高程模型数据描述的是地形起伏的状况,缺少森林、植被、建筑等地表覆盖物的信息,难以满足城市小区域电波传播预测的电磁建模要求. 因此,研究更加接近真实场景下的电磁建模很有必要.

LiDAR点云是由机载激光雷达系统通过发射和接收激光脉冲获取的地表密集的高精度的三维点坐标,是对地形、地物特征的一种高精度的描述[8]. 通过对其分析处理,不仅可以获得地形起伏的信息,还可以获得植被、建筑等地物信息,将其应用于复杂地理环境的电磁建模,将会使电波传播的预测更加准确,因此本文研究了基于LiDAR点云的地理电磁环境建模. 采用数学形态学方法对格网化后的LiDAR点云做了滤波等处理,获取地形、地物等信息,结合相应物质的电磁参数,进行了地理环境的电磁建模,在此基础上,利用三维抛物方程模型对地理环境中的电波传播特性进行了仿真分析.

1 三维抛物方程模型

在笛卡尔直角坐标系中,假定电磁场的时谐因子为e-iωt,电场或磁场分量ψ满足如下形式的标量Helmholtz方程:

(1)

式中:n为媒质的折射指数;k0为自由空间中的波数.定义波函数u(x,y,z)=ψe-ik0x(x,y,z),将其代入式(1),并进行因式分解,可以得到

(2)

式(2)中,Q为伪微分算子,

(3)

仅考虑前向传播,对Q作Feit-Fleck型近似,可得到如下形式的三维抛物方程:

(4)

式(4)的数值解法主要为有限差分 (Finite Difference, FD[9]) 法和分步傅里叶变换 (Split-step Fourier Transform, SSFT[10]) 法,它们都是步进迭代算法. 其中FD算法的计算步长受波长严格限制,主要用于计算目标的雷达散射截面(Radar Cross Section, RCS)以及城镇小尺度电波传播特性的预测. SSFT算法引入了快速傅里叶变换(Fast Fourier Transform, FFT)技术,在传播方向上可以取较大的步长,能够快速地预测复杂地理环境中的电波传播特性,其解的形式如下[10]:

u(x+Δx,y,z)=eik0Δx(n-2)F-1{eikxΔxF[u(x,y,z)]}.

(5)

式中:kx表示k0在x方向上的分量;F和F-1分别表示二维傅里叶正逆变换.知道初始场,利用式(5)结合边界条件可迭代递推求得整个空间中的场强分布.

电磁波在空间远距离传输时,森林的影响是一个不容忽视的因素. 目前在研究森林对电波传播的影响时,通常把森林等效为均匀有耗的介质层[4-5],其等效的折射系数可表示成

(6)

式中:εr,σ分别表示森林的等效相对介电常数和电导率. 在迭代式(5)的过程中,通过式(6)不断地修正森林中的折射系数,则可处理森林中的电波传播问题. 通常森林中的等效折射系数趋近1,满足抛物方程的近似条件.

2 地理电磁环境建模

机载LiDAR是一种新型的主动式遥感技术,它通过测量激光脉冲的传播时间,结合POS系统提供的定位定姿数据,能够直接、快速获取地面的三维坐标[11]. LiDAR获取的点云文件记录了一系列被扫描物体表面的三维离散点坐标,其不规则地分布在三维空间中. 不同的地形、地物对应不同的激光脚点分布,反应到点云数据就会呈现出不同的几何拓扑形态. 通常情况下,地面点云的高程变化比较平缓,点的分布比较均匀;树木点云分布比较散乱,一般在边缘处会有高程突变;建筑物点云整体上几何形态较为规整,高程变化也较为一致. 水体对激光信号(波长为1 064 nm)的吸收,则会造成大面积的水体空洞区. 依据这些地物呈现出的不同特征,采用一定的技术手段可以对LiDAR点云数据进行分类.

2.1 点云滤波

点云分类中重要的一步是从点云数据分离出地面点和地物点,也就是点云滤波. 目前国内外学者提出许多种的滤波方法,其中具有代表性的算法有移动曲面拟合法、迭代三角网加密法、数学形态学方法等[10]. 为了适应抛物方程计算传播迭代步进的需要,本文采用了一种基于网格操作的数学形态学滤波算法[13].

数学形态学是一门建立在集合论的学科,目前已被广泛应用于各类图像分析和处理中,其基本操作有四种,分别为腐蚀、膨胀、开和闭运算. 对于LiDAR观测点p(x,y,z),膨胀(Dilation)运算和腐蚀(Erosion)运算分别定义为:

(7)

(8)

点(xp,yp,zp)表示在窗口(也称结构元)大小为w时点p的邻域点,理论上,窗口形状可以是任意的,实际处理中,我们通常选择简单的形状,如矩形、圆形、菱形等. 由式(7)、(8)可以推断出,膨胀运算和腐蚀运算分别能够获得邻域窗口内高程最大值和最小值. 基于膨胀和腐蚀运算,可以得到用于处理LiDAR数据的开运算和闭运算,开运算是先对给定的数据执行腐蚀运算,然后执行膨胀运算,闭运算则刚好相反.

数学形态学滤波的主要思想是将地物(树木、建筑物等)通过腐蚀运算腐蚀至地表,然后通过膨胀运算进行恢复[14]. 图1是采用线形结构元对点云数据的某一纵剖面执行开运算滤波的示意图. 当有多个点落入窗口中时,执行开运算后,将保留高程值最小的数据点. 由于树木的尺寸小于结构元尺寸,经过腐蚀后首先被去除,对于尺寸大于结构元的建筑物,则会在膨胀运算中得到重建.如果某点滤波前后的高程差在阈值范围内,则判定该点为地面点,否则判定为地物点,并标记. 可以看出,开运算能够很好分离出地物点以及地面点,并且能够获得较为平滑的地形.

图1 LiDAR点云开运算滤波示意图

结构元尺寸的选择决定了最终的滤波效果,当采用较小的滤波窗口时,尺寸大于窗口的地物(如建筑物)得不到很好的分离,采用较大的滤波窗口在分离地物的同时,也会过度地平整更多的地形特征,造成错误的分类. 由此可见,采用固定大小的滤波窗口很难对点云进行很好的分类,因此本文采用了线性渐进增大的滤波窗口.

2.2 点云分类

图2为某一地区的地理影像,图3为对应的原始LiDAR点云高程值图,区域中存在着大量的树木,右半部分有一个明显的河流空洞区.区域大小约为694 m×2100 m,点云高程差约为172 m,点云间距约1.2 m,共有1 717 762个离散点.

图2 地理影像图

图3 原始LiDAR点云高程值图

针对该区域的特点,采用以下流程将区域中的物质分为树木、地面、水三种类型.

1) 剔除噪点. 采用k邻近查询球[11]方法,剔除极低点、孤立点等高程异常值.

2) 点云格网化. 使用一个二维格网覆盖在LiDAR数据点上,格网间距通常略小于LiDAR点云密度,如果一个格网单元里有多个数据点,取格网单元中高程的最小数据点代表该格网单元的值,若网格单元中没有数据点的则不做处理[14].

3) 用二值图像表示格网后的点云数据,有值的网格单元高程值用“1”表示,否则用“0”表示. 用合适的“结构元”对二值图像执行闭运算. 经过闭运算后,小面积的空白区域将会被填充,剩下的空白就是大面积的水体造成空洞区,并标记.

4) 对非水体区域执行数学形态学滤波,判断滤波前后高程差阈值是否满足条件,分离出树木点和地面点.

5) 由地面点通过线性插值获得地形.

图4和图5分别为最终获得的地形以及分类结果.从图4中可以看出,在整个区域中,树木被很好地分离,而地形特征也保持相对圆满. 将图5对照原始地理影像图,可以看出,各种地物得到了很好的分类. 将二者结合起来,对各种地物赋上相匹配的电磁参数,就可以对上述地理环境进行电磁建模.

图4 地形图

图5 点云分类结果

3 电磁环境仿真

利用三维抛物方程模型预测上节所述地理环境下的电波传播特性.仿真参数设置如下:天线频率为900 MHz;高斯方向图3 dB带宽为10°;水平极化波;天线架设在横向距离为0 m,纵向距离为347 m,距离地表高度为45 m的地理环境处;大气条件为理想大气条件. 受限于数据源,最大传播距离为2 100 m,dy=dz=0.5 m,传播方向上的步长取dx=1 m.

图6显示了源所在的地形剖面上传播因子的分布情况,分别选取了(a)单一地表为黏性干土(介电常数为5,电导率为0.021 S/m)、(b) 真实的地理环境两种情况,其中地理环境中水的相对介电常数和电导率为81和0.22 S/m,树木的等效介电常数和电导率分别为1.004和180 μS/m[5]. 图6(a)中由于地形的存在,在地形后方出现了电磁波的盲区以及绕射现象,同时也可以看到由于地形的反射出现了明显的干涉条纹. 图6(b)中由于树木引起的遮挡,散射和吸收会产生较大的路径损耗,导致空间电磁波的整体损耗要大于没有树木时的情形,特别是在森林的内部,电磁波的损耗明显增大.

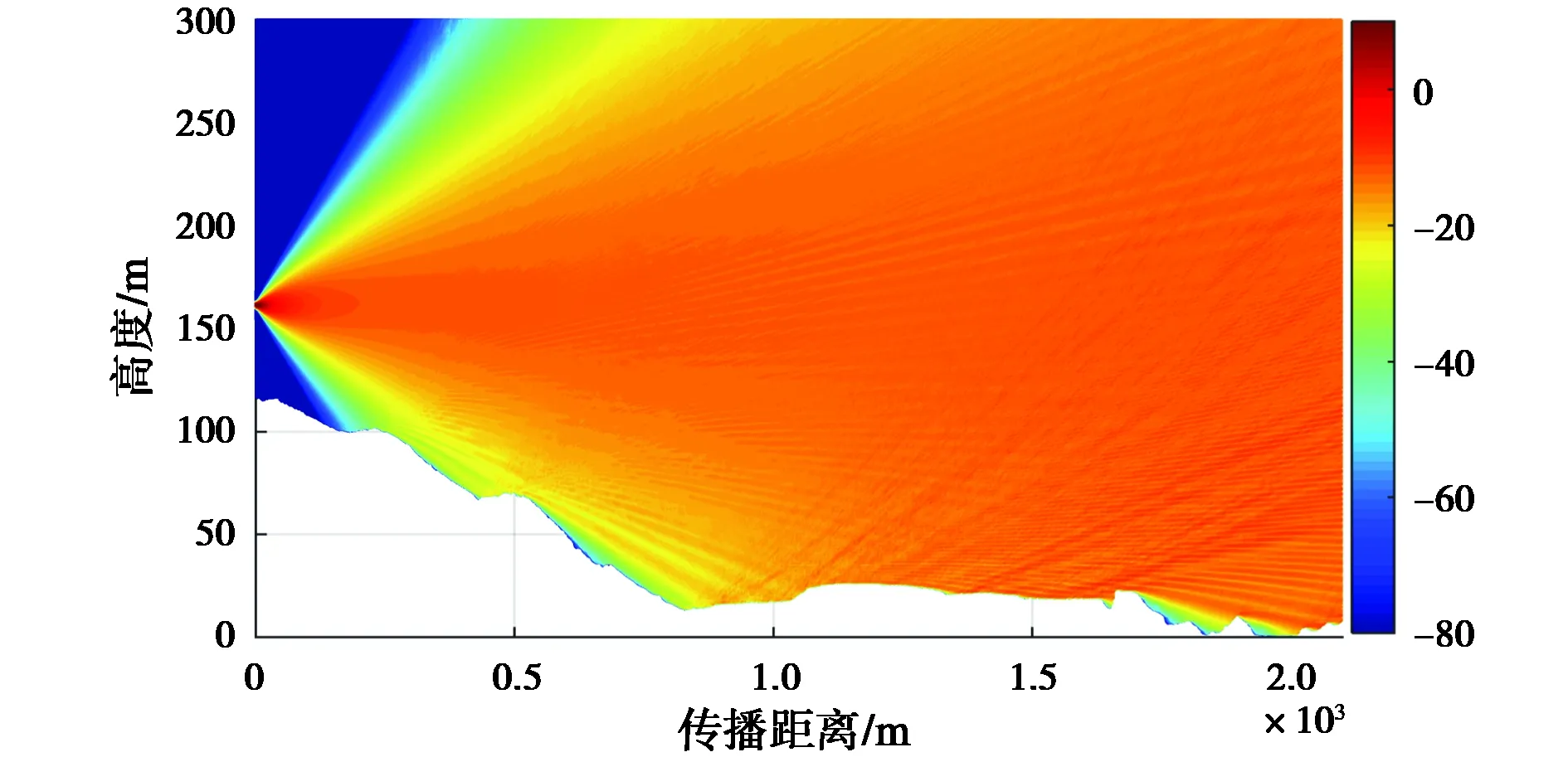
(a) 地表为干土

(b) 真实地理环境下图6 传播因子分布伪彩图

图8 两种算法下传播因子随高度的变化

图7为采用FD算法[15]计算得到的上述地理环境中传播因子的分布情况.与图6(b)对比,可以看出两者总体趋势大致相同,采用三维抛物方程能够考虑到电波的横向绕射,更加真实地反应出地理环境中电波传播特性. 图8显示了主辐射方向上,传播距离为2 100 m处,采用FD算法和SSFT算法得到的传播因子随高度的变化,两者吻合较好,说明了本文算法的正确性及有效性,SSFT算法相对于FD算法拥有更高的效率,能够快速地预测环境中的电波传播特性.

图9中显示的是主辐射方向上,传播距离一定时,有树木和无树木、有水无水的场景下传播因子随高度的变化情况.图9(a)是传播距离为2 000 m处,对比有树木和无树木情况下的传播因子.可以看出:在高度小于50 m的树木内部,电波的衰减较大;在远离树木的区域,电波的衰减相对较小. 图9(b)是传播距离为1 920 m处,有无水时传播因子随高度的变化曲线.从图中可以看出,两者相差很小,其主要原因是,水体的范围只有几十米,远离辐射源,电磁波成掠入射接触水体,并且水体前面存在着树木的遮挡作用,总体上水体对电磁波的传播影响较小.

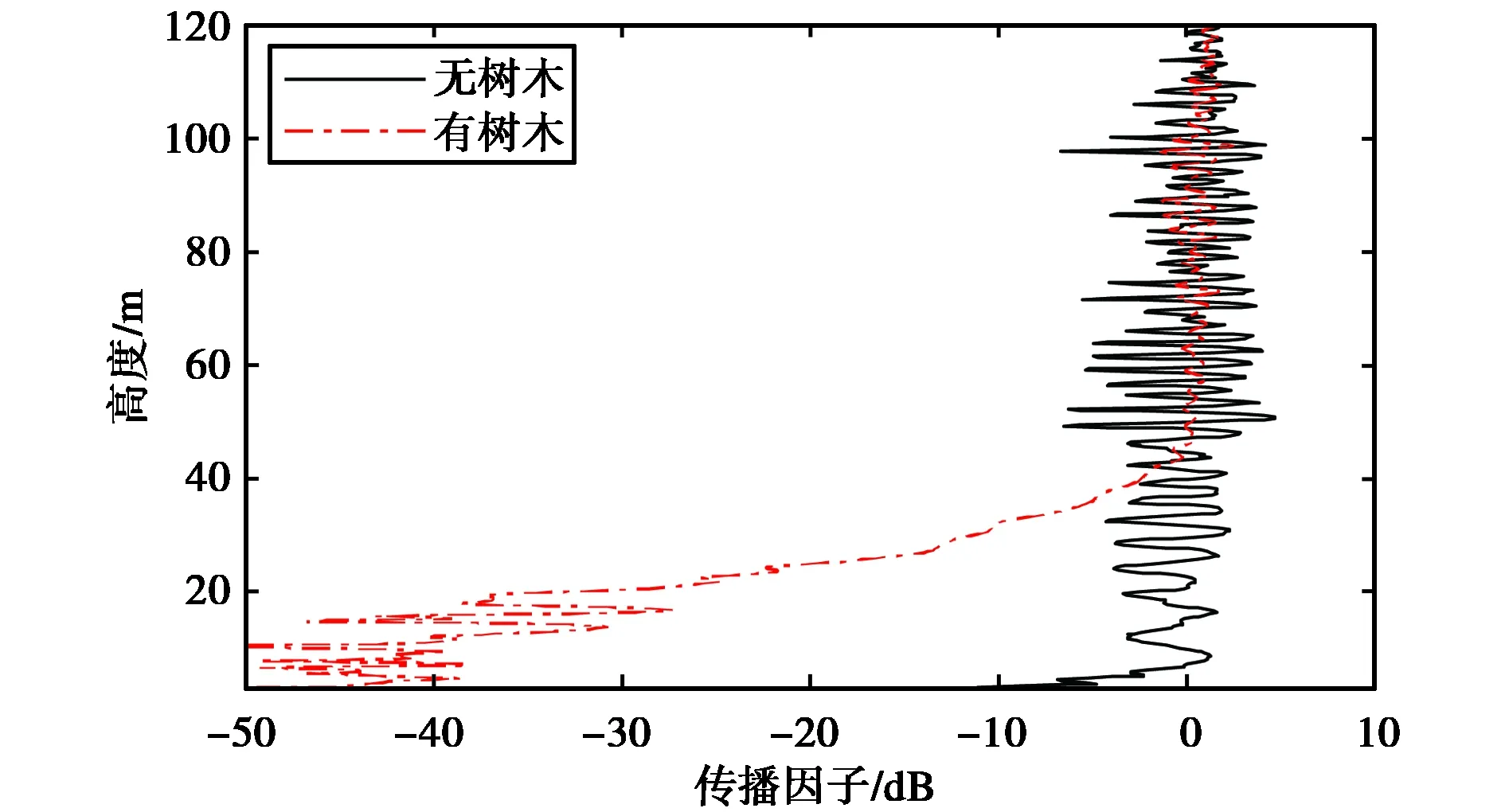
(a) 传播距离为2 000 m

(b) 传播距离为1 920 m图9 不同传播距离处传播因子随高度的变化

图10是在上述地理环境中,发射天线分别架设在距离地面高度35 m、45 m和55 m的情况下,距离发射天线2 100 m处的传播因子随高度的变化情况. 通过比较可以看出,在一定接收高度下,电波的衰减随着发射天线架设高度的增加而减小,因此适当把天线架设在高处,可以减小到达接收点的信号衰减,扩大无线信号的覆盖范围.

图10 不同天线高度下传播因子随高度的变化

4 结 论

本文研究了基于LiDAR点云的PEM电波传播模型,针对传统地理电磁环境建模的不足,研究了LiDAR点云数据中地物分类,对传播区域的地理电磁环境进行了更为准确的建模,并采用抛物方程模型对有地表覆盖物的环境下电波传播特性进行了仿真分析. 相对于传统的电磁建模方法,本方法能够考虑到地表覆盖物对电波的影响,从而更真实地反映出电波的传播特性. 下一步的工作重点是在现有的基础上,研究包含建筑物、树木的复杂城区的LiDAR点云分类,并结合大气环境对区域中的电波传播特性进行预测.

[1] DUMONT N, WATSON R J, PENNOCK S R. Use of the parabolic equation propagation model to predict TV white space availability[C]//Antennas and Propagation Conference. Loughborough, November 8-9, 2010: 353-356.

[2] LEONTOVICH M, FOCK V. Solution of the problem of propagation of electromagnetic waves along the earth’s surface by the method of parabolic equation[J]. Journal of physics USSR, 1946(7): 557-573.

[3] DONOHUE D J, KUTTLER J R. Propagation modeling over terrain using the parabolic wave equation[J]. IEEE transactions on antennas & propagation, 2000, 48(2): 260-277.

[4] HOLM P, WAERN A. Wave propagation over a forest edge parabolic equation modelling vs. GTD modelling[C]//IEEE International Symposium on Electromagnetic Compatibility. Istanbul, May 11-16, 2003: 764-767.

[5] 郭建炎, 王剑莹, 龙云亮, 等. 基于抛物方程法的部分森林覆盖山区电波传播分析[J]. 电波科学学报, 2008, 23(6): 1045-1050.

GUO J Y, WANG J Y, LONG Y L, et al. Analysis of radio propagation in partly forested terrain environment using parabolic equation approach[J]. Chinese journal of radio science, 2008, 23(6): 1045-1050. (in Chinese)

[6] 张青洪, 廖成, 盛楠, 等. 森林环境电波传播抛物方程模型的改进研究[J]. 物理学报, 2013, 62(20): 204101.

ZHANG Q H, LIAO C, SHENG N, et al. Improved study on parabolic equation model for radio wave propagation in forest[J]. Acta physica sinica, 2013, 62(20):204101. (in Chinese)

[7] 白瑞杰, 廖成, 张青洪,等. 复杂地理环境的图像分割及电波传播特性[J]. 强激光与粒子束, 2015, 27(10): 63-67.

BAI R J, LIAO C, ZHANG Q H, et al. Image segmentation of complex geographical environment and wave propagation characteristics[J]. High power laser and particle beams, 2015, 27(10): 63-67. (in Chinese)

[8] 陈松尧, 程新文. 机载LIDAR系统原理及应用综述[J]. 测绘工程, 2007, 16(1): 27-31.

CHEN S Y, CHENG X W. The principle and application of airborne LIDAR[J]. Engineering of surveying and mapping, 2007, 16(1): 27-31. (in Chinese)

[9] LEVY M. Parabolic equation methods for electromagnetic wave propagation[M]. London: IEE Press, 2000: 35-40.

[10] HARDIN R H, TAPPERT F D. Application of the split-step Fourier method to the numerical solution of nonlinear and variable coefficient wave equations[J]. SIAM review, 1973, 15(423): 423.

[11] 成晓倩, 马洪超, 赵红强,等. 一种基于区域增长的机载LIDAR滤波[J]. 测绘科学, 2010, 35(1): 61-63.

CHEN X Q, MA H C, ZHAO H Q, et al. A filtering of LIDAR based on region growing[J]. Science of surveying and mapping, 2010, 35(1): 61-63. (in Chinese)

[12] ZHANG W, QI J, WAN P, et al. An easy-to-use airborne LiDAR data filtering method based on cloth simulation[J]. Remote sensing, 2016, 8(6): 501.

[13] PINGEL T J, CLARKE K C, MCBRIDE W A. An improved simple morphological filter for the terrain classification of airborne LIDAR data[J]. ISPRS journal of photogrammetry & remote sensing, 2013, 77(1): 21-30.

[14] ZHANG K, CHEN S C, WHITMAN D, et al. A progressive morphological filter for removing nonground measurements from airborne LIDAR data[J]. IEEE transactions on geoscience & remote sensing, 2003, 41(4): 872-882.

[15] DING W, WANG K, LONG Y. Study of the electromagnetic waves propagation over the improved fractal sea surface based on parabolic equation method[J]. International journal of antennas and propagation, 2016(3): 1-7.