基于真实地形的高压线电场的数值模拟

侯宇 李保珠 陆振君 侯奋飞,2

(1. 南京师范大学物理科学与技术学院,南京 210023; 2. 江苏省地理信息资源开发与利用协同创新中心,南京 210023)

引 言

近年来,随着超高压电网在全国覆盖面逐渐扩大,由高压电力设备带来的电磁环境问题日益激增[1]．其中高压输电线路产生的工频电场污染引起了人们的广泛关注[2]．国家对基础设施的环境标准越来越严格,为了评估高压线对环境的影响是否过大[3-4],有必要准确地计算高压线路产生的电场．

通常以把大地看作平面为前提来计算输电线路产生的工频电场．但事实上,输电线路的架设路线很可能会经过山地或斜坡,起伏地形将会对输电线路的电磁环境产生重大影响．如文献[5]应用模拟电荷法研究了不平坦地形对高压线电磁环境的影响,文献[6]利用表面电荷法分析表明地面形状不同会导致电场分布的不同,文献[7]通过有限元仿真表明500 kV高压线下地面近似为水平面的电场最大值小于凹面和凸面的电场最大值．可以看出,不平坦地形对地表电场分布存在较大影响．

为了对高压线下的工频电场进行预测分析,除了实测手段[8-11]外普遍采用数值模拟的方法．如文献[12-13]利用有限元分析软件ANSYS对不同地形对电场的影响做了仿真分析．文献[5]使用ACEME3.0(AC Electromagnetic Environment 3.0)对高压线下电场分布进行了仿真与分析．不过,以上研究都假定地面为理想化的二维模型,难以等效实际地形下地表电场的分布情况,所得实际参考价值也受到一定的影响．并且有限元法必须假定值在网格之间的变化规律,将其作为近似解,对复杂问题的分析耗费的资源相当多,不适合大尺度计算,所以以上文献均局限于小尺度模拟域的电场计算．而有限差分法只考虑网格点上的数值而不考虑值在网格点之间如何变化,耗费的资源相对较少．

本文为分析地形对高压输电线周边地表电场分布的影响,采用不等距有限差分法,结合数字高程模型(Digital Elevation Model,DEM)地形数据建立220 kV高压交流输电线路的物理模型,进行三维电场计算分析．其中输电线产生的工频电场主要在地面附近区域,受到地形的显著影响并且影响人类的活动．所以本文重点研究高压线在近地面处产生的工频电场．最后将仿真数据与测量结果进行比较以验证可靠性,可以为高压交流输电线路经复杂地形架设时,在线路走廊设计和电磁环境分析方面提供参考和依据．

1 计算方法简介

对于空间电场的计算,归根到底是如何解决泊松方程的问题．目前,普遍使用的数值解法包括模拟电荷法[14-15]、有限元法[16]以及有限差分方法[17-18]等．模拟电荷法适用于边界形状简单,大地为平面的情形．有限元对物理模型进行离散化,分割为许多的元素和节点,计算速度慢．因此,本文拟选用有限差分法．

1.1 高压输电线路模型简化

为便于计算和分析,高压线路模型被简化如下:1)交流输电线路所产生的正弦时变电磁场被视为准静态场;2)忽视铁塔、绝缘子和金具对线路电场分布的影响;3)大地视为良导体,电位为零．

1.2 三维电场的不等距有限差分法

空间电位分布满足泊松方程:

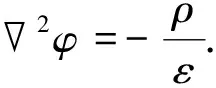
(1)

在直角坐标系下表示为

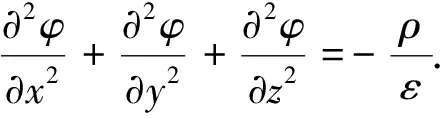
(2)

式中:ε为介电常数;φ为电势;ρ为自由电荷密度．在没有自由电荷的区域中,ρ=0,这时泊松方程就简化成拉普拉斯方程,即

(3)

将求解区域内连续的电位函数以离散节点上的电位值表示,采用7点差分格式,中间点0由周围的6个点来确定．这里我们对原有的有限差分方程做了改进,x、y、z方向上采用不同距离的步长,分别为h1、h2、h3,如图1所示．

图1 不等距离7点差分格式示意图

式(2)通过Taylor级数展开,再整理,得

(4)

(5)

在得到每个节点的电位数值后,再对电位求梯度即得到电场:

E=-φ.

(6)

使用不等距有限差分可以实现同一空间不同大小网格的剖分,增强有限差分算法的灵活性,适应真实地形下的网格划分需要．

1.3 边界条件

本文中,空间计算模型的边界条件为:

φ|φ=0=0,

(7)

φ|φ=U=U.

(8)

式(7)的含义为在大地或者无限远处空间电位始终为零(当边界距离场源较远时可近似为无穷远)．式(8)含义为高压线导体(场源)表面电位为线路运行电压U．

1.4 输电线

交流高压输电线呈悬链线形状,电压用相量的形式来表示．如图2,根据三相回路各相的相位和分量计算各导线对地电压为:

(9)

各导线对地电压幅值以额定电压的1.05倍作为计算:

(10)

式中,U为线电压．

图2 各相对地电位计算图

1.5 地形剖分方法

本文提出了对DEM地形数据使用“阶梯”近似的方法进行网格剖分来逼近真实地形．DEM是通过用一组有序数值阵列形式表示地面高程的一种实体地面模型．图3中,空间被剖分为网格,地形数据为黑色节点．将黑色节点在高度方向上平移到与之最近的网格节点上(红色节点),将红色节点依网格相连产生阶梯地面,以红色线条表示的阶梯地面逼近黑色线条表示的真实地面．地形DEM数据包含地形水平坐标和高度坐标,对于水平坐标使用如下公式进行坐标网格转换,划分为规则矩形网格:

横坐标x=a×(E-Emin)/(Emax-Emin),

纵坐标y=b×(N-Nmin)/(Nmax-Nmin).

式中:a,b为矩形网格范围;Emax、Emin为地图经度极大值、极小值;Nmax、Nmin为地图纬度极大值、极小值;E、N为地面经纬度坐标;x,y为将经纬度转化后的水平横纵坐标．

图3 阶梯近似示意图

对高度坐标以空间网格在z方向上的间距为单位进行近似处理．例如,本文中空间网格在z方向间隔为1 m,则需要对高度坐标进行取整以适应空间网格的需要,使得处理后的地形高程数据为离散整数．如此便完成对地形数据的剖分．

用阶梯形网格代替不规则边界曲面的近似方法难免带来计算精度误差,但理论上只要空间网格划分足够精细,便能接近真实地形．由于本文空间网格高度间隔以米为单位,所以这种近似方法下阶梯地面与真实地面高度误差不会超过1 m,属于可以接受的范围．处理过后的地面数据由示意图(图4)中红色节点组成,为离散数据．此外,还可以使用双线性内插法对地形数据进行差值以提高地形数据的精度．

图4 地形数据插值前后比较

1.6 方法验证

采用不等距有限差分方法将求解区域划分为离散网格计算高压线周边电场分布,需要验证计算结果是否与模拟电荷方法一致,并且考虑对空间做不同大小网格划分对计算结果造成的影响．

建立三维输电线模型(图5),高压线电压等级220 kV,呈正三角布置形式,边相距地高度30.89 m,中相距地高度39.49 m,边相与中相水平间距为7.5 m,线路档距367 m,最大弧垂约为5 m．空间范围600 m×600 m×50 m,分别从x,y,z方向对空间进行不同间距的网格划分．分别用有限差分法和模拟电荷法计算档距中央处地表(y=300 m,z=2 m)电场分布并生成曲线,结果如图6所示．

由图6可知:有限差分网格Δx=Δy=Δz=0.1 m时与Δx=Δy=Δz=1 m产生的结果几乎完全重合;当Δz=1 m不变,Δx=Δy等于1 m和2 m时有限差分法曲线与模拟电荷法曲线基本吻合,可以验证本文方法的正确性．还可以看出,距离中相高压线对地投影点约20 m范围以外时,采用不同间距网格计算得到的电场结果基本重合,则空间网格剖分对仿真结果的影响很小,不需要对空间做很精细的网格剖分就能得出较为准确的结果．距离中相高压线对地投影点约20 m范围以内时,不同间距的网格剖分对仿真结果的影响较大,如果想要得到较为精确的结果则需要对空间做更为精细的网格剖分．

图5 高压线模型

图6 不同间隔时离地高度2 m处的电场曲线

2 模拟算例及分析

2.1 模型的建立

本文模拟区域的范围为南京栖霞仙林地区羊山湖附近长3.75 km,宽3.6 km,海拔0 m到300 m的真实地形包括了盆地、山体、平原等．地形DEM数据精度为30 m,我们采用双线性内插法将地形数据精度插至5 m,如图4(颜色代表高度)所示．还有三条该地区主要的220 kV级双回路高压输电线走廊,走廊长度约3 km,总共20根杆塔．杆塔具体分布位置如图7(红线为走廊,灰点为杆塔)所示,每一条走廊包含六根导线．杆塔模型如图8所示,最低相导线离地面高度15 m．将整个空间均匀划分为750×714×300个空间网格,每个网格大小为5 m×5 m×1 m(x,y方向5 m,z方向1 m),依据真实高压线塔建立模型设置场源．完成模型建立后运用不等距有限差分法进行迭代运算．同时为保证实验结果的准确性,对实测线路附近小范围区域采用分米级大小网格(1 dm×1 dm×1 dm)进行划分计算,所得结果如图9所示．

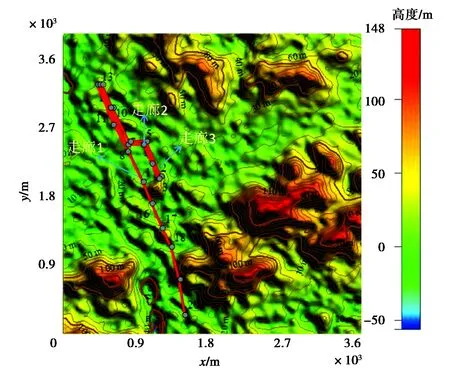
图7 高压线走廊地形示意图

图8 高压线杆塔模型示意图

2.2 实际电场测量

测量仪器采用设备如下:频谱仪(6台,安捷伦),主要用于射频和微波信号的频域分析,包括测量信号的功率、频率、失真产物等等．电磁探头(4台,nardadll 50D,200A),主要用于测量电磁信号的强度．图9绘出了实测线路以及仿真数据与实测数据的结果比较．

(a) 实测线路1示意图

(b) 实测线路2示意图

(c) 实测线路1于仿真区域所处位置

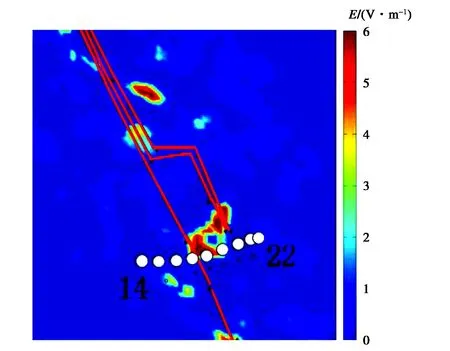
(d) 实测线路2于仿真区域所处位置

(e) 实测线路1地形走势图

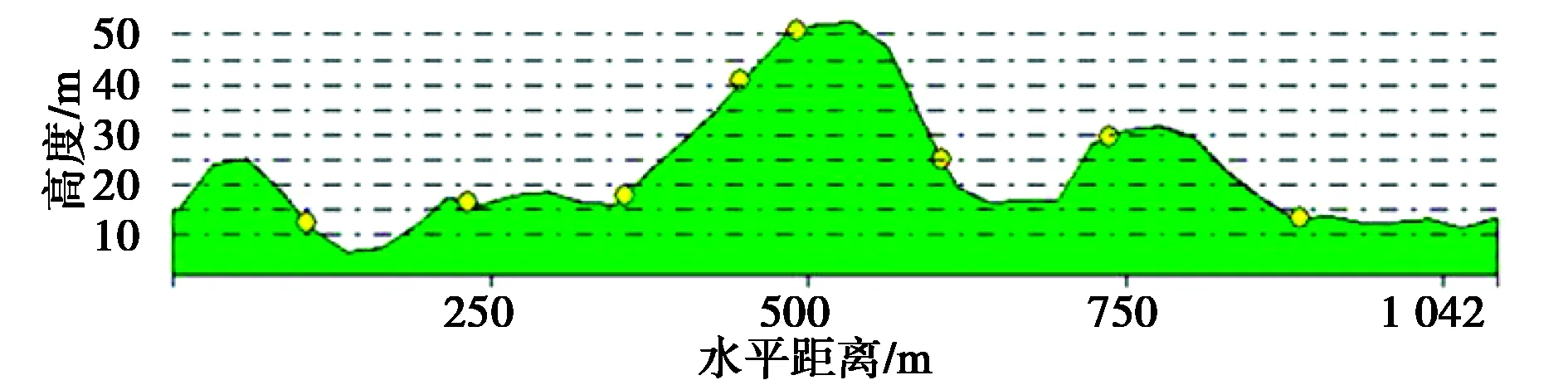
(f) 实测线路2地形走势图

(g) 实测线路1实测与仿真结果比较

(h) 实测线路2实测与仿真结果比较 图9 线路仿真结果验证

2.3 结果分析

本节分别取测量点1至13,14至22两条测量路线对高压线附近电场进行测量．根据车载仪器高度给出了离地3 m的电场强度仿真结果,红色线条表示高压线走廊．整个羊山湖附近区域场强分布结果如图10所示．图11为地表电场分布的3D示意图．

图10 场强仿真结果

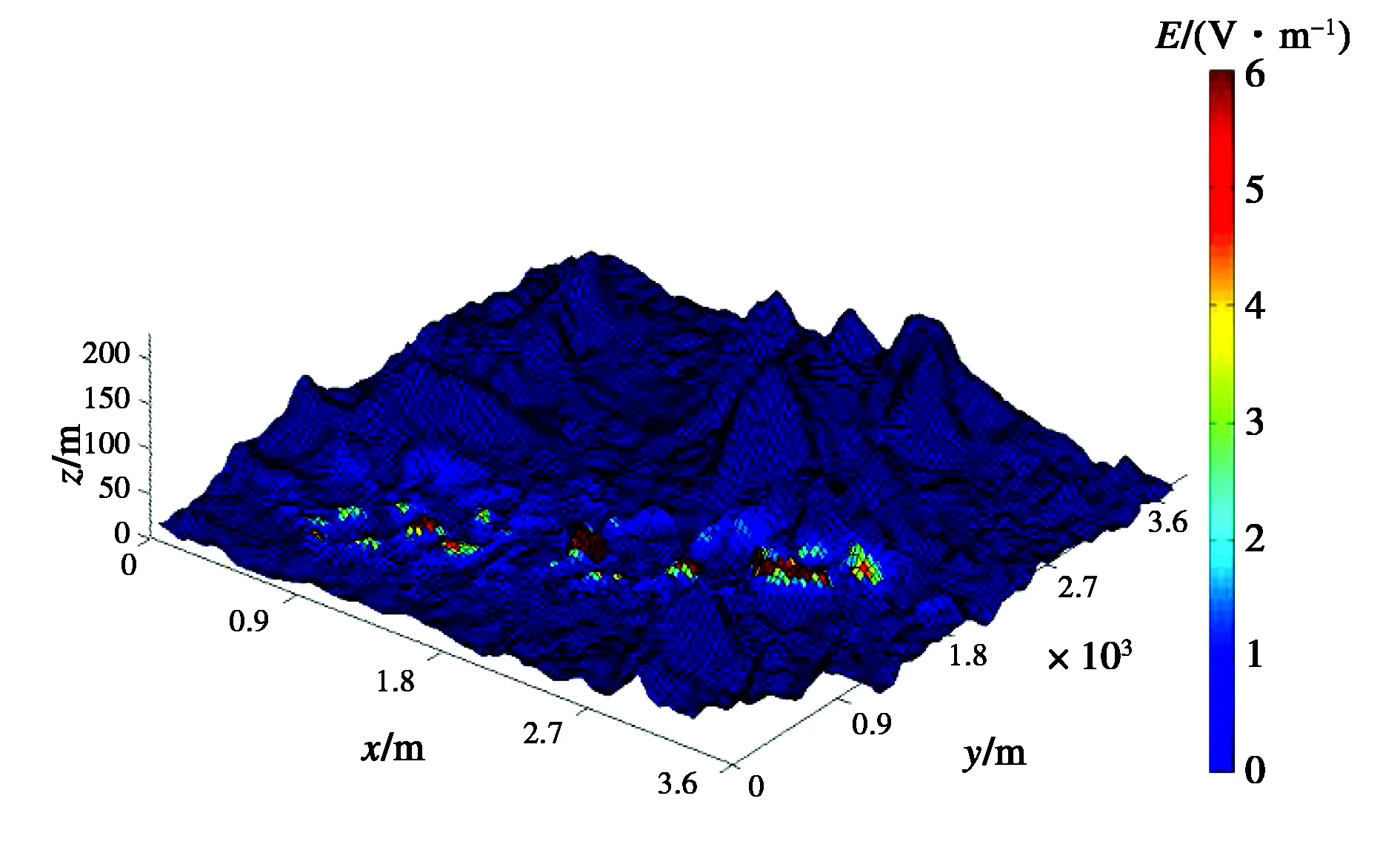
图11 地表电场分布3D示意图

从仿真结果来看:几处红色区域所处地形均为高地,低洼地形地表电场值在图中则大多呈现为蓝色,斜坡地形处电场值则居于两者之间;高压线近场电场畸变较为明显,其电场值要高于远场电场值;高压线附近高地处地表电场明显高于洼地;高压线下高地处地表电场最强．地势的起伏造成线路周围地表电场分布的不均匀,这在高压输电线路走廊的规划中是一个很值得注意的现象．

一般认为大地电位为零．地表电场在计及大地电位后会产生扭曲,在加入复杂地形以后便体现为地表电场的不均匀性．可见地形对于空间电场的显著影响,进一步认识到加入地形因素对于分析高压线周边电场以及电磁环境研究的必要性．

3 总 结

针对实际高压线路架设走廊中地形对高压线附近电场分布的影响,本文提出了不等距有限差分法以及对地形进行阶梯近似的方法并加入了三相交流电,利用有限差分与地形剖分相结合计算复杂地形下高压输电线路的空间电场分布,该方法能够实现真实地形下高压输电线路三维空间电场的数值仿真．将仿真数据与实测结果进行对比,验证了仿真结果的可靠性,并且可以看出地形对地面附近工频电场存在明显影响．该方法建模所得结果,可为高压输电线路在复杂地形架设时,线路走廊的设计和电磁环境的分析评估提供参考．

[1] 吴敬儒, 徐永禧. 我国特高压交流输电发展前景[J].电网技术, 2005, 29(3): 1-4.

WU J R, XU Y X. Development prospect of UHV AC power transmission in China[J]. Power system technology,2005,29(3):1-4.(in Chinese)

[2] 吴桂芳,陆家榆,邵方殷.特高压等级输电的电磁环境研究[J].中国电力,2005,38(6): 24-27.

WU G F, LU J Y, SHAO F Y. The electromagnetic environment research of ultra high pressure level[J]. China power,2005,38(6):24-27. (in Chinese)

[3] 许杨,张小青,杨大晟.高压输电线路工频电磁环境[J].电力学报,2007,78(1):10-12.

XU Y,ZHANG X Q, YANG D S. High voltage transmission line power frequency electromagnetic environment[J]. Journal of electric power, 2007,78(1):10-12.(in Chinese)

[4] 惠建峰,关志成,刘瑛岩.各国工频电磁场的限值及其确定的依据[J].高电压技术,2006,32(4):51-54.

HUI J F, GUAN Z C, LIU Y Y.Countries of the limit of power frequency electromagnetic field on the basis[J]. High voltage technology, 2006,32(4):51-54.(in Chinese)

[5] 周宏威,左鹏,邹军,等.复杂地形情况下高压交流输电线路电磁环境特性分析[J].电网技术,2011,35(9): 165-168.

ZHOU H W, ZUO P, ZOU J, et al. The analysis of the high voltage transmission line electromagnetic environment feature under complicated terrain[J]. Power system technology,2011,35(9):165-168.(in Chinese)

[6] 郭菲.复杂地势下超高压交流输电线路的工频电场仿真计算[D].济南:山东大学,2014.

GUO F. The simulation of power frequency electric field of the EHV ac transmission line under the complex terrain[D].Ji’nan: Shandong University,2014.(in Chinese)

[7] 吴小雁,薛毓强,黄云程,等.考虑复杂地势的交流超高压输电线路电场[J].电气技术,2015,16(9):7-11.

WU X Y, XUE Y Q, HUANG Y C, et al. Considering the complex terrain of ac electric field distribution of super-high voltage transmission line[J]. Electrical engineering,2015, 16(9): 7-11.(in Chinese)

[8] 傅艳军.110kV变电所工频电场测量与分析[D].上海:上海交通大学,2005.

FU Y J. The measurement and analysis of 110kV substation power frequency electric field[D].Shanghai: Shanghai Jiao Tong university,2005.(in Chinese)

[9] 张婷,方志,陈陶陶,等.球形电场测量系统在高压测量领域中的应用[J].电测与仪表,2007,44(11):11-16.

ZHANG T,FANG Z,CHEN T T, et al. The spherical electric field measurement system application in the field of high voltage measurement[J].Electrical measurement and instrumentation,2007,44(11):11-16.(in Chinese)

[10] 唐海.雷电预警系统中大气电场仪的研究与设计[D].南京:南京信息工程大学,2009.

TANG H. The research and design of the lightning warning system of atmospheric electric field instrument[D].Nanjing: Nanjing Information Engineering University,2009.(in Chinese)

[11] 胡泽文,何为.高压工频电场警示仪的研究[J].电测与仪表,2009,46(9): 45-48.

HU Z W,HE W. Warning device of high-voltage power frequency electric field research[J].Electrical measurement and instrumentation, 2009,46(9):45-48.(in Chinese)

[12] 彭湃,程汉湘,陈杏灿,等.基于有限元的超高压输电线路电场的数值分析与测量[J].电测与仪表,2016,53(3):56-61.

PENG P, CHENG H X,CHEN X C, et al. The numerical analysis and measurement of electric field of super-high voltage transmission line based on the finite element[J]. Electrical measurement and instrumentation,2016,53(3):56-61.(in Chinese)

[13] 谭涌波,张冬冬,郭秀峰, 等.轴对称建筑物形状对电场畸变影响的数值模拟[J].电波科学学报,2014,29(6): 1219-1224.

TAN Y B,ZHANG D D, GUO X F, et al. Numerical simulation of effects of shape of axial symmetry buildings on electric field distortion[J]. Chinese journal of radio science,2014, 29(6):1219-1224.(in Chinese)

[14] 俞集辉,周超. 复杂地势下超高压输电线路的工频电场[J].高电压技术,2006,32(1): 18-24.

YU J H,ZHOU C. The power frequency electric field of EHV transmission line under the complex terrain[J]. High voltage technology, 2006,32(1):18-24.(in Chinese)

[15] GUO F, LIANG Z G, JIANG Y Z.Power-frequency electric field calculation of extra high voltage transmission lines under condition of complex landscape[C]//International Conference on Computer Science and Network Technology. Dalian: IEEE, 2014:37-41.

[16] YANG B, WANG S H, WANG Q, et al. Simulation and analysis for power frequency electric field of building close to power transmission lines[C]//International Symposium on Electromagnetic Compatibility. Raleigh: IEEE, 2014:451-454.

[17] SHAO W, WANG B Z, YU Z J. Space-domain finite-difference and time-domain moment method for electromagnetic simulation[J]. IEEE transactions on electromagnetic compatibility, 2006, 48(1):10-18.

[18] NAGEL J R. Numerical solutions to poissonequations using the finite-difference method[J]. IEEE antennas and propagation magazine, 2014, 56(4):209-224.