海啸波对近岸岛礁影响的数值模拟研究

任智源， 赵曦， 闪迪， 王培涛

(1. 国家海洋环境预报中心， 北京 100081; 2. 国家海洋局海啸预警中心， 北京 100081; 3. 上海交通大学 工程力学系， 上海 200240)

海啸波对近岸岛礁影响的数值模拟研究

任智源1，2， 赵曦3， 闪迪1，2， 王培涛1，2

(1. 国家海洋环境预报中心， 北京 100081; 2. 国家海洋局海啸预警中心， 北京 100081; 3. 上海交通大学 工程力学系， 上海 200240)

基于Okada有限断层模型和非线性浅水波方程，结合高精度嵌套网格建立了越洋(中国近海)-局部-近岸岛礁的海啸生成与传播的数值模型。以三亚凤凰岛为例，首先针对2011日本地震海啸，模拟分析了海啸波沿中国沿海大陆架的传播特征及对凤凰岛的影响规律。在取得验证结果的基础上，进一步讨论了中国近海的马尼拉海沟和琉球海沟的潜在海啸源，以及环太平洋的21个潜在特大越洋海啸对凤凰岛的影响特征。依据海啸波在抵达凤凰岛的波浪特征，结合傅里叶频谱分析方法，探索了近岸岛礁对海啸波的放大效应。结果表明，中国近海一般震级的海啸和特大越洋海啸对凤凰岛存在一定影响，最大波幅接近1 m，传播时间从3 h到27 h不等。受三亚东南半岛的影响，琉球海沟激发的海啸和越洋海啸在凤凰岛的放大效应相对于马尼拉海沟较小，其频率集中在0.8×10-4～2×10-4Hz。马尼拉海沟产生的海啸波在凤凰岛产生了较为显著的放大效应，对于凤凰岛是值得关注的高风险海啸源。

海啸波；近岸岛礁；数值模拟；凤凰岛；放大效应

1 引言

近十几年来，以2004年印度洋海啸和2011日本地震海啸为代表的特大地震海啸事件对沿海地区造成了极大的人员伤亡、财产损失和环境破坏[1—4]。由于在早期缺乏必要的海啸预警系统，同时海啸波在深水中的传播速度极快(波速c=gh，如果是4 000m的平均水深，传播速度达到713km/h，接近喷气式飞机的速度)，因此人们在面对这样的极端海洋灾害时往往难以应对。改善海啸预警方法、发展海啸数值模型、评估潜在海啸源可能引发的海啸灾害、研究海啸波的爬高淹没规律、分析海啸波对海岸结构物的水动力载荷，成为了海啸研究的主要关注方向[5]。

海啸不仅会对海岸带产生极大破坏，对岛礁也会带来一定威胁。1992年12月12日，印度尼西亚Flores岛附近发生了震级Ms=7.5的地震，引发的海啸导致Babi岛背浪面产生极大的海啸波，致使两个村庄被摧毁，死亡700多人[6]。1993年7月12日，日本Okushiri岛附近发生7.8级地震所激发的海啸波产生在岛上产生了超过30 m的爬高[7]。相比于深海岛礁，近岸岛礁不仅由于水深变浅导致波浪的浅化和破碎[8—9]、非线性效应增强，同时海岸的影响使海啸波产生更为复杂的水动力特征。Berger等[10]和Stefanakis等[11]利用非线性浅水方程针对概化模型研究了海啸波与近岸岛礁的相互作用，发现由于近岸的反射和波浪绕射作用，在岛礁的背浪面发生了聚焦，波高明显增大。但真实的近岸岛礁地形结构复杂，海啸波在复杂地形条件下对岛礁的影响规律是本文所关注的研究内容。

尽管2011日本地震海啸对中国沿海的影响不大，最大波幅仅为0.5 m左右[12—13]，但作为一次距离中国沿海较近的典型的海啸事件，有必要分析其沿中国沿海的传播特征及对近岸岛礁的影响。海啸的数值传播模型主要有浅水波模型和Boussinesq模型。第一类以康奈尔大学的COMCOT、华盛顿大学的GeoClaw，以及美国国家海洋和大气管理局的MOST为代表。第二类基于Boussinesq方程的数值模拟主要为特拉华大学的FUNWAVE和康奈尔大学的CULWAVE。Glimsdal等基于色散模型研究了多个典型的海啸事件，发现海啸波传播的色散效应与水深、传播距离等多个因素有关[14]。Ren等基于耦合海啸生成模型与Boussinesq模型，分析了南海Mw=8.0和Mw=9.3级潜在地震海啸的波面特征，发现由于地形和水深的影响，南海潜在海啸同样存在一定的色散效应[15]。Ren等[12]在对2011日本地震海啸的模拟研究中发现，底摩擦效应(曼宁系数)对深水传播过程没有影响；Kirby等[16]通过研究发现，海啸在传播过程中，科氏力是可以忽略的。海啸从深海经过大陆架向近岸的传播过程中，水深变浅使得波浪的非线性效应变得逐渐明显[17—18]。因此本文采用非线性浅水波模型研究海啸波对近岸岛礁的影响规律是可行的。

本文选取了海南省三亚市凤凰岛作为研究对象。凤凰岛是在大海礁盘之中吹填出的人工岛，全长1 250 m，宽约350 m，占地面积36.5万m2。该岛四面临海，东面距离最近的陆地仅300 m，南面受三亚延伸到南海的半岛所保护。本文利用基于非线性浅水波数值模型和高精度嵌套网格，以三亚凤凰岛为例，模拟研究海啸波对近岸岛礁的影响。首先针对2011日本地震海啸，结合实测数据分析海啸波在生成之后沿中国沿海大陆架的传播过程及对凤凰岛的影响特征。进一步研究总结中国近海的马尼拉海沟和琉球海沟潜在震源，以及环太平洋的21个潜在特大地震源，所激发的海啸对凤凰岛可能造成的影响。根据海啸波的功率谱密度特征，初步探讨海啸波在近岸岛礁的放大效应。基于海啸的波浪特征，为近岸人工岛礁的设计、建设，与防护提供水动力学方面的参考。

2 控制方程及计算方案

2.1 控制方程

本文采用基于平面二维非线性浅水波方程的数值模型(GeoClaw)模拟研究海啸波的传播过程[19]。控制方程可以表示为：

(1)

(2)

(3)

式中，u和v分别表示x和y方向的水深平均速度；g表示重力加速度；B表示海底地形。在x和y方向上的非线性底摩擦分量可以表示为：

(4)

式中，n为曼宁系数，表示底边界的粗糙程度。

该模型利用了基于Godunov格式的有限体积方法进行数值离散，同时考虑了二阶修正项来减小数值震荡。自适应网格技术是该模型的一个特色，可以根据海啸波波高进行追踪判断是否对网格进行加密。该方法可以实现在海啸波未传播到的区域使用粗网格，减小计算量，提高计算效率，同时也可以用于网格嵌套，通过网格边界的传递实现海啸的越洋传播和局部高精度数值模拟相结合，该方法已得到Arcos和LeVeque的验证[20]。采用Okada有限断层模型计算得到海床底部变形[21]，将海底形变传递至海水表面，作为海啸波的初始条件，进一步利用浅水波模拟研究其传播特征，及对近岸岛礁的影响。

2.2 计算方案

本文首先以2011日本地震海啸为例，模拟研究其对凤凰岛的影响。进一步针对中国近海的马尼拉海沟和琉球海沟的潜在海啸源，分析其对凤凰岛的影响特征。最后结合环太平洋21个潜在极端震源，分析越洋海啸对近岸岛礁的影响。由于2011日本地震海啸和其他近海海啸源范围接近，因此采用一样的网格设置和地形分辨率。曼宁系数均采用0.024，库朗数设为0.75[12]。具体网格和地形分辨率参见表1。第一层包含日本地震海啸，马尼拉和琉球海沟潜在海啸的计算范围为5°～45°N，100°～160°E；第二层网格的范围为16.45°～19.20°N，108.75°～111.50°E；第三层网格的范围为18.05°～18.35°N，109.28°～109.60°E，如图1所示。同时布置了4个测点用于监测海啸波在岛礁附近引起的水位变化特征。越洋海啸的计算范围为50°S～70°N，100°E～60°W，第二层和第三层与近海海啸的计算范围相同。

表1 网格设置与地形分辨率

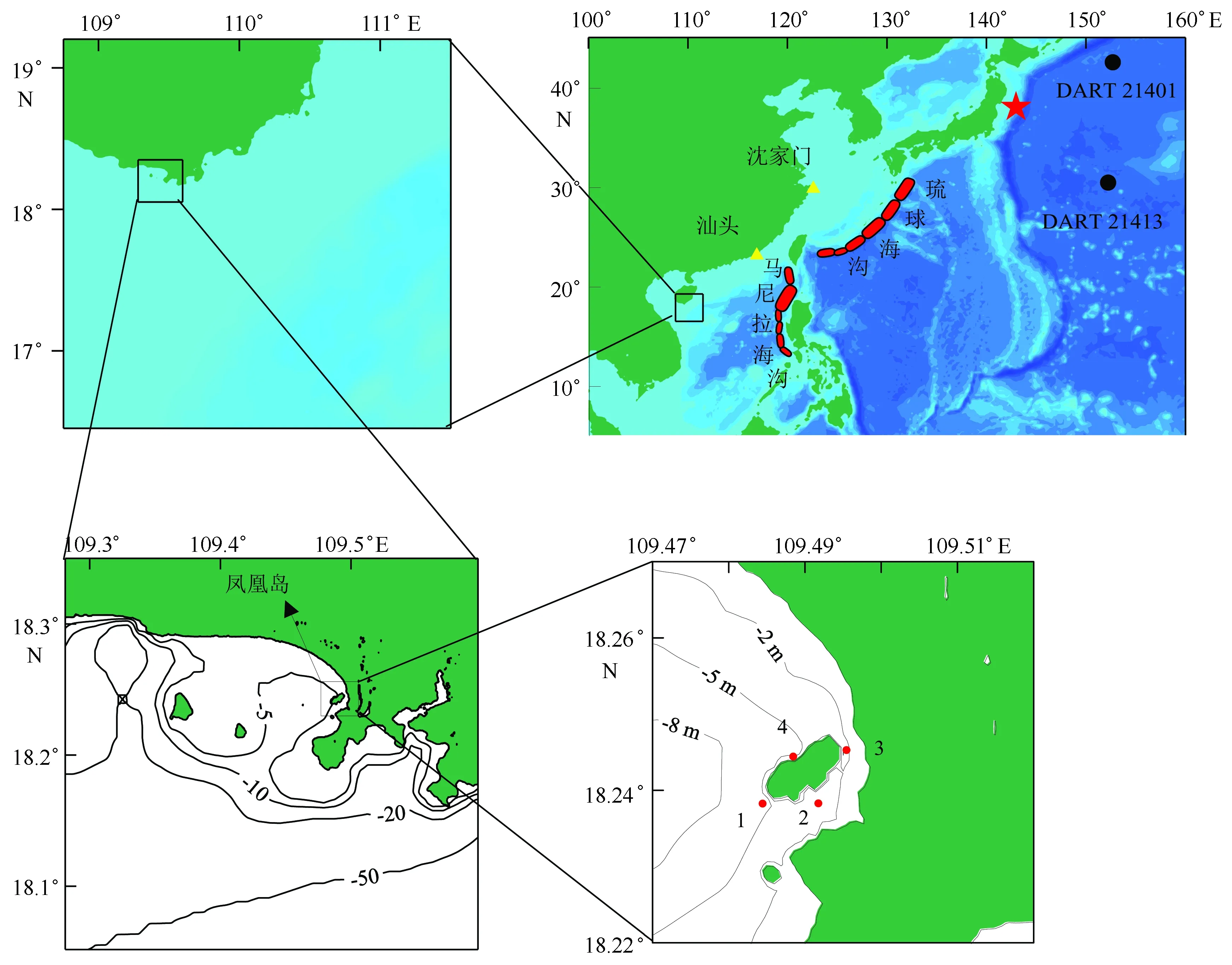
图1 近海海啸计算范围Fig.1 Computational domain of tsunami near Chinese coasts

3 2011日本海啸对凤凰岛的影响

发生于2011年3月11日的日本东北部地震海啸，是本世纪强度最大的一次地震海啸事件之一，尽管对日本当地的影响非常严重，但对中国的影响并不大。作为一次非常典型的地震海啸事件，结合海啸波实测数据，分析其对凤凰岛这样的近岸岛礁的影响具有重要的意义。此次地震的震中位于日本岛东北部(38.103°N，142.861°E)，图1中红色五角星所示。在地震发生后，许多学者结合地震观测数据对震源进行了细致的研究[22—24]。任智源和刘桦[25]，以及王培涛等[13]分别利用USGS和GCMT提供的初步震源机制解分析了此次海啸对中国沿海的影响。Shao等将整个地震断裂带划分为190个单元板块，他们利用27个P波的波形、23个SH波，53个表面波反演得到了每个单元板块的震源参数[26]。利用Okada模型根据单元板块的震源参数计算得到相关的地形响应变化，再将190个单元板块引起的海床变形进行线性叠加得到断裂带整个范围内海底地形响应的精细化形式。进一步利用非线性浅水波方程模拟计算海啸波的传播过程及对凤凰岛的影响。

图2首先给出了数值模拟结果和监测结果在DART浮标处和中国沿海潮位站的比较，以及凤凰岛周边监测点的波面时间序列及对应的功率谱密度。整体来看，模拟结果与实测结果比较吻合，包括海啸波首波的抵达时间和波高。在深海DART浮标处，根据UCSB震源模型计算的结果比实测值偏大，这与Grilli等的模拟结果和结论基本一致[4]。而在中国沿海的两个潮位站，计算结果与实测的海啸波波高接近，但抵达时间偏早18 min左右。海啸波在形成初期，首波的周期分别为28 min和64 min(DART_21401)，以及32 min和64 min(DART_221413)，到了中国沿海的沈家门，周期为37 min和57 min，而到了汕头周期为64 min。海啸波在抵达凤凰岛时的周期为68 min和128 min。这主要是因为海啸波在中国沿海的传播过程中，由于大陆架的和陆地边界的影响，所产生的边缘波和俘获波，使海啸在传播过程中周期发生变化，该现象在2010智利海啸中也得到了证实[27]。

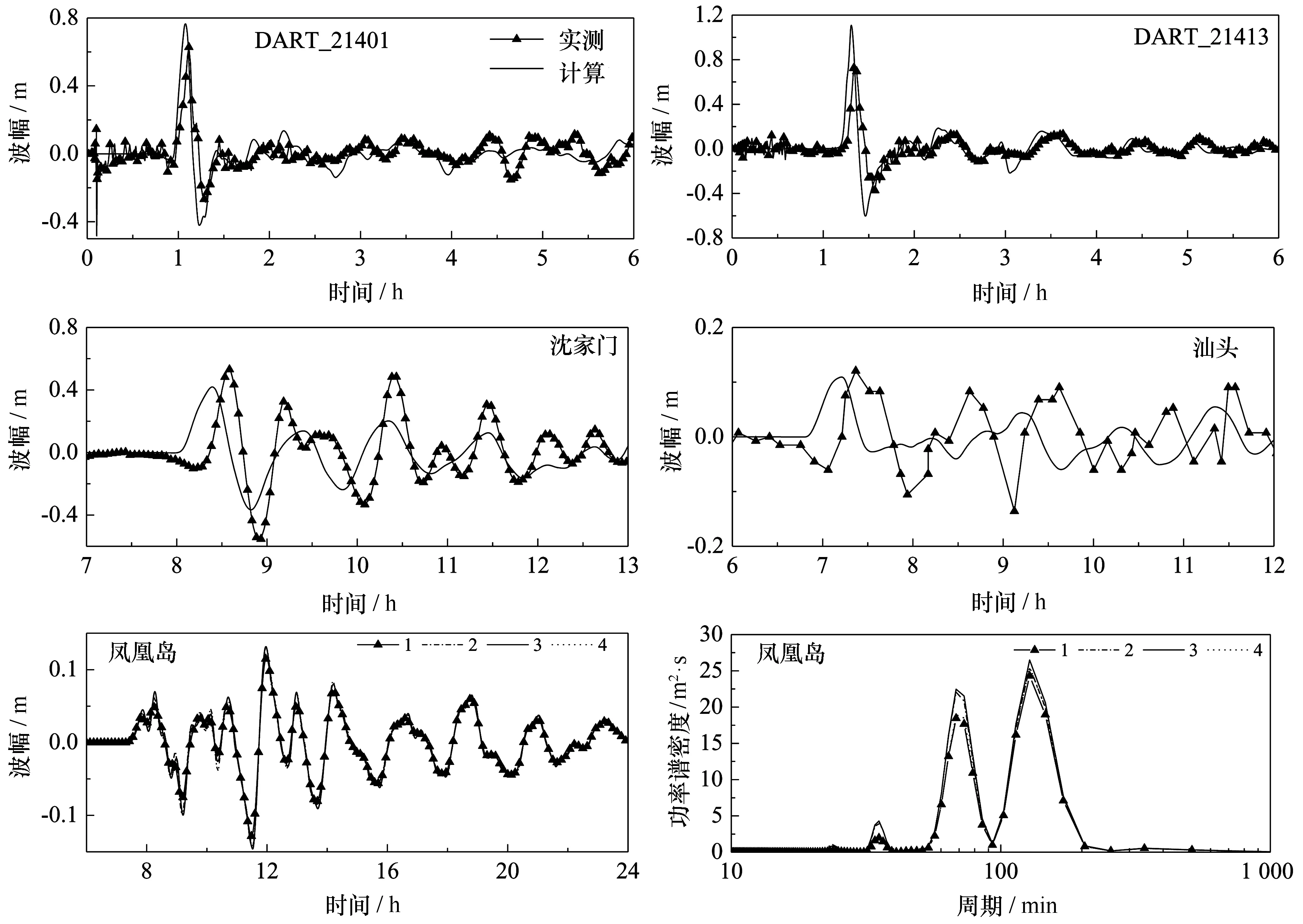
图2 2011日本海啸引发的监测位置波面时间序列Fig.2 Time series of surface elevation at measured locations induced by 2011 Japan tsunami

根据图2中海啸波在抵达凤凰岛后4个监测点的波面时间序列可以看出，尽管位于岛礁的不同位置，但抵达时间和波形基本一致。最大波幅并没有出现在首波，而是出现在第三个波。每个位置的最大波幅存在一定差异。如果将发生振幅最大的波峰和波谷组成一个海啸波，其波高分别为0.25 m、0.27 m、0.28 m、0.25 m。可以发现最大波高发生在岛礁背浪区的测点3，主要是由于海啸波在岛礁的绕射叠加和近岸反射的共同作用，使得测点3发生了较明显的海啸波放大效应。根据频谱分布可以看出测点3具有较大的能量密度。这里我们定义近岸岛礁对海啸波的放大指数为R，表示海啸波在岛礁处产生放大效应的强弱：

(5)

式中，hmax(i)表示波浪入射处的最大波高，即测点1的最大波高；hmax(i)表示岛礁背浪区的测点的最大波高，即测点3的最大波高。放大指数越大，表示海啸波在此处引起的放大效应越明显。日本地震海啸在三亚凤凰岛的放大指数为0.12。

图3给出了2011日本地震海啸在全场和凤凰岛附近的最大波幅分布。受地震位置和地形的影响，海啸的总能量主要释放在太平洋中，除了对东海存在一定影响，对中国沿海整体影响偏小。海啸在到达三亚后，在大东海产生比较明显的能量聚集，而对凤凰岛的影响较小。

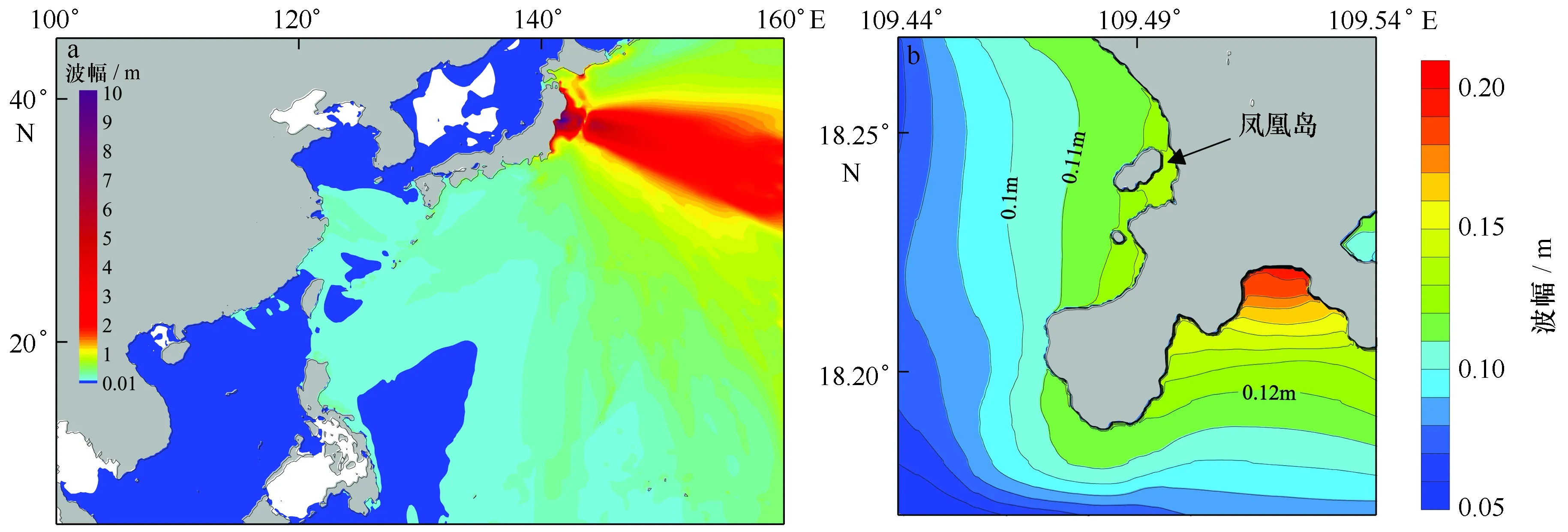
图3 2011日本地震海啸最大波幅分布(a为全场结果；b为凤凰岛附近的最大波幅分布)Fig.3 Distribution of maximum wave amplitude of 2011 Japan tsunami (a.distribution in the whole computational domain; b.results near Phoenix Island)

4 潜在海啸对凤凰岛的影响研究

在上一节中，针对2011日本地震海啸对凤凰岛的数值研究的基础上，取得了验证结果，并初步分析了此次海啸事件对凤凰岛的影响及其放大效应。在本节中，本文将利用数值模型对中国近海的马尼拉海沟和琉球海沟潜在地震海啸，及环太平洋的21个越洋海啸源进行模拟计算，分析其对凤凰岛的影响及海啸波的波浪特征。

4.1 马尼拉海沟潜在海啸

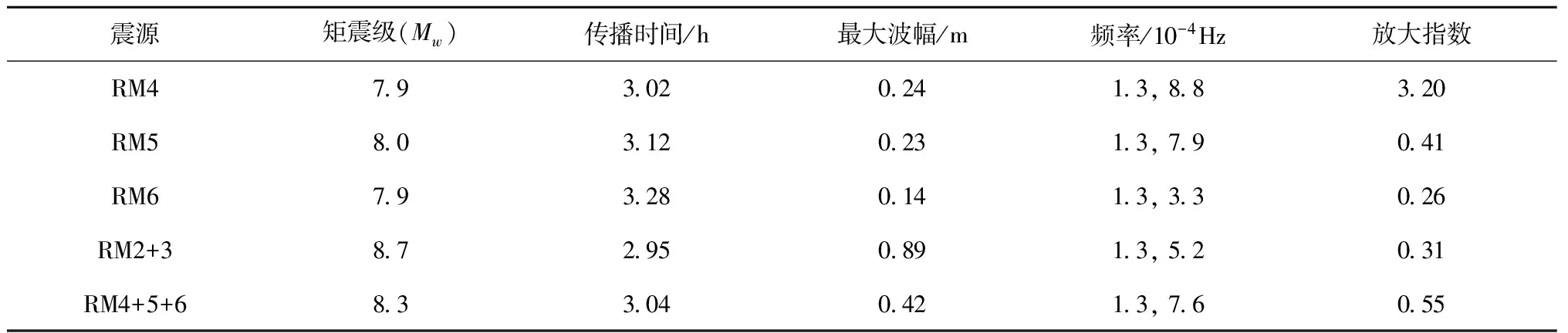
根据板块构造特征将马尼拉海沟划分为6个断裂带，如图1所示，由北向南分别记为RM1～RM6，以及两种组合形式。根据每一个板块的震源参数，模拟得到每个板块运动所激发的海啸对凤凰岛的影响。表2总结了马尼拉海沟潜在震源所引发的海啸抵达凤凰岛之后的海啸基本信息和波浪特征，包括地震矩震级、海啸传播时间、最大海啸波波幅、频率，以及放大效应指数。总体而言，马尼拉海沟所引发的海啸抵达凤凰岛需要3 h左右，RM2所引起的最大波幅超过了90 cm。除了RM6板块，其他情景的海啸波抵达凤凰岛后除了具有1.3×10-4Hz的低频波，还具有3.3×10-4～8.8×10-4Hz的高频波，从而使得放大效应比较显著。

表2 马尼拉海沟潜在海啸对凤凰岛影响的海啸波特征

续表2

图4为马尼拉海沟RM2震源激发的海啸引起的全场和凤凰岛附近的最大波幅分布。总体来看，马尼拉海沟所激发的海啸主要对南海范围内产生较大影响，包括了台湾、福建、广东、海南等中国省份，以及菲律宾、马来西亚、越南等南海周边国家。海啸不仅在大东海发生了明显的能量聚集效应，而且在对凤凰岛的影响过程中也产生了较大的梯度变化，最大波幅从0.6 m增大到0.9 m。

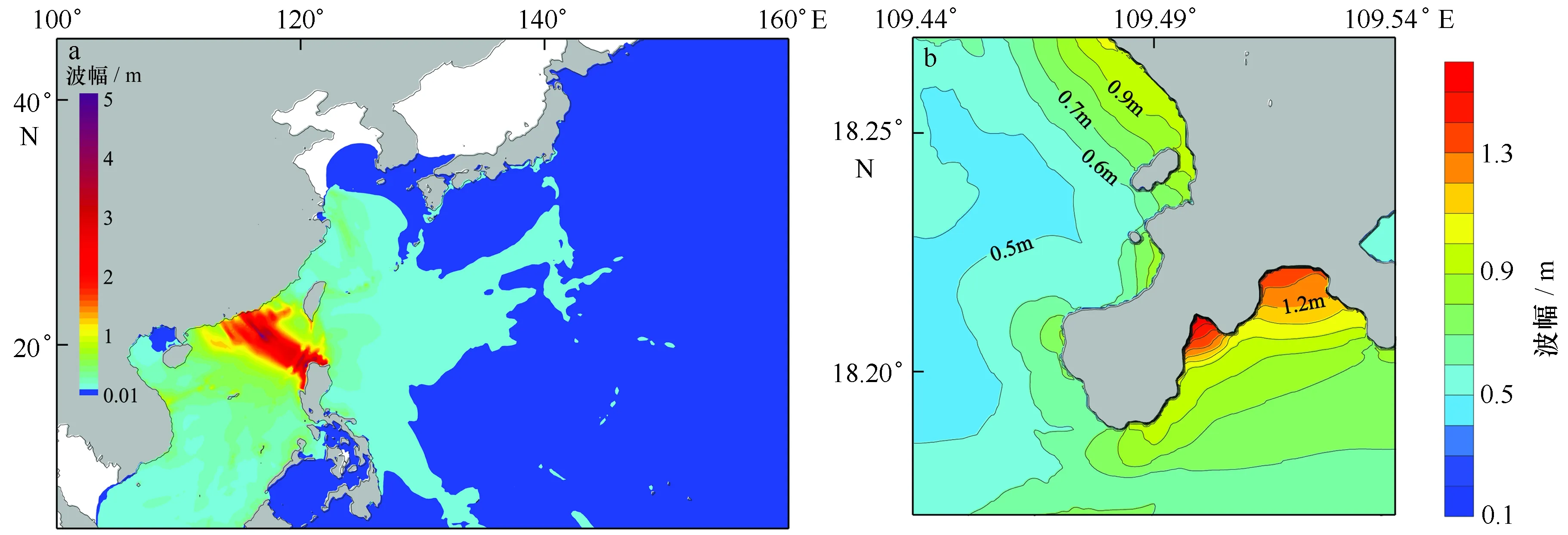
图4 马尼拉海沟RM2震源引起的海啸最大波幅分布(a为全场结果；b为凤凰岛附近的最大波幅分布)Fig.4 Distribution of maximum wave amplitude of RM2 fault (a. distribution in the whole computational domain; b. results near Phoenix Island)

图5给出了凤凰岛外海(测点1)和近岸(测点3)的波面时间序列及功率谱密度图。海啸波首波的波形存在明显差异，岛礁内侧海啸波明显变强。根据功率谱密度可以看出，测点3除了具有较大的能量密度，还产生了的高频波，这也是放大效应较强的原因。

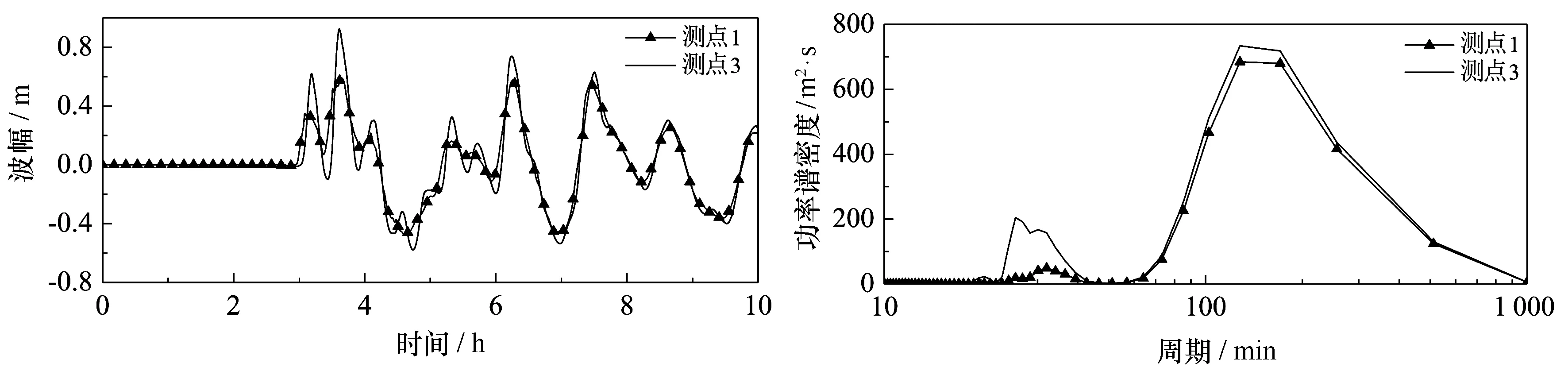
图5 马尼拉海沟RM2震源引起的凤凰岛附近测点波面时间序列及功率谱密度图Fig.5 Time series of surface elevation triggered by RM2 fault near Phoenix Island， along with respective spectra

4.2 琉球海沟潜在海啸

根据板块构造特征同样将琉球海沟划分为6个断裂带，如图1所示，由北向南分别记为RL1～RL6，以及一种组合形式(RL5+6)。根据每一个板块的震源参数，模拟得到每个板块运动所激发的海啸对凤凰岛的影响。表3总结了琉球海沟潜在震源所引发的海啸抵达凤凰岛之后的海啸基本信息和波浪特征。总体而言，琉球海沟所引发的海啸抵达凤凰岛需要4～5.39 h不等，最大波幅整体偏小，在5～20 cm之间。海啸波抵达凤凰岛后的波浪频率在1.3×10-4Hz。放大指数偏小，放大效应并不显著。

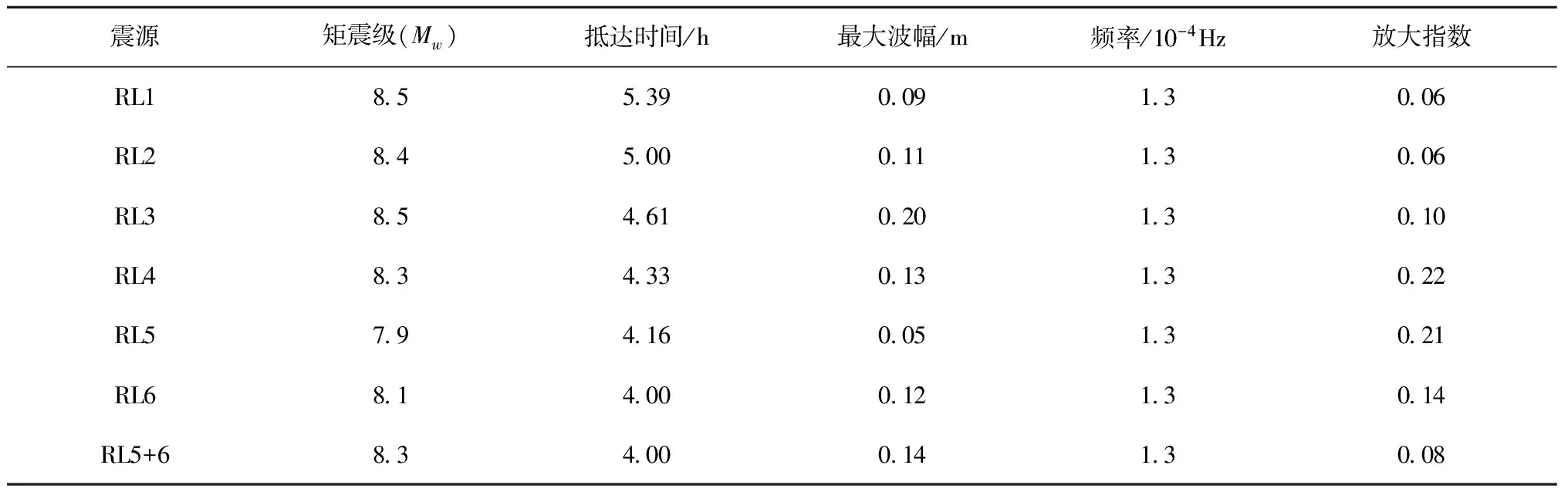
表3 琉球海沟潜在海啸对凤凰岛影响的海啸波特征

图6为琉球海沟RL3震源激发的海啸引起的全场和凤凰岛附近的最大波幅分布。琉球海沟所激发的海啸主要对东海和黄海产生较大影响，包括了我国东南沿海等省份。海啸在三亚半岛两侧的大东海和三亚港均发生了明显的能量聚集效应。在对凤凰岛的影响过程中海啸波梯度变化较小，放大效应不强。图7给出了凤凰岛附近测点1和测点3的波面时间序列及功率谱密度图。除了测点3波幅和能量密度稍大，海啸波波形基本一致。

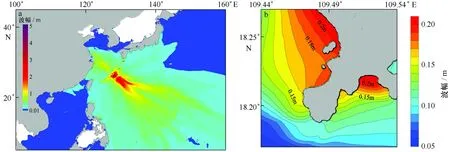
图6 琉球海沟RL3震源引发的海啸最大波幅分布(a为全场结果；b为凤凰岛附近的最大波幅分布)Fig.6 Distribution of maximum wave amplitude of RL3 fault (a.distribution in the whole computational domain; b.results near Phoenix Island)

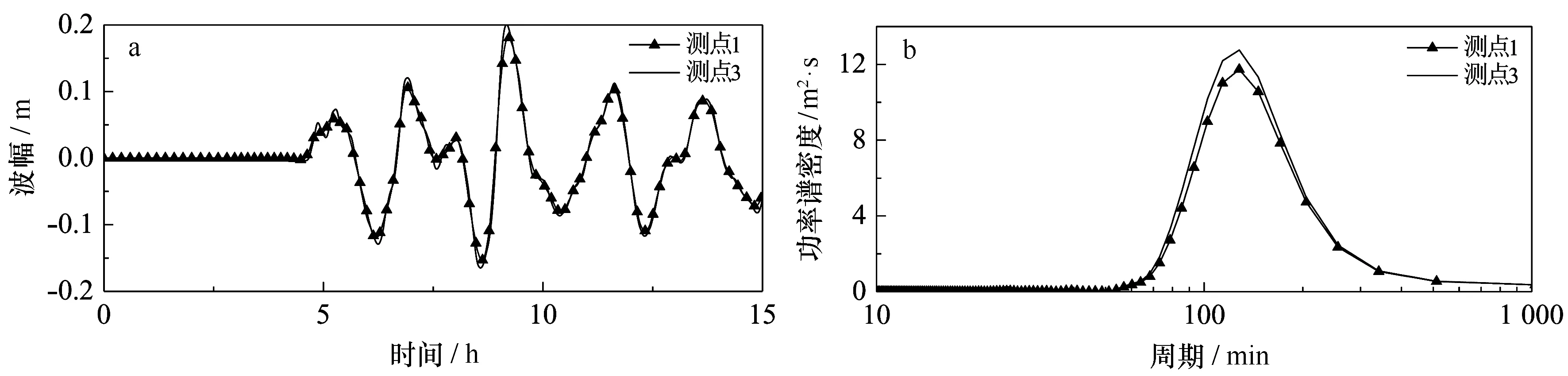
图7 琉球海沟RL3震源引起的凤凰岛附近测点波面时间序列(a)及功率谱密度(b)Fig.7 Time series of surface elevation triggered by RL3 fault near Phoenix Island， along with respective spectra

4.3 越洋海啸

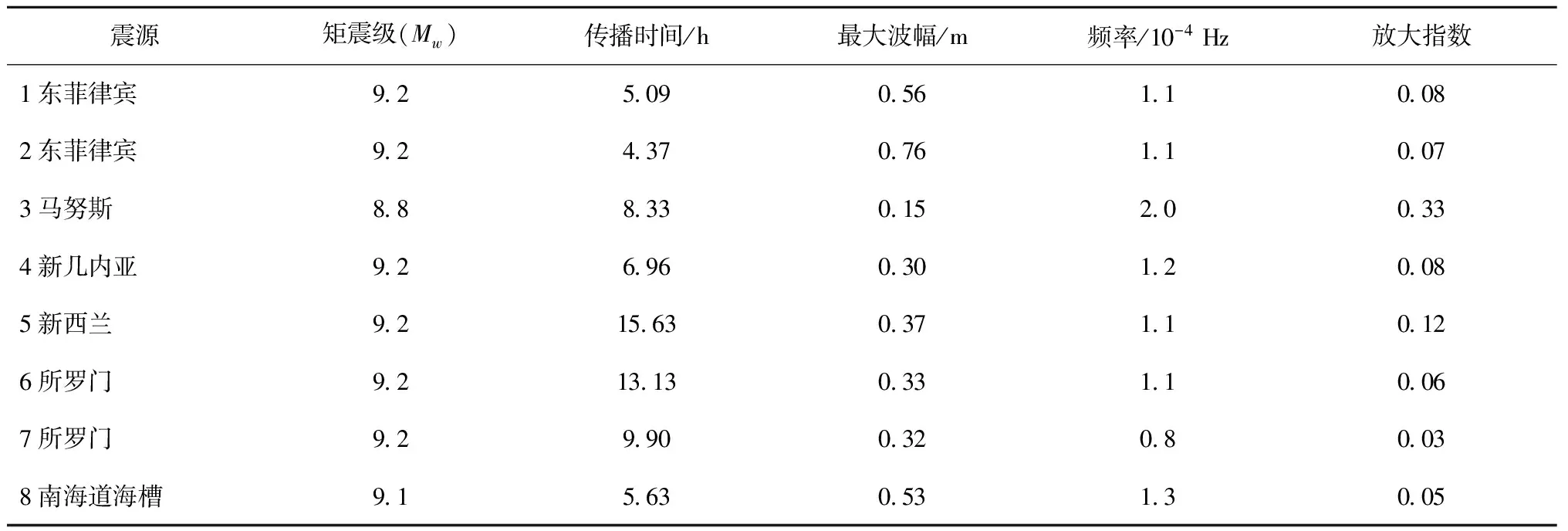
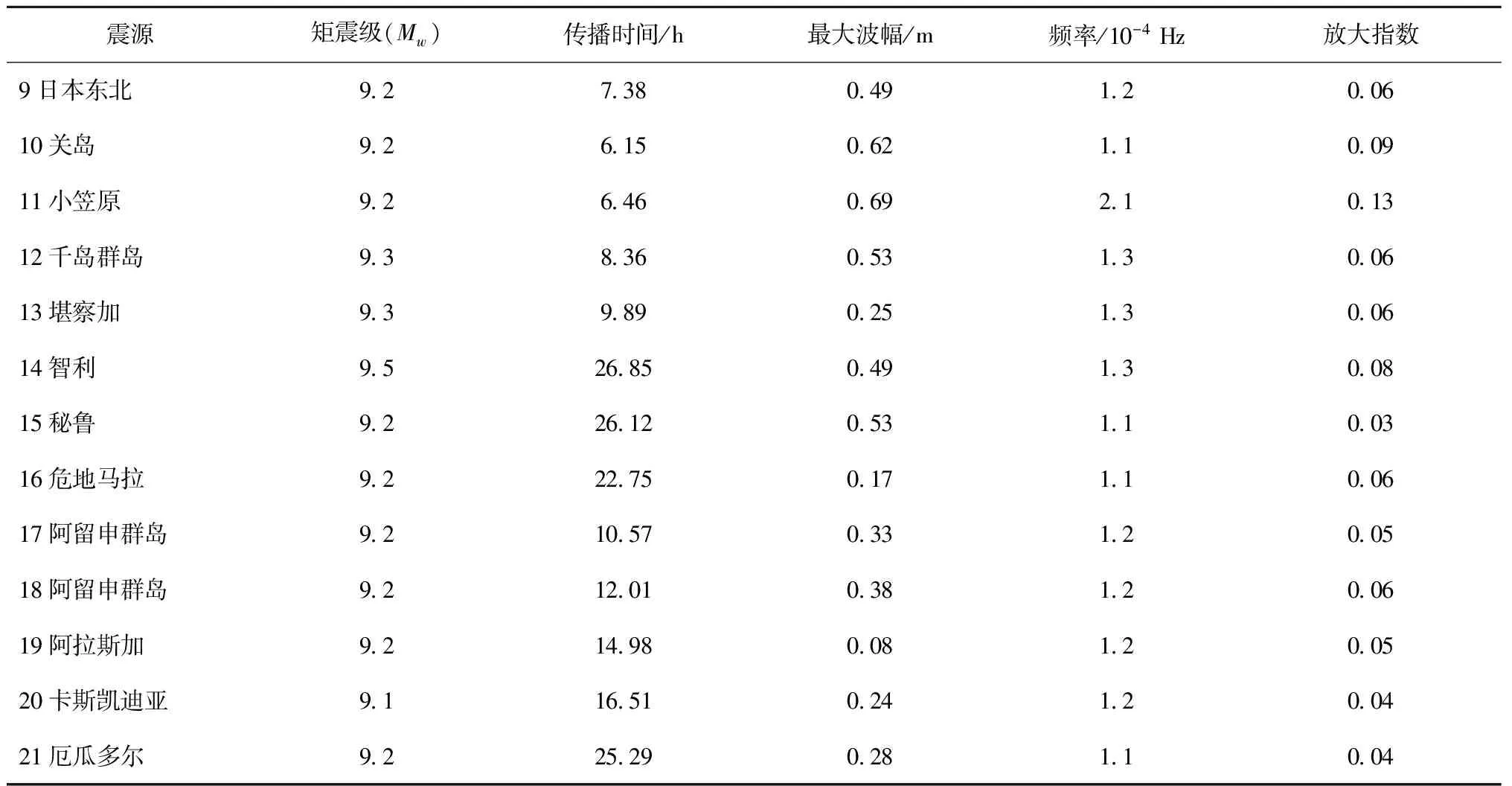
根据太平洋板块的构造特征及板块边缘的地质活动情况，结合历史上的地震数据，构造了21个环太平洋分布的特大地震海啸源，分布情况如图8所示。利用数值模型及高精度嵌套网格，计算模拟了海啸越洋传播及对凤凰岛的影响。表4总结了21个极端越洋海啸抵达凤凰岛之后的海啸基本信息和波浪特征。由于传播距离的不同，海啸的传播时间从4.37 h到约27 h不等。根据震中位置与凤凰岛的直线距离，图9给出了越洋海啸传播时间与距离的关系。总的来说，传播时间与距离接近线性关系，但由于地形和水深的影响，海啸并非沿直线传播，且传播速度也不是保持不变。根据线性关系发现海啸在太平洋传播的平均速度为713 km/h，相当于在4 000 m平均水深的海水中传播，接近太平洋的平均水深。

图8 环太平洋21个潜在极端海啸源位置分布Fig.8 Locations of 21 extreme tsunami sources around Pacific

震源矩震级(Mw)传播时间/h最大波幅/m频率/10-4Hz放大指数1东菲律宾92509056110082东菲律宾92437076110073马努斯88833015200334新几内亚92696030120085新西兰921563037110126所罗门921313033110067所罗门92990032080038南海道海槽9156305313005

续表4

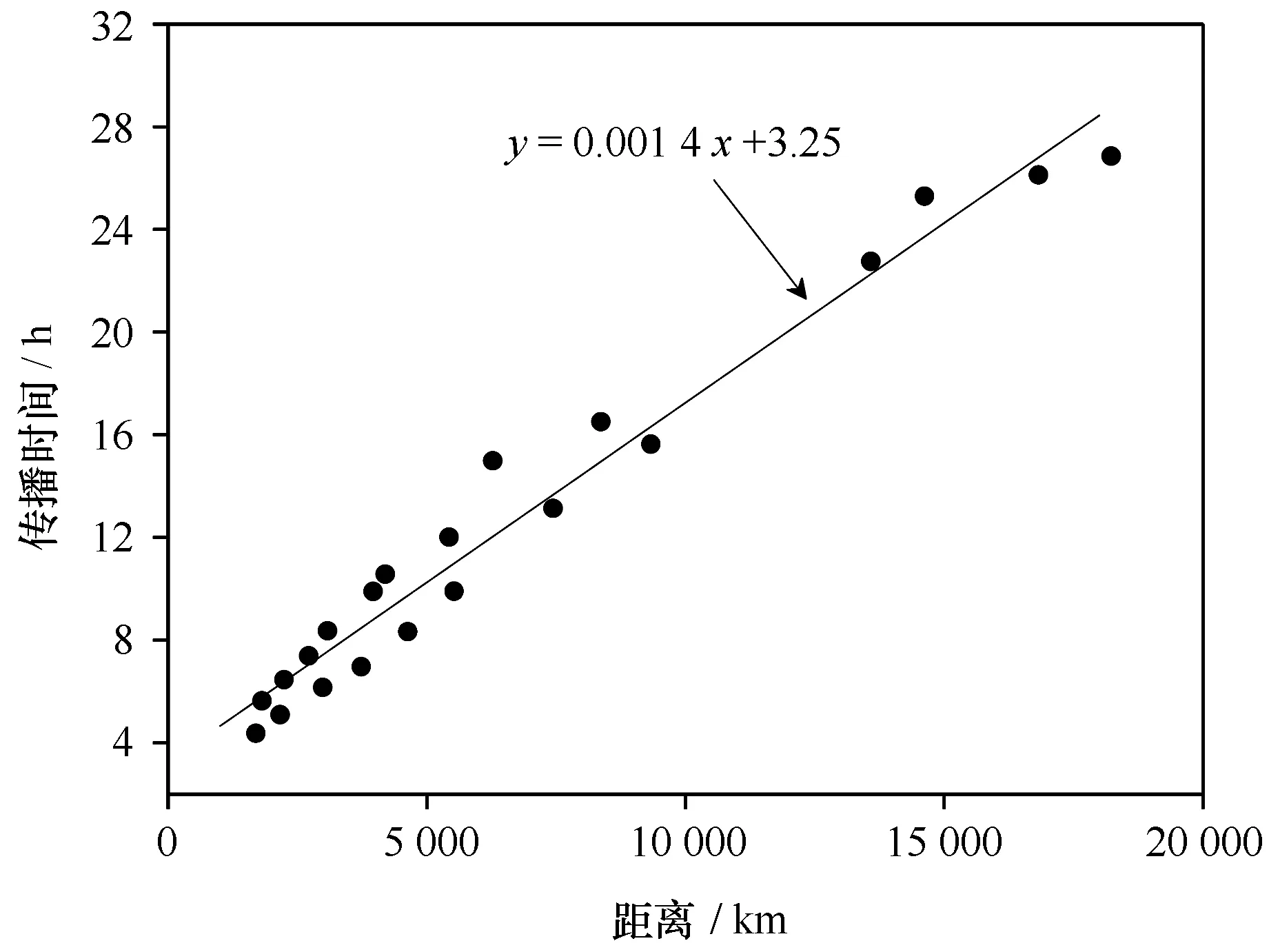
图9 越洋海啸传播时间与距离的关系Fig.9 Relationship of travel time and propagation distance for trans-Pacific tsunami

越洋海啸在凤凰岛附近水域引起的最大波幅从0.08 m到0.76 m不等。这与震中位置、断裂带走向等都有一定关系。如东菲律宾2号震源距离凤凰岛最近，因此产生的波幅最大。而阿拉斯加震源所激发的海啸主要向赤道方向传播，因而对凤凰岛的影响很小。尽管地处南美西海岸的秘鲁和智利震源所产生海啸需要横跨整个太平洋才能抵达三亚凤凰岛，但凤凰岛附近的海啸波也达到了0.5 m左右，因此需要重视越洋海啸的潜在威胁。越洋海啸传播至凤凰岛附近的海啸波以低频为主，介于0.8×10-4～2.1×10-4Hz。除了马努斯之外，海啸波在岛礁附近的放大效应偏小，均小于0.15。

由于智利西海岸地震频繁，近几年来分别于2010年、2014年、2015年发生了超过8.0级以上的地震并引发了整个太平洋范围内的海啸波动，相应的海啸越洋传播特性已得到较为全面的阐述。因此本文主要选了秘鲁震源引发的海啸进行分析。图10为秘鲁潜在特大海啸引起的整个太平洋及凤凰岛附近的最大波幅分布。考虑岸线的影响，震源的走向角设为316°，海啸的能量主要释放在南太平洋，而对北太平洋影响相对较小。但该场景的海啸波依然对凤凰岛造成较大影响，附近最大波幅超过0.5 m(图11)，因此这类越洋海啸可能造成的威胁依然不容忽视。

图10 秘鲁潜在特大海啸引起的最大波幅分布(a为全场结果；b为凤凰岛附近的最大波幅分布)Fig.10 Distribution of maximum wave amplitude induced by source of Peru (a.distribution in the whole computationaldomain; b.results near Phoenix Island)

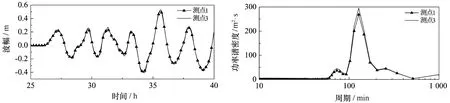
图11 秘鲁潜在特大海啸引起的凤凰岛附近测点波面时间序列及功率谱密度图Fig.11 Time series of surface elevation triggered by extreme tsunami source of Peru near Phoenix Island， along with respective spectra

5 讨论与分析

本文在基于分析2011日本地震海啸对凤凰岛影响的基础上，针对多个潜在海啸源，探索分析海啸波对近岸人工岛礁的影响特征和放大效应。根据数值模拟结果，2011日本地震海啸对凤凰岛的影响相对较小，最大波幅达到了10 cm。由于受到地形的影响，海啸的能量主要释放在太平洋，对中国沿海的影响并不大。在漫长的传播过程中，受到陆地边界和大陆架的影响，到达凤凰岛之后的波幅就很小，但海啸波的周期受边缘波和俘获波的影响变化较大。而其相对波高(波幅与水深之比)也从开始的1.2×10-4(DART21413)变为0.026，海啸波的非线性效应逐渐增强。这也说明了在马尼拉和琉球潜在海啸的计算中，组合板块产生的海啸的最大波幅并不等于单个板块激发的海啸波。

图12 不同震源所引起的放大指数与波浪频率的关系Fig.12 Relationship of amplification index and wave frequency for different earthquake sources

图12综合了不同地区的震源引发的海啸在凤凰岛的放大指数与波浪频率的关系，其中马尼拉海沟潜在海啸的频率取高频。相对于其他地区的潜在地震海啸，马尼拉海沟潜在海啸更容易在凤凰岛产生较强的放大效应，同时伴有高频的海啸波。这主要是由于三亚东南半岛的影响，形成了一定的庇护区，琉球海沟和环太平洋的潜在海啸波传播至半岛附近经历了绕射作用。而马尼拉海沟的潜在海啸可以在形成之后，可以直接袭击凤凰岛，因而产生较明显的放大效应。

根据Stefanakis等[11]的结论，当海啸波的波长与岛礁的半径相等时，会产生最强的爬高放大效应。但凤凰岛的量级为O (1 km)。根据波浪传播的色散关系，

(6)

式中，ω为频率；g为重力系数；k表示波数(k=2π/L)，L为波长；d表示水深。由于琉球海沟潜在海啸以及环太平洋的潜在越洋海啸在传播过程中受地形和陆地边界影响较大，周期会发生改变；而马尼拉海沟所产生的海啸可以直接传播至凤凰岛，周期受影响较小。以马尼拉海沟RM1为例。初始波长L0为79 km，水深d0为3 000 m。根据色散关系式计算得到海啸传播至凤凰岛附近水深10 m处的波长为4.6 km。对比Stefanakis等[11]的论文中的图14，爬高放大系数与波长岛礁尺度比的关系，发现本文该算例中波长岛礁尺度比为4.6，放大系数接近爬高放大系数。如果针对真实的近岸岛礁，水深、坡度等地形因素，以及海啸波的波浪特征会对放大效应产生一定影响。

6 结论

本文重点研究海啸波对近岸岛礁的影响规律，选取了三亚市凤凰岛作为研究对象。依据非线性浅水波数值模型和高精度嵌套网格，以2011日本地震海啸为例，结合实测数据分析海啸波对中国沿海及对凤凰岛的影响特征。针对中国近海的马尼拉和琉球海沟潜在震源，以及环太平洋的21个潜在特大地震源，系统评估分析了潜在海啸对凤凰岛的影响规律。马尼拉海沟和琉球海沟的潜在海啸抵达凤凰岛需要3 h左右及4 h以上。马尼拉海沟8.6级的地震海啸可以使凤凰岛附近产生最大波幅接近1 m的海啸波。而琉球海沟对凤凰岛的影响相对较小，根据额外计算的琉球海沟RL3板块发生9.0级地震，发现最大波幅为0.42 m。根据21个环太平洋的特大地震海啸模拟结果发现，海啸的传播时间根据传播距离从4.37 h到27 h不等。不同潜在震源的位置及断裂带特征都对结果有一定影响。即使对于需要横跨太平洋的秘鲁和智利的潜在特大海啸，依然可以在凤凰岛附近引起0.5 m左右的海啸波，因此这些潜在震源可能引起的海啸风险不容忽视。本文在岛礁附近选取的测点水深在2～5 m左右，海啸在到达岛礁附近之后的爬高、淹没、对岛礁结构物的水动力荷载，以及可能引起的共振现象需要在进一步的工作中深入研究。

根据岛礁附近不同位置的波高及相应的功率谱密度，本文初步探讨了近岸岛礁对海啸波的放大效应。对于真实的近岸岛礁，往往地形条件复杂。而凤凰岛附近的半岛，使传播过来的海啸波发生了绕射，对岛礁形成了一定保护作用，使得不容易发生放大效应。而马尼拉海沟所激发的海啸，可以直接抵达凤凰岛，更容易发生较强的放大效应。这也说明了马尼拉海沟是更为值得关注的海啸源。因此，评估分析马尼拉海沟潜在极端海啸威胁，发展快速、有效的海啸预警方法有助于防范和减少海啸所产生的自然灾害。

致谢:感谢上海交通大学刘桦教授的指导。与爱尔兰都柏林大学的Frederic Dias教授的讨论丰富了本文的研究内容。

[1] Grilli S T， Ioualalen M， Asavanant J， et al. Source constraints and model simulation of the December 26， 2004， Indian Ocean tsunami[J]. Journal of Waterway， Port， Coastal， and Ocean Engineering， 2007， 133(6): 414-428．

[2] Fujii Y， Satake K. Tsunami source of the 2004 Sumatra-Andaman earthquake inferred from tide gauge and satellite data[J]. Bulletin of the Seismological Society of America， 2007， 97(1A): S192-S207．

[3] Popinet S. Adaptive modelling of long-distance wave propagation and fine-scale flooding during the Tohoku tsunami[J]. Nature Hazards Earth System Sciences， 2012， 12(4): 1213-1227．

[4] Grilli S T， Harris J C， Bakhsh T S T， et al. Numerical simulation of the 2011 Tohoku tsunami based on a new transient FEM co-seismic source: Comparison to far-and near-field observations[J]. Pure and Applied Geophysics， 2013， 170(6/8): 1333-1359．

[5] 刘桦， 赵曦， 王本龙， 等. 海啸数值模拟与南海海啸预警方法[J]. 力学季刊， 2015， 36(3): 351-369．

Liu Hua， Zhao Xi， Wang Benlong， et al. Numerical simulation of tsunami and tsunami warning methods for South China Sea region[J]. Chinese Quarterly of Mechanics， 2015， 36(3): 351-369．

[6] Yeh H， Imamura F， Synolakis C， et al. The Flores island tsunamis[J]. EOS， Transactions American Geophysical Union， 1993， 74(33): 369-373．

[7] Kim K O， Kim D C， Choi B H， et al. The role of diffraction effects in extreme run-up inundation at Okushiri Island due to 1993 tsunami[J]. Natural Hazards and Earth System Sciences， 2015， 15(4): 747-755．

[8] 刘思， 柳淑学， 李金宣. 岛礁地形上二维波浪传播的数值模拟[J]. 港工技术， 2015， 52(5): 1-5．

Liu Si， Liu Shuxue， Li Jinxuan. Numerical simulation of two-dimensional wave propagation by reef island[J]. Port Engineering Technology， 2015， 52(5): 1-5．

[9] 方亚冰， 柳淑学， 李金宣， 等. 基于缓坡方程在岛礁地形上波浪破碎的模拟研究[J]. 水道港口， 2015， 36(4): 290-296．

Fang Yabing， Liu Shuxue， Li Jinxuan， et al. Simulation of wave breaking on the reefs terrain using mild slope equation[J]. Journal of Waterway and Harbor， 2015， 36(4): 290-296．

[10] Berger M J， George D L， LeVeque R J， et al. The GeoClaw software for depth-averaged flows with adaptive refinement[J]. Advances in Water Resources， 2011， 34(9): 1195-1206．

[11] Stefanakis T S， Contal E， Vayatis N， et al. Can small islands protect nearby coasts from tsunamis？ An active experimental design approach[J]. Proceedings of The Royal Society A， 2014， 470(2172): 20140575．

[12] Ren Z， Wang B， Fan T， et al. Numerical analysis of impacts of 2011 Japan Tohoku tsunami on China Coast[J]. Journal of Hydrodynamics， Ser. B， 2013， 25(4): 580-590．

[13] 王培涛， 于福江， 赵联大， 等. 2011 年 3 月 11 日日本地震海啸越洋传播及对中国影响的数值分析[J]. 地球物理学报， 2012， 55(9): 3088-3096．

Wang Peitao， Yu Fujiang， Zhao Lianda， et al. Numerical analysis of tsunami propagating generated by the JapanMw9.0 earthquake on Mar. 11 in 2011 and its impact on China coasts[J]. Chinese Journal of Geophysics， 2012， 55(9): 3088-3096．

[14] Glimsdal S， Pedersen G K， Harbitz C B， et al. Dispersion of tsunamis: does it really matter[J]. Nature Hazards Earth System Sciences， 2013， 13(6): 1507-1526．

[15] Ren Z Y， Zhao X， Liu H. Dispersion effects on tsunami propagation in South China Sea[J]. Journal of Earthquake and Tsunami， 2015， 9(5): 1540001．

[16] Kirby J T， Shi F， Tehranirad B， et al. Dispersive tsunami waves in the ocean: Model equations and sensitivity to dispersion and Coriolis effects[J]. Ocean Modelling， 2013， 62: 39-55．

[17] Liu Y， Shi Y， Yuen D A， et al. Comparison of linear and nonlinear shallow wave water equations applied to tsunami waves over the China Sea[J]. Acta Geotechnica， 2009， 4(2): 129-137．

[18] 王培涛， 于福江， 范婷婷， 等. 海啸波传播的线性和非线性特性及近海陆架效应影响的数值研究[J]. 海洋学报， 2014， 36(5): 18-29．

Wang Peitao， Yu Fujiang， Fan Tingting， et al. Numerical study on the linear/ nonlinear characteristics and the impacts of continental shelf effects of the tsunami waves propagating[J]. Haiyang Xuebao， 2014， 36(5): 18-29．

[19] LeVeque R J， George D L， Berger M J. Tsunami modelling with adaptively refined finite volume methods[J]. Acta Numerica， 2011， 20: 211-289．

[20] Arcos M E M， LeVeque R J. Validating velocities in the GeoClaw tsunami model using observations near Hawaii from the 2011 Tohoku Tsunami[J]. Pure and Applied Geophysics， 2015， 172(3/4):849-867．

[21] Okada Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America， 1985， 75(4): 1135-1154．

[22] Hayes G P. Rapid source characterization of the 2011Mw9.0 off the Pacific coast of Tohoku Earthquake[J]. Earth， Planets and Space， 2011， 63(7): 529-534．

[23] Fujii Y， Satake K， Sakai S， et al. Tsunami source of the 2011 off the Pacific coast of Tohoku Earthquake[J]. Earth， Planets and Space， 2011， 63(7): 815-820．

[24] Saito T， Ito Y， Inazu D， et al. Tsunami source of the 2011 Tohoku-Oki earthquake， Japan: Inversion analysis based on dispersive tsunami simulations[J]. Geophysical Research Letters， 2011， 38(7):LOOG19．

[25] 任智源， 刘桦. 日本东部地震海啸对我国沿海地区影响的数值分析[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰 110 周年纪念大会文集 (下册). 2012．

Ren Zhiyuan， Liu Hua. Numerical analysis of 2011 Tohoku tsunami and its impact on China Coast[C]//Proceeding of the 11th National Congress on Hydrodynamics & 24th National Conference on Hydrodynamics and Commemoration of the 110th Anniversary of Zhou Pei-yuan’s Birth， 2012．

[26] Shao G， Li X， Ji C， et al. Focal mechanism and slip history of the 2011 Mw 9.1 off the Pacific coast of Tohoku Earthquake， constrained with teleseismic body and surface waves[J]. Earth， Planets and Space， 2011， 63(7): 559-564．

[27] Yamazaki Y， Cheung K F. Shelf resonance and impact of near-field tsunami generated by the 2010 Chile earthquake[J]. Geophysical Research Letters， 2011， 38(12):564-570．

Numerical study of tsunami impact on coastal reef

Ren Zhiyuan1，2， Zhao Xi3， Shan Di1，2， Wang Peitao1，2

(1.NationalMarineandEnvironmentalForecastCenter，Beijing100081，China; 2.NationalTsunamiWarningCenter，StateOceanicAdministration,Beijing100081，China；3.DepartmentofEngineeringMechanics，ShanghaiJiaoTongUniversity，Shanghai200240，China)

In this study， tsunami generation and propagation model involved trans-Pacific (China’s offshore) -local-coastal reef has been established， based on Okada model， nonlinear shallow water equations， and coupled grid with high resolution. The Phoenix Island in Sanya City is selected as research subject. Firstly， the simulation of 2011 Japan Tohoku tsunami has been carried out， and the characteristics of tsunami propagation along the continental shelf of Chinese coasts and the impacts on Phoenix Island are presented， combined with real-time measurements. The impacts of tsunami source along Manila Trench， Ryukyu Trench， and 21 extreme sources around Pacific on Phoenix Island are discussed. According to characteristics of tsunami wave near the Phoenix Island， the amplification effect of tsunami wave near coastal reef is discussed based on Fouriers analysis. It turns out that relatively moderate tsunami near Chinese coasts and extreme trans-Pacific tsunami will have some impacts on Phoenix Island， which may induce tsunami of maximum amplitude reached 1 m. The travel time ranges from 3 h to 27 h. Due to the impact of southeast peninsula Sanya， tsunami from Ryukyu Trench and trans-Pacific tsunami will generate less amplification effect than Manila Trench due to wave diffraction， whose frequency are in the range of 0.8×10-4-2×10-4Hz. The tsunami from Manila Trench may produce obvious amplification effect， and require more attention．

tsunami wave; coastal reef; numerical simulation; Phoenix Island; amplification effect

2016-03-18；

2016-09-26。

国家自然科学基金(11202130)；国家海洋公益性行业科研专项项目(201405026)；国家重点研发计划(2016YFC1401500)；上海交通大学海洋工程国家重点实验室开放课题(1604)；留学人员科技活动项目择优资助。

任智源(1986—)，男，陕西省西安市人，博士，主要从事水动力学的研究。E-mail:zhyren@foxmail.com

O352

A

0253-4193(2017)03-0001-13