风机叶片试验台疲劳加载振动干涉研究

乐韵斐，王 庚

（同济大学机械与能源工程学院，上海201804）

根据IEC61400–23标准，对于新研制或者工艺做出重大更改后的风机叶片，均需做叶片全尺寸结构测试，验证叶片的静强度和疲劳强度，并为刚度检验以及结构优化设计等提供必要的数据。风机叶片试验台作为风机叶片测试的基础平台，对风机叶片全尺寸结构检测等领域的研究至关重要。随着风力发电机组的迅速发展，风机测试验证的难度也在逐步提高，并带来了一些新问题，如为提高试验台利用率和叶片测试效率，设计风机叶片试验台可以两侧同时加载，这时就要考虑两侧叶片疲劳振动时的干涉问题。

本文建立了风机叶片试验台基座和两个叶片模型，并分析了叶片和基座的固有频率；进而详细研究了基座的刚度、两侧叶片固有频率差异对叶片疲劳加载振动干涉的影响，从而提高基座的刚度，规范试验台两边加载叶片，降低风机叶片试验台疲劳加载振动干涉的影响。

1 模态和谐响应分析

模态分析是最基本的动力学分析，也是其他动力学分析的基础。模态分析是计算结构振动特性（固有频率和振型）的数值计算，实际上就是进行特征值和特征向量的求解。无阻尼模态分析动力学问题的运动方程如式（1）所示。

（M）（x″）+（K）（x）=0 （1）

式中，[M]是质量矩阵；[K]是刚度矩阵；[x]是位移矢量。

结构的自由振动为简谐振动，即位移为圆频率正弦函数：

将（2）式带入（1）式得结构特征方程：

（（K）-ω2（M））（x）=0（3）

谐响应分析也称为频率响应分析，用于确定结构在已知频率和幅值的正弦载荷作用下的稳态响应，从而分析共振，指导设计人员避免结构发生共振[2]。由经典力学理论可以得到谐响应分析通用方程：

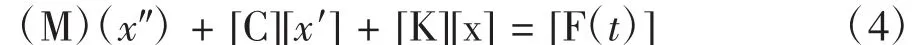
其中，[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；[x]是位移矢量；[F（t）]为力矢量，在谐响应中，[F（t）]=F0cos（ωt）.

2 风机叶片试验台模型

风机叶片试验台模型由横筒体、竖筒体、法兰及两边叶片组成。做双侧疲劳试验时，两边叶片通过叶根根部的一周螺栓与横筒体两边的法兰连接。整个试验台模型如图1所示。

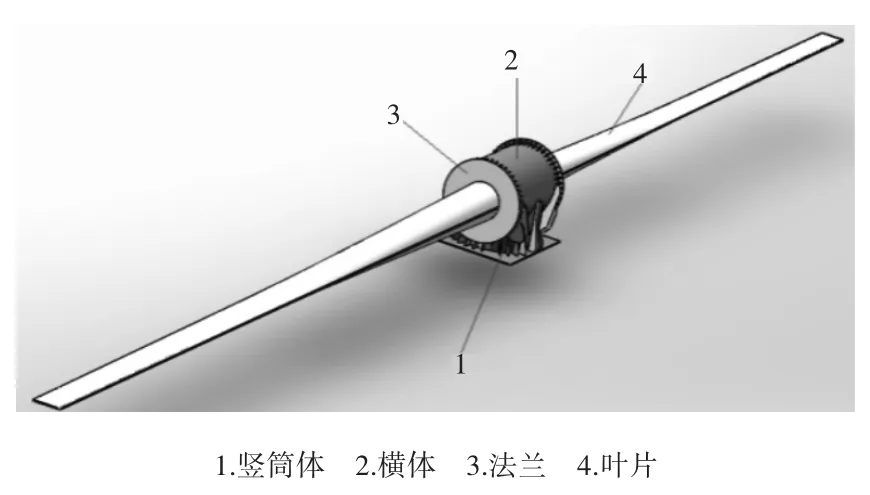
图1 试验台装配模型图

其中横筒体内外环截面尺寸分别为φ4 500 mm和φ4 420 mm，长度为5 600 mm；竖筒体内外环截面尺寸分别为φ4 500 mm和φ4 420 mm；法兰直径为φ5 000 mm，厚度为54 mm.横筒体、竖筒体和法兰材料均为结构钢。

叶片模型1如图2所示，其端部圆环截面尺寸分别为φ2 350 mm和φ1 800 mm，整个叶片长度为56.5m.叶片模型2如图3所示，其端部圆环截面尺寸为φ1 850 mm和φ1 400 mm，整个叶片长度为40 m.叶片材料参数均为：密度为1 200 kg·m3，弹性模量为1.61E+10 Pa，泊松比为0.2.

图2 叶片模型1

图3 叶片模型2

3 模态分析

3.1 风机叶片模态分析

把叶片模型1和2分别导入到Ansys workbench中，进行模态分析：网格尺寸为100 mm，Relevance center设置为Fine，在叶根处施加固定约束，其余按默认设置。计算得到叶片模型1的模态参数，如图4所示。

图4 叶片模型1的模态分析结果

叶片模型1的一阶模态为Y方向的弯曲方向；二阶模态为X方向的扭转方向；三阶模态为Y方向的二次弯曲方向；四阶模态为Y方向的三次弯曲方向。与实际工况相比，得到：叶片上下弯曲时固有频率0.482 2 Hz，左右扭转时固有频率1.012 5 Hz.计算固有频率与厂家试验大纲中的0.479 1 Hz和0.823 3 Hz较为接近，符合实际情况，可以用来后续研究。

叶片模型2的分析步骤与叶片模型1相同，模态分析结果如图5所示。

（续下图）

（续上图）

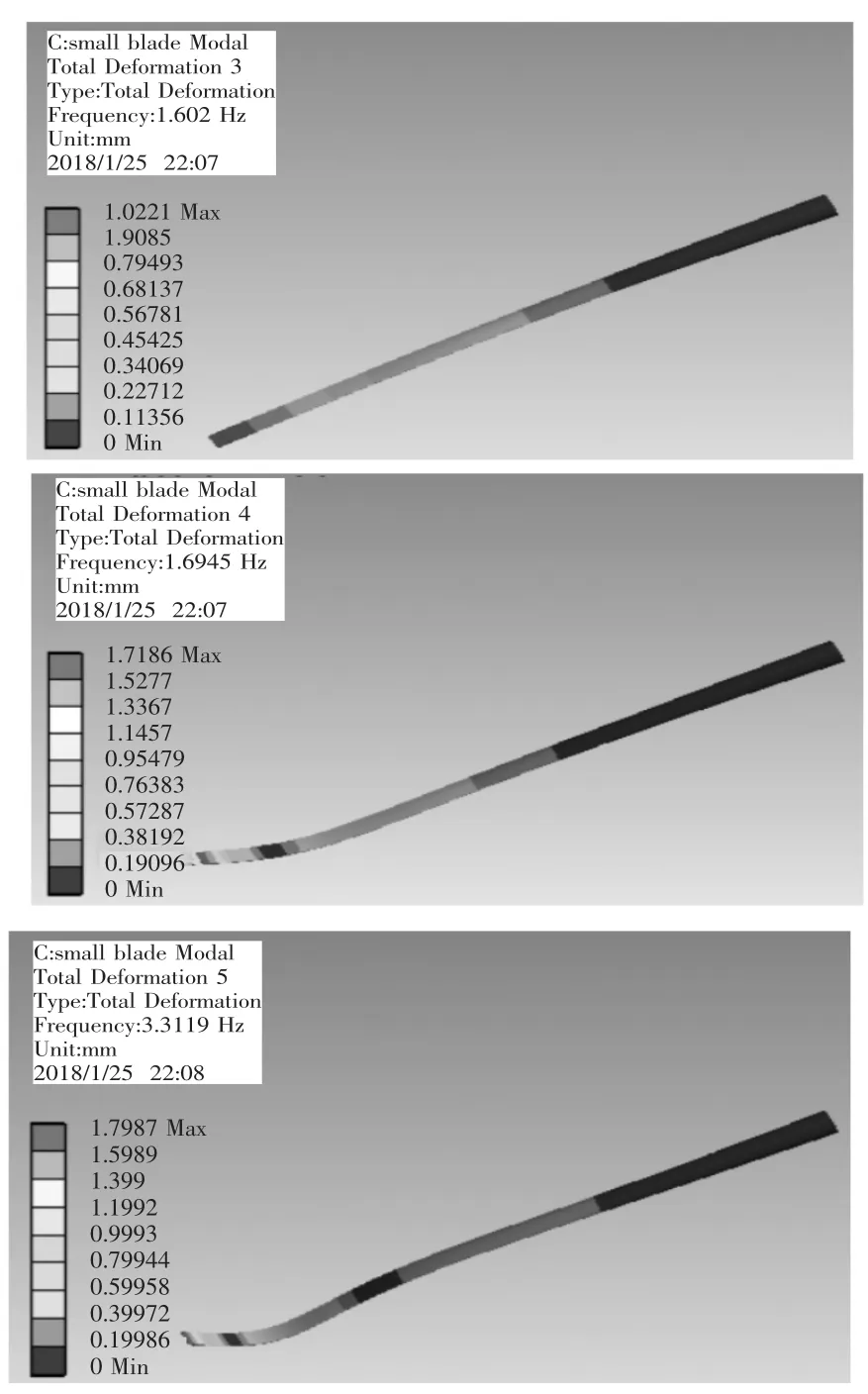
图5 叶片模型2的模态分析结果

叶片模型2的一阶模态为Y方向的弯曲方向；二阶模态为X方向的扭转方向；三阶模态为Y方向的二次弯曲方向；四阶模态为Y方向的三次弯曲方向。与实际工况相比，得到：叶片上下弯曲时固有频率为0.71019 Hz，左右扭转时固有频率为1.62 Hz.

3.2 风机叶片试验台基座模态分析

风机叶片试验台基座由横筒体和竖筒体构成。对试验台基座进行模态分析：网格尺寸为80 mm，Relevance center设置为Fine，在基座底部施加固定约束，材料为结构钢，其余按默认设置。计算得到风机叶片试验台基座的前四阶模态参数，如图6所示。

（续下图）

（续上图）

图6 钢结果筒体模态

以竖直法兰面为正方向，风机叶片试验台基座的一阶模态为左右弯曲方向；二阶模态为上下弯曲方向；三阶模态为左右扭转方向；四阶模态为上下拉伸方向。与实际工况相比，得到：基座上下弯曲（方向为横筒体轴向）时，固有频率为44.375 Hz；左右扭转（方向为竖直方向）时，固有频率为68.534 Hz.

对应于实际工况，基座固有频率最小为44.375 Hz，叶片最小固有频率为0.482 2 Hz，机座固有频率为叶片固有频率的的110倍，筒体固有频率远大于叶片固有频率，两者不会产生共振。

4 频率干涉分析

4.1 相同叶片频率干涉分析

试验台筒体两侧安装相同叶片1，当一侧叶片1固定，另一侧叶片1在距叶跟25 m处施加5 000 N（竖直向上）的力，基座底部施加固定约束，对该模型进行有限元分析。加载如图7所示。

图7 两侧安装叶片1加载图

得到各叶片在各激振力下的变形如图8和图9所示：左边叶片1变形情况：25m处，0.53 Hz时，单边变形达到269 mm.56.5 m处，0.53 Hz时，单边变形达到8 270mm.

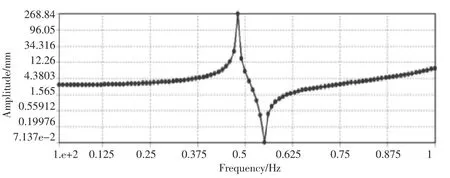
图8 左边叶片25m处不同频率下的幅值

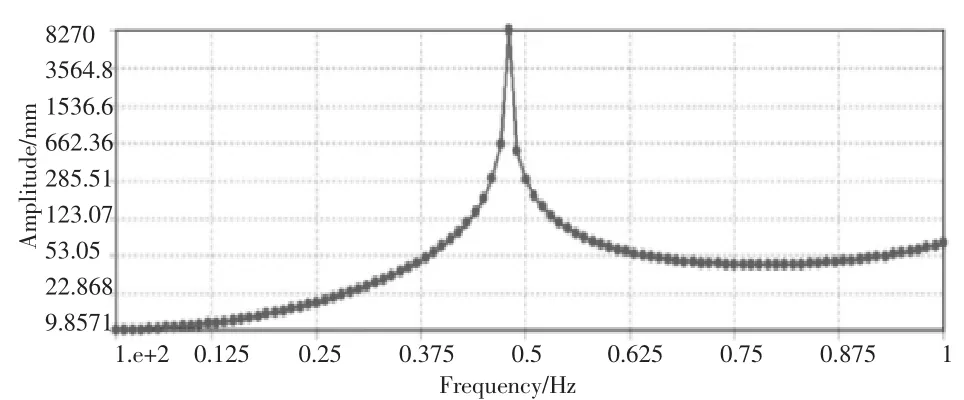
图9 左边叶片56.5m处不同频率下的幅值

右边叶片1变形情况如图10所示：56.5 m处，0.53 Hz时，单边变形达到3 158mm.

图10 右边叶片56.5m处不同频率下的幅值

可以看出，两边叶片相同时，一边叶片振动会引起另一边叶片的共振，左边激励叶片在56.5 m处的振幅为8 270mm；而右边干涉叶片在56.5 m处的振幅为7 153 mm，两边叶片振幅接近，共振情况严重。

4.2 不同叶片频率干涉分析一

试验台筒体两侧安装不同叶片，当一侧叶片2固定，另一侧叶片1在距叶跟25 m处施加5 000 N（竖直向上）的力，基座底部施加固定约束，对该模型进行有限元分析。

得到各叶片在各激振力下的变形如图11和图12所示：叶片1变形情况：25 m处，0.48 Hz时，单边变形达到229 mm；56.5 m处，0.48 Hz时，单边变形达到7 034mm.

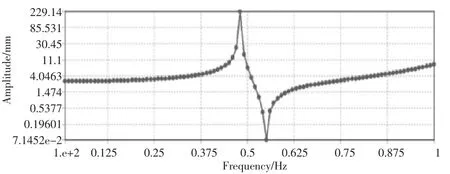
图11 叶片1在25m处不同频率下的幅值

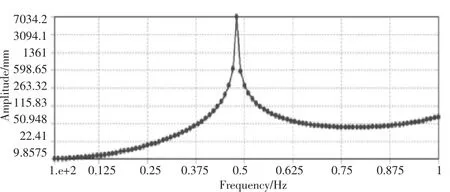
图12 叶片1在56.5m处不同频率下的幅值

叶片2变形情况如图13所示：40 m处，0.71 Hz时，单边变形达到23 mm.

图13 叶片2在40m处不同频率下的幅值

可以看出，两边叶片不同且刚度小的叶片作为激励时，刚度大的叶片也会因为干涉产生振动，但振动变形较小，激励叶片1在56.5 m处的振幅为7 034 mm；而干涉叶片2在40 m处的振幅为23 mm，单位长度变形仅为0.5 mm/m，且两边变形幅值相差300多倍，故激励叶片对干涉叶片影响较小。

4.3 不同叶片频率干涉分析二

试验台筒体两侧安装不同叶片，当一侧叶片1固定，另一侧叶片2在距叶跟40 m处施加5000 N（竖直向上）的力，基座底部施加固定约束，对该模型进行有限元分析。

叶片2变形情况如图14所示：40 m处，0.71 Hz时，单边变形达到107 750mm.

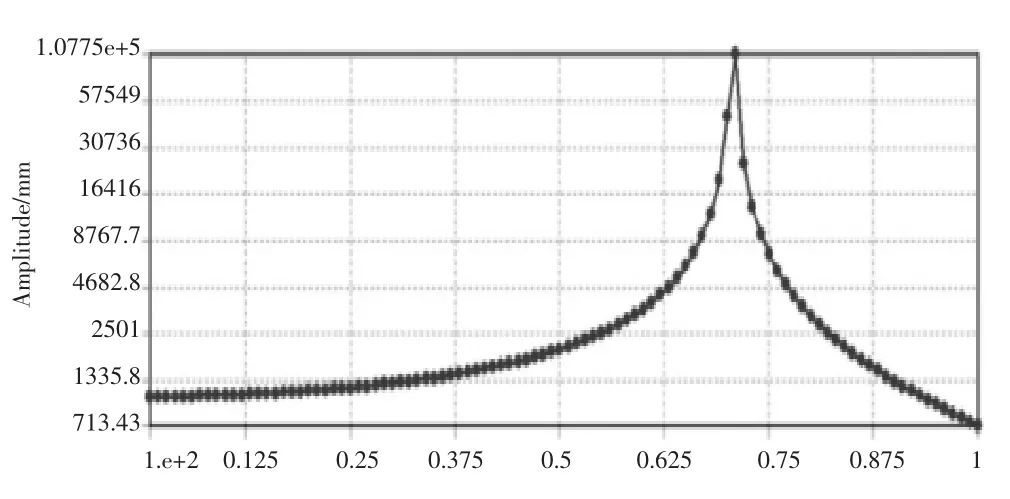
图14 叶片2在40m处不同频率下的幅值

叶片1变形情况如图15和16所示：25 m处，0.48 Hz时，单边变形达到23 mm；56.5 m处，0.48 Hz时，单边变形达到279mm.

图15 叶片1在25m处不同频率下的幅值

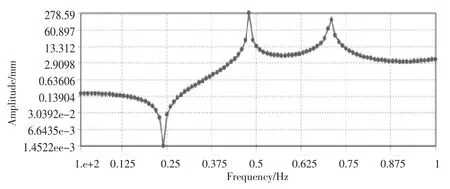
图16 叶片1在56.5m处不同频率下的幅值

可以看出，两边叶片不同且刚度小的叶片作为激励时，刚度大的叶片也会因为干涉产生振动，但振动变形较小，激励叶片2在40 m处的振幅为107 750 mm；而干涉叶片1在56.5 m处的振幅为279 mm，单位长度变形仅为4.9mm，且两边变形幅值相差4000多倍，故激励叶片对干涉叶片影响较小。

5 结束语

综上可知，在固有频率相差较大的叶片同时做疲劳试验时，大小规格的叶片对彼此另一端的叶片振动干涉都较小；而固有频率相同或接近时，叶片对彼此另一端的叶片振动干涉都较大。故风机叶片试验台两边安装叶片，做疲劳试验时，两边应采用规格尺寸相差较大的风机叶片，以保证相同方向的固有频率保持较大的差异，文中两者频率相差1.48倍，能很好的降低频率干涉的影响。叶片筒体的固有频率应远大于叶片的固有频率，才能够保证足够的刚度，降低基座受到的振动干涉，以及降低相连叶片受到的影响，文中对应工况的基座频率为叶片频率的110倍。

[1]杨 阳．基于振动测试的掘进机关键结构动态特性研究[D]．北京：中国矿业大学，2016.

[2]阮文苏.双质体振动给料机动态设计研究[D].北京：中国矿业大学，2013.