板式换热器结构参数优化设计

潘旭，姜未汀，黄永帅，韩维哲，史文斯

（1-上海电力学院能源与机械工程学院，上海 200090；2-江苏唯益换热器股份有限公司，江苏丹阳 212311）

0 引言

由于全球市场竞争压力不断增加，节约能源和减少环境污染的迫切要求已受到越来越多工业部门的重视。板式换热器作为一种高效的节能设备，在医药、食品、合成纤维、造船、动力、冶金及化工等工业部门发挥着重要作用[1]。近年来，我国北方城市大力推行“煤改电”、“煤改气”等环保政策，进一步加快了换热器行业的发展。

实验测试换热器的换热性能，是行业常用的研究手段。魏文建等[2-3]通过实验对点波板式换热器测试了单相换热和蒸发、冷凝测试，反映了点波板式换热器在换热和流动性能上的优势。随着计算机技术的不断发展，带动着流体力学的不断进步。计算流体动力学（Computational Fluid Dynamics，CFD）是通过计算机数值计算和图像显示，对包含流体流动和传热等相关物理现象的系统进行分析研究，是流体力学的一个分支[4]。目前，CFD已经成为对换热器性能进行优化设计和预测必不可少的工具。GRIJSPEERDT等[5]基于低雷诺数k-ε湍流模型，模拟了板式换热器的换热性能，得到了板式换热器最佳的波纹形状和波纹倾角。GALEAZZO[6]通过使用CFD对四通道板式换热器进行数值模拟研究，并将实验测试结果与CFD模拟得出的热负荷进行比较，结果表明CFD结果与实验测试数据具有良好的吻合性，表明了数值模拟的准确性及有效性，并指出数值模拟可以对板式换热器内部的温度场、速度场进行描绘。蔡毅等[7]通过建立与人字形波纹板片完全相同、含分配区和传热区的冷热双流道换热计算模型，采用计算流体力学软件Fluent 6.3数值模拟4组不同速度下流体的流动和换热情况。通过分析流道内速度场和温度场发现，进口分配区对流体流动分布和换热都有显著影响，两侧流体的压降和进出口温差的计算值与实验值的误差小于6%，较准确地反映了换热器内整体的流动和换热特性，可直接用于板式换热器性能的研究，具有一定的工程实际意义。徐志明等[8]通过建立人字形板式换热器冷热双流道的流体流动与传热计算模型，利用计算流体力学软件对5组不同速度工况下换热器内流体的流动和传热进行了数值模拟，分析了换热器流道内的速度场、温度场和压力场。结果表明数值模拟得到的板式换热器进出口温差和压降与试验测量值的误差均小于6%。

板式换热器性能优化一直是相关领域的研究热点。由于板式换热器换热性能受到多种因素影响，所以有研究者运用多目标规划对板式换热器进行优化研究。NAJAFI等[9]通过MATLAB对系统进行建模，并利用遗传算法实现多目标优化，获得了能够使板式换热器达到最小压降和最大总传热系数的一组设计参数。HILBERT等[10]采用多目标遗传算法对换热器的叶片形状、流动与热传递过程的耦合求解进行优化设计，结果得出板式换热器以最小压损获得最大换热量时的最优几何结构。SANAYE等[11]以板翅式换热器的最大热效率和最小年度总成本为目标函数，采用多目标遗传算法对板翅式换热器的结构参数进行优化设计，结果表明了最大热效率和最小年度总成本之间存在冲突性，优化得出翅片间距、翅片高度、翅片偏移量、热流长度和冷流长度都对最大热效率和最小年度总成本之间的冲突性具有重要影响。蔡飞等[12]利用多目标遗传算法，以传热和压降引起的耗散数最小为目标，对流体出口温度和冷、热流体的流速组合进行了优化。并通过优化实例，表明采用优化解进行换热器设计能够达到较好的运行效果和经济效益。张毅等[13]运用场协同原理对板式换热器单边流动和对角流动时的流动与换热特性进行了分析。通过数值模拟和实验验证表明：在相同的流速下，单边流动的速度场和温度场的协同性及速度场和压力场的协同性较好，得到了单边流动换热效果要优于对角流动，且压降低于对角流动的结论。陈宗毅等[14]采用正交设计研究了波纹深度、波纹倾角、波距对钎焊板式换热器换热性能影响的主次关系，得到一组板片几何优化参数。

在同因素同水平条件下，均匀试验设计安排试验次数远少于正交试验设计安排的试验次数[15]。所以，均匀设计适合于多因素多水平试验。本文根据均匀设计的思想，建立了3因素16水平的试验设计方案，并进行数值计算，对板式换热器结构参数进行优化设计。

1 板式换热器的优化设计

1.1 数值模型

由于板式换热器板片堆叠结构具有周期性和重复性，为了提高工作效率，建立如图1所示的简化数值模型。该模型由上下两个板片组成，形成多个周期性流道。文献[16]指出经过3～5个基本单元，板间流动达到充分发展。

该模型由速度入口、压力出口、恒温无滑移绝热换热壁面和周期性边界组成。入口速度恒定且垂直于入口平面；出口压力设为表压，且考虑回流温度[17]；周期性边界压力和速度场均相同。

图1 板式换热器数值计算模型

1.2 板式换热器性能影响因素分析

根据某一型号钎焊板式换热器进行几何建模和数值计算，数值计算的试验工况为uin=0.2 m/s，Tin= 290.534 K，Twall= 285.65 K。根据工业中板式换热器生产实际情况，各参数试验范围分别是：波纹倾角β= 110°～125°，波纹深度b= 2.05 mm～3.5 mm，波纹间距P= 5.7 mm～7.1 mm。本研究取U16*(1612)均匀设计表拟定数值模拟方案，各因素水平取值如表1所示，依照相对应的均匀设计使用表的安排，表2前4列给出了16组均匀试验的板片结构参数。

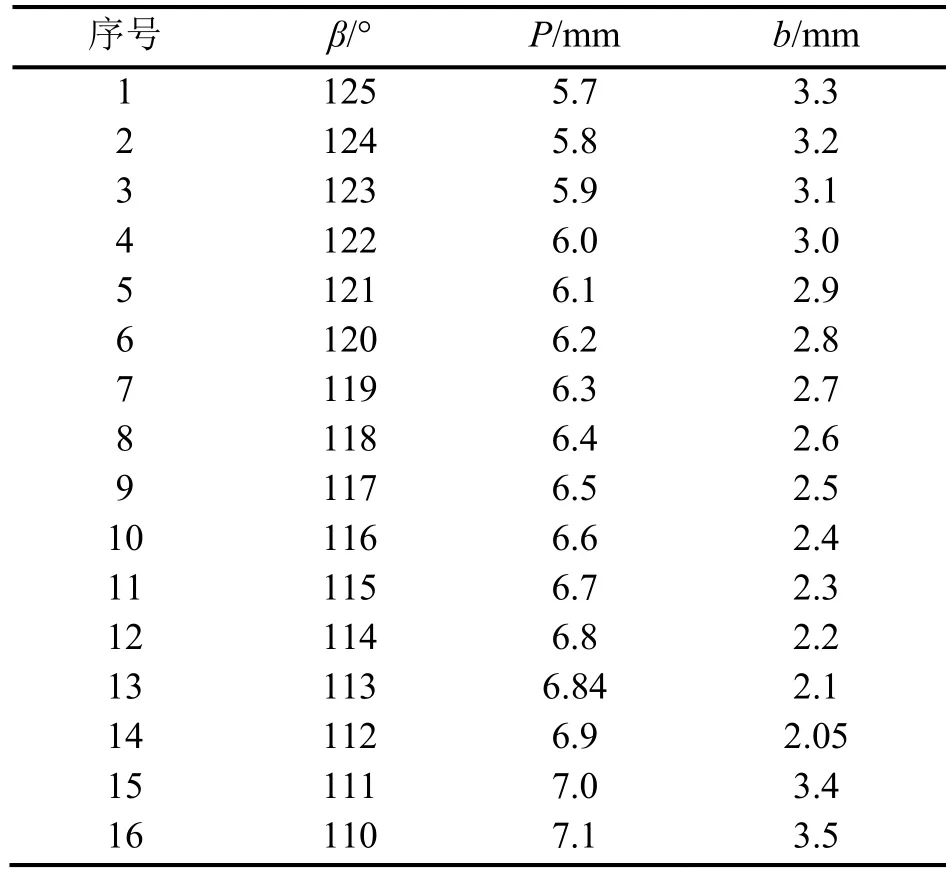
表1 影响因素及水平

1.3 数据处理

单相换热量计算公式按照式(1)～(2)计算，其中流量和进出口温度，直接从模拟结果读取出来，摩擦阻力系数计算公式如式(3)所示：

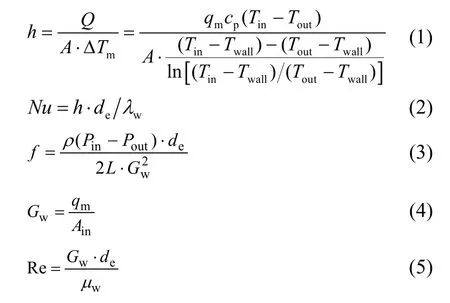
式中：

qm——水的质量流量，kg/s；

cp——水的比热容，kJ/(kg⋅K)；

ΔTm——对数平均温差，K；

Tin——入口温度，K；

思想教育工作是高校各部门、各岗位共同协作下才能有效完成的工作，而辅导员是学生与各部门、各岗位间的最主要桥梁和纽带。在新媒体下学生思想与行为动态的易变性和复杂性，要求辅导员必须提升敏感度，将各类信息及时传递给上级和相关部门，为学校的思想教育工作的相关决策制定和执行提供依据。

Tout——出口温度，K；

Twall——恒定壁面温度，K；

h——对流换热系数，W/(m2⋅K)；

A——换热面积，m2；

de——当量直径，m；

λw——水的导热系数，W/(m⋅K)；

ρ——水的密度，kg/m3；

Pin——进口压力，Pa；

Pout——出口压力，Pa；

L——计算区域沿流动方向的通道长度，m；

Gw——水的质流密度，kg/m2⋅s；

Ain——进口截面积，m2；

Re——雷诺数，无因次；

μw——水的动力粘度，Pa⋅s。

采用综合传热性能因子ψ=Nu/f1/3对板式换热器进行性能评价，ψ越大，板式换热器的性能越好。另外，还分析了波纹倾角、波纹间距、波纹深度3个因素与单位压降ΔPl、换热系数之间的关系。

式中：

ΔPl——单位长度压降，Pa/m。

根据上述公式，雷诺数、单位压降、换热系数和综合传热性能因子的计算结果如表2所示。

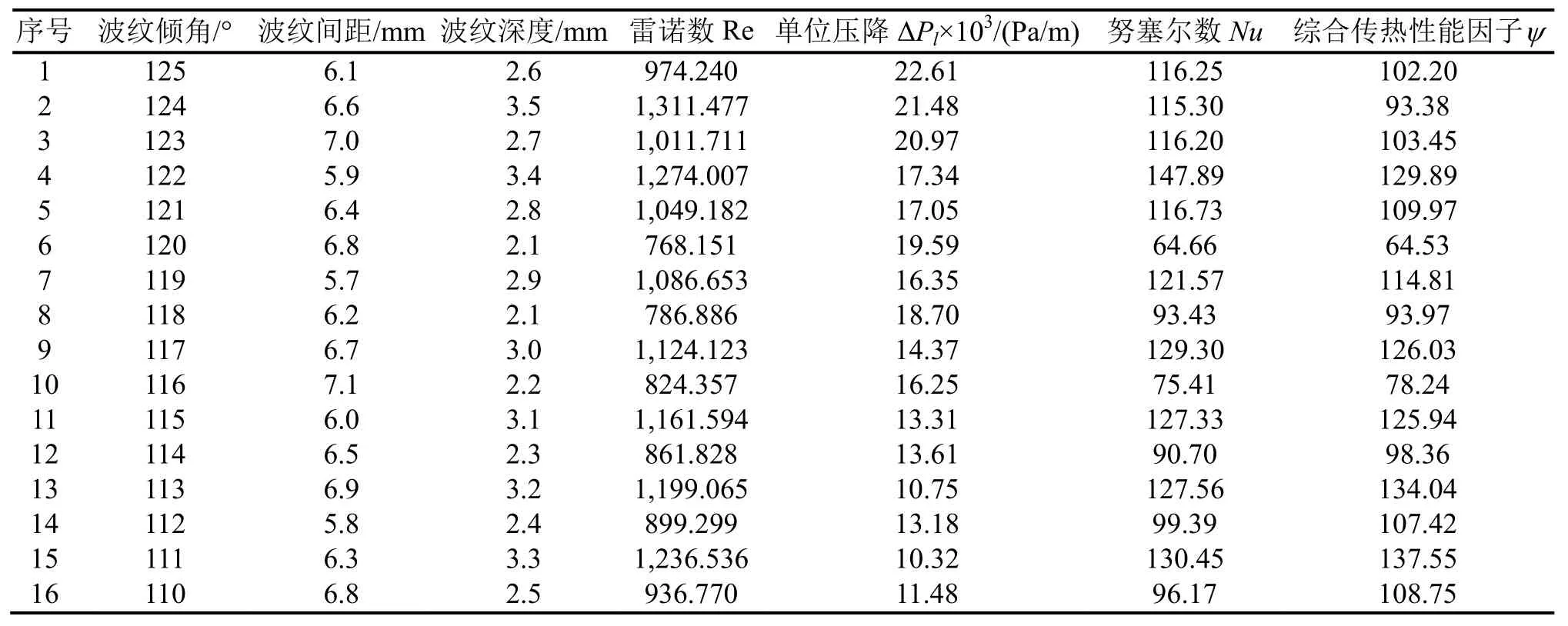
表2 板式换热器结构及性能

2 数据回归分析与优化方案确定

2.1 数据回归分析

根据均匀设计原理，需要对试验数据进行回归分析，进而发现优化的试验条件。本案例选定多元线性回归方法，基于实验设计方案和表2数值模拟得到的计算结果，并利用统计分析软件Minitab获得了Nu、ΔPl和ψ分别与波纹倾角、波纹间距、波纹深度之间的回归关系，如式(7)～(9)所示。在获得式(9)的过程中，采用后退法，逐步剔除对回归方程贡献最小的自变量[19]；在保证回归方程中含有β、P和b这3个影响因素的前提下，最终确定回归方程(9)。

对式(7)～(9)进行误差分析，分析结果如图2～图4所示。根据式(7)计算所得的努塞尔数结果与表2数值计算得到的结果进行误差对比，误差主要分布在±10%内，最大误差为19.78%，平均误差为6.32%。根据式(8)计算所得的单位压降结果与表2数值计算得到的结果进行误差对比，如图3所示，误差均在±10%内，最大误差为9.86%，平均误差为4.4%。根据式(9)计算所得的综合传热性能因子与表2数值计算得到的结果进行误差对比，如图4所示，误差均在±10%之间，最大误差为9.23%，平均误差为4.76%。

由式(7)～(9)可知，由于波纹倾角β增加，流体流动由十字交叉流发展为曲折流，增加了流体的扰动，从而使换热系数增加。同时由于波纹倾角的增加，触点分布密度呈现先增大后减小的趋势，触点密度的变化会导致流体的流态发生扰动，从而增强触点周围的湍流强度，同时压降损失也会增大；间距P增加，换热系数降低，原因是当间距增加时，流体流动更加顺畅，扰动程度降低，此时压降也会降低。而波纹深度b通过改变流道内流体的漩涡混合程度及涡旋区的大小来影响换热阻力性能。

2.2 最优化方案及验证

当综合传热性能因子ψ达到最大值时，表明换热器的换热性能良好。则问题转换为：当β、b和P取值范围为本文研究的范围内时，对式(9)进行最大值求解。计算结果表明，当β=110°、P=5.7 mm和b=3.2 mm时，综合传热性能因子达到最大值ψ1=140.37。

为了进一步验证回归方程中ψ1的正确性，对于得到的最优波纹板结构参数通过Fluent14.0进行数值计算，数值计算的试验工况与上述16次试验时的工况条件一致，得到验证综合传热性能因子ψ2为137.49。通过对比可以看出，数值验证得到的ψ2值与回归方程计算得到的ψ1值极为接近，误差为2%。

图2 Nu数值计算值与回归方程计算值对比

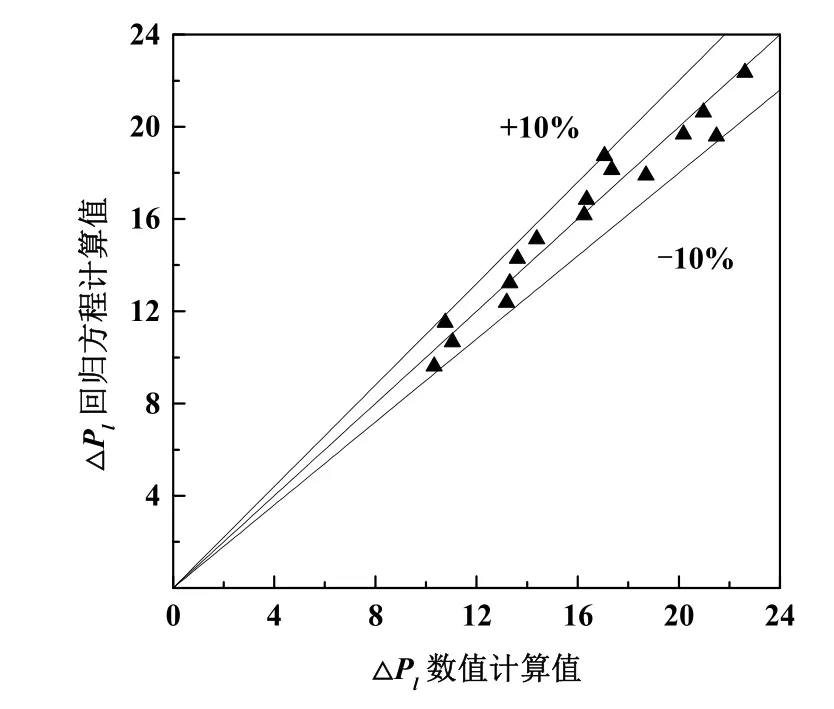
图3 ΔPl数值计算值与回归方程计算值对比

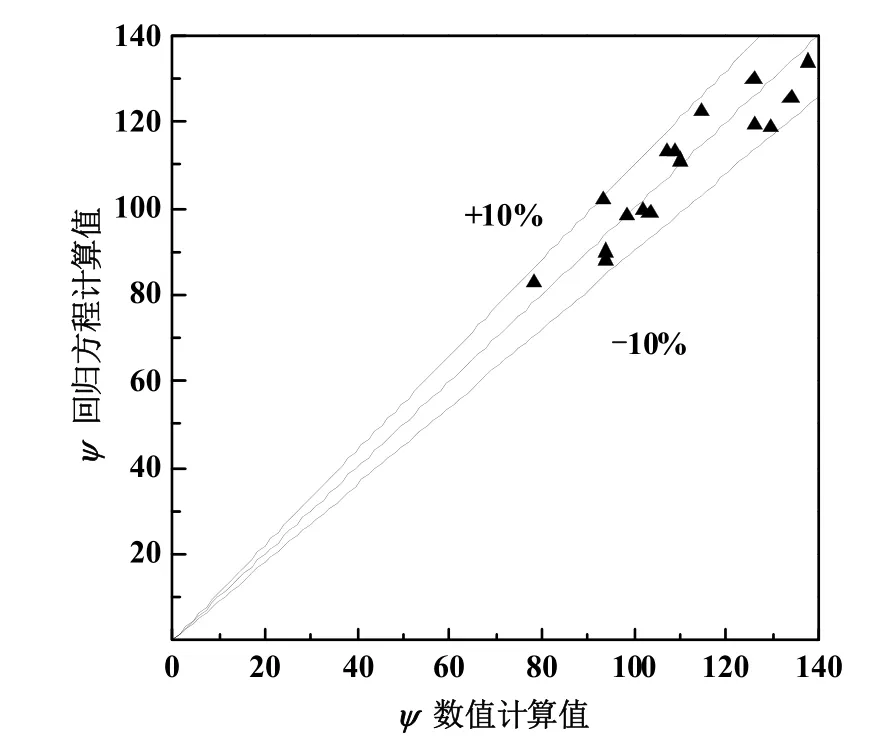
图4 ψ数值计算值与回归方程计算值对比

3 结论

本文介绍了板式换热器波纹结构优化的研究方法，利用均匀设计拟定数值模拟的方案。在参数取值范围内，通过回归分析得到了一组最优参数；当波纹倾角为110°、波纹间距为5.7 mm、波纹深度为3.2 mm时，综合传热性能因子取得最大值，说明此时换热器的换热性能较好，对工程实践有理论指导意义。

[1]余建祖. 换热器原理与设计[M]. 北京: 北京航空航天大学出版社, 2006.

[2]魏文建, 李华. 点波板式换热器内流体流动换热及压降特性的实验研究[J]. 制冷技术, 2012, 32(4): 36-41.

[3]魏文建, 张志锋, 马文勇. 新型高效点波板式冷凝器性能研究[J]. 制冷技术, 2015, 35(2): 22-25.

[4]王福军. 计算流体力学分析-CFD软件原理与应用[M].北京: 清华大学出版社, 2004.

[5]GRIJSPEERDT K, HAZARIKA B, VUCINIC D.Application of computational fluid dynamics to model the hydrodynamics of plate exchangers for milk processing[J]. Journal of Food Engineering, 2003, 57(3):237-242.

[6]GALEAZZO F C C, MIURA R Y, GUT J A W, et al.Experimental and numerical heat transfer in a plate heat exchanger[J]. Chemical Engineering Science, 2006,61(21): 7133-7138.

[7]蔡毅, 贾志刚, 周文学, 等. 人字形波纹板式换热器性能数值模拟的研究[J]. 计算机与应用化学, 2009, 26(1):105-108.

[8]徐志明, 王月明, 张仲彬. 板式换热器性能的数值模拟[J]. 动力工程学报, 2011, 31(3): 198-202.

[9]NAJAFI H, NAJAFI B. Multi-objective optimization of a plate and frame heat exchanger via genetic algorithm[J].Heat and Mass Transfer, 2010, 46(6): 639-647.

[10]HILBERT R, JANIGA G, BARON R, et al.Multi-objective shape optimization of a heat exchanger using parallel genetical gorithms[J]. International Journal of Heat and Mass Transfer, 2006, 49(15): 2567-2577.

[11]SANAYE S, HAJABDOLLAHI H. Thermal-economic multi-objective optimization of plate fin heat exchanger using genetic algorithm[J]. Applied Energy, 2010, 87(6):1893-1902.

[12]蔡飞, 吴吁生. 基于(火积)耗散理论的螺旋板式换热器多目标优化设计[J]. 电力与能源, 2013, 34(1): 24-26.

[13]张毅, 董鹏飞, 孙晓燕, 等. 基于场协同理论的板式换热器性能优化数值研究[J]. 化工机械, 2013, 40(4):487-491.

[14]陈宗毅, 何林. 基于正交试验的钎焊板式换热器优化设计[J]. 现代机械, 2015(1): 25-27.

[15]李想. 板式换热器传热的数值模拟及波纹板参数优化[D]. 哈尔滨: 哈尔滨工程大学, 2013.

[16]ZHANG L Z. Numerical study of periodically fully developed flow and heat transfer in cross-corrugated triangular channels in transitional flow regime[J].Numerical Heat Transfer, 2005, 48(4): 387-405.

[17]张如许, 魏文建, 胡海涛, 等. 单相流体在点波板式换热器内流动与换热的数值模拟[J]. 制冷技术, 2014,34(5): 6-12.

[18]方开泰. 均匀设计及其应用(二)[J]. 数理统计与管理,1994, 13(2): 59-61.

[19]黄莉. 板式换热器波纹参数优化的数值模拟试验研究[D]. 北京: 北京化工大学, 2010.