基于LSSVM的区域卫星高程拟合模型

杨 帆，谢洋洋

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

基于LSSVM的区域卫星高程拟合模型

杨 帆，谢洋洋

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

针对传统GPS高程拟合方法模型单一、计算复杂等问题，提出一种GPS高程拟合算法：采用灰色最小二乘支持向量机高程转换模型，同时采用粒子群算法寻找模型最优参数；并与其他模型对比。实验结果表明，提出的GPS高程拟合算法能够在很大程度上提高利用少量样本数据拟合模型的稳定性与预测精度，使高程拟合更加可靠。

灰色最小二乘支持向量机；粒子群算法；GPS高程拟合；模型优化

0 引言

随着全球定位系统(global positioning system，GPS)技术的发展，其应用已遍及各个工程领域，但是GPS测量获得的是大地高，而在实际工程应用中，基本上都是采用地面点的正常高，2者之间存在高程异常；因此GPS测高系统并不能为具体工程服务。如何精确地拟合高程异常值已经成为GPS高程转换的重要问题。目前高程异常常用的拟合方法有：曲面拟合法、差值曲面、三次曲面模型[1-3]以及新兴的智能算法如神经网络[4]、支持向量机模型[5]等。然而传统拟合方法有模型单一并且需要大量的训练数据等缺点。

最小二乘支持向量机(least square support vector machine，LSSVM)不仅具有支持向量机(support vector machine，SVM)所具有的能够很好解决小样本、非线性以及高维模式识别等时机问题的优点，而且能够将支持向量机的二次规划问题转换到求解线性方程组的问题中，简化了计算的复杂性，使求解的效率得到提高[6-7]。

本文将灰色最小二乘向量机引入到高程转换中，并采用粒子群算法对模型参数进行优化，建立模型，然后与其他模型进行对比分析。

1 灰色最小二乘支持向量机模型

1.1 模型原理

f(x)=wTφ(x)+b。

(1)

式中：φ(x)为映射函数；w为权值向量；b为偏差量。

由结构风险最小化原理，回归问题转化为

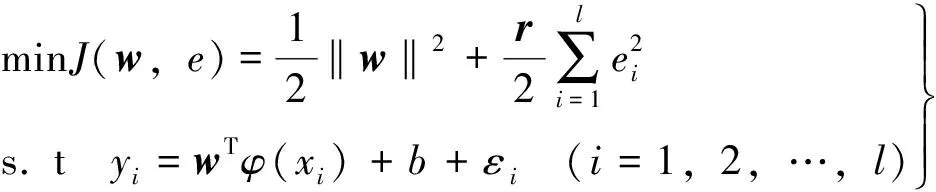
(2)

式中：r为正则化参数；εi为误差量，ei为松弛因子。构造其拉格朗日函数为

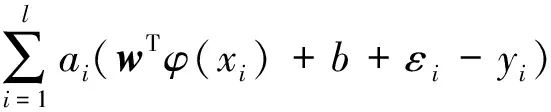
(3)

式中ai(i=1，2，…,l)为拉格朗日乘子。通过卡罗需-库恩-塔克(Karush-Kuhn-Tucker，KKT)最优化条件对其求偏导数可得线性方程组为

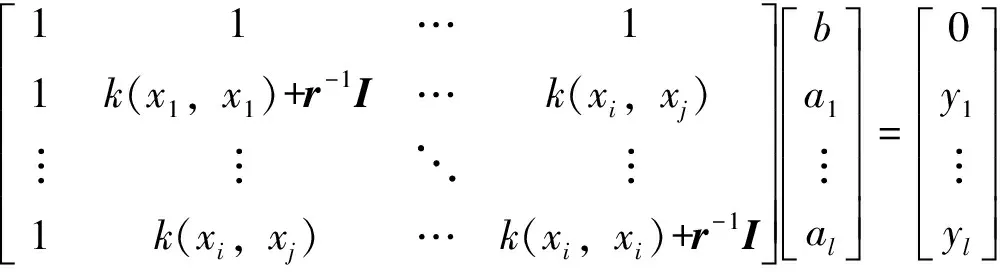
(4)

式中：y=[y1，y2，…，yl]；I表示单位矩阵；k(xi，yi)表示核函数，其表达式为

k(xi，yi)=φ(xi)·φ(xj)；

(5)

求解可得LSSVM回归模型函数估计模型为

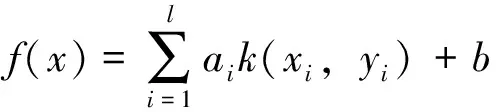
(6)

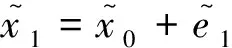
(7)

1.2 基于粒子群优化算法(PSO)的LSSVM参数优化

如前叙述可知，最小二乘支持向量机模型预测的精度主要取决于核函数k(x，y)、核参数σ以及正则化参数γ；因此选择最优的参数组合(σ，γ)尤为重要。粒子群优化算法(particleswarmoptimization，PSO)是模拟鸟群的捕食行为，通过迭代搜寻全局最优值的方法[8-9]。该方法概念简单，计算效率更高，并且更加容易实现。在PSO算法中，vi=(vi1，vi2，…，vin)为粒子i的速度向量，ui=(ui1，ui2，…，uin)为其位置向量，qi=(qi1，qi2，…，qin)为其最好的位置；ug=(ug1，ug2，…，ugn)表示种群所经过的最好位置。位置、速度的更新公式为

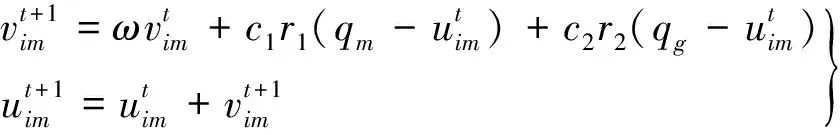
(8)

采用粒子群算法搜寻最小二乘支持向量机的最优参数组合，能够克服传统优化方法的缺点。目前常用的优化方法主要有网格搜索法、遗传算法等等。网格搜索法是将(σ，γ)在一定范围内划分网格并对网格内的所有点进行取值从而寻找最有参数；由于网格众多该方法耗费时间比较长，效率比较低[10]。遗传算法采用启发式算法，无需搜寻整个区间内的参数组合就能得到全局最优解；但是该方法操作复杂并且极易陷入局部最优[11]。因此本文采用粒子群算法寻找最优参数组合，其具体步骤为：

1)根据数据序列建立训练样本与测试样本集；

2)参数的初始化，初始化粒子的速度及位置、学习因子c1、c2及惯性权重ω，学习因子的值分别为1.5、1.7，并且每一个位置有一组参数(σ，γ)与之对应，然后由参数以及训练样本建立LSSVM预测模型；

4)将每个粒子的适度值与自身最优值进行比较，判断是否满足迭代条件，如果满足则得到最优参数(σ，γ)，否则继续执行步骤5)进行迭代计算；

5)根据公式更新粒子的速度和位置，然后转到步骤3)；

6)由得到的全局最优粒子参数(σ，γ)建立LSSVM模型。

2 实例分析

为验证模型的有效性及可行性，选取沿江区域作为研究区域。该区域地势平缓，且GPS控制网稳定性较好并具有40组相同精度的水准高程点。按照国家D级GPS网进行实测，采用四等水准进行GPS联测，得到各点的平面位置与高程异常；以17个平均分布的点作为训练样本，剩余的23个点作为测试样本。各个点的位置分布如图1所示。

2.1 实验过程

将17个平均分布点的高程异常进行归一化处理，作为模型的输入样本，设置模型的初始参数，并选用径向基核函数(RadicalBasisFunction，RBF)。然后采用灰色最小二乘支持向量机模型进行预测分析，同时采用粒子群算法寻找模型的参数，经过计算得到模型的最优参数为：γ=69.576，σ=0.089，p=6。然后与最小二乘支持向量机(LSSVM)、遗传小波神经网络进行对比分析，并计算各个模型的外符合精度。模型高程异常拟合残差如图2所示，拟合异常值及残差如表1所示。

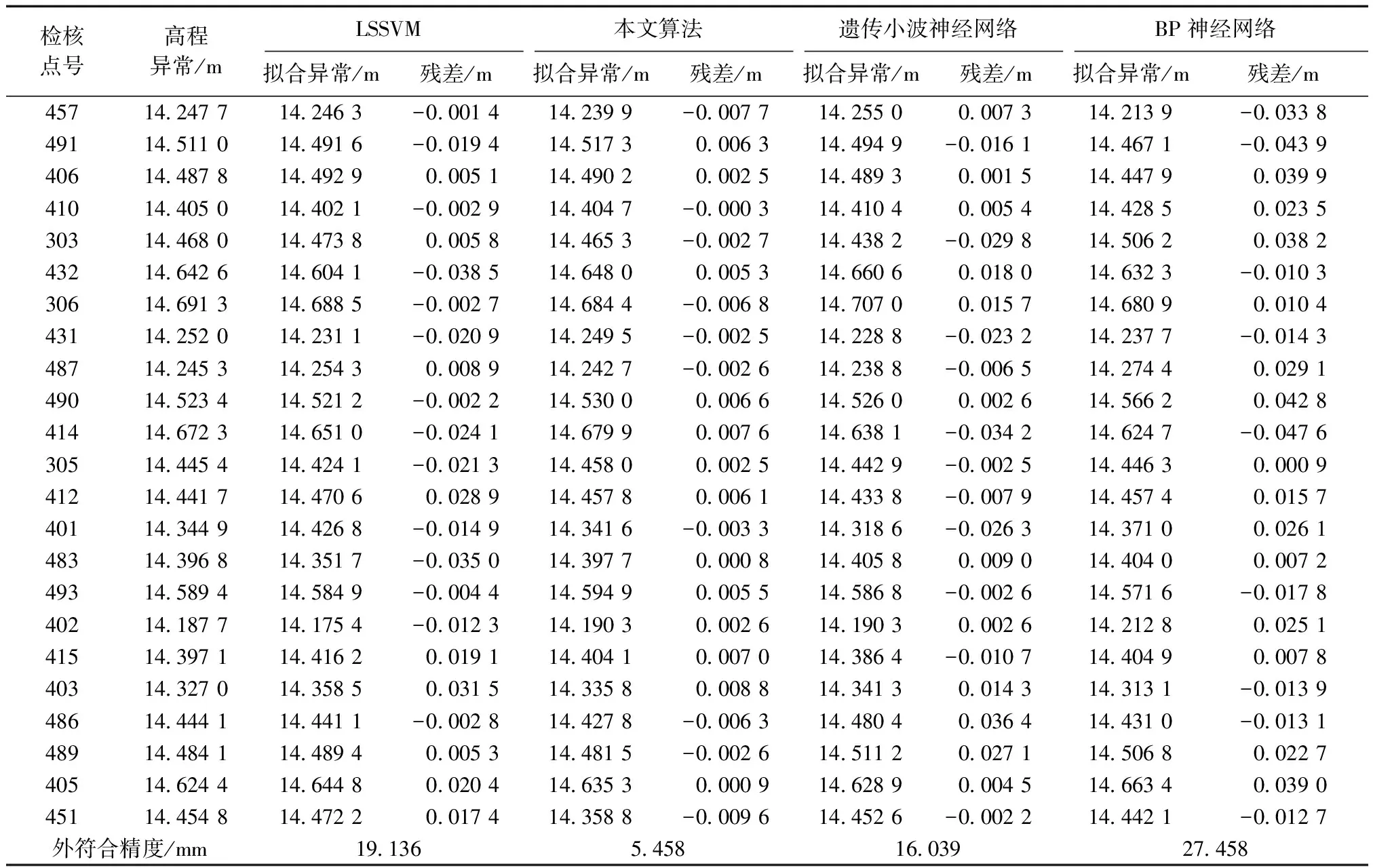
检核点号高程异常/mLSSVM本文算法遗传小波神经网络BP神经网络拟合异常/m残差/m拟合异常/m残差/m拟合异常/m残差/m拟合异常/m残差/m457142477142463-00014142399-0007714255000073142139-00338491145110144916-0019414517300063144949-00161144671-0043940614487814492900051144902000251448930001514447900399410144050144021-00029144047-00003144104000541442850023530314468014473800058144653-00027144382-0029814506200382432146426146041-003851464800005314660600180146323-00103306146913146885-00027146844-000681470700015714680900104431142520142311-00209142495-00025142288-00232142377-0014348714245314254300089142427-00026142388-0006514274400291490145234145212-00022145300000661452600002614566200428414146723146510-0024114679900076146381-00342146247-00476305144454144241-0021314458000025144429-00025144463000094121444171447060028914457800061144338-0007914457400157401143449144268-00149143416-00033143186-0026314371000261483143968143517-00350143977000081440580009014404000072493145894145849-0004414594900055145868-00026145716-00178402141877141754-001231419030002614190300026142128002514151439711441620019114404100070143864-0010714404900078403143270143585003151433580008814341300143143131-00139486144441144411-00028144278-0006314480400364144310-0013148914484114489400053144815-0002614511200271145068002274051462441464480020414635300009146289000451466340039045114454814472200174143588-00096144526-00022144421-00127外符合精度/mm1913654581603927458

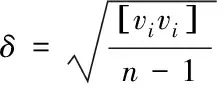
2.2 成果分析

从图2以及表1可知：BP神经网络的拟合精度相对较低，并且残差的波动性相对较大，最大残差为43.9 mm，残差平均值为21.53 mm；LSSVM的拟合精度次之，模型外符合精度为19.136 mm，最大值达到38.5 mm，残差平均值为15.01 mm；遗传小波神经网络高程拟合的残差最大值为36.4 mm，最小为-2.2 mm，残差平均值为13.2 mm；而本文提出的模型高程拟合的外符合精度只有5.458 mm，残差最小值仅为0.3 mm，高程拟合残差平均值仅为4.663 mm，并且从残差图可知本文模型相对比较稳定，模型不仅克服了LSSVM模型参数选择随机性并且避免了其容易陷入局部最优的缺点，能够在很大程度上提高模型的稳定性与预测精度，更好地与实测值相吻合。

3 结束语

本文研究了基于灰色最小二乘支持向量机的区域卫星高程拟合模型，提出的优化模型不仅能够克服单一模型拟合的不足，同时结合灰色模型与粒子群优化算法，可以在很大程度上提高模型的稳定性与预测精度，使高程拟合更加可靠，为GPS高程拟合研究提供参考。

需要说明的是，本文研究区处于地势平缓的地区，因此在地势起伏比较大的区域仍需要进一步验证；同时由于结合多种模型，在一定程度增加了模型的复杂度，所以关于如何进一步优化模型运行的效率与性能，从而建立更为精准的拟合模型，还需进一步研究。

[1] 周忠谟，易杰军，周琪.GPS卫星测量原理与应用[M].北京：测绘出版社，1997：238-240.

[2] 华锡生，黄腾.精密工程测量技术及应用[M].南京：河海大学出版社，2008：120-125.

[3] 刘长建，柴洪洲，吴洪举，等.GPS水准拟合模型的选取与精度估计[J].测绘科学，2009，34(4)：80-81.

[4] 韩硕.神经网络在GPS高程拟合中的应用[J].测绘通报，2006(4)：48-50.

[5] 谢波，刘连旺.支持向量机在GPS高程异常中的应用[J].测绘科学，2011，36(1)：172-174.

[6] 李潇，徐进军.基于小波分析与LSSVM的滑坡变形预测[J].大地测量与地球动力学，2009，29(4)：127-130.

[7] SUYKENS J A K，VANDEWALLE J，MOOR B D.Optimal control by least squares support vector machines[J].Neural Networks，2001，14(1)：23-35.

[8] 曹净，丁文云，赵党书，等.基于PSO-LSSVM模型的基坑变形时间序列预测[J].控制工程，2015，22(3)：475-480.

[9] 黄磊，张书毕，王亮亮，等.粒子群最小二乘支持向量机在GPS高程拟合中的应用[J].测绘科学，2010，35(5)：190-192.

[10]任超，梁月吉，庞光锋，等.基于灰色最小二乘支持向量机的大坝变形预测[J].大地测量与地球动力学，2015，35(4)：608-612.

[11]马文涛.基于灰色最小二乘支持向量机的边坡位移预测[J].岩土力学，2010，31(5)：1670-1674.

Discussion on satellite positioning elevation fitting based on LSSVM

YANGFan，XIEYangyang

(School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China)

Aiming at the problem that traditional GPS elevation fitting is with single model and complex computation，the paper proposed a GPS elevation algorithm：the grey least square support vector machine elevation transformation model was adapted，and the particle swarm optimization algorithm was used to find the optimal model parameters；then other models were compared with it.Experimental results showed that the proposed GPS elevation fitting algorithm could improve the stability and prediction accuracy of the model with little sample data for elevation fitting.

grey least square support vector machine；particle swarm optimization algorithm；GPS elevation fitting；model optimizing

2016-05-09

国家自然科学基金项目(50604009)；辽宁省“百千万人才工程”人选资助项目(2010921099)。

杨帆(1972—)，男，湖北随州人，博士，教授，研究方向为变形监测与预报、开采沉陷研究。

谢洋洋(1991—)，男，江苏淮安人，硕士生，研究方向为变形监测与预报、变形监测数据处理。

杨帆，谢洋洋.基于LSSVM的区域卫星高程拟合模型[J].导航定位学报，2017，5(1)：100-102,114.(YANG Fan，XIE Yangyang.Discussion on satellite positioning elevation fitting based on LSSVM[J].Journal of Navigation and Positioning，2017，5(1)：100-102,114.)

10.16547/j.cnki.10-1096.20170121.

P228

A

2095-4999(2017)01-0100-04