基于无迹卡尔曼滤波器的雷达测距算法研究
熊奎允+胡晓阳
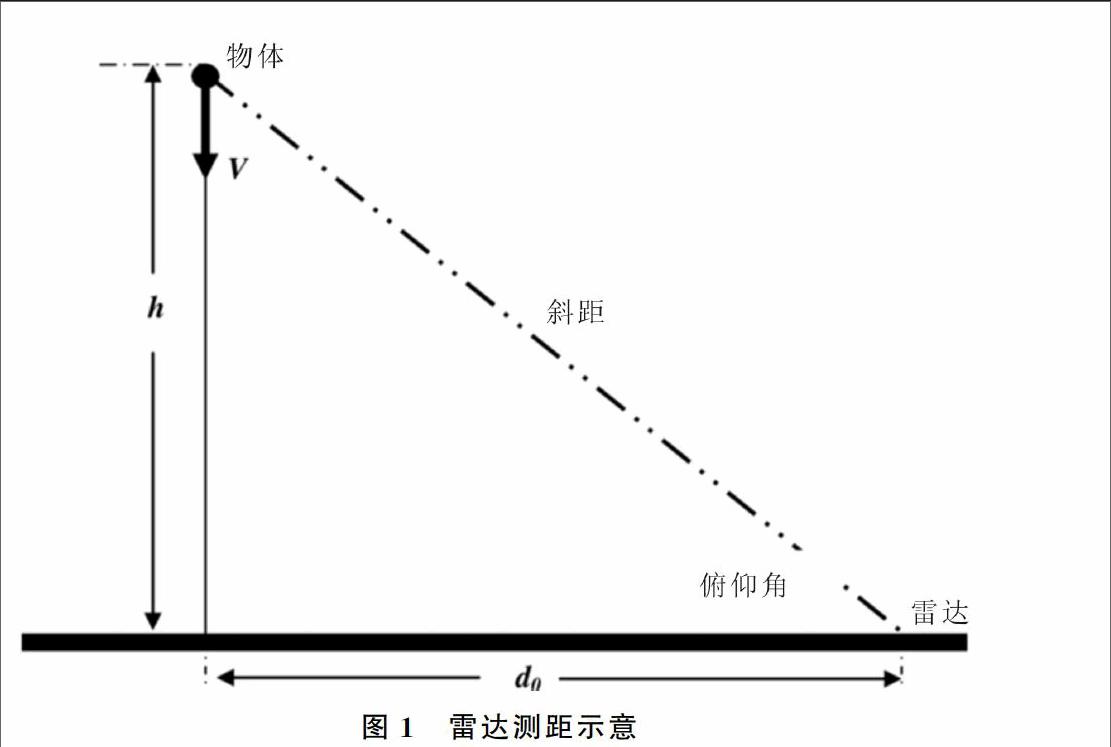

摘要摘要:广义卡尔曼滤波(EKF)在进行数据处理时,仅对测距系统和量测方程作泰勒级数展开且仅保留线性项,因而EKF只适用于弱非线性对象的估计,被处理对象的非线性越强,引起的估计误差就越大,甚至会引起滤波发散。将无迹卡尔曼滤波(UKF)应用于非线性系统的目标处理。通过UKF在雷达测距中的应用和仿真结果分析表明,与EKF相比,UKF收敛快、对噪声适应能力更强且算法实现更简单。自适应无迹卡尔曼滤波(AUKF)可以对系统模型进行实时估计,通过分析知道无迹卡尔曼滤波算法满足实时性跟踪要求,实现了对运动目标的快速跟踪。
关键词关键词:广义卡尔曼滤波(EKF);无迹卡尔曼滤波(UKF);自适应卡尔曼滤波(AUKF);雷达测距;目标跟踪
DOIDOI:10.11907/rjdk.162252
中图分类号:TP312文献标识码:A文章编号文章编号:16727800(2017)001003203
引言
近年来,非线性滤波问题备受关注,其在目标跟踪、定位以及参数估计[13]等方面都有广泛应用。对于线性高斯模型而言,卡尔曼滤波是被公认的最优滤波,其通过递推更新有限维统计量来精确计算后验分布。对目标下落速度与距离地面高度的测量,实质上是对目标物体的一种跟踪,这种跟踪易受到地物回波、测量噪声等各种各样随机噪声的干扰[4]。因此,在采集到数据后,有必要对其进行滤波平滑处理,以进一步提高系统精度。
雷达跟踪滤波其实就是在对提取的目标信息进行估计和预测的基础上,建立目标的运动轨迹,分析目标的运动状态、机动效果等。当机动目标模型建立后,就要针对目标进行算法设计。雷达跟踪需要处理的信息种类多种多样,除了目标的位置信息外,还要对目标的移动速度进行估计。雷达跟踪的收敛速度、滤波精度等是需要考虑的问题。在民用领域中由于考虑到雷达的成本问题,对目标的跟踪进行快收敛性、高精度和高稳定性的改良受到成本的制约,因此可以通过研究雷达的跟踪算法来达到目的。通过对目标的运动过程进行建模和分析,同时将传感器采集到的信息作为观测量,进而利用适当的滤波估计算法实现对目标参数或运动状态的估计。本文通过对传统的UKF算法与自适应卡尔曼滤波算法(AUKF)进行对比,分析得出结论。UKF卡尔曼滤波方法是采用采样策略逼近非线性分布的方法。UKF方法采样的粒子点的个数很少,但具体个数根据所选择的采样策略而定。UKF方法的计算量与EKF滤波算法相当,但性能优于EKF滤波。而AUKF滤波算法是一种循环的迭代算法,可以实时估计系统的状态模型。
1雷达测距系统状态方程与量测方程
1.1状态方程
3仿真分析
仿真参数:记物体距离地面的高度为1 950m,物体初始速度为5m/s,重力加速度为10m/s2,P0=[300,1950,0,-5,-10,0]T,且雷达测距和角测的量测噪声是高斯白噪声随机序列,均值为0,方差阵为R=0.050
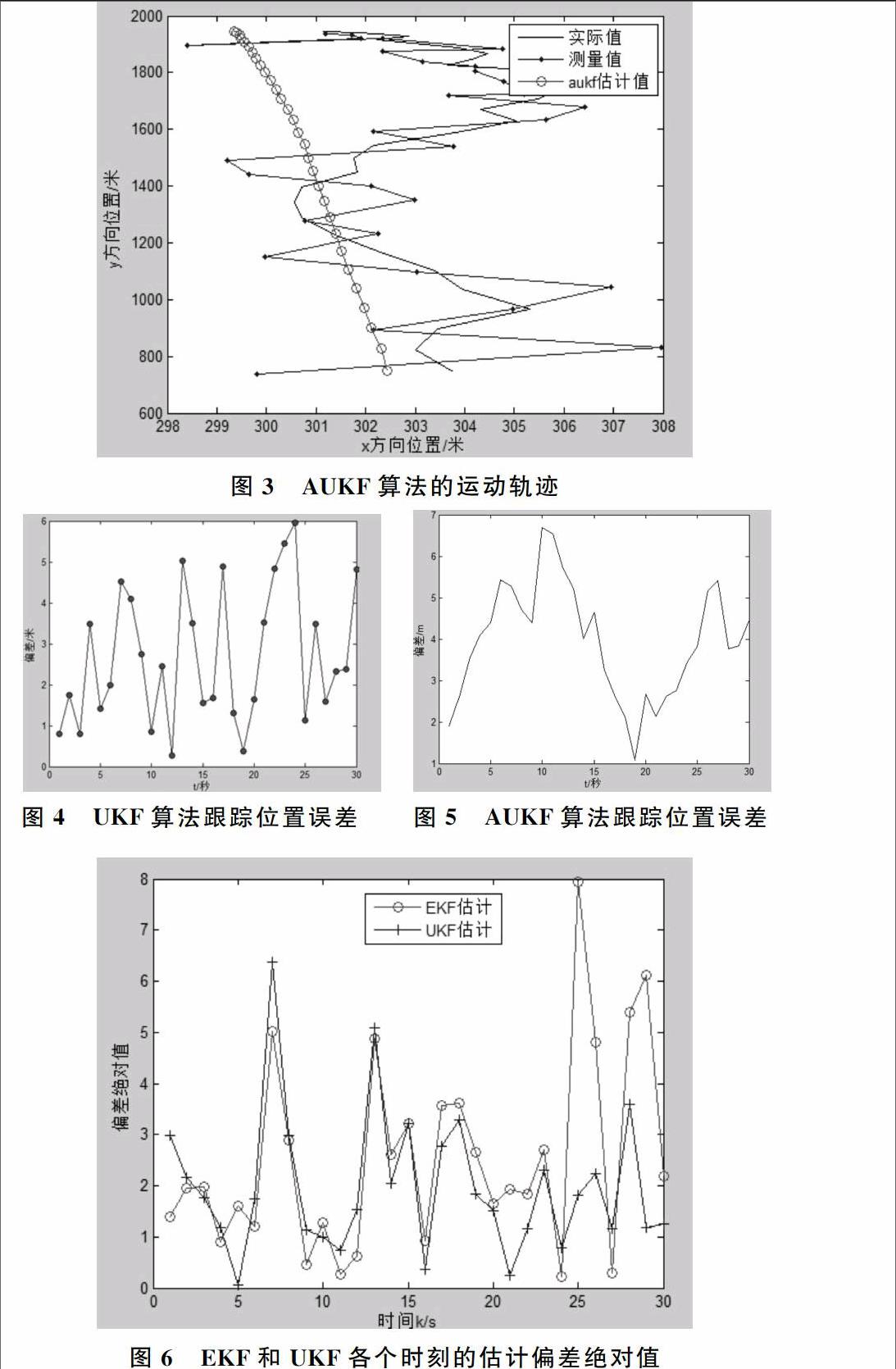
00.02,观测次数N=30。则生成的运动轨迹如图2所示,跟踪位置误差如图3所示,速度位置误差如图4所示,加速度位置误差如图5所示。
由图2可以看出实际值与测量值之间的偏差比较大,经过UKF滤波后的轨迹与实际值的偏差较小。所以采用无迹卡尔曼滤波算法能够更好地反映雷达测距的轨迹。通过图4与图5的对比可以看出,采用AUKF算法的位置跟踪误差在绝大部分时刻要大于采用标准UKF算法的位置跟踪误差。由此可以得出此系统的模型没有很好的自适应性。由图6可以看出,采用UKF滤波后的绝对值偏差比采用EKF滤波的绝对值偏差要小,这表明在状态估计的准确性上UKF优于EKF。因此UKF比EKF有更高的滤波精度。UKF算法有效地克服了扩展卡尔曼滤波的估计精度低、稳定性差的缺陷。
参考文献:
[1]F DAUM.Nonlinear filters beyond the Kalman filter[J].IEEE A&E Systems Magazine,2005,20(8):5769.
[2]李旦,秦永元,梅春波.组合导航自适应卡尔曼滤波改进算法研究[J].测控技术学报,2011,30(3):114116.
[3]戴路,金光,陈涛.自适应扩展卡尔曼滤波在卫星姿态确定系统中的应用[J].吉林大学学报,2008,38(2):467470.
[4]谢宜生.基于微波雷达的高速公路测距测速系统研究[D].杭州:浙江大学,2011.
[5]LEFFERS EJ,MARKLEY F L,SHUSTER M D.Kalman filtering for spacecraft attitude estimation[J].Journal of Guidance, Control and Dynamics,1982,5(5):417428.
[6]S J JULIER,J K UHLMANN.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3): 401422.
[7]段方,刘建业,李荣冰.基于平淡卡尔曼滤波器的微小衛星姿态确定算法[J]. 上海交通大学学报,2005,11(39):18991903.
[8]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2014.
[9]魏克新,陈峭岩.基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J].中国电机工程学报,2014,34(3):445452.

