基于变化率的子空间聚类算法

赵星辉+龙艺璇

摘要摘要：针对低维多流形非相似结构数据，提出一种基于变化率聚类的算法。首先观察数据，按结构对数据进行分类，然后在同构的数据点之间按变化率进行划分，最终实现数据聚类。实验结果证明，该算法能够有效对低维多流形非相似结构数据进行聚类分析，聚类效果明显优于LRR、SSC等传统算法，且时间复杂度较低，有较强的适用性。

关键词关键词：流形学习；子空间聚类；低秩表示法（LRR）；稀疏子空间聚类（SSC）；变化率

DOIDOI：10.11907/rjdk.162181

中图分类号：TP312文献标识码：A文章编号文章编号：16727800（2017）001002903

引言

随着科学技术的发展，各类数据量迅猛增长。然而，并不是所有数据都是精炼且真实有效的，海量数据中存在着冗余与错误。如何对这些数据进行快速、有效的处理，从而找到数据之间的内在联系成为解决很多问题的关键。因此对高维数据进行相关性分析、聚类分析、结构分析，挖掘数据背后的价值与意义尤为重要。

对高维数据进行分析处理，当前应用比较广泛的维数约减技术有流形学习[1]和子空间聚类[2]。流形学习的前提是假设在一个高维欧式空间均匀地对数据进行采样，然后将高维数据映射到低维，使得数据的低维表示能体现高维数据的本质信息[3]；子空间聚类是假设一组数据属于多个线性子空间的并集，将这组数据进行分类，使得不同的类对应不同的子空间。

高维数据的结构一般为低维的，可以用位于相同子空间的低维数据对高维数据进行稀疏表示，因此设计一种能分析低维多流形非相似结构数据的算法更具有一般性和适用性。本文针对低维多流形非相似结构数据，提出一种基于变化率聚类的算法，从而更有效进行聚类分析。

1基于变化率的子空间聚类算法

1.1算法描述

为更好地对低维多流行非相似结构的数据进行聚类分析，本文提出一种基于变化率的子空间聚类算法。该算法的基本思想是：首先观察数据，若数据来源于多个维数不等的数据结构，则先根据按属性重要性筛选出的维对不同结构的数据进行分类；然后在同构数据点之间按其变化率进行划分，若变化率超过一定的阈值β，则分到不同的类中，若小于等于β则分到同一类；最终得到各个不同结构的分类。任意两点之间的变化率为：RC（X，Y） = Yi + 1 -Xi + 1 Yi -Xi （1）算法描述如下：

输入：数据集D，簇数k。

输出：k个簇。

Step1：按一定的准则选择重要属性。

Step2：根据重要属性将不同结构的数据划分开，形成m个中间簇。

Step3：对中间簇中的数据按变化率RC进行分类，如果两点之间的变化率大于β，则划分为不同的类；否则划为一类。

Step4：重复Step3直到中间簇都被划分完。

Step5：输出k个簇。

1.2对比算法选取

在子空间聚类算法中，应用比较多的是基于谱聚类的方法，首先根据样本点之间的关系构造图谱，然后利用NCut[4]等谱聚类方法得到分割结果。基于谱聚类的子空间分割方法中比较有代表性的是低秩表示法（LRR）[5]和稀疏子空间聚类（SSC）[6]算法。

低秩表示法（LRR）算法是为了从包含错误的数据中恢复子空间结构而提出的。在给定的一组数据样本中，每一个都可以被表示为在一个字典中的一个基数线性组合，LRR旨在找到所有共同数据的低秩表示。通过选择一个特定的字典，LRR可以很好解决子空间聚类问题。对于被任意错误污染的数据，LRR还可以近似的恢复行空间，LRR是一个有效的且具有鲁棒性的子空间聚类算法。

稀疏子空间聚类（SSC）可以用来聚类位于低维子空间的并集的数据点。关键思想是，从其它点获得无穷多的可以表示的数据点，并用一个稀疏表示来对应从相同的子空间选择的点。这促进了谱聚类算法框架下用来推断数据的聚类子空间的稀疏优化程序。该算法处理接近于子空间交集的数据点是有效的，另一个关键优势在于它可以通过合并数据的模型到稀疏优化程序来直接处理数据干扰，如噪音、稀疏的无关记录和缺失记录。在运动分割和聚类方面，该算法都具有较高的实用性。

2实验结果与分析

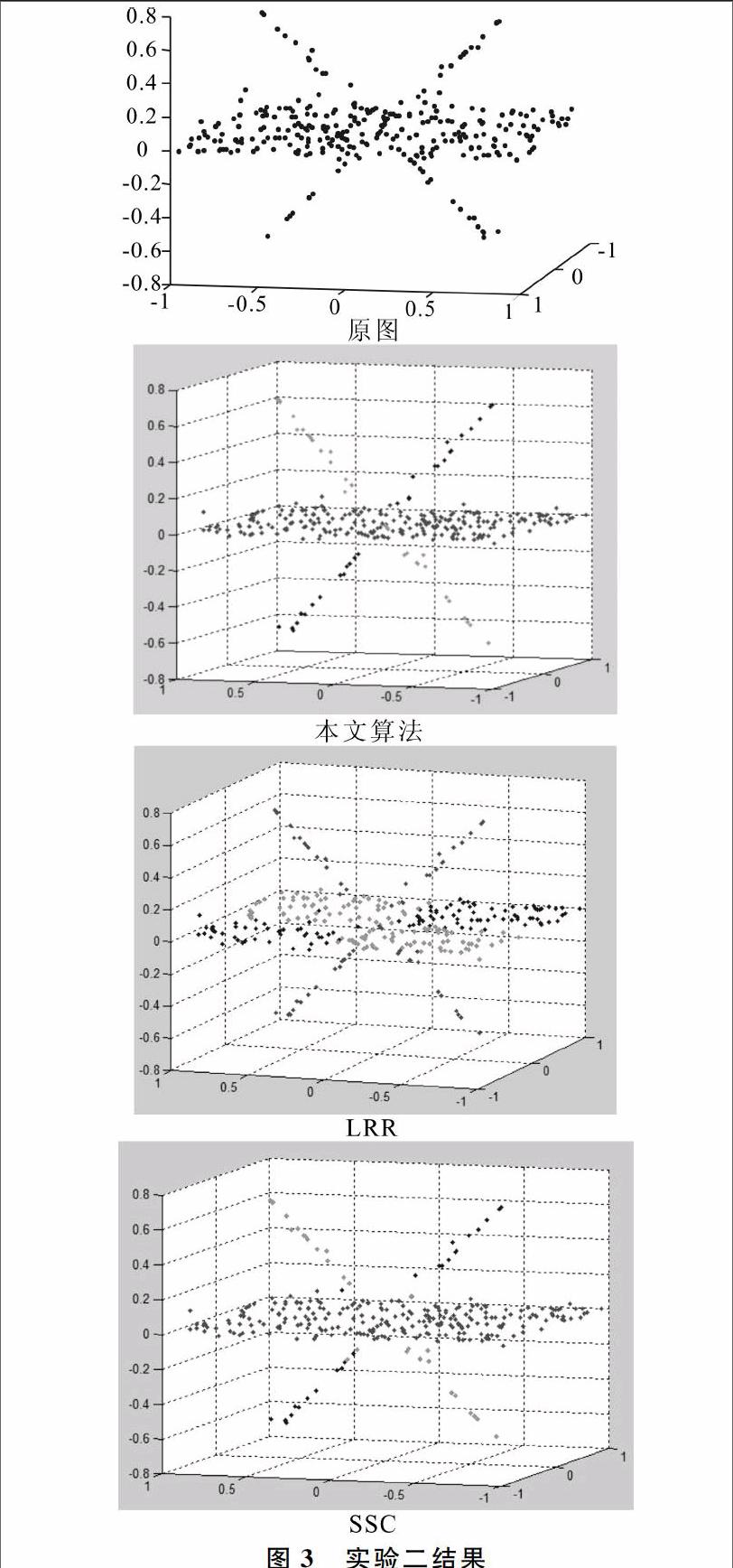
为了验证基于变化率的子空间聚类算法的有效性与实用性，本文选取三幅变化率较为明显的低维多流行结构图进行聚类分析实验。

2.1实验一结果与分析

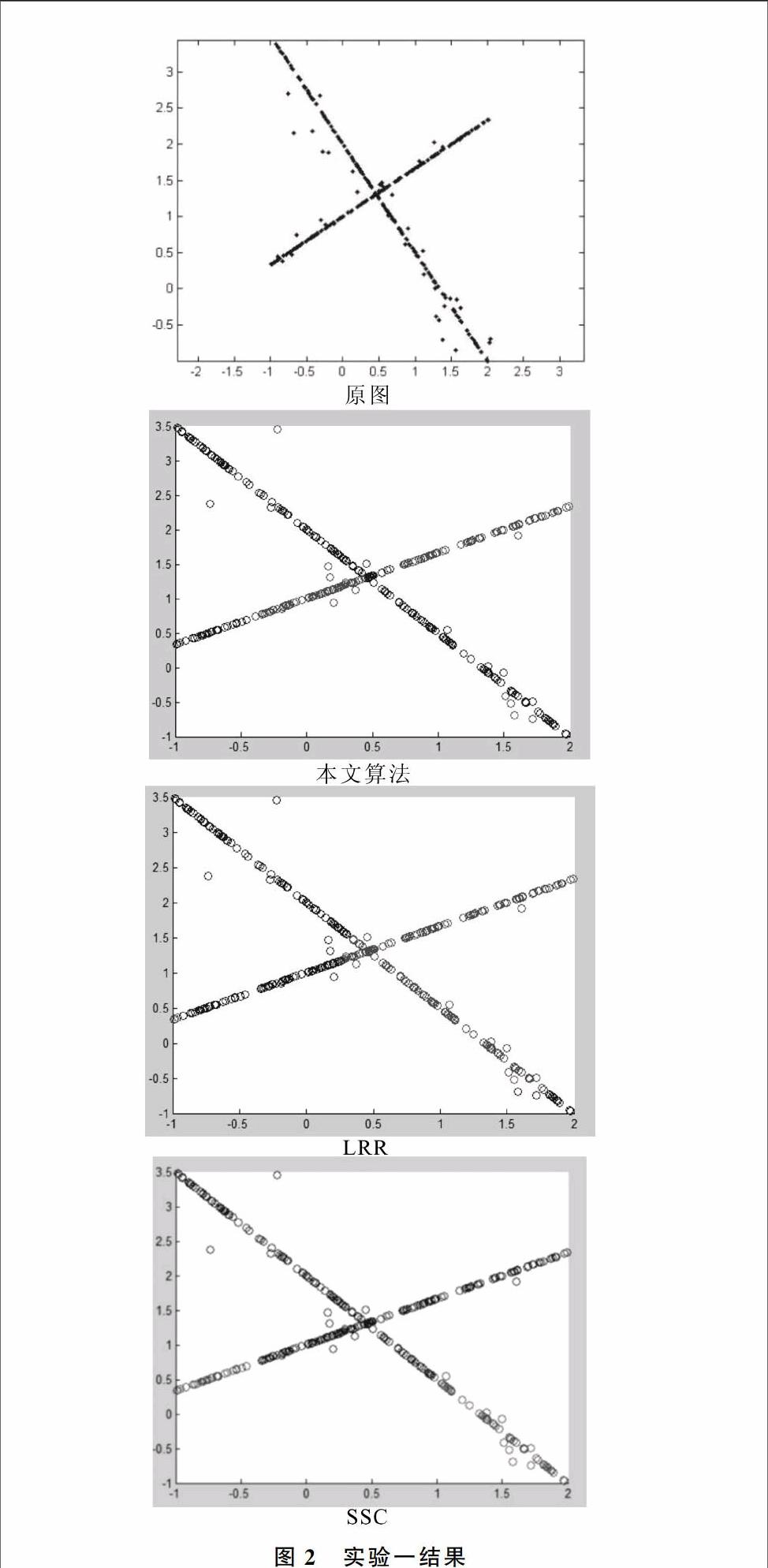
从图2可以看出，对分布在独立子空间中的两条直线上的数据进行聚类，若每条直线上的数据为一类，则本文提出方法的聚类结果明显要比LRR和SSC好。LRR和SSC算法聚类效果欠佳的原因在于对数据分解处理后用K-means算法[8]进行聚类，K-means算法以距离度量为基础，适合于发现球状簇，对于线性数据的聚类效果并不理想。本文算法和LRR算法的主要误差都在于图像交叉相似的部分，但LRR算法的聚类误差部分明显大于本文算法的聚类误差部分，而SSC算法基本无法聚类该图数据。

3结语

本文提出一种基于变化率聚类的算法，首先观察数据，按属性重要性筛选出的维对不同结构数据进行分类，然后在同构数据点之间按其变化率进行分类，若变化率超过一定的阈值β，则分到不同的类中；若小于或等于β，则分到同一类，最终得到各个不同结构的分类。此算法能够有效对低维多流形非相似结构的数据进行聚类分析，聚类效果明显优于LRR、SSC等传统算法，且时间复杂度较低，可以进一步应用到图像分类、运动识别等领域。

参考文献：

[1]JB TENENBAUM，VD SILVA，JC LANGFORD.A global geometric framework for nonlinear dimensionality reduction[J].Science，2000，290（5500）：23192323.

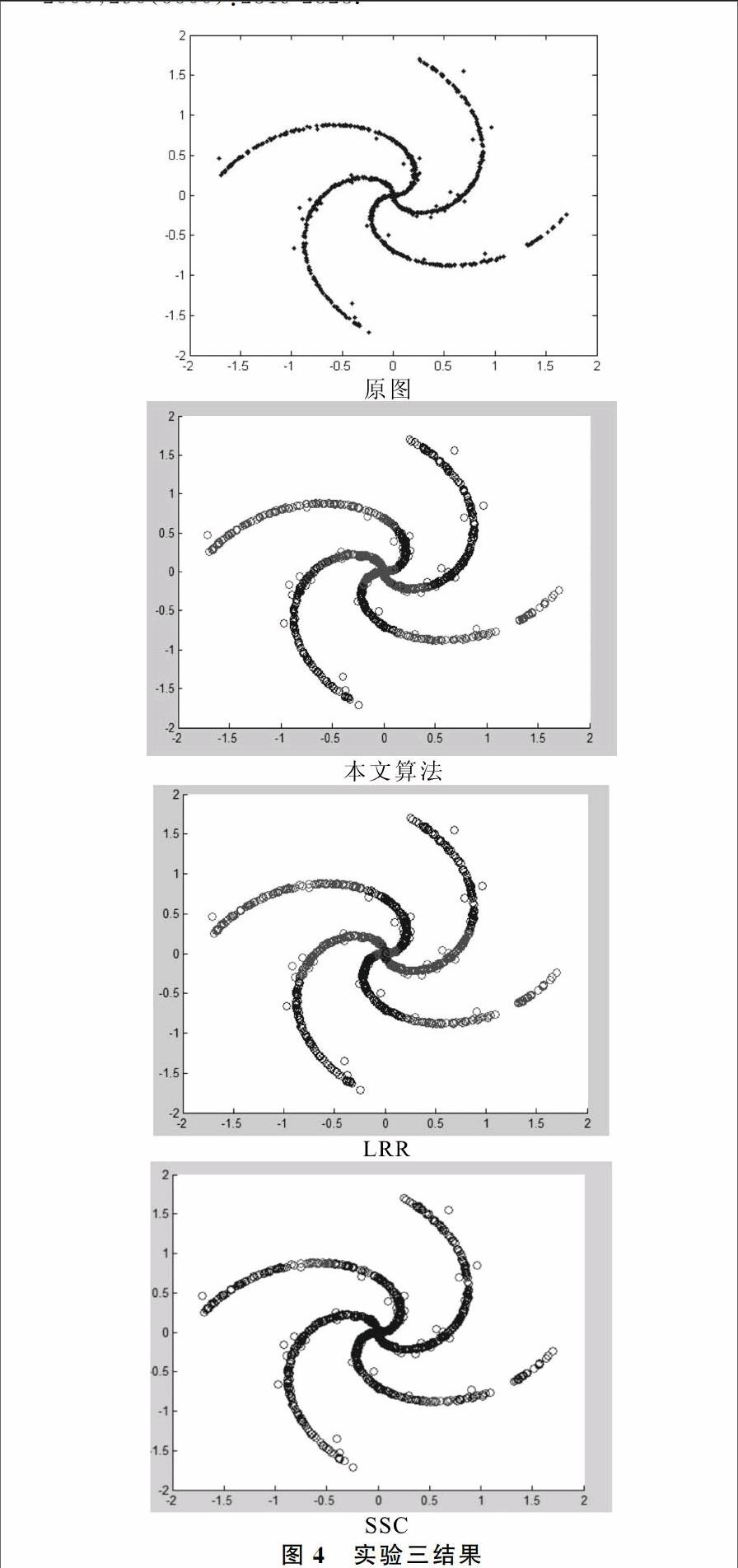
图4实验三结果

[2]E ELHAMIFAR，R VIDAL.Sparse subspace clustering[C].IEEE Conference on Computer Vision and Pattern Recognition，2009：27902797.

[3]郑媛媛.基于非负矩阵分解的数据表示算法研究及其应用[D].南京：南京理工大学，2013.

[4]J SHI，J MALIK.Normalized cuts and image segmentation[J].IEEE Transactions Pattern Analysis Machine Intelligence，2000，22（8）：888905.

[5]G LIU，Z LIN，S YAN，et al.Robust recovery of subspace structures by lowrank representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2013，35（1）：171184.

[6]E ELHAMIFAR，R VIDAL.Sparse subspace clustering：algorithm，theory，and applications[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2013，35（11）：27652781.

[7]王衛卫，李小平，冯象初，等.稀疏子空间聚类综述[J].自动化学报，2015，41（8）：13731384.

[8]周爱武，于亚飞.KMeans聚类算法的研究[J].计算机技术与发展，2011，21（2）：6265.