舰载武器控制台动力学分析及优化设计

焦冀光 杨 春 庄锦程 刘文一

(1.91550部队91分队 大连 116023)(2.北京宇航系统工程研究所 北京 100076)

舰载武器控制台动力学分析及优化设计

焦冀光1杨 春2庄锦程1刘文一1

(1.91550部队91分队 大连 116023)(2.北京宇航系统工程研究所 北京 100076)

为了研究舰船振动对安装在其上的武器控制台的影响,建立了武器控制台有限元模型,对武控台空柜和大质量仪器安装在武控台不同位置时进行了模态分析和频率响应分析。结果表明:大质量仪器的安装会改变武控台动力学特性,安装位置不合理会导致武控台与舰船发生共振产生超出设计值的变形位移。

武器控制台; 舰船; 模态; 频率响应

Class Number E92

1 引言

舰船在航行过程会在风浪的作用下晃动,表现为低频高幅振动,这个振动会传递到安装在舰船上的各个设备。舰载武控台由于其高宽/深比大,分层多,且内部安装有重要仪器,使得其对振动载荷较为敏感。如果舰载武器控制台的抗振能力差,又没有采取抗振措施,舰载武器控制台就会在这些载荷的作用下受损,从而导致舰船失去作战能力[1]。

武控台内部一般都有隔板,用来安装各种的设备,设备安装位置不同会使武控台动力学特性发生变化,为了研究仪器在武控台不同位置时的动力学特性和在外载荷作用下的响应,有必要对其进行动力学特性分析。

2 武控台模型

某型舰载武器控制台壳体为铸铝,设计有三层隔板用来安装仪器,隔板用螺栓固联在柜体上,有一台重达26kg的仪器需安装在这三层隔板或者底板上。

计算中划分实体单元,使用IsoMesh划分器,共划分3626个单元。隔板与柜体之间采用Connector联接方式,用Fastener使两者之间的节点联接[2]。在设计安装26kg的仪器的位置划分0维单元,然后将26kg作为集中质量,平均分布在这些单元上。柜体底部四角和后背板通过减振器与舰体联接,其中柜体底部约束其x和y方向的自由度,而背板联接点则约束其x和z方向自由度,计算有限元模型如图1所示。

图1 武控台有限元模型

3 计算模型

3.1 模态分析

模态分析主要任务是求解固有频率和振型,而固有频率和振型的计算是一个特征值问题,特征值对应固有频率,特征向量对应振型。阻尼及外加载荷均为0的情况下,系统的自由振动方程的矩阵形式为

(1)

式中:[M]为质量矩阵;[K]为刚度矩阵。

对于线性结构系统,[M]和[K]均为实对称阵,方程(1)有简谐函数形式的解:

{u}={φ}sinωt

(2)

式中{u}为特征向量或振型;ω为圆频率。

将{u}及其微分代入式(2),得到下式:

-ω2[M]{φ}sinωt+[K]{φ}sinωt=0

(3)

上式在任意时刻t均成立,故可简化为

([K]-ω2[M]){φ}=0

(4)

这是典型的特征值问题。上式{φ}有非零解的条件是:([K]-ω2[M])是奇异的,即矩阵系数的行列式为

det([K]-ω2[M])=0

(5)

或:

det([K]-λ[M])=0

(6)

式中:λ=ω2。

(7)

每个特征值和特征向量决定结构的一种自由振动形式。特征值与特征向量的数目与动力自由度的数目相同[3]。

用式(7)求解{φi}相当于求解一组联立方程组。由于([K]-ω2[M])是奇异的,故此联立方程组为线性相关的,{φi}有无限组解,即{φi}的矢量方向是一定的,但大小可以任意。这意味着振型的振幅是任意的,但振型的形状是唯一的。为了便于识别,须将特征向量正规化至适当的大小。质量正规化方法是特征向量正规化的默认方法,它调整特征向量个分量的值使广义质量矩阵等于1,即:

{φi}T[M]{φi}=1

(8)

当一个线弹性结构在自由或强迫振动下振动时,它在任意时刻的振动形状是所有模态的线性组合,即:

(9)

需要注意的是一个特征值问题只能确定特征向量的方向,而不能确定其绝对长度。事实上,对于振动问题,说模态向量的方向是由系统的参数与特性所确定的,即它的振型形状是确定的,而振型的“长度”,即振幅的大小,却不能由特征值问题本身,即不能由运动方程给出惟一的答案,利用有限元分析技术,则可求解出系统振型[4]。

3.2 频率响应分析

频率响应分析是用来计算结构在振动激励下响应的方法。在频率响应分析中,根据外载荷频率求解耦合的运动方程;当使用模态阻尼或无阻尼时,模态法利用结构的振型缩简和解耦运动方程,对各个模态响应进行迭加得到一特定外在频率的解[5]。

(10)

对简谐运动,假定一个简谐形式的解:

{x}={u(ω)}eiωt

(11)

式中{u(ω)}为复位移向量。

将位移表达式(11)求一阶和二阶导数带入式(10)得到:

-ω2[M]{u(ω)}eiωt+iω[B]{u(ω)}eiωt
+[K]{u(ω)}eiωt={p(ω)}eiωt

(12)

上式简化得到:

[-ω2M+iωB+K]{u(ω)}={p(ω)}

(13)

如果考虑阻尼或外载有相位角,则此表达式代表复系数方程系统。利用复数算法,对于每一个输入激励频率的运动方程,可以像静力问题类似地求解。结构的其他响应都可以通过位移向量求出[6]。

4 计算结果及分析

4.1 模态分析

对武控台空柜状态、大质量仪器安装在第一层(底板)、第二层、第三层和第四层时进行了模态分析,得到了模态振型和模态频率,如图2和图3所示。

图2 武控台各状态模态频率

图3 武控台各状态模态振型位移

从图2可以看出,大质量仪器无论安装在武控台任何一层,均减小了武控台的模态频率;大质量仪器安装在第二层时,前八阶模态频率最低,而安装在第四层时,前八阶模态频率较高,大质量仪器安装在第一层和第三层时,前十阶模态频率相差不大[7]。

语音研究应该采用相对化和归一化的数据，而非绝对的数据。（石锋，王萍2006）据此得到的研究结果才会有普遍的意义。因此，声调分析全部采用相对归一的T值计算（石锋1990），声调T值的计算公式如下：

从图3看出,空柜的第二、四和六阶模态振型位移较大,在第六阶模态时最大值达到了0.0653m;大质量仪器安装在一层、二层或四层时,振型位移在第九阶模态时振型位移最大,其值分别为0.0575m、0.0521m和0.0659m;而仪器安装在三层时,振型位移在第十阶模态时最大,其值为0.0703m。

各状态最大振型云图见图4。空柜状态最大振型位移发生在第一层;大质量仪器安装在第一层、第三层和第四层时,最大振型位移发生在第三层;而当大质量仪器安装在第二层时,最大振型位移发生在第四层。

图4 武控台各状态模态振型

4.2 频率响应分析

根据文献[8],舰船振动频率一般在5Hz～80Hz之间,舰载武控台会在这个振动载荷下发生振动,若武控台某阶模态频率与舰船振动频率相同,则武控台会与舰船发生共振,共振时会产生较大变形位移,若这个位移量超过允许值,则会使武控台破坏失效[9]。分析了武控台在空置状态,仪器分别安装在第一层、第二层、第三层和第四层时的频率响应,计算时取激振频率为0Hz～200Hz,得到了频率响应位移曲线。

(a)空柜

(b)仪器在一层

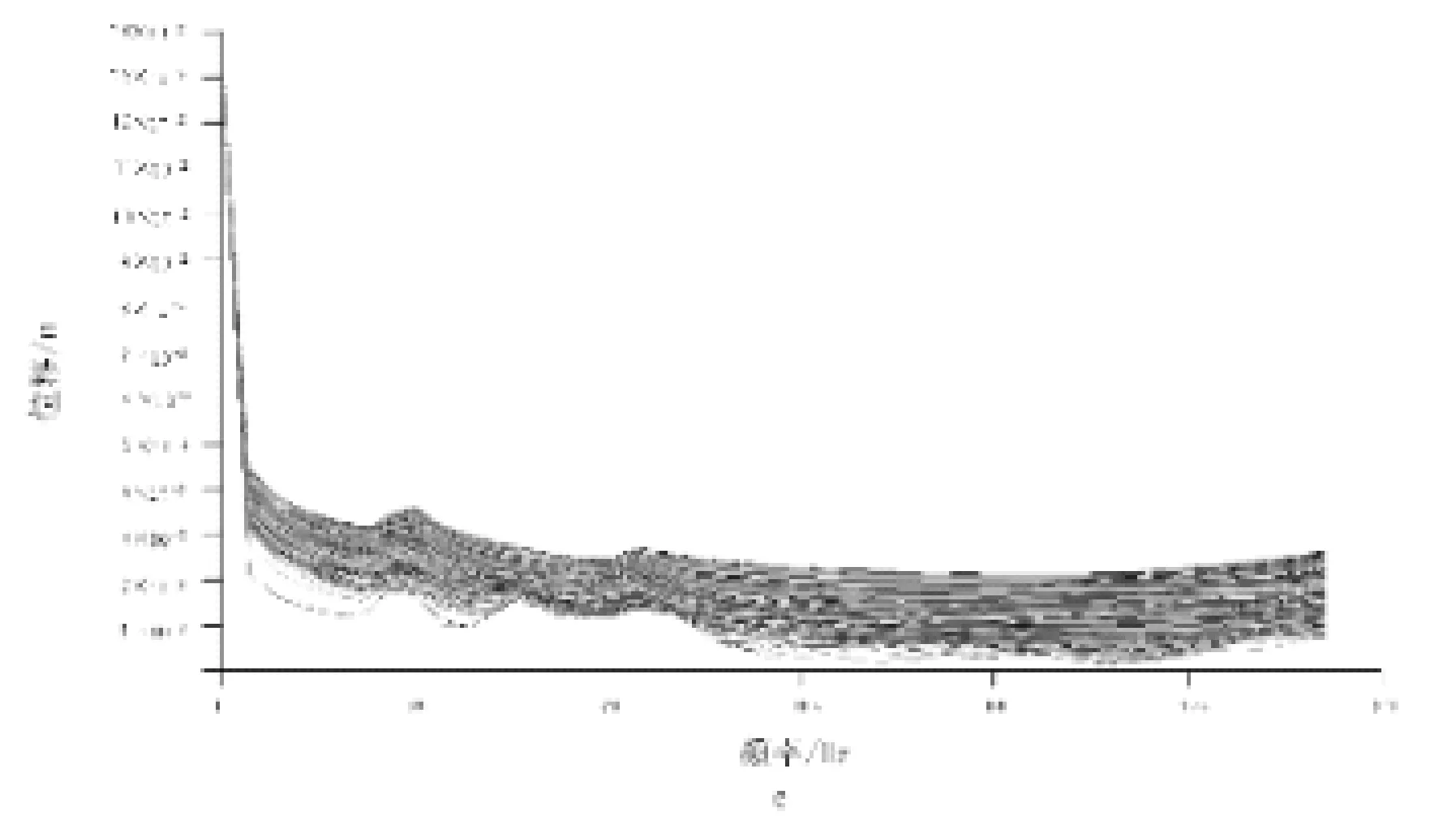
(c)仪器在二层

(d)仪器在三层

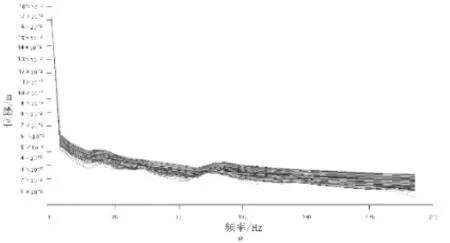
(e)仪器在四层图5 武控台各状态频响位移曲线

从图5可以看出,在舰船振动激励下,武控台发生了振动,振动时产生的最大位移如表1所示。

武控台空柜状态时振动位移最大,其值分布在3.4×10-2～7.5×10-2m之间,超过了设计允许值,但这种情况不会发生。

当仪器安装在第二层发生最大位移时,激振频率为40.3Hz,与其第二阶模态频率41.26Hz吻合;当仪器安装在第四层发生最大位移时,激振频率为27Hz,与其第一阶模态频率27.3Hz吻合,可认为在这两种状态下,武控台与舰船发生了共振[10]。

而仪器安装在第一层和第三层时,在舰船振动激励下发生最大位移时,激励频率均不在其任何一阶模态处,可认为仪器在这两种状态下不会与舰船发生共振。而仪器安装在第三层时,其频率响应位移值整体上均比仪器安装在第一层时大,因此将仪器安装在第一层较为合理。

表1 武控台各状态振动时最大位移

5 结语

根据舰船工作环境,建立了某型武器控制台有限元模型,对其在空柜状态和大质量仪器安装位置不同状态时进行了模态分析,获得了固有频率和相应的各阶振型。针对舰船摇摆振动,分析了武控台各状态频率响,获得了频率响应位移曲线,得出以下结论:

1) 大质量仪器安装在任何一层,均可减小武控台模态频率,但安装在第一层和第四层时,模态频率差别较大;

2) 大质量仪器的安装,减少了较大模态振型出现的阶次,使其从空柜状态时的三次减少为安装后的一次;

3) 在舰船摇摆振动的激励下,武控台在大质量仪器安装在第二层时在其第二阶模态处发生了共振,大质量仪器安装在第四层时在其第一阶模态处发生了共振,武控台与舰船发生共振时会出现较大变形位移,这个位移超过了设计值;

4) 大质量仪器安装在第一层和第三层时,武控台不会与舰船发生共振,且仪器安装在第一层时其频率响应位移值小于仪器安装在第三层,因此将仪器安装在第一层较为合理。

[1] 程林风,王敏毅,黄朝学.基于ANSYS的舰载电子机柜振动可靠性研究[J].四川兵工学报,2014,35(1):32-33.

[2] 刘文一.焦冀光.某飞行器复合材料薄壁加筋结构舱段稳定性分析[J].舰船电子工程,2016,36(1):21-23.

[3] 刘胜,荆兆寿.高海情下船舶减摇控制系统的仿真[J].船舶工程,1995(2):37-41.

[4] 邱成悌,赵惇殳,蒋全兴,等.电子设备结构设计原理[M].南京:东南大学出版社,2002:16-18.

[5] 袁东红.舰载电子设备抗冲击设计概要[J].噪声与振动控制,2013,36(6):2-3.

[6] 程林风,王敏毅,黄朝学.基于ANSYS的舰载电子机柜振动可靠性研究[J].四川兵工学报,2014,35(1):6-8.

[7] 龙凯,贾长治,李宝峰,等.Patran2010与Nastran2010有限元分析从入门到精通[M].北京:机械工业出版社,2011:76-83.

[8] 董见.罗建新.甚低频气球天线缆绳末端损耗及温升分析[J].舰船电子工程,2015,35(12):159-161

[9] 张仪,陈曦.武器装备试验仿真系统可信度评估指标研究[J].舰船电子工程,2015,35(10):136-138.

[10] 张登,徐宏斌,张大治,等.基于ADAMS的某型发射装置燃气解锁机构运动学仿真分析[J].弹箭与制导学报,2016(3):11-14

Dynamics Analysis and Optimum Design Optimization of Shipboard Weapons Control Cabinet

JIAO Jiguang1YANG Chun2ZHUANG Jingcheng1LIU Wenyi1

(1. Unit 91, No. 91550 Troops of PLA, Dalian 116023) (2. Beijing Institute of Astronautical System Engineering, Beijing 100076)

A finite-element model was established to research the effect of vibration of shipboard weapons control cabinets, modal and frequency response were analyzed when the weapons control cabinet was empty and when a heavy equipment was assembled on the different baffle of weapons control cabinet. It proved that when the heavy equipment was assemblyed on the different baffle, its dynamics characteristic would be changed, if the heavy equipment was assembled on the irrational location, the resonance would be generated between weapons control cabinet and ship, and the large displacement would be generated which beyond the design value.

weapons control cabinet, ship, modal, frequency response

2016年8月12日,

2016年9月26日

焦冀光,女,助理工程师,研究方向:武器控制工程。杨春,男,硕士,高级工程师,研究方向:导弹动力系统总体。庄锦程,男,高级工程师,研究方向:武器控制工程。刘文一,男,硕士,工程师,研究方向:导弹动力系统。

E92

10.3969/j.issn.1672-9730.2017.02.036