基于LQR变传动比控制的4WIS电动车转向控制仿真研究*

董铸荣,张 欣,胡松华,邱 浩

(1.北京交通大学机电控制工程学院,北京 100044; 2.深圳职业技术学院汽车与交通学院,深圳 518055)

基于LQR变传动比控制的4WIS电动车转向控制仿真研究*

董铸荣1,2,张 欣1,胡松华2,邱 浩2

(1.北京交通大学机电控制工程学院,北京 100044; 2.深圳职业技术学院汽车与交通学院,深圳 518055)

理想转向特性对改善车辆操纵稳定性有重要意义。本文中基于LQR最优控制理论,提出了一种新型后轮主动转向变传动比控制策略。首先,综合考虑低速操纵响应性与高速行驶稳定性,建立4WIS电动车理想转向特性;接着根据变传动比曲线设计预期的横摆角速度,并基于LQR最优控制理论提出了主动后轮转向控制策略,以跟踪横摆角速度的预期值;最后,针对典型的双移线工况,进行人车路闭环控制仿真,结果表明,所提出的控制策略较好地实现了理想转向特性。

4WIS电动车;转向控制;LQR;变传动比;闭环仿真

前言

现代汽车越来越多采用四轮转向(4WS)系统来改善汽车的操纵稳定性。现有的4WS汽车大多采用前轮转向机构不变、后轮主动转向的方式,许多有关后轮主动控制策略方面的新理论被提出,如零滑移角比例控制[1]、零滑移角μ综合控制[2]、横摆角与滑移角解耦控制[3]和多目标横摆角速度跟踪控制[4]等。现有理论多采用零质心侧偏角的控制策略,它存在横摆角速度增益小,高速时转向不足过大的缺点。采用横摆角速度跟踪的控制策略,其跟踪的期望横摆角速度是由采用固定传动比的前轮转向求得,结果不能保证获得较为理想的转向特性。另外,在控制理论方面,许多学者将LQR方法应用于两轮自平衡电动车、四轮驱动电动车的稳定性控制中[5-6],取得了较好的效果。

理想的转向特性要求汽车在低速下具有高的转向灵敏性和高速下具有好的转向稳定性,这对传统的采用固定传动比的前轮转向汽车来说很难满足要求。为此,本文中针对自行开发的四轮独立驱动独立转向(4WID-4WIS)电动车采用变传动比来满足上述要求[7]。由于变传动比转向系统的机械结构复杂、成本高,本文中基于LQR最优控制方法提出了汽车后轮主动转向控制策略,并考虑驾驶员模型设计了人车路闭环仿真试验,实现了汽车的变传动比跟踪,使其获得理想的转向特性。该方法可在不改变前轮转向结构的情况下,通过调整后轮获得变传动比的理想转向特性,大大降低了设计成本,避免了机械结构的限制。

1 车辆横向动力学模型

为更好地研究四轮独立转向电动车的横向动力学,采用简化的2自由度车辆模型[8],如图1所示,不考虑车辆侧倾的影响,车速恒定。其中,γ为横摆角速度,β为滑移角,δf和δr为前后轮转角,αf和αr为前后轮侧偏角,lf和lr为质心到前后轴距离,L为轴距,v为车速,vf和vr为前后轮速,Fyf和Fyr为前后轮侧向力。

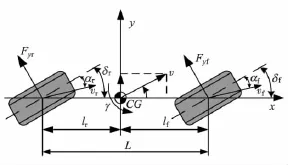
图1 线性2自由度车辆模型

由模型得四轮转向车辆模型的运动方程为

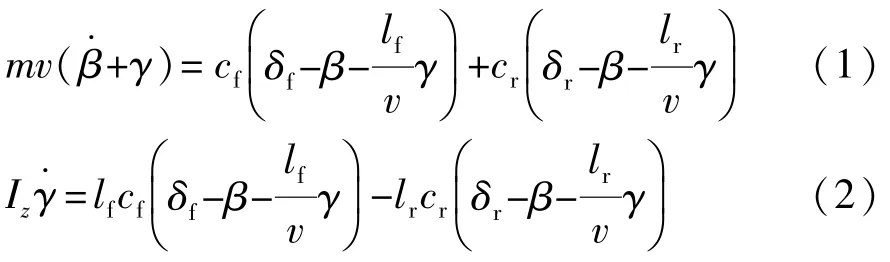
式中:m为整车质量;Iz为整车横摆转动惯量;cf为前轴侧偏刚度;cr为后轴侧偏刚度。

取状态量x=[β γ]T,输出量y=[β γ]T,则由式(1)可得状态方程:

其中:

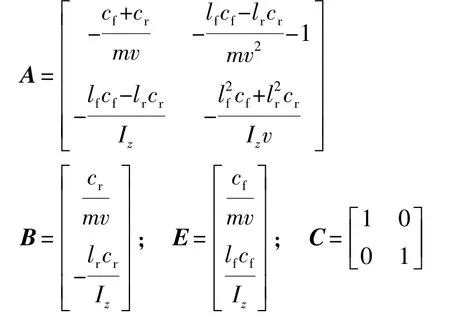
本文中研究对象的整车和轮胎关键参数见表1。

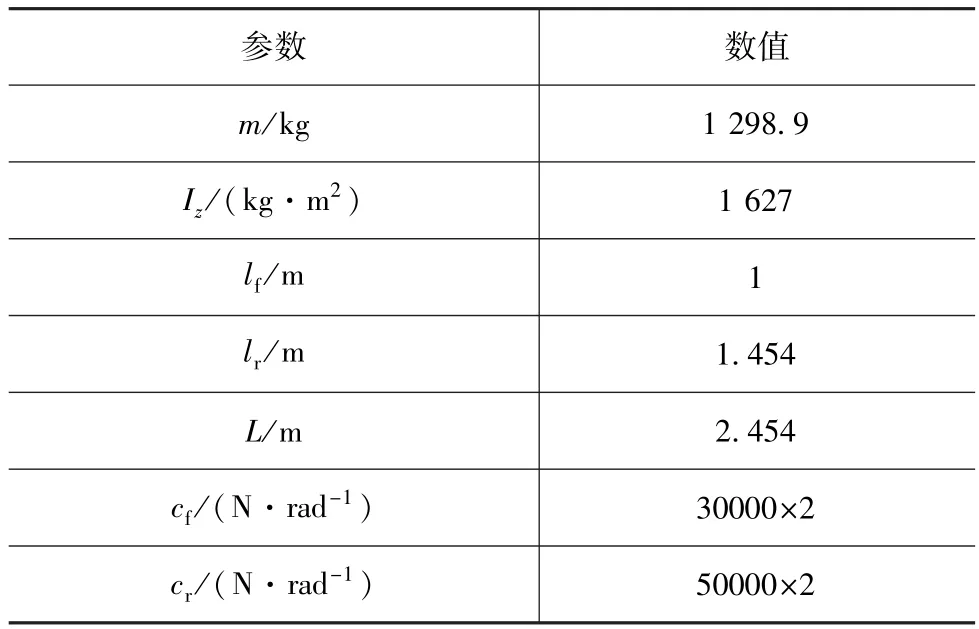
表1 车辆和轮胎参数

2 转向控制策略

基于LQR最优控制方法,建立变传动比的理想模型,提出一种变传动比控制策略。

2.1 LQR最优控制

线性动态系统求最优解的问题通常被称为线性二次型问题,它有2个特点:(1)相对于其他最优控制研究对象为单输入单输出系统,线性二次型所研究目标为多输入多输出系统的最优控制问题;(2)目标系统性能指标相比其他最优控制更加综合、灵活和实用。

线性二次型调节器的控制目标是使系统的实际输出y(t)能跟随期望输出yr(t),即寻找最优控制u*(t),使系统的实际输出y(t)在确定的时间间隔[t0,tf]内尽量接近预期的输出。

设线性时变系统的状态空间表达式为

定义误差矢量为

性能指标J为

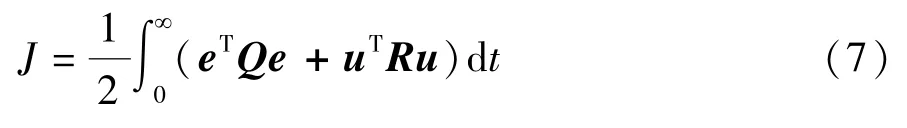
式中:Q和R为正定对称时变矩阵。

为使J最小,引入拉格朗日乘子矢量λ,构成哈密尔顿函数:

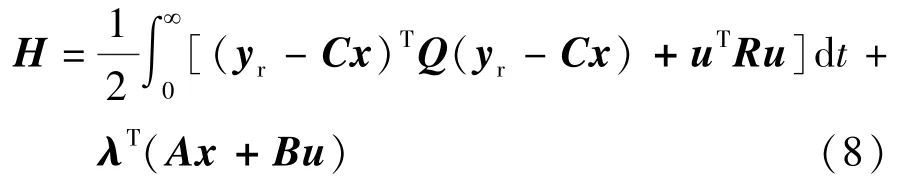
最优控制目标是H取得极小值,即

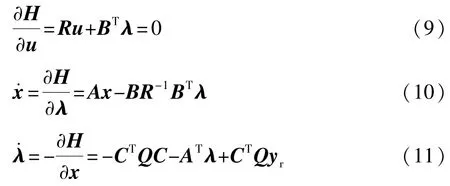
经过推导可得最优控制为

式中:P为对称正定常数矩阵;g为常值伴随矩阵,满足方程:

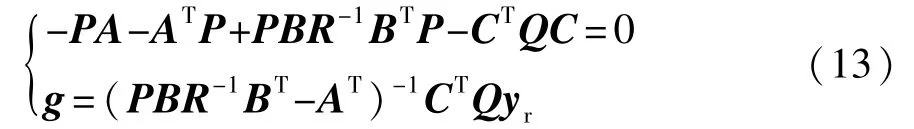
式(13)表明,线性调节器LQR问题的解是全部状态变量的最优线性负反馈,因此本文中将LQR方法应用于四轮独立电动车的变传动比控制中。

2.2 变传动比车辆理想模型

控制系统理想模型的设计应以物理系统为基础,通常情况下,四轮转向时驾驶员的期望驾驶感受应与前轮转向汽车相同,也即如果不考虑汽车横摆角速度对前轮输入响应的瞬态影响,车辆转向稳态响应作为唯一考虑因素,则四轮转向理想横摆角速度即可用相同参数的前轮转向车辆横摆角速度稳态值来代替。

汽车等速行驶时,固定传动比前轮转向的前轮转角为式中:θsw为转向盘转角;i为转向盘转角与前轮转向角的传动比。

将车身和悬架视为刚体,则质心处的横向加速度ay[9]为

稳态期望横摆角速度为

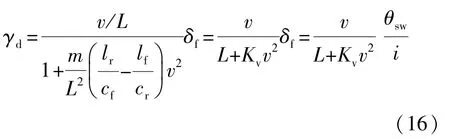
其中:

式中Kv一般称为稳定性因素,是影响汽车稳态性能的重要参数。

对于具有理想转向特性的汽车来说,其期望横摆角速度应随车速的增加而降低,在低速时具有大的转向增益,高速时具有小的转向增益,如图2所示。但传统的定转向传动比机构无法满足上述要求。为此,采用变传动比求期望横摆角速度。

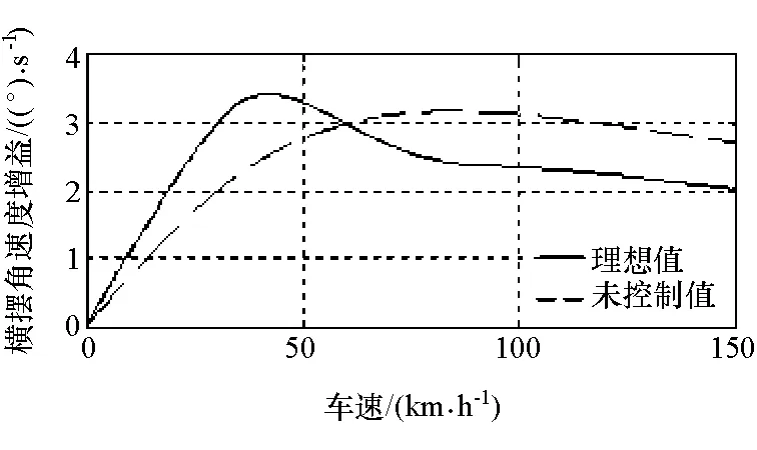
图2 不同车速下的横摆角速度增益曲线

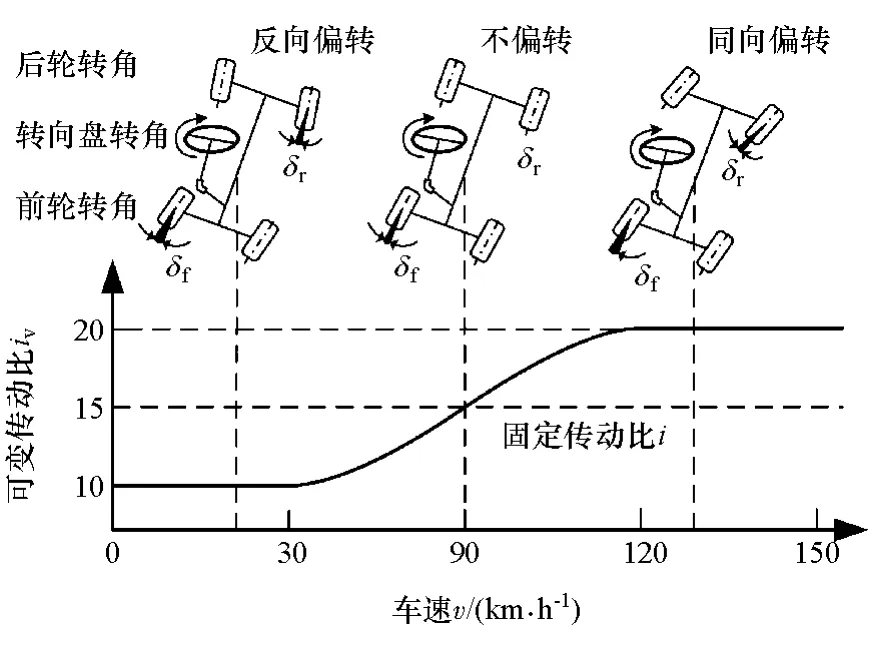
图3 不同车速下的变转向传动比曲线

变传动比能够为驾驶员提供良好的操纵稳定性。本文中采用的变传动比iv运动学函数与车速有关,如图3所示[9]。中低速时,iv较小,大幅度减小驾驶员的转向任务,转向更加直接、轻便;高速时,iv较大,增加驾驶员的转向任务,转向较为沉重,从而提高方向稳定性。

为获得理想转向特性,可通过采用变传动比来获得期望的横摆角速度,即式(16)中的定传动比i可用变传动比 iv替代,则期望横摆角速度γd为

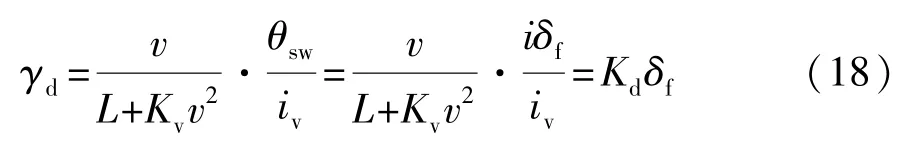
2.3 主动后轮转向LQR控制器

与传统的两轮转向汽车相比,4WIS汽车更容易获得期望的操纵性能。若理想的转向特性已知,可采用全速度跟踪的方法来实现理想的转向特性。为提高汽车的低速机动性和高速操纵稳定性,采用LQR最优控制方法设计4WIS控制器,用于跟踪期望横摆角速度γd。图4为控制器结构,转动转向盘时,采用调整后轮转角的方式,使实际的横摆角速度跟踪期望的横摆角速度。

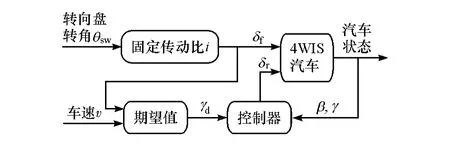
图4 基于理想横摆角速度跟踪的4WIS控制系统

状态方程的控制输入为后轮转角,干扰输入为前轮转角,则式(3)可写为

其中:u(t)=δr;y(t)=γ(t)

定义输出误差e(t)=yd(t)-y(t),其中yd(t)= γd(t)。根据LQR最优控制理论,上述跟踪问题则变为求取控制输入u(t),使性能指标J极小。

根据式(7),并应用LQR理论进行推导,最终可求出后轮控制器(见图5):

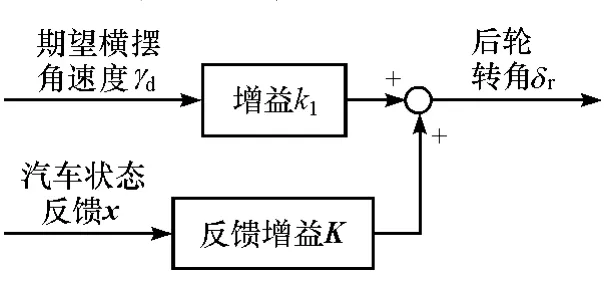
图5 控制器的控制策略

其中:

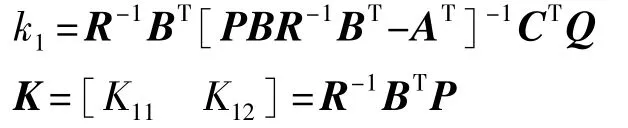
式中:k1为期望横摆角速度增益;K为汽车状态变量的反馈增益。

综合式(3)、式(13)、式(19)和式(20),得到前、后轮转角的关系式为

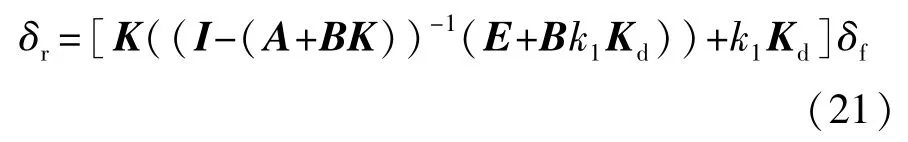
3 仿真与分析

运用Matlab/Simulink软件对上述4WIS控制算法进行仿真,并将结果与固定传动比控制进行对比。

3.1 闭环控制仿真设计

为真实地反应该控制策略的效果,搭建人车路闭环控制系统,如图6所示,用于控制系统的闭环仿真研究。其中驾驶员模型采用郭孔辉院士的最优预瞄侧向加速度驾驶员模型[10]。

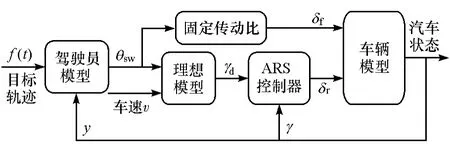
图6 基于主动后轮转向控制的闭环控制系统

仿真工况选为典型的双移线工况,用于模拟车辆在实际道路上进行的超车或紧急避障情况,路径设置情况如图7所示。

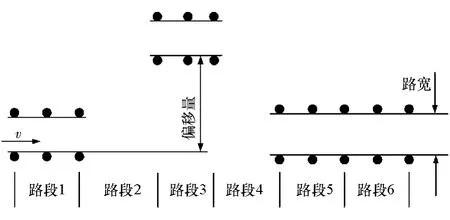
图7 双移线路径设置

图中的圆点代表桩桶,相应的路径参数和偏移量如表2所示。

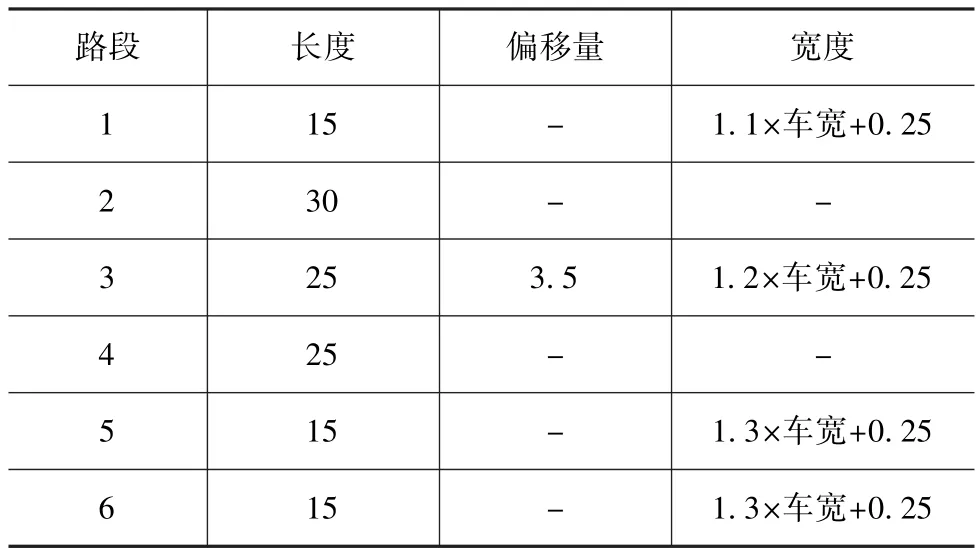
表2 双移线路径参数 m

在进行双移线目标轨迹的路径规划时,路段1、路段3、路段5和路段6采用桩桶中心直线,而路段2和路段4采用多项式拟合曲线,确保曲线段和直线段能够光滑连接。X表示纵向位移,Y表示横向位移,采用拟合多项式表达双移线目标轨迹:

可根据连接点的约束条件,求取多项式的各项系数,进而确定经过光滑拟合后的双移线目标轨迹。为便于观察仿真结果,在标准路径前额外加了50m,在标准路径后额外加了75m,如图8所示。

为充分验证控制器的有效性,分别进行低速(10m/s)、中速(20m/s)和高速(30m/s)的仿真,路面附着系数为0.85,对比仿真“无控制”、“固定传动比”和“变传动比”3种情况。

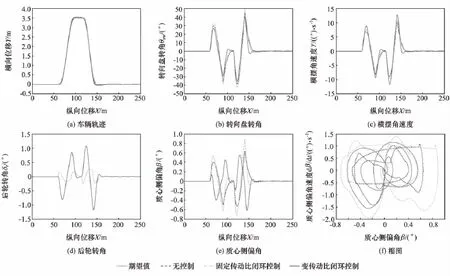
图9 低速闭环仿真结果

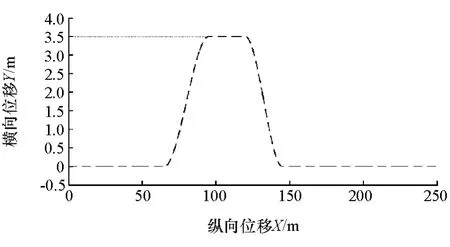
图8 双移线目标轨迹

3.2 仿真结果与分析

3.2.1 低速(10m/s)

低速闭环仿真结果如图9所示。由图9(a)可见,当车辆以低速行驶在良好路面上时,3种控制系统都能很好地实现目标轨迹的跟踪。但由图9(b)可见,变传动比控制系统的转向盘转角小于固定传动比控制系统,这与前期的设计思路相符,即低速采用小传动比以提高系统的操纵性,降低转向盘转角,使驾驶员响应更加及时。由图9(c)可见,变传动比系统的横摆角速度大于固定传动比系统,原因是采用小的传动比提升了系统的增益,符合前期设计思路。由图9(d)可见,变传动比系统的后轮转角大于固定传动比系统,这是由于变传动比系统需求的横摆角速度增益较大造成的。由图9(e)和图9(f)可见,变传动比系统的稳定性要高于固定传动比系统。

3.2.2 中速(20m/s)

中速闭环仿真结果如图10所示。由图10(a)可见,当车辆以中速行驶在良好路面上时,3种控制系统都能够较好地实现目标轨迹的跟踪。但由图10(b)和图10(c)可见,无控制系统的转向盘转角和横摆角速度出现了较大波动,而固定传动比系统和变传动比系统的波动较小,其中变传动比系统的横摆角速度控制最好。由图10(d)可见,变传动比系统的后轮转角大于固定传动比系统,这是为了使变传动比系统的质心侧偏角不至于过大造成的,如图10(e)所示。同时,由图10(f)可见,变传动比系统的相图范围小于固定传动比,这意味着变传动比系统与固定传动比相比,变传动比系统提高了车辆系统的稳定性。

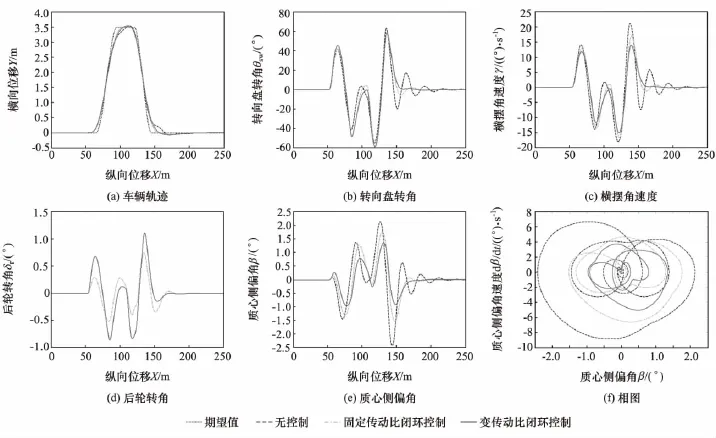
图10 中速闭环仿真结果

3.2.3 高速(30m/s)

高速闭环仿真结果如图11所示。当车辆以高速行驶在良好路面上时,无控制系统出现跑偏情况,车辆质心侧偏角过大,系统已经出现失稳,如图11 (e)所示。由图11(b)可见,变传动比系统的转向盘转向大于固定传动比系统,这与前期的设计思路相符,即高速情况下,降低系统的增益,增加转向盘转角。由图11(c)可见,变传动比系统的横摆角速度略小于固定传动比,同时,横摆角速度实现较为光滑的过渡。由图11(d)和图11(e)可见,变传动比系统的后轮转角大于固定传动比系统,这是为了限制变传动比系统的质心侧偏角。由图11(f)可见,变传动比系统的相图范围明显小于无控制系统,这意味着本文中设计的变传动比系统能够有效提高车辆系统的稳定性,同时,也使驾驶员获得理想的车辆转向特性。

上述阶跃特性闭环仿真结果表明,与前轮转向控制相比,本文中所提出的基于LQR的主动后轮转向变传动比控制策略可满足理想特性的要求,既能有效提高车辆系统的稳定性,又能使驾驶员获得较为理想的车辆转向特性,即中低速转向时,提高稳态横摆角速度,确保了低速时车辆转向轻便;车辆高速转向时,显著降低质心侧偏角,使转向沉重,确保良好的转向稳定性[11]。

4 结论

针对四轮独立驱动独立转向电动汽车的转向稳定性问题,运用LQR最优控制理论,建立了变传动比的理想模型,并提出了一种变传动比控制策略,通过仿真分析得到明确结论。

根据变传动比变化曲线设计能表征理想转向特性的期望横摆角速度,基于LQR最优控制理论,提出一种新型的主动后轮转向控制策略,以达到跟踪期望横摆角速度的目标,并进行人车路闭环控制的仿真。结果表明,该控制策略可在确保车辆稳定性的同时获得较为理想的转向特性,低速时通过较高的系统增益确保低速时转向轻便;高速时主动减小系统增益和质心侧偏角,使转向沉重,确保高速时的稳定性。

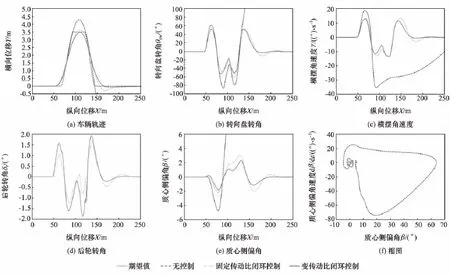
图11 高速闭环仿真结果

[1] NAGAI M,NISHIZAWA Y,TERANISHI K.Stability of 4WS vehicle based on side slip zeroing control:influence of steering system dynamics[C].In Proceedings of the 6th International Pacific Conference on Automotive Engineering,Seoul,1991,951-960.

[2] GAO X M,BRIAN D M,ROBERT L T.Robust controller design of four wheel steering systems using μ synthesis techniques[C].In Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans,1995,1,875-882.

[3] MARINO R,SCALZI S.Asymptotic sideslip angle and yaw rate decoupling control in four-wheel steering vehicles[J].Vehicle Syst.Dyn.,2010,48(9):999-1019.

[4] LV H M,CHEN N,LI P.Multi-objective H∞optimal control for four-wheel steering vehicle based on yaw rate tracking[J].Proc. Inst.Mech.Eng.,Part D:J.Automobile Eng,2004,218(10): 1117-1123.

[5] 胡建.两轮自平衡电动车的建模与控制研究[D].杭州:浙江大学,2014.

[6] 胡蕾蕾.电动汽车主动安全避撞控制系统研究[D].长春:吉林大学,2014.

[7] 徐正会,张元洪.车辆可变齿轮比转向系统之创新设计[C].台湾第19届机械工程研讨会论文集,2002,1.

[8] RAJAMANI R.Vehicle dynamics and control[M].Springer,New York,2005.

[9] KLIER W,REIMANN G,REINELT W.Concept and functionality of the active front steering system[C].SAE Paper 2004-21-0073.

[10] 郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社, 1991.

[11] 邱浩,雷正保,贺萍.基于变传动比的后轮主动转向控制方法研究[J].机械科学与技术,2015(1).

A Simulation Study on the Steering Control of a 4WIS EV Based on LQR Variable Transmission Ratio Control

Dong Zhurong1,2,Zhang Xin1,Hu Songhua2&Qiu Hao2
1.School of Mechanical,Electronic and Control Engineering,Beijing Jiaotong University,Beijing 100144; 2.School of Automotive&Transportation Engineering,Shenzhen Polytechnic,Shenzhen 518055

Ideal steering characteristics have important significance to the improvement of handling and stability of vehicle.In this paper,a novel variable transmission-ratio control strategy for rear-wheel active steering is proposed based on LQR optimal control theory.Firstly with concurrent considerations of low-speed handling responsiveness and high-speed driving stability,the ideal steering characteristics of a 4WIS electric vehicle are established.Then,the expected yaw rate is designed according to variable transmission-ratio curve,and by applying LQR optimal control theory,an active rear-wheel steering control strategy is proposed,so as to trace the expected values of yaw rate.Finally,a simulation on human-vehicle-road closed loop control under typical double lane change condition is conducted.The results show that with the control strategy proposed,the ideal steering characteristics can be well implemented.

4WIS-EV;steering control;LQR;variable transmission ratio;closed loop control simulation

10.19562/j.chinasae.qcgc.2017.01.013

*广东省自然科学基金(2016A030313024)、深圳市重点实验室(ZDSYS20160229100057381)和深圳市基础研究项目(JCYJ20140718171525577)资助。

原稿收到日期为2016年7月25日。

胡松华,博士,E-mail:husonghua@szpt.edu.cn。