一种基于矩阵的并行CRC校验算法

赵坤鹏，吴龙胜，马徐瀚，陈庆宇

（西安微电子技术研究所 陕西 西安710054）

一种基于矩阵的并行CRC校验算法

赵坤鹏，吴龙胜，马徐瀚，陈庆宇

（西安微电子技术研究所 陕西 西安710054）

针对高速网络通信中高位宽并行数据的实时校验需求，提出了一种可单周期实现的、面向128位并行数据的循环冗余校验算法（Cyclic Redundancy Check，CRC）。该算法首先根据CRC串行编码原理得到8位并行数据的CRC校验矩阵，之后对矩阵进行迭代简化，得到32位并行数据的参数矩阵，此参数矩阵作为该CRC算法的核心实现了对数据进行预处理。最后对该算法进行了硬件实现，仿真及综合结果表明，该算法可在单周期内完成对128位并行数据的CRC编码和解码校验，时钟频率提高1.8倍，而硬件开销仅增加5.15%。

128位并行数据；单周期；CRC算法；硬件实现；频率提高

为了保证通信系统中数据传输的可靠性，基于编解码的数据校验技术广泛应用，同时日渐提高的网络通信速率，迫切需要支持宽位并行数据的实时校验电路。

循环冗余校验码CRC作为编码校验中重要的编码方式，由于其易于硬件实现，具有良好的检错性能，在网络数据传输中得到广泛应用。CRC编码实现方式多样，有串行编码方式、查表法和公式法（也称推导法）。其中，串行编码只能处理串行数据，无法实现宽位并行数据校验[1]。查表法需要存储模块来存储表项，硬件消耗大，难以实现高位宽并行数据校验[2]。公式法在以太网和PCIe等高速并行通信中应用广泛，但其迭代推导方式对于高位宽数据（大于16）较为复杂。针对上述实现方法中存在的问题，文献[5]提出了基于级联结构的CRC校验方法，该方法电路结构清晰，可以实现对并行64位数据的校验，但随着并行数据位宽的提高，相应的链路延时会线性增长，无法实现高位宽（如128位）的实时校验。文献[6]提出了一种多通道并行CRC计算方法，其算法复杂，相应实现方式复杂，需要高性能处理器，硬件消耗较大，不适合应用于实际的专用集成电路中。文中提出了一种面向128位并行数据的CRC校验算法，该算法采用校验矩阵对128位数据进行了预处理，大大提高了宽位并行数据的校验效率。

文中首先介绍了当前CRC编码的研究现状，然后提出了一种针对宽位并行数据的CRC校验算法，该算法可以实现128位数据的单周期校验，并在此基础上对本文算法进行了硬件实现；之后，对硬件电路的功能和开销进行了仿真验证、综合分析；最后，对文中进行了总结。

1 CRC并行数据校验算法

传统的CRC-32校验是通过线性反馈移位寄存器（LFSR，Linear Feedback Shift Register）来实现的，如图1所示。

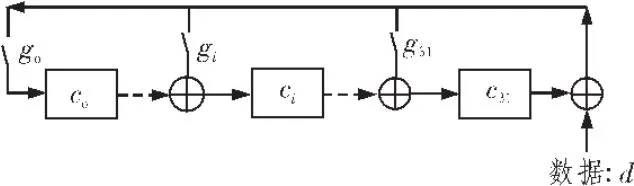
图1 LFSR结构框图

由此可知当前CRC值与当前数据输入和前一级CRC值的关系为

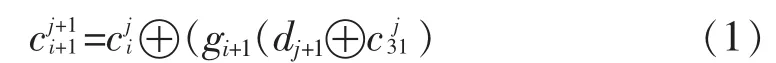
由式（1）的迭代关系可以递次推导出8位并行数据输入的当前CRC值与当前数据输入和8位数据输入之前的CRC值之间的关系，得到当前CRC值中每一位的值为：

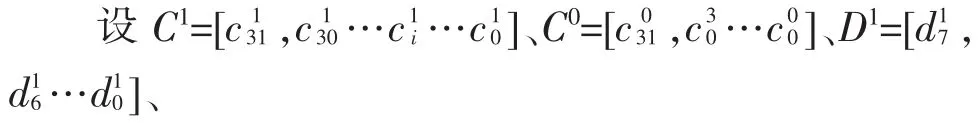
将式（2）中的异或由数学中的加号替代，则式（2）可表示为如下形式

由式（3）可以得到输入两次8位数据，即输入16位并行数据后的当前CRC值C2，如式（4），其中D2为第2次输入的8位数据。

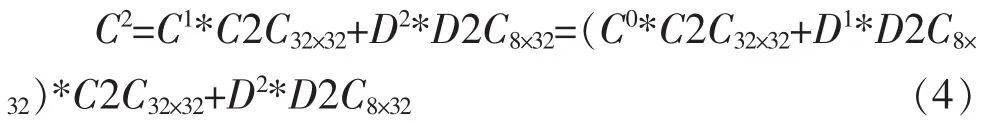
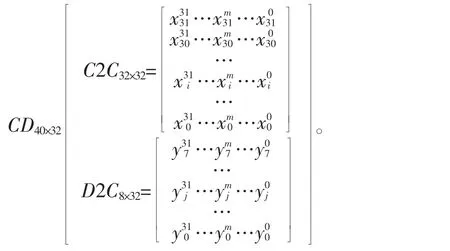
同理，继续迭代两次后得到输入4次8位数据，即输入32位并行数据后的CRC值

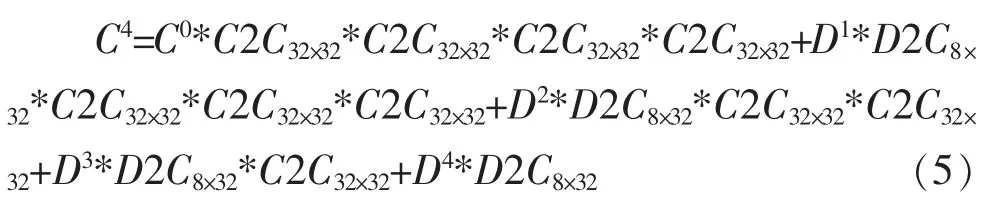
式（5）中的C0为前一级的CRC值，D1、D2、D3、D4分别为第一、二、三、四次输入的8位数据，为输入32位并行数据后的CRC值，C2C32×32*C2C32×32*

C2C32×32*C2C32×32为C0的参数矩阵，D2C8×32*C2C32×32* C2C32×32*C2C32×32为 D1的参数矩阵，D2C8×32*C2C32×32* C2C32×32为D2的参数矩阵，D2C8×32*C2C32×32为D3的参数矩阵，D2C8×32为D4的参数矩阵。

令C0的参数矩阵为，D1的参数矩阵为，D2的参数矩阵为，D3的参数矩阵为，D4的参数矩阵为，则

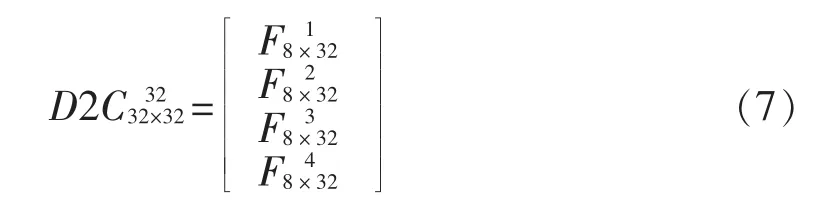
得到当前CRC值与前一级CRC值和当前32位并行数据的关系:

式（8）中D32=[D1，D2，D3，D4]，将式（8）按照式（3）、式（4）、式（5）的方法进行4次迭代计算，得到CRC值与前一级CRC值和当前128位并行数据的关系式为式（9）。

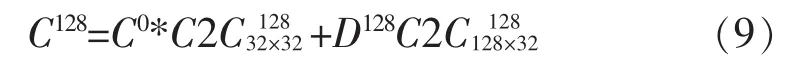
其中，C128为128位并行数据输入后的CRC值，为C0的参数矩阵，D128为128位并行输入数据为128位并行数据的参数矩阵。

2 算法的硬件实现

文中根据第二节的推导公式，基于式（9）提出了一种可以对数据进行预处理的CRC编解码电路[18]。

由式（9）可知，在进行并行128位数据CRC校验时，可以对数据直接进行处理，同时，根据矩阵C2C12832×32对前一级CRC值进行处理，提高了编码效率，大大减少了链路延迟。

如图2所示，文中提出了一种面向128位并行数据的CRC编解码电路。图中的前一级CRC编码模块是以矩阵 D2C128128×32为基本原理转化生成的电路，可以对上一级的CRC值进行编码处理。数据预处理编码模块是以矩阵D2C128128×32为基本原理转化生成的电路模块，对128位并行数据进行预处理编码，并通过逻辑优化实现链路延迟的减少。异或模块对来自前一级CRC编码模块和数据预处理编码模块的数据进行按位异或处理。最终CRC值由反相器输出，校验结果与魔数进行比较，由比较器输出结果。

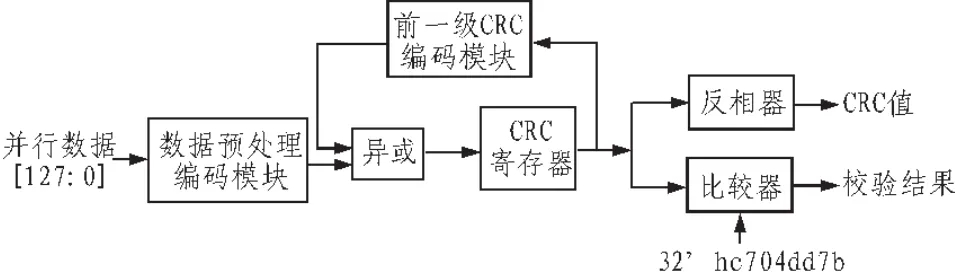
图2 128位并行数据的CRC编解码电路

3 实验验证及分析

为验证文中提出的电路结构的有效性和合理性，使用Modelsim搭建验证环境进行仿真、使用synplify综合工具对电路进行综合。为了进行对比，采用了基于synopsys公司的8位并行数据校验电路对同一组数据进行校验，以对比校验编码的正确性。

仿真结果如图3、图4所示。其中图3为采用文中提出的编码校验电路的功能时序图；图4为基于synopsys公司的8位并行数据校验电路的功能时序图，其输入与图3的输入相同，分为26个时钟周期，每个时钟并行输入8位数据。如图3、图4所示，两种电路所的到的结果一致。

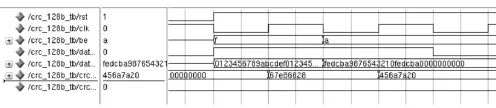
图3 128位并行数据的CRC电路功能时序图

图4 synopsys公司8位并行数据的CRC电路功能时序图

选用Xilinx公司Virtex 5系列的X65VLX330T芯片对本文设计的并行128数据的CRC-32校验电路进行逻辑综合，为了进行比较，针对文献[5]中所提出的基于级联结构的电路进行了布局布线，综合结果见表1。

表1 128位并行数据CRC-32编解码电路综合结果

从表1中可以看出，对于128并行数据的CRC-32编码，文中所述的方法相对于级联结构，由于对组合逻辑链路进行了算法上的优化和结构上的改进，缩短了最长延迟路径，从而在面积仅增加5.15%的情况下，将工作的时钟频率提高了1.8倍[19]。

4 结束语

随着网络通信速率的日渐提高，迫切需要支持宽位并行数据的实时校验电路，文中提出了一种可单周期实现的、面向128位并行数据的循环冗余校验算法。该算法通过对逻辑电路进行优化处理，提高了工作时钟频率，可以实现对128位并行数据的CRC快速编码和解码校验。并且，文中在迭代过程中所涉及到的参数矩阵，在工程应用中均有重要实用价值，可以应用于以太网、PCIe等高速通信网络。

[1]刘新宁.一种快速CRC算法的硬件实现方法[J].电子器件，2003，26（1）:88-91.

[2]Amila，Akagic， Hideharu，et al.A Study of Adaptable Co-processors for Cyclic Redundancy Check on an FPGA[D].Japan:Hiyoshi，2012.

[3]王月琴，杨恒新.CRC码串并结合算法的研究与实现[J].计算机技术与发展，2014，24（6）:103-106.

[4]Kiyana，Bahadori.Multiclass classification of error correcting output[J].Australian Journal of Basic and Applied Sciences，2015，5（9）:538-543.

[5]袁征，冶晓隆，郭超.基于FPGA的10G以太网并行CRC设计 [J].计算机工程与设计，2014，35（5）: 1510-1515.

[6]徐展琦，裴昌幸，董淮南.一种通用多通道并行CRC计算及其实现[J].南京邮电大学学报，2008，28（2）:53-57.

[7]Li C C，Lei Z.CRC codes for short control frames in IEEE 802.11ah[C]//Vehicular Technology Conference（VTC Fall），2014 IEEE 80th.IEEE，2014: 1-5.

[8]Lou C Y.An analytical packet error rate prediction for punctured convolutional codes and an application to CRC code design[J].Dissertations&Theses-Gradworks，2015.

[9]Bartholomew E O，Oscar E A.Error detection in a multi-user request system using enhanced CRC algorithm[J].International Journal of Information Technology&Computer Science，2014，6（9）:14-23.

[10]Deng H，Wang C.Verifi cation of CRC error detecting capability based on monte-carlo simulation[J].Railway Signalling&Communication Engineering，2014.

[11]刘岩俊，闫海霞．HDLC通讯协议中CRC的应用[J]．电子测量技术，2010（3）：21-23．

[12]彭伟．嵌入式系统CRC循环冗余校验算法设计研究[J]．南京信息工程大学学报：自然科学版，2012（3）：258-265．

[13]吕晓敏．嵌套循环冗余码（CRC）的优化与检验[D]．杭州：浙江大学，2012．

[14]莫元劲．并行CRC在FPGA上的实现[J]．电子设计工程，2011（15）：133-135．

[15]杜瑞，张伟功，邓哲，等．新型总线中并行CRC算法的设计与实现[J]．计算机工程与设计，2013（1）：131-135．

[16]肖飞，余子寒，隋天宇，等．LTE中CRC算法的研究与实现[J]．电子测量技术，2014（7）：36-39．

[17]Wu F，Jia S，Meng Q，et al.Improved CRC calculation strategies for 64-bit serial rapidIO[J]. Ieice Transactions on Electronics，2013，E96.C（10）:1330-1338.

[18]朱党杰，孙江辉，蒋学东.RS级联CRC编码在遥测系统中的应用[J].电子科技，2013（7）：40-42.

[19]郝永健,张团善,周文胜,等.动态纱线张力传感器弹簧片的有限元模态分析[J].西安工程大学学报，2015（3）：358-361.

Parallel CRC verification algorithm based on matrix

ZHAO Kun-peng，WU Long-sheng，MA Xu-han，CHEN Qing-yu
（Xi'an Microelectronics Technology Institute，Xi'an 710054，China）

To target the real-time verification requirement of the parallel data in the high speed network communication，the CRC（Cyclic Redundancy Check）algorithm which can implement check of 128-bit parallel data in a single cycle is presented in this paper.Firstly，the CRC check matrix for 8-bit parallel data is extrapolated base on the principle of CRC serial encoding.Then，that check matrix is iteratively simplified to calculate the parameter matrix of 32-bit parallel data.The parameter matrix is regarded as the most significant part in the proposed algorithm and is used to pre-process data.Finally，the algorithm is implemented by hardware.The results of simulation and synthesis show that the encoding and decoding check of 128-bit parallel data can be finished in a single cycle based on the proposed algorithm and the clock frequency increases by 1.8 times with the hardware overheads only increasing 5.15%.

128-bit parallel data；single cycle；CRC algorithm；hardware implementation；frequency increase

TN492

：A

：1674－6236（2017）03-0085-04

2016-01-21稿件编号：201601193

赵坤鹏 （1989—），男，河北石家庄人，硕士研究生。研究方向：以太网ASIC设计。