低信噪比小样本下的短波测向技术

李立峰,冯晓东

(1.装备工程技术研究实验室,河北 石家庄 050081；2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081；3.装备发展部军事代表局驻石家庄地区军事代表室，河北 石家庄050081)

低信噪比小样本下的短波测向技术

李立峰1,2,冯晓东3

(1.装备工程技术研究实验室,河北 石家庄 050081；2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081；3.装备发展部军事代表局驻石家庄地区军事代表室，河北 石家庄050081)

针对短波信道衰落导致接收信噪比低引起测向性能下降的问题，提出了谱线增强技术，利用窗函数对阵元接收信号在测向前进行复指数加权处理，达到提高信噪比的目的。针对传统空间谱测向算法在小样本数或信号源相近等条件下分辨率严重下降的问题，提出了基于谱函数二阶偏导数的处理方法，达到提高测向分辨率的目的。最后对测向性能进行了分析验证，证实了该方法的有效性和适用性。

短波信道；低信噪比；谱线增强；二阶偏导数

0 引言

短波测向[1]存在信号密集度高、接收场强差异大以及示向度游动大等特点，由于短波信道[2]存在着严重的衰落现象，有可能采集到的信号正好达到衰落最低点，达不到测向所需的信噪比要求，导致测向结果出现较大的偏差[3]。传统空间谱测向算法[4]为了能对样本空间更加准确地估计，一般采用比较大的样本数，但是样本数的过分增多会带来计算量大的问题，阵列分辨空间信号的能力与阵列孔径有关，阵列孔径越大，阵列的分辨能力越强。所以，要提高算法的分辨率，就必须增大天线的孔径，但是在实际测向系统中，阵列孔径往往是有限制的，那么如何在阵列孔径一定且信号环境非理想的条件下获得较高的分辨率，是值得研究的问题。

1 提高接收信号信噪比的处理方法

在低信噪比环境下，空间谱测向性能下降[5]。为了提高测向信噪比[6]，可以在测向前对采样信号进行谱线增强[7]的处理，如图1所示。

谱线增强处理就是对每个接收通道的采样信号进行加权的过程，处理过程如下：

① 根据采样信号的信噪比，选择适当的时间窗长度L；

② 产生复指数时间窗函数w：

w=[1,ej2πf0Ts,ej2πf02Ts,……,ej2πf0(L-1)Ts]，

式中，Ts为采样信号的采样周期；

③ 运用窗函数w对采样信号进行复指数加权处理。

对谱线增强后的数据进行如文献[8-11]所述的非均匀取样，进一步减弱噪声信号间的相关性，从而进一步提高对微弱信号[12]的估计性能。

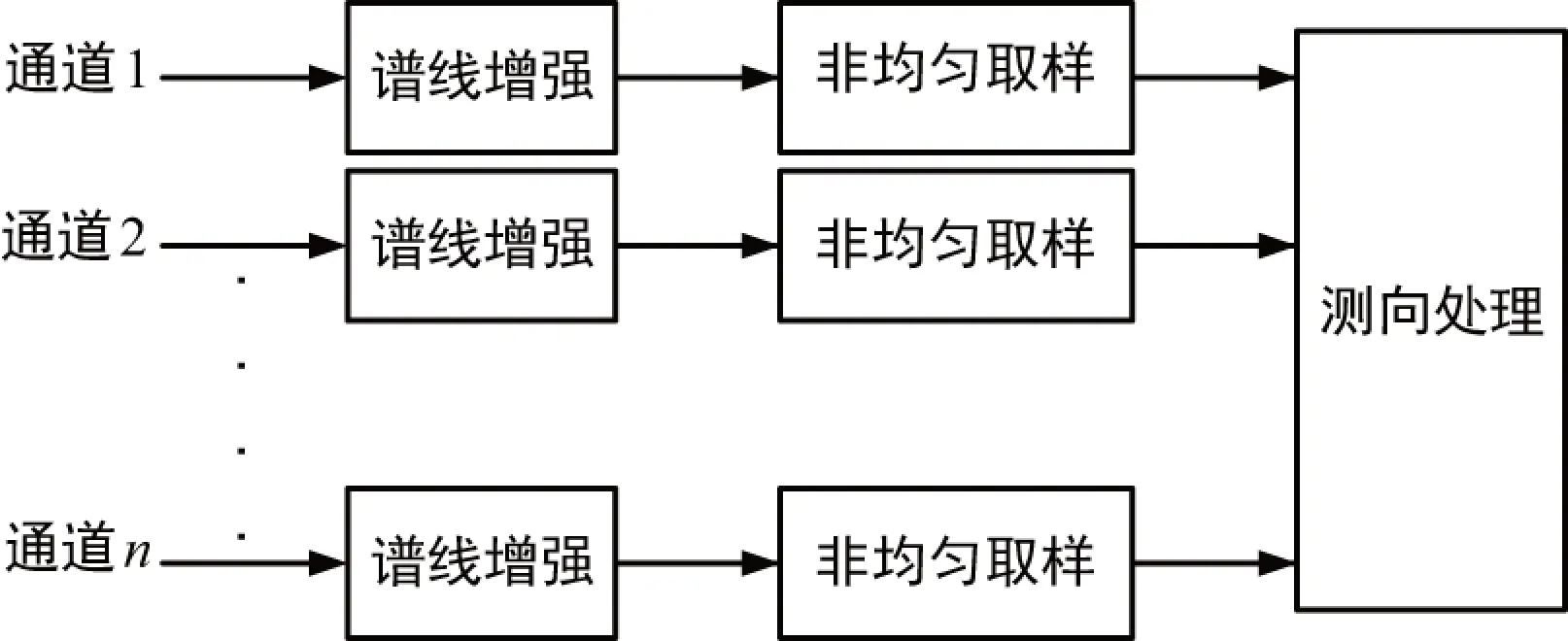
图1 接收信号谱线增强过程

2 基于二阶偏导数的高分辨处理方法

为了提高在低信噪比和小样本数下二维DOA的分辨率和估计性能，提出了一种基于二阶偏导数[13]的二维DOA估计新方法。

假设方位角θ范围为Rθ，搜索间隔为Δθ，仰角φ范围为Rφ，搜索间隔为Δφ，令N=Rθ/Δθ，K=Rφ/Δφ，空间谱函数P可表示[14]为：

由上式可以看出，对于每个给定的坐标(i,j),i=1、2、…、N,j=1、2、…、K，都对应着一个确定的实数pij，设自变量

θ∈D1={θ1,θ2,…,θN},θi+1-θi=Δθ，

φ∈D2={φ1,φ2,…,φK},φj+1-φj=Δφ，

这里当i≠j时，θi与θj互不相同，φi与φj互不相同，则：

pij=f(θi,φj)，

式中，f为二元离散函数。由文献[15]可知，任意二元有限离散函数在其定义域内都存在偏导，且其性质与连续函数的常规偏导数非常相似。因此，在点(θk,φl)处，可得二元有限离散函数p对自变量θ的一阶偏导数为：

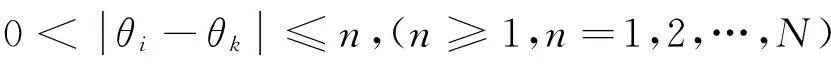
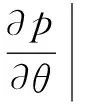
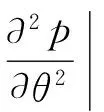
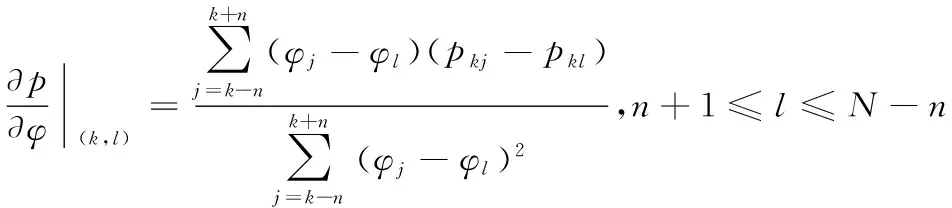
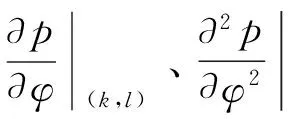
利用MUSIC谱函数极大点对方位角和俯仰角的二阶偏导数都小于零的特性，对空间谱进行负向谱峰搜索可得到目标的DOA。

3 性能分析

① 谱线增强处理对测向性能的影响

8单元均匀圆阵，真实来波方向65°，信号频率10.83 MHz，接收信号信噪比低于5 dB，对谱线增强处理前后的测向性能进行对比。

图2中，横坐标表示方向，单位为(°)，纵坐标表示合成增益，单位dB。黑实线表示谱线增强后的波束图，波束指向64°，黑虚线表示谱线增强前的波束图，波束指向60°。从试验结果可以看出，谱线增强后空间谱图变得很尖锐，测向分辨率得到明显提高，测向结果更加接近真实方位。

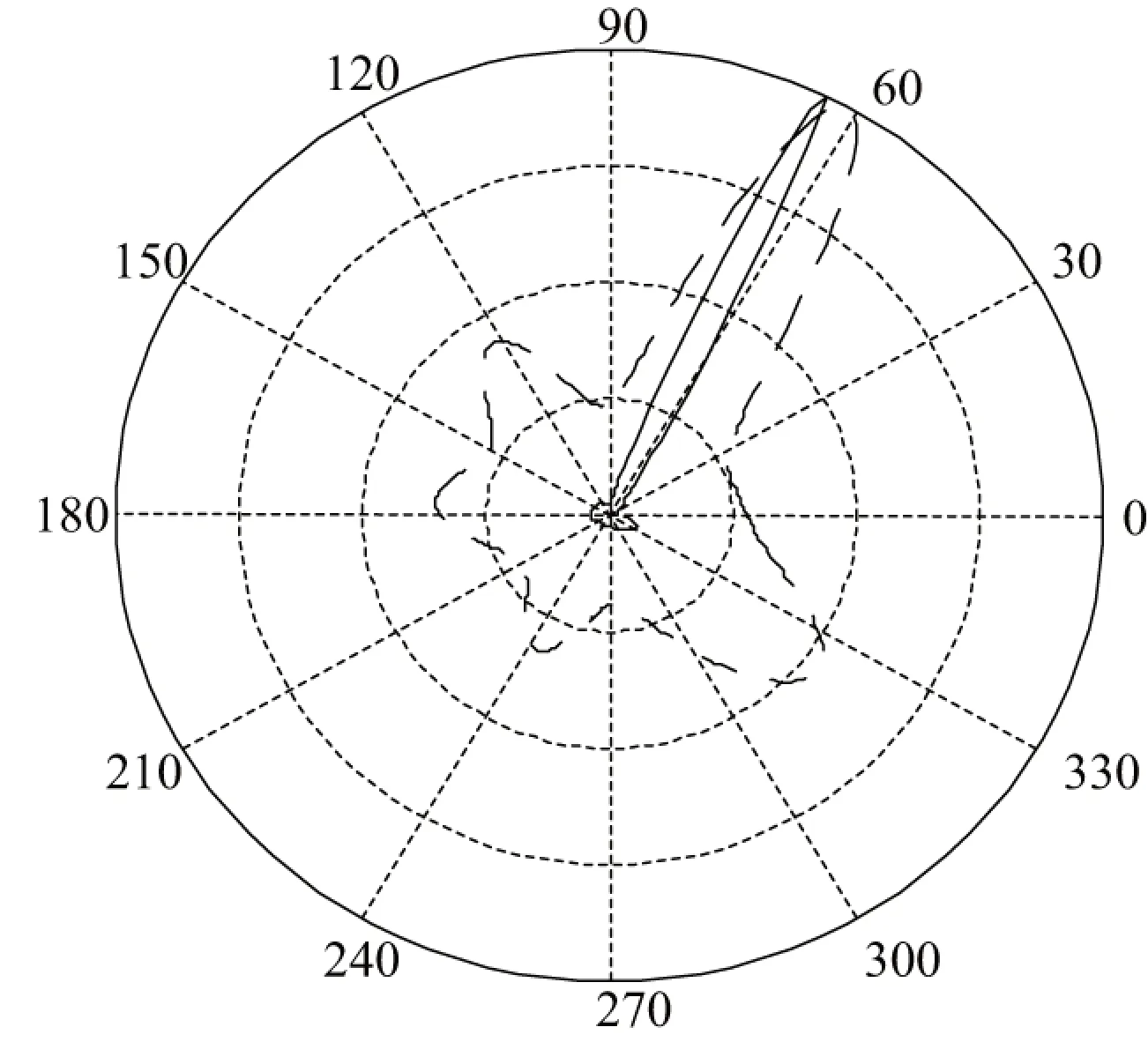
图2 谱线增强处理前后的测向对比

② 谱函数二阶导数处理对测向性能的影响

8单元均匀圆阵，真实来波方向65°，信号频率10.83 MHz，样本点数100，对谱函数二阶导数处理前后的测向性能进行对比。

图3中，横坐标表示测向次数，纵坐标表示测向结果，单位为(°)。黑Ο线表示谱二阶导数处理后的测向结果，测向结果都在65°附近，黑*线表示谱二阶导数处理前的测向结果，相对于真值浮动较大。从试验结果可以看出，经过对谱函数作二阶偏导数处理后，出现较大偏差的概率大大减小，测向精度、测向分辨率有所提高。

图3 谱函数二阶导数处理前后的测向结果对比

③ 联合处理对测向性能的影响

综合利用以上2种处理方法，对处理前后的测向性能进行对比。

图4中，横坐标表示方向，单位为(°)，纵坐标表示合成增益，单位dB。黑实线表示联合处理后的波束图，波束指向64°，黑虚线表示谱线增强后的波束图，波束指向64°，黑点划线表示谱线增强前的波束图，波束指向68°。从试验结果可以看出，通过谱线增强和对谱函数二阶导数处理后，可以在波达方向附近形成更加尖锐的谱峰，测向精度和分辨率具有明显的提高。

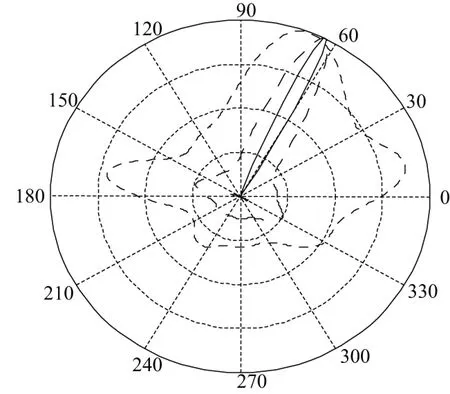
图4 联合处理前后的测向对比

4 结束语

本文通过谱线增强技术有效地提高了接收信号的信噪比，解决了短波信道的衰落导致接收信号太弱而不能正确测向的技术难题，明显提高了测向精度和稳定性。通过对谱函数求二阶偏导数处理，有效解决了小样本条件下测向分辨率低的问题，可以明显提高测向分辨率和测向精度。综合2种处理方法，可以同时提高低信噪比、小样本数下的测向精度和分辨率。新方法在短波侦测系统中得以应用，在天波试验中得到了充分的验证。

[1] Rubsaman M,Gershman A B.Direction-of-arrival Estimation for Non Uniform Sensor Arrays：from Manifold Separation to Fourier Domain MUSIC Methods[J].IEEE Trans on Signal Processing,2009,57(2)：588-599.

[2] Watterson C C,Juroshek J,Bensema W.Experim Ental Confirmation of an HF Channel Model[J].IEEE Trans.Commun Technol,1970,18(6)：792-803.

[3] 涂旭东.宽带短波信道特性和建模研究[D].成都：电子科技大学，2004.

[4] Schmidt R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Trans.on Antennas and Propagation,1986,34(3)：276-280.

[5] 蔡臻祥，马义德，李红领.多径效应对测向精度试验的影响[J].无线电工程，2006，36(2)：37-39.

[6] 潘玉平，齐青茂.波束形成技术在短波侦测中的应用[J].无线电工程，2007，37(5)：33-34.

[7] 刘辉涛，丛卫华，潘 翔.窄带弱信号的线谱检测[J].浙江大学学报，2007，41(12)：2048-2051.

[8] 李 安，王 殊，屈晓旭，等.基于非均匀采样的空时级联频率和到达角估计[J].系统工程与电子技术，2010，32(3)：478-482.

[9]LeeJY，GreengardL.TheType3NonuniformFFTandItsApplications[J].JournalofComputationalPhysics，2005，206(1)：1-5.

[10]KubatJA，ChouJJ，RovnyakD.NonuniformSamplingandMaximumEntropyReconstructionAppliedtotheAccurateMeasurementofResidualDipolarCouplings[J].JournalofMagneticResonance，2007，186(2)：201-211.

[11]LiuYJ，MengHD，WangDS，etal.AdaptiveStaggeringTimeEstimationforTargetTrackinginPeriodicNonuniformSamplingSystem[J].ElectronicsLetters，2007，43(24)：1385-1387.

[12] 张家平，刘 青.低信噪比中MUSIC算法研究[J].通信技术，2009，42(1)：87-89.

[13] 司伟建，蓝晓宇.提高空间谱算法分辨率的DOA估计[J].应用科学学报，2013，31(4)：382-386.

[14] 刘 剑，于红旗.基于二阶预处理的共轭扩展MUSIC算法[J].系统工程与电子技术，2008，30(1)：57-60.

[15] 王文丽.有限离散函数的导数和性质[J].大学数学，2006，21(3)：110 -113.

HF DOA Technique under Low SNR and Small Number of Snapshots

LI li-feng1,2，FENG Xiao-dong3

(1.Equipment Engineering Technology Research Laboratory,Shijiazhuang Hebei 050081,China;2.The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China;3.Military Representative Office of Equipment Development Department in Shijiazhuang,Shijiazhuang Hebei 050081,China)

The performance of DOA decreases under low signal noise ratio(SNR) because of shortwave channel fading.In view of this problem,a method named spectral-line enhancement algorithm is proposed.In order to improve SNR,the array arriving data is processed by complex-exponential weighting using window function before DOA.The resolution decreases in direction of arrival(DOA) estimation under severe environments such as small number of snapshots or incident waves from close angles.In view of this problem,a high-resolution estimation method is proposed based on calculation of the second derivative of spectrum.Finally,the test results show that this method is available and applicable.

shortwave channel;low SNR;spectral-line enhancement;second derivative

10.3969/j.issn.1003-3114.2017.02.11

李立峰,冯晓东.低信噪比小样本下的短波测向技术[J].无线电通信技术,2017,43(2)：44-46,54.

2016-11-02

国家部委基金资助项目

李立峰(1977—)，男，高级工程师，主要研究方向：通信对抗、阵列信号处理。冯晓东(1977—)，男，工程师，主要研究方向：通信工程、通信信号处理。

TN911

A

1003-3114(2017)02-44-3