基于Wasserstein距离和分裂Bregman方法的图像分割算法

王 瑜，闫 沫

（1.西安航空学院 机械工程学院，陕西西安710077；2.西安建筑科技大学机电工程学院，陕西西安710055）

基于Wasserstein距离和分裂Bregman方法的图像分割算法

王 瑜1，闫 沫2

（1.西安航空学院 机械工程学院，陕西西安710077；2.西安建筑科技大学机电工程学院，陕西西安710055）

针对基于C-V模型的活动轮廓分割算法无法应用于灰度非均匀图像分割的问题。采用Wasserstein距离作为区域直方图相似性测度，提出基于该测度的非参数活动轮廓分割模型。在模型求解时引入全局凸分割和分裂Bregman方法，减少了计算量。大量实验结果表明该模型不依赖初始轮廓曲线的位置，能够对灰度非均匀图像进行较准确的分割，具有较快的运算速度。

图像分割；Wasserstein距离；分裂Bregman方法；全局凸分割；活动轮廓

图像分割是图像处理和计算机视觉领域的基本问题。基于变分公式的活动轮廓模型（active contour model，ACM）是近年来最有成效的一类算法。该类算法通过对嵌入区域及其边界特征描述的能量泛函最小化完成对图像区域的划分[1]。

目前常见的活动轮廓模型主要分为两大类：基于边界的模型[2-5]和基于区域的模型[6-8]。最常见的基于边界的活动轮廓模型被称为测地活动轮廓模型[3]（Geodesic Active Contour，GAC）。它使用图像梯度构建边缘停止函数 （edge stopping function，ESF）使曲线演化停止在目标边界。对于弱边缘或梯度噪声大的图像来说，该算法难以得到理想的分割结果。

针对这一问题，Chan和Vese[6]提出著名的基于区域的分割模型，即C-V模型。C-V模型能在既没有明显边界，也缺乏明显纹理特征的图像中分割目标和背景。Chan等人最初提出的C-V模型为了保持曲线演化的稳定性，需要在曲线演化过程中周期性的进行水平集函数重新初始化操作，使其保持符号距离函数（signed distance function，SDF）的性质。因此传统C-V模型的计算量较大。为了避免水平集函数的重新初始化、提高算法的运算速度，Li等人[5]提出在原始能量泛函中增加新的约束项大大提高了算法的运算速度。最近，Zhang等人[9]提出新的基于区域的ACM模型，该模型采用SBGFRLS（Selective Binary and Gaussian Filtering Regularized Level Set）方法，使用二值函数作为水平集函数并利用高斯核函数对其正则化，有效避免水平集演化过程中的重新初始化操作，相对于Li等人的算法，其运算速度得到进一步的提高[10]。与此同时，该算法同时结合了上述两类模型的优点使其具有更好的分割效果和更快的运算速度。

由于上述算法是一种参数区域模型。模型以同质区域作为假设条件，因此在面对灰度复杂的图像时，无法获得较好的分割效果。非参数活动轮廓模型利用像素概率密度分布或局部直方图来分割图像。文献[8-12]采用了Wasserstein距离作为区域相似性测度，取得了较好的分割效果，然而计算量较大使该算法在实践中难以应用。另一方面，活动轮廓模型图像的分割效果一般依赖于初始曲线的位置，不当的初始轮廓会导致分割结果进入局部解。文献[13]在图像分割问题中采用了分裂Bregman技术得到了全局最优解，并且得到了快速解。然而该算法仍然是基于C-V模型，因此仍然具有C-V模型本身的特点。

文中以Wasserstein距离作为区域相似性测度，结合全局凸分割和分裂Bregman方法，提出新的基于全局最优的分割算法。该算法不依赖于初始曲线位置，与前面的算法相比具有较强的鲁棒性和较快的运算速度。

1 基于Wasserstein距离的活动轮廓模型

1.1 Wasserstein距离

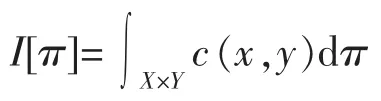
1.2 模型定义

板涧河调蓄水库主要建筑物，包括大坝、溢洪道、导流泄洪洞、连通洞及补水泵站。大坝为2级建筑物，溢洪道和泄洪洞为3级建筑物，补水泵站为2级建筑物。洪水标准为50年一遇设计，1 000年一遇校核。

令Ω为R2上的有界开子集，I:Ω→[0，L]为给定灰度图像。假设活动C曲线将图像划分为内部区域Cin和Cout外部区域。对每一像素点x∈Ω，定义其局部直方图为：

其中，r为邻域半径，|·|为集合的势，Nx，r是以为半径的的邻域，表示像素灰度。

分割模型的能量函数可以定义为：

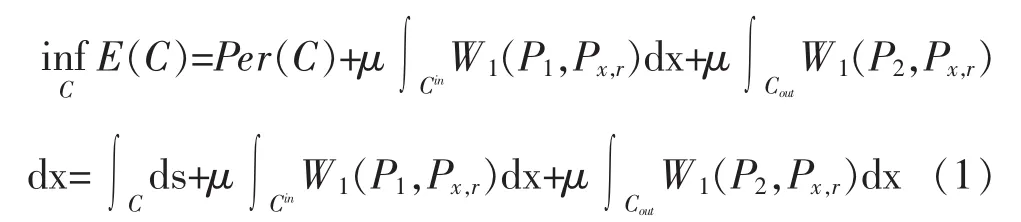
其中Per（C）表示曲线C的长度，P1、P2分别表示活动曲线内外区域直方图。根据变分水平集方法[14]，（1）式的曲线演化方程可以写成：

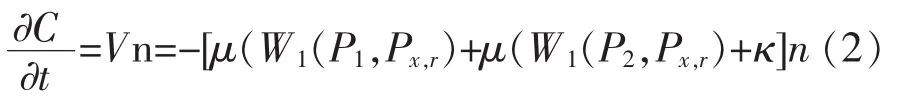
与之相应的零水平集演化方程如下：

2 分割模型的分裂Bregman算法实现

文献[13]在图像分割中首次采用了全局凸分割方法和分裂Bregman技术，该方法针对正则函数提出一种高效的迭代策略从而快速获得全局最小解。首先根据文献[15]，式（3）的稳态解同下式保持一致。

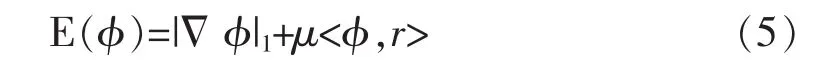
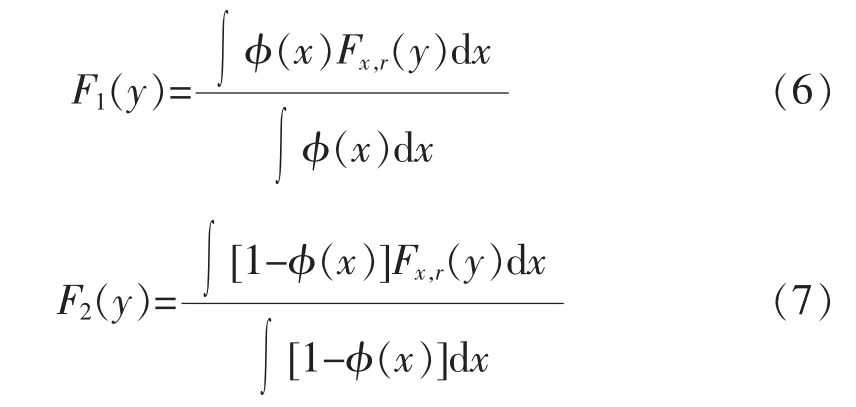
由于式（5）不存在唯一的全局最小解。我们将φ限制在一个有限区间[a，b]内，上式具有全局最小解，可以表示如下：

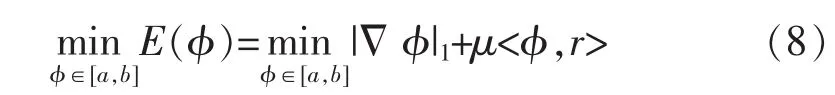
一旦找到φ，可以通过对水平集函数取某个门限α∈（a，b）得到分割区域，如下：

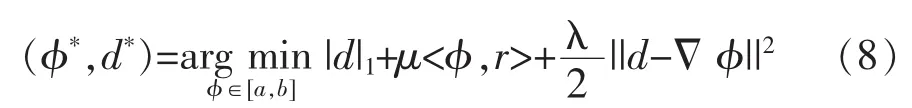
水平集函数φ的求解可以通过采用Bregman迭代进行交替求解。

针对水平集函数φ，对式（9）应用欧拉-拉格朗日公式可以得到：

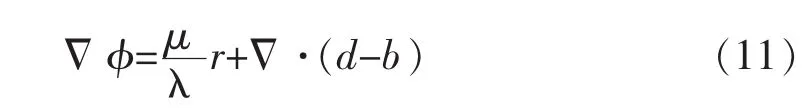
式（11）的数值实现如下：

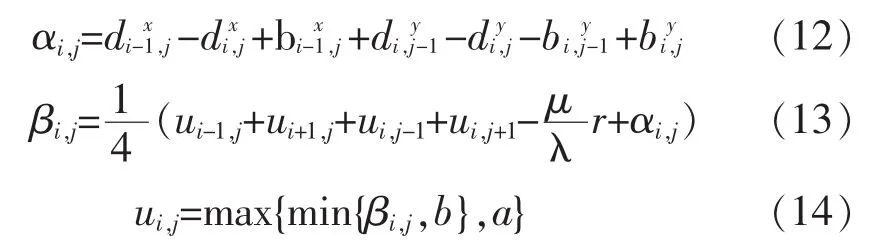
固定φ不变，式（9）相对变量d的最小化可以由下式计算：

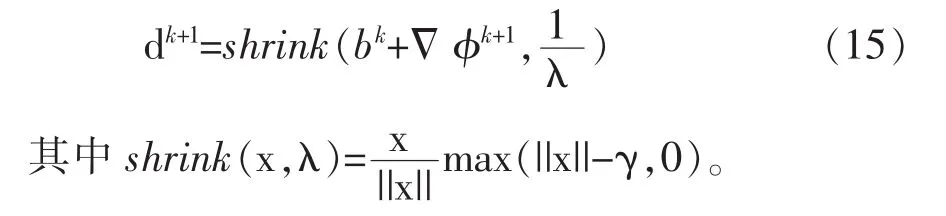
3 实验结果

为了验证算法的有效性，本文针对合成图像和真实图像进行实验。试验中选取参数a=0，b=1，α= 0.5。参数r根据不同的图像进行选择，一般取2≤r≤5。实验结果如下：

图1针对无序特征合成图像进行分割实验。实验结果可以看出，由于采用Wasserstein距离作为区域相似性测度，文献[8]和本文算法获得了较好的分割结果。文献[9]无法获得满意分割，由于本文算法基于全局最优解，因此相对文献[8]分割效果更好。图2针对添加标准差为σ=0.2高斯白噪声的狭长凹陷区域合成图像进行实验。由于凹陷区域过于狭长，传统基于边缘和区域的模型无法给出满意结果。文献[9]结合了GAC模型和C-V模型的优势，其最终轮廓能够进入狭长凹陷区域从而获得满意的分割结果。文献[8]在面对狭长凹陷区域时，算法陷入局部极小值，无法获得满意的分割结果。图3采用同一幅原始图像合成单视SAR强度图像，其数据满足分布。文献[9]由于算法本身针对满足高斯分布的数据，因此虽然在实验二中获得了好的分割结果，但面对SAR图像数据，无法取得满意的分割效果。本文算法基于全局最优解，在实验二和实验三中获得了满意的分割效果。图4、图5分别为真实的医学超声图像和SAR水域图像。实验结果可以看出文献[8]和本文算法获得了较好的分割效果，由于图像内部亮度不均匀，文献[9]无法获得满意的结果。

图1 无序特征图像分割结果

表1 给出了在相同的软硬件条件下（Core2 2.4 GHz CPU，2.00 G RAM，MATLAB平台）文中算法与文献[8-9]算法在运算速度方面的比较结果。从表 1中可以看到，文中算法在获得较好分割效果的同时具有更快的运算速度。

图2 狭长凹陷区域图像（添加高斯噪声）分割结果

图3 狭长凹陷区域图像（单视SAR强度图像）分割结果

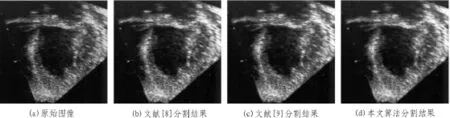
图4 医学图像分割结果

图5 SAR图像水域分割结果

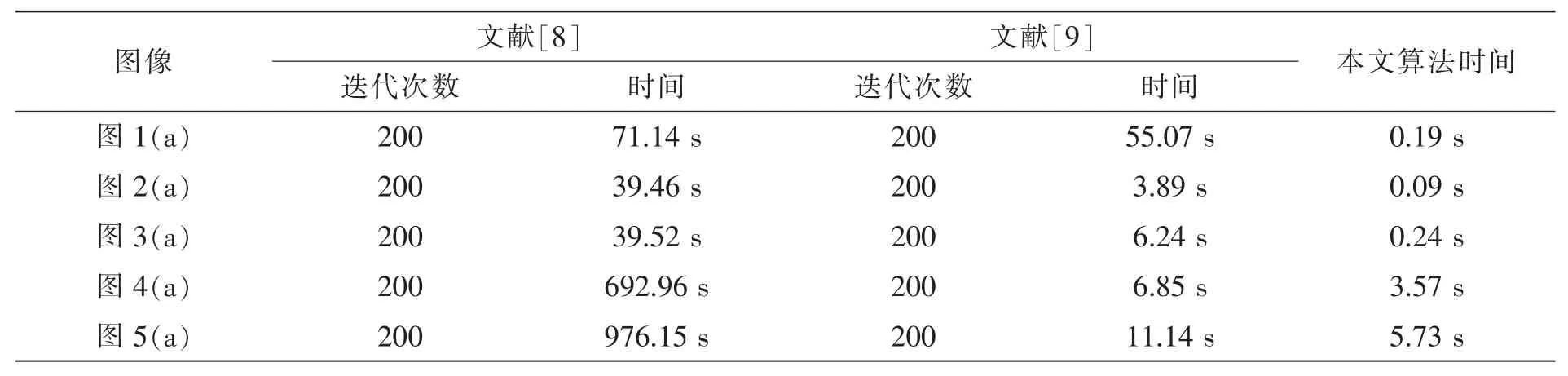
表1 实验中算法运行时间比较

4 结 论

文中利用Wasserstein距离作为区域直方图相似性测度，在基于Wasserstein距离的非参数活动轮廓分割模型基础上引入全局凸分割和分裂Bregman方法。实验结果表明，全局凸分割能够利用图像全局信息获得全局最优解；分裂Bregman方法具有快速收敛的特性。与此同时，传统活动轮廓算法分割结果依赖于初始轮廓的位置，不当的初始轮廓会导致活动轮廓曲线收敛到局部最优解。本文结合了非参数模型的优势和全局凸分割的全局最优解以及分裂Bregman方法的快速收敛特性。实验结果表明，本文算法能够获得较好的分割效果，同时具有较快的运算速度。目前该算法只针对目标和背景两区域图像分割，在已有算法的基础上研究多区域图像分割将是本文后续的重要研究内容之一。

[1]Mumford D，Shah J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Comm.Pure Appl.Math，1989（42）:577-685.

[2]Kass M，Witkin A，Terzopoulos D.Snakes:active contour models[C].International Journal of Computer Vision，1988，1（4）:321-331.

[3]Caselles V，Kimmel R，Sapiro G.Geodesic active contours[C].International Journal of Computer Vision，1997，22（1）:61-79.

[4]Xu C，Prince J L.Snakes，shapes，and gradient vector flow[J].IEEE Trans.On Image Processing，1998（7）:359-369.

[5]Li C M，Xu C Y，Gui C F，et al.Level set evolution without re-initialization:a new variational formulation [C].IEEE Conference on Computer Vision and Pattern Recognition，San Diego，2005: 430-436.

[6]Chan T，Vese L.Active contours without edges[J]. IEEE Trans.On Image Processing，2001，10（2）: 266-277.

[7]Lie J，Lysaker M，Tai X C.A binary level set model and some application to Munford-Shah image segmentation[J].IEEE Transaction on Image Processing，2006（15）:1171-1181.

[8]孔丁科，汪国昭.基于EMD的快速活动轮廓图像分割算法 [J].电子与信息学报，2010，32（5）：1094-1099.

[9]Zhang K H，Zhang L，Song H H，et al.Active contours with selective local or global segmentation:A new formulation and level set method[J].Image and Vision Computing，2010（28）:668-676.

[10]Zhang K H，Song H H，Zhang L.Active contours driven by local image fitting energy[J].Pattern Recognition，2010，43:1199-1206.

[11]ChanT，Esedoglu S，Ni K Y.Histogram based segmentation using Wasserstein distance[C].Scale Space and VariationalMethodsin Computer Vision，Berlin:Springer-Verlag，2007:697-708.

[12]钱晓华，郭树旭，李雪妍，等.基于Wasserstein距离的局部能量分割模型[J].电子学报，2010，38（6）：1-5.

[13]GoldsteinT，Bresson X，OsherS.Geometric Applications ofthe SplitBregman Method: Segmentation and Surface Reconstruction[C].J. Sci.Comput.，2010（45）:272-293.

[14]Amar Mitiche，Ismail Ben Ayed.Varational and Level Set Methods in Image Segmentation[M]. Springer，2010.

[15]Chan T，Esedoglu S，Nikolova M.Algorithms for finding global minimizers of image segmentation and denoising models[J].SIAM J.Appl.Math.，2006（66）:1932-1648.

Image segmentation based on Wasserstein distance and split Bregman method

WANG Yu1，YAN Mo2
（1.School of Mechanical Engineering，Xi'an Aeronautical University，Xi'an 710077，China；2.College of Mechanical and Electrical Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China）

Active contours segmentation algorithms based on C-V model can not be used for intensity non-homogeneity images segmentation.Wasserstein distance is employed as the region histogram similarity measure.A non-parametric active contour model based on this measure is proposed in this paper.Global convex segmentation and split Bregman method is applied to solving the model.It can reduce the amount of computation.Experimental results show that the model does not depend on initial curve.It can segment intensity non-homogeneity images correctly and efficiently.

image segmentation；wasserstein distance；split bregman method；global convex segmentation；active contour

TP 301.6

：A

：1674-6236（2017）02-0140-05

2016-01-04稿件编号：201601006

王瑜（1981—），女，江苏徐州人，硕士，讲师。研究方向：机电一体化、模式识别与目标检测。