一种基于TDOA的弹着点定位改进算法

娄京生，何 为，张 帅，王营冠

（中国科学院 上海微系统与信息技术研究所，上海201800）

一种基于TDOA的弹着点定位改进算法

娄京生，何 为，张 帅，王营冠

（中国科学院 上海微系统与信息技术研究所，上海201800）

针对传统炮弹定位算法精度不高，实时性较差的缺点，提出一种基于TDOA的改进定位算法，并通过靶场实地数据对算法加以检验。该算法适用于传感器间连线成任意角度的阵列，并结合KMeans算法剔除离群点保证数据质量。实地数据检验表明，该算法明显提高了定位精度，并且规避了解高阶方程组带来的繁冗计算，达到了预期目标。

数据预处理；TDOA；夹角-射线算法；K-Means算法

炮弹命中率是炮弹发射技术中相当重要的指标。准确及时地掌握弹着点位置，对于校正发炮参数，提高打击精度非常必要。目前，武器装备不断发展进步，先进的武器对目标测量，参数校正的要求也越来越高，但国内相应的测试设备却相对落后，无法满足信息化装备的测试要求。

由于缺乏较为精确的的定位系统设备，目前，我国炮弹炸点定位仍以人工检测为主[1]。对于地面炮弹炸点坐标的测量，采用爆炸后找弹坑插标杆的原始测量方式法；对于空中炸点坐标的测量，则采用观察爆炸光的光学交汇法[2]。人工观察测量效率低下且存在漏检现象和安全隐患，光学交汇较人工检测稍安全，但是CD摄像设备造价昂贵，并且指挥镜交汇也可能漏捕或者丢失数据。在我们国内，以信号检测为基础的被动声源、振动源定位系统的研究起步比较晚，南京理工大学、北京理工大学、中北大学与工程兵技术装备研究所等都在这方面进行过论证、实验和研究[3]。

目前运用被动传感器阵列进行定位的算法主要有三大类：DOA、TOA、TDOA[4]基于无线传感器网络的炮弹落点定位技术的研究。DOA法在平面定位中易受到角度分辨率、多径效应和噪声等的干扰；TOA算法的定位精度与信号到达时间点的测定，有十分紧密的联系，并且对各个传感器通道响应的时间同步性要求十分苛刻[5]，很小的误差对实验结果也会造成较大影响；TDOA法规避了波速的测量，利用不同传感器间的接收到信号的时间差实现定位，该方法可以抵消相同干扰因素对信号造成的时间误差，是一种应用广泛的目标定位技术[6]。因此，文中采取TDOA定位算法为基础进行定位，并且提出了一种基于TDOA的改进算法。

1 TDOA定位算法原理

传统意义上，TDOA定位原理的实质就是双曲线的性质[7]。一般假定到达不同传感器的振动波速度一致，故不同传感器相对于振动源的距离差正比于接收到信号的时间差，进而两个检测点的时间差可以确定一条以这两个监测点为焦点双曲线，振动源也在该双曲线一支上。如果利用三个检测点就可以确定两条双曲线，并且能够得到两个双曲线的交点，信号源必定是双曲线的交点[8]。

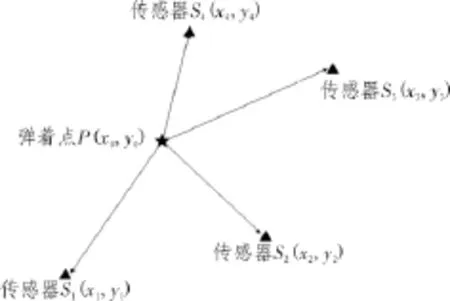
图1 TDOA定位算法示意图

如图1所示，炮弹落点为P，传感器节点分别为设振动波到达1，2，3号传感器的时刻分别为T1，T2，T3，且振动波在这三条路径的传播速度为v，则有[9]：

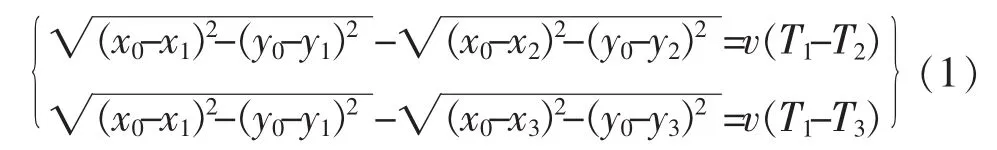
这里，振动波从P点（x0，y0）发出，波面是一簇同心圆。上边两方程，左右两边都是传感器相对于振动源的波达路径差——左边是用传感器、振动源的绝对坐标表示，右边用速度乘以时间表示。解方程组，可得P点坐标（x0，y0）。实际检测中，可以用远多于3个的传感器做检测，进而得到多个交点，进而消除偶然误差[10]。

容易看到，传统的TDOA往往需要解多个高次方程组，计算量很大。尤其是多传感器多交点的情况，还容易产生多组解，甚至虚数解。如何规避高次方程组带来的大计算量（对应实时性）以及对定位结果进行有效筛选（对应精度），是本文要解决的问题。另外传统的定位阵列多为线性布设，我们要尝试分析传感器之间连线成任意角度的情况。

2 数据预处理

2.1 数据截取

文中实验数据采集于6月份山西某靶场实弹演练现场。原始数据量较大，有27G之多，绝大部分时间记录的是传感器噪声，且没有时间戳。准确分离出各次炮弹对应振动数据，才能方便数据处理。数据截取主要采取以下步骤：

图2 Python截取数据步骤

截取后的振动数据如图3所示。可以看出，炮弹落地爆炸引发的振动波多尖脉冲，和噪声有明显的差异。

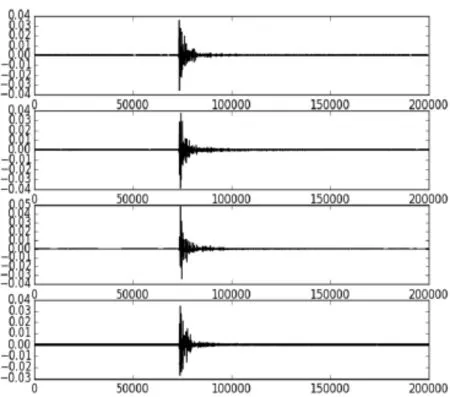
图3 振动数据与噪声数据对比

2.2TDOA计算

无论是应用传统的TDOA定位算法定位，还是用我们改进的算法，都首先要对已截取的数据计算tdoa。

首先做出假设：各个传感器所接收到的振动信号是同一信号——弹着点爆炸所引起的振动，经过不同的延迟得到。那么对截取到的任意两个传感器信号序列作互相关运算，根据互相关函数峰值即可对tdoa估值[11]。

针对一次发炮振动，设任意两个传感器接收到的信号序列分别为Si（k）和Sj（k），其相对相移为lij，那么这两个信号对应的tdoa参数为：

而信号序列Si（k）和Sj（k）的互相关函数为：

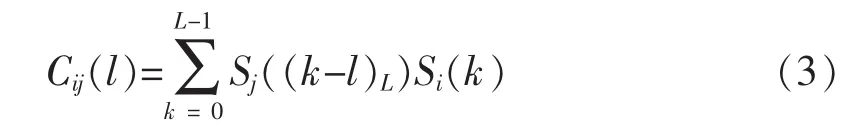
其中，Ts为采样点间隔（已知参数）。L为截取序列的长度，利用式（3）可以求出Cij（l）（l=1，2，…，L-1）的峰值，再结合式（2）可得 tdoa值。以第3发炮弹对应的振动信号为例，选取传感器节点1的信号为基准，其他各点序列相对于该序列的tdoa如表1：

表1 第3发炮弹对应tdoa值

3 夹角-射线算法原理及定位结果

3.1 改进算法原理

该算法基本思想：利用阵列中传感器的几何位置，经过数学公式变换和解三角形，将求落地点与参考点连线与传感器阵列连线夹角转换成求各个传感器对应tdoa差值，然后求比值，反解三角函数得两个角度，从而引出两条射线，交点即为落点。

3.1.1 传感器间连线成直角情况

从最简单的直角情况开始讨论。如图4，A，B，C为传感器阵列的3个节点，其几何位置满足AC⊥BC，且各自位置均可精确测出。右上角O点表示炮弹落点，炮弹在此处爆炸引发振动，而波达路径即OA，OB，OC。∠OCB，即θC，是波达路径OC和传感器节点连线BC方向的夹角，θA和θB同理。如果求得θC，即可知道炮弹落点相对于传感器C的方向（C坐标和BC连线方程已知），即弹着点O必落在以C为端点，与BC连线夹角为θC的射线CO上，记作α。类似地，再选取另一个基准点，作出另一条射线β（图4中未画出），α与β相交即可得到弹着点 O[12]。

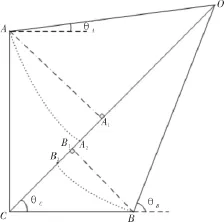
图4 传感器间连线成直角情况

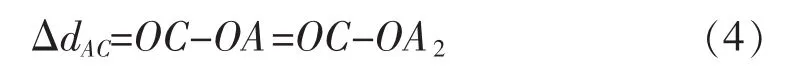
之后，自A点向路径OC作垂线交OC于A1点。用OA1近似代替OA2，此时公式（4）可近似为：

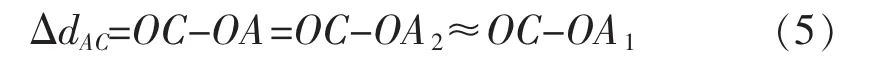
假设波速为v，则波达路径的路程差正比于传感器接收到信号的时间差：

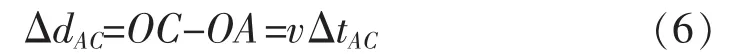
联立（6），可得：

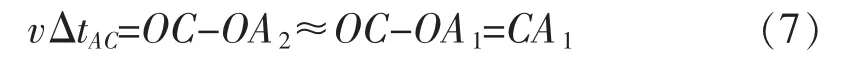
我们注意到，在ΔAA1C中，有：

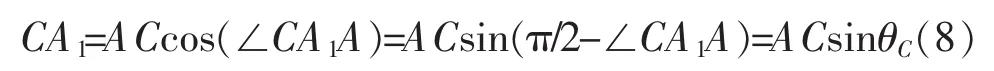
联立（7），可得：

同理，有：

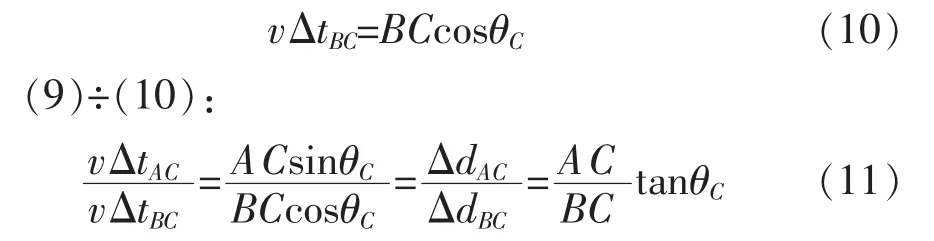
其中，ΔtAC和ΔtBC，即为tdoa，可以用最大似然估计法求出，而AC，BC长度可由全站仪精确测得，故tanθC可得。反解三角函数，夹角θC可得，进而射线OC方程可得。类似地，选取其它基准点，做出对应的射线，与OC相交即可得弹着点O的位置。

这里要单独说明一下，式（5）中用到的近似是忽略A1A2了的长度。之后的计算可验证，这一近似是可行的，因为A1A2长度被验证不超过5 cm，远小于百米以上OA1。

4.根据串联、并联电路电流的特点，判断流过各分电阻的电流变化。根据串、并联电路的特点，即：串联电路中，电流处处相等；在并联电路中，总电流等于各分电流之和。以此为依据来判断流过各分电阻的电流变化。

3.1.2 弹着点落在夹角外部情况

十字阵列中，传感器连线夹角成直角，解三角形较为简单。传感器连线夹角为钝角或者锐角的情况稍微复杂，但只要炮弹落点在∠ACB内部，原理即近似。这里我们要讨论炮弹落点不在∠ACB内部的情况，同时设定传感器间连线成任意角度。如图5所示。

仍然记∠ACB为θC0，∠ACA1为 θC2，∠BCB1为θC1，显然有θC2+θC1=π-θC0。

此时仍有：

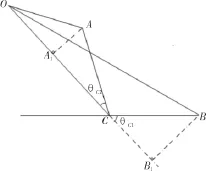
图5 弹着点落在角的外部情况

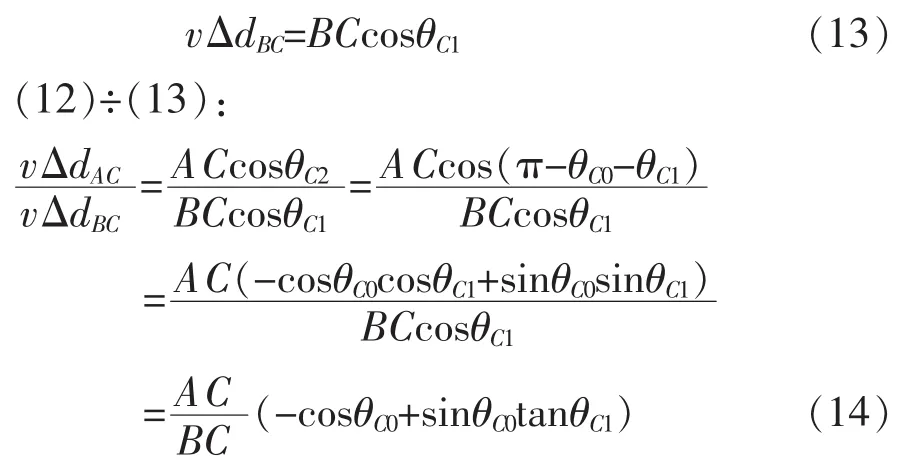
同样地，最终结果中，θC0已知，AC和BC已知，ΔdAC和ΔdBC可求出，反解三角函数可得，射线CO和传感器连线BC夹角为π-θC1。类似地，只要有3个传感器点（其相对位置可任意），我们就可以运用解三角形的方法，求夹角，引射线，进而得出交点。

3.2 K-Means聚类优化结果

文中实验数据采集于6月份山西某靶场实弹演练现场。共发射哑弹1发，实弹5发。传感器阵列分为东、西两个，各包含8路传感器，主要采用高地传感器阵列定位（图6）。

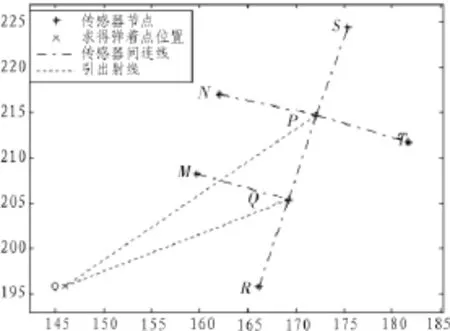
图6 射线交叉定位弹着点

对于每一次发炮弹着点定位，按照3.1中方法，引射线，求交点。实际上，每次可以的夹角-射线交叉（如图6所示虚线），得到8个交点。用K-means剔除初始结果中的离群点，然后取平均（直接取算术平均值或者非线性最小二乘法取平均），即为落点坐标。

值得一提的是，运用K-Means聚类[13]，剔除离群数据可能不止运用一次[14]。以第三发炮弹的落点横坐标为例：

Step 1

针对初始结果——8个交点横坐标K-Means聚类，聚类结果如表2：

可以看到，6个元素值落在了Clister1-1（表示第1轮聚类中的类别1）中，2个元素落到了Clister1-2中。Clister1-1元素个数为优势多数，故将Clister1-2中元素舍弃，只对Clister1-1中元素进行下一轮KMeans聚类。

Step 2

对在Step 1得到的Clister1-1中元素进行KMeans聚类，结果如表3：

表2 第1轮K-Means聚类结果

表3 第2轮K-Means聚类结果

此时，Clister2-1和Clister2-2各包含3个元素，不存在优势多数聚类，故两聚类中所有元素都不能舍弃，此时终止继续聚类，将第2、3、5、6、7、8号交点的横坐标作算术平均 （或者非线性最小二乘法求平均），得到第1发炮弹最终定位横坐标113.49 m，这与真实测量值110.56 m差距很小。

3.3 最终定位结果

表4列出了传统TDOA算法 （需要解高阶方程组）定位结果以及夹角-射线算法的定位结果。表5则对两种算法的定位误差作了比较。可以看出，改进后的算法对定位精度有明显提升。另外，在定位计算中，发现炮弹砸地和爆炸各自引起的振动信号存在混叠，目前在尝试用小波方法将两种信号分离[15]。

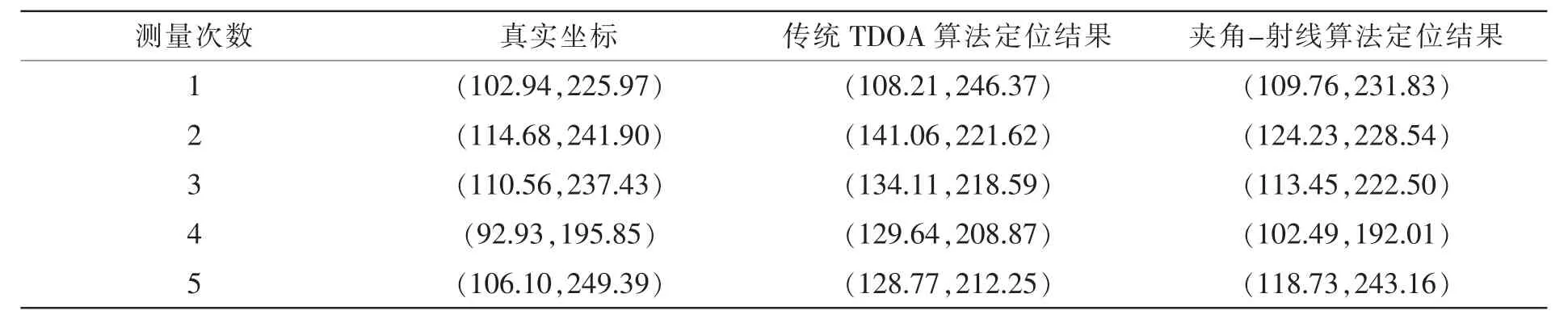
表4 最终定位结果

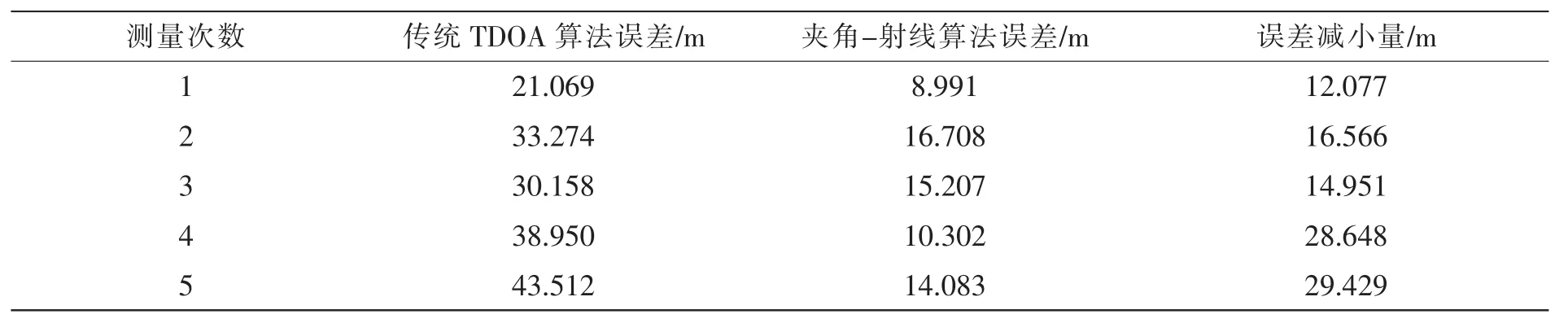
表5 改进算法和传统算法比较

4 结 论

文中讨论了结合TDOA的炮弹落点定位算法。对经典的算法加以改进，提出了针对任意布设方式的夹角-射线定位算法。通过靶场实地数据验证，该算法有效提高了弹着点的定位精度，同时规避了高次方程组求解。改进后的算法符合对定位精度和实时性要求较高的应用场景。

[1]张洪喆，王福豹，段渭军.基于WSN的炮弹着地点定位系统的研究[J].现代电子技术，2011，34（7）: 16-18.

[2]国蓉，何镇安，王伟.被动声探测技术与弹着点定位方法综述[J].电声基础，2010，34（11）:48-52.

[3]刘玉鹏.爆炸炸点传感器特测系统的研究 [D].南京:南京理工工大学，2004:2-3，6-9.

[4]Nafchi，A.R.Univ.of New Mexico，Albuquerque, NM， USA Shu Ting Goh；Reza Zekavat,S.A. Circular Arrays and Inertial Measurement Unit for DOA/TOA/TDOA-Based Endoscopy Capsule Localization:Performance and Complexity Investigation [J].IEEE Sensors Journal （Impact Factor:1.76）. 2014，14（11）:3791-3799.

[5]孔雁，关咏梅，郭 涛，等.基于无线传感器网络的炮弹落点定位技术的研究 [J].传感技术学报，2015，28（8）:1201-1206.

[6]任克强，庄放望.移动锚节点凸规则定位算法研究及改进[J].传感技术学报，2014，10（27）:1406-1411.

[7]丁学文，龚晓峰，武瑞娟.TDOA测向定位相关算法的研究[J].现代电子技术，2009，1:7-10.

[8]Wo，S.Q.，So，H.C，Ching，P.C.Improvement of TDOA measurement using wavelet denoising with a novel thresholding technique[J].IEEE Acoustic, Speech and Signal Processing，1997:539-542.

[9]俞一鸣，姚远，程学虎.TDOA定位技术和实际应用简介[J].中国无线电，2013（11）:57-58.

[10]黄晓利，王福豹，段渭军，等.无线传感器网络TDOA测距误差分析与校正 [J].计算机测量与控制，2008，16（7）:1053-1056.

[11]马金明.TDOA参数估计算法[J].北京邮电大学学报，2007，30（1）:96-99.

[12]赵春晖，李 刚，唐爱华.五元十字交叉阵的测向模糊分析及阵列改进措施[J].应用科技，2006，33（2）:1-3.

[13]李飞，薛彬，黄亚楼.初始中心优化的K—Means聚类算法[J].计算机科学，2002，29（7）:94-96.

[14]EM Knorr，RT Ng，V Tucakov.Distance-based outliers:algorithms and applications[J].Vldb Journalthe International Journal on Very Large Data Bases.2000，8（3-4）:237-253.

[15]Y Yu，Q Jiang，Z Cao.Industrial Signal Filter Base onWavelet Transform[C]//International Conference on Computational Intelligence&Software Engineering，2009:1-4.

Research on an improved algorithm based on TDOA for the location of cannonball impact points

LOU Jing-sheng，HE Wei，ZHANG Shuai，WANG Ying-guan
（Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，Shanghai 201800，China）

The conventional TDOA algorithm for the location of cannonball impact points suffers from low precision and poor efficiency.To overcome these shortcomings，we propose in this paper a new TDOA-based algorithm which is applicable to sensor arrays of random layout.Then K-Means algorithm is also adopted to eliminate outliers and ensure data quality.The experiment and application on data from range show that this algorithm can improve the precision of location and helps to avoid the computational complexity caused by high-order equations.

data preprocessing；TDOA；angle-ray algorithm；K-Means

TN98

：A

：1674-6236（2017）02-0125-05

2016-01-22稿件编号：201601209

娄京生（1990—），男，河南南阳人，硕士研究生。研究方向：数据挖掘，传感器信号处理。